圆周角
图片预览



文档简介
(共20张PPT)
中学数学CAI课件---九年级第28章
圆 周 角
西宁市第十中学 孙仁道
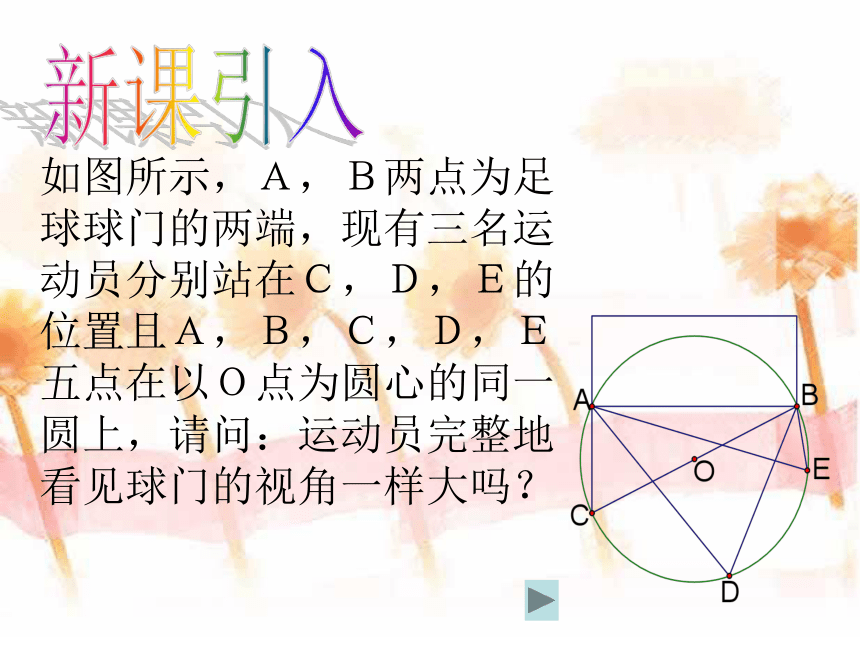
如图所示,A,B两点为足球球门的两端,现有三名运动员分别站在C,D,E的位置且A,B,C,D,E五点在以O点为圆心的同一圆上,请问:运动员完整地看见球门的视角一样大吗?
学习目标
知识目标
方法与情感目标
1.理解圆周角的概念,掌握圆周角的质;
2.能够准确地运用圆周角的性质进行简单的说明计算;
1.通过观察、思考实验探索等活动,分情况说明圆周角定理。了解由特殊到一般的数学思想方法和分类讨论的思想方法。
2.在活动中获取成功的体验,提高学习数学的兴趣。
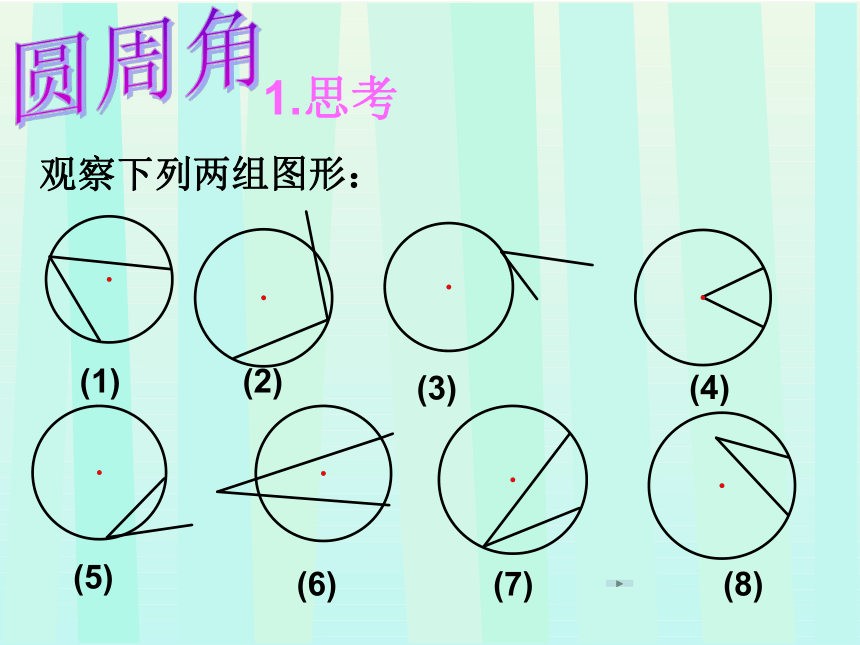
1.思考
观察下列两组图形:
(1)
(2)
(3)
(4)
(5)
(6)
(7)
(8)
以上八个图中的哪些图形中的角的顶点和两边有共同的特征?
(顶点都在圆上,两边是圆的弦。)
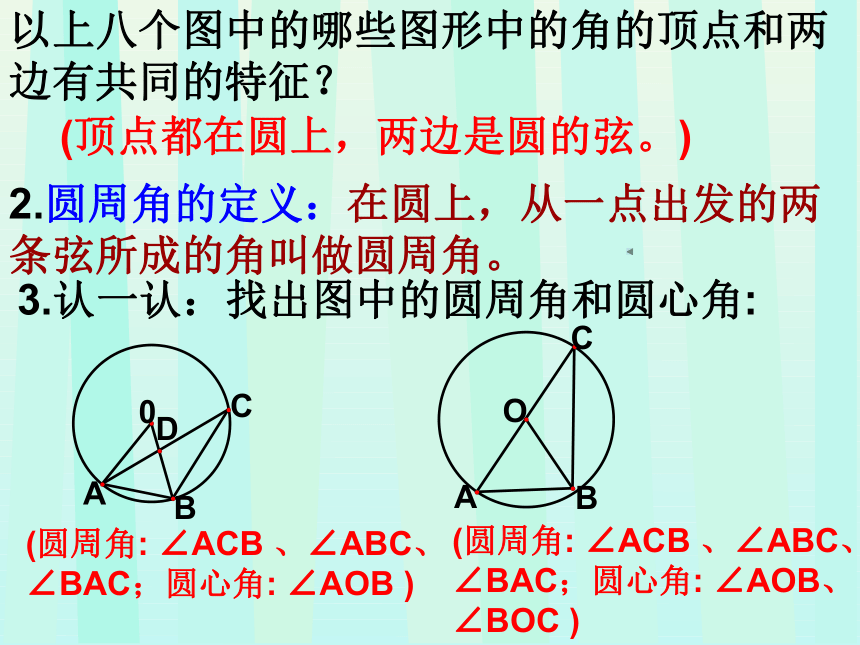
2.圆周角的定义:在圆上,从一点出发的两条弦所成的角叫做圆周角。
3.认一认:找出图中的圆周角和圆心角:
(圆周角: ∠ACB 、∠ABC、∠BAC;圆心角: ∠AOB )
(圆周角: ∠ACB 、∠ABC、∠BAC;圆心角: ∠AOB、∠BOC )
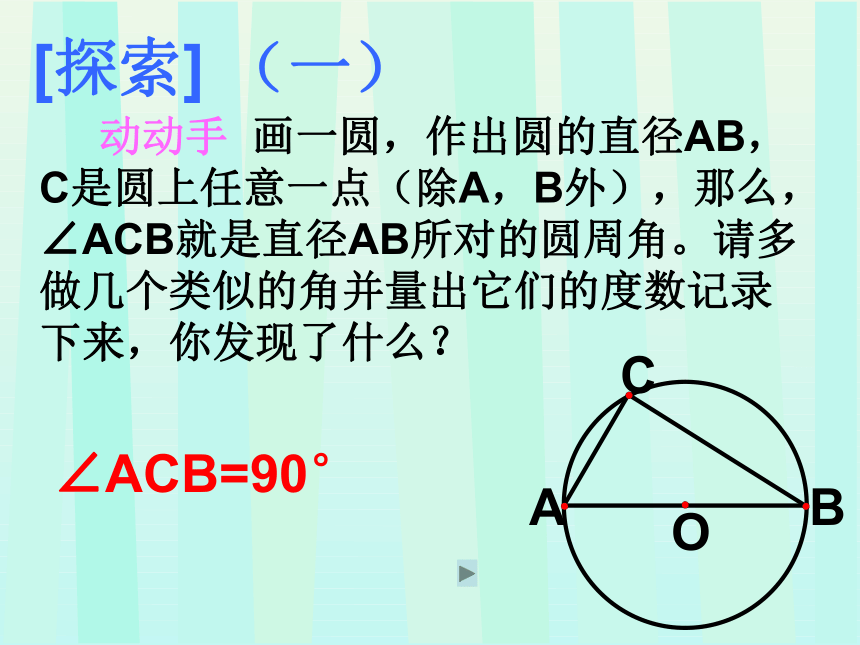
[探索] (一)
动动手 画一圆,作出圆的直径AB,C是圆上任意一点(除A,B外),那么,∠ACB就是直径AB所对的圆周角。请多做几个类似的角并量出它们的度数记录下来,你发现了什么?
∠ACB=90°
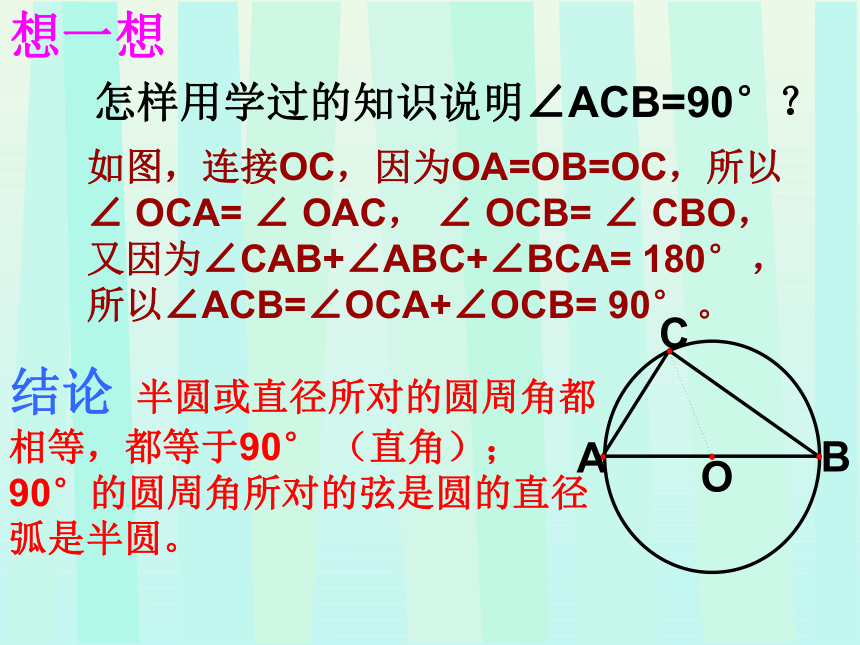
想一想
怎样用学过的知识说明∠ACB=90°?
如图,连接OC,因为OA=OB=OC,所以∠ OCA= ∠ OAC, ∠ OCB= ∠ CBO,又因为∠CAB+∠ABC+∠BCA= 180° ,所以∠ACB=∠OCA+∠OCB= 90° 。
结论 半圆或直径所对的圆周角都相等,都等于90° (直角); 90°的圆周角所对的弦是圆的直径弧是半圆。
用一用
1. AB是⊙O的直径,∠A=80°.求∠ABC的度数.
解 因为AB是⊙O的直径,而直径所对的圆周角是直角,所以
∠ABC=180°-∠A-∠ACB
=180°-80°-90°=10°.
2.你能找到圆形零件的圆心吗?
[探索](二)
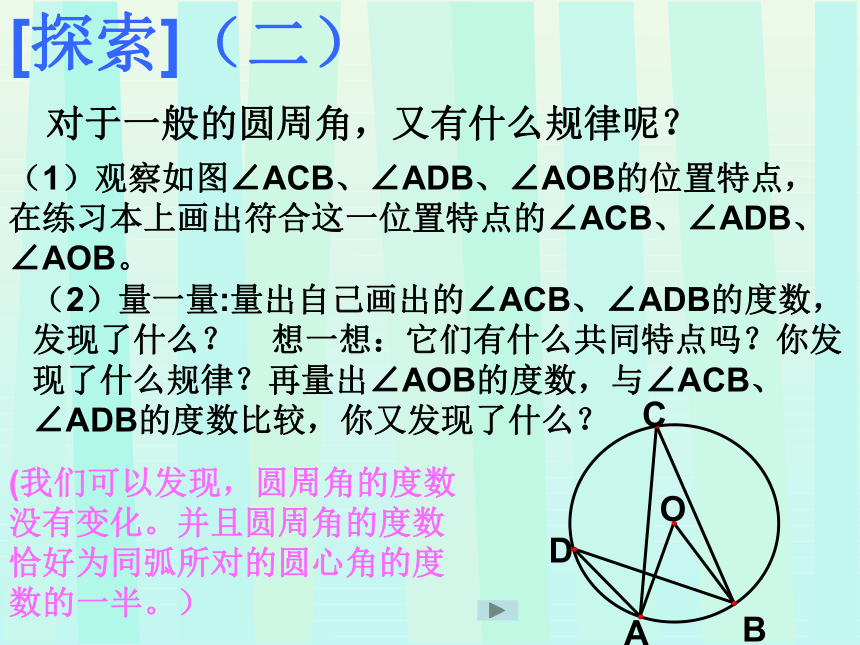
对于一般的圆周角,又有什么规律呢?
(1)观察如图∠ACB、∠ADB、∠AOB的位置特点,在练习本上画出符合这一位置特点的∠ACB、∠ADB、∠AOB。
(2)量一量:量出自己画出的∠ACB、∠ADB的度数,发现了什么? 想一想:它们有什么共同特点吗?你发现了什么规律?再量出∠AOB的度数,与∠ACB、∠ADB的度数比较,你又发现了什么?
(我们可以发现,圆周角的度数没有变化。并且圆周角的度数恰好为同弧所对的圆心角的度数的一半。)
(3)猜想:在一个圆中,一条弧所对的任意一个圆周角的大小都等于该弧所对的圆心角的一半。
(4)如何说明我们猜想的正确性呢?
根据圆周角与圆心的位置关系,归纳起来却只有三中情况即:圆心在角的边上,圆心在角的内部,圆心在角的外部。)如图
o
指导分析:
学生思考:能否把②、③转化为①的情况呢?
分析得出:只要作出直径AD,将∠BAC转化为上述情况的两角之和或两角之差即可。
①如果圆心O在∠BAC的一边AC上,只要利用三角形内角和定理的推论和等腰三角形的性质即可说明。
②如果圆心O在∠ACB的内部,我们怎样说明猜想的结论成立呢
③如果圆心O在∠ ACB的内部,我们怎样说明猜想的结论成立呢
过程说明:
1)当圆心O在∠ACB的内部时,过点A作直径AD,因为
∠CAB=∠CAD+∠BAD,∠CAD= ∠COD,
∠BAD= ∠BOD,所以∠CAB= (∠COD+∠BOD)
= ∠COB,即∠CAB= ∠COB。
过程说明:
2)圆心O在∠ACB的外部时,过点A作直径AD,因为
∠DAC= ∠DOC,∠DAB= ∠DOB,又因为
∠BAC=∠DAC-∠DAB, ∠BOC=∠DOC-∠DOB,所以,
∠BAC= ∠DOC- ∠DOB= ( ∠DOC-∠DOB)=
∠BOC, 即∠BAC= ∠BOC.
结论
一条弧所对的圆周角等于该弧所对的圆心角的一半。
综上所述我们可以知道:在同一圆内,同弧或等弧所对的圆周角相等,都等于该弧所对的圆心角的一半;相等的圆周角所对的弧也相等.
应用迁移,巩固提高
例1求图中角X的度数。
X=35°
X=120°
X=130°
例2已知△ABC中,AB=AC,以AB为直径的圆交BC于D,试说明BD=CD。
解:连结AD
因为AB是直径,所以 ∠ADB=90° ,即AD⊥BC,
又因为AB=AC,所以BD=DC.
巩固练习
1.判断:(1)顶点在圆上的角叫圆周角( )
(2)同弧或等弧所对的圆周角相等( )
(3)相等的圆周角所对的弧也相等( )
(4)直角所对的弦是直径。( )
(5)90°的圆周角所对的弦是直径.( )
2.试找出图中所有相等的圆周角.
∠1=∠4 ,∠2 =∠7,
∠3=∠6 ,∠5=∠8.
3.填空
(1)在圆中圆心角为120 ° ,它所对的弧对的圆周角的度数是( )。
(2)在圆中所对圆周角为40 ° 的弧所对的圆心角的度数是( )。
(3)在圆中,一条弧所对的圆心角和圆周角分别为(2x+100)°和(5x-30)°,则这条弧所对的圆心角度数是( )、圆周角的度数是( ).
总结反思
1.这节课主要学习了两个知识点:
(1)什么是圆周角?
(2)圆周角的性质及其应用。
2.从方法上主要学习了圆周角的性质的说明,渗透了由特殊到一般的数学思想方法和分类讨论的思想方法。
布置作业
教材P52中6题,7题.
谢谢大家
中学数学CAI课件---九年级第28章
圆 周 角
西宁市第十中学 孙仁道
如图所示,A,B两点为足球球门的两端,现有三名运动员分别站在C,D,E的位置且A,B,C,D,E五点在以O点为圆心的同一圆上,请问:运动员完整地看见球门的视角一样大吗?
学习目标
知识目标
方法与情感目标
1.理解圆周角的概念,掌握圆周角的质;
2.能够准确地运用圆周角的性质进行简单的说明计算;
1.通过观察、思考实验探索等活动,分情况说明圆周角定理。了解由特殊到一般的数学思想方法和分类讨论的思想方法。
2.在活动中获取成功的体验,提高学习数学的兴趣。
1.思考
观察下列两组图形:
(1)
(2)
(3)
(4)
(5)
(6)
(7)
(8)
以上八个图中的哪些图形中的角的顶点和两边有共同的特征?
(顶点都在圆上,两边是圆的弦。)
2.圆周角的定义:在圆上,从一点出发的两条弦所成的角叫做圆周角。
3.认一认:找出图中的圆周角和圆心角:
(圆周角: ∠ACB 、∠ABC、∠BAC;圆心角: ∠AOB )
(圆周角: ∠ACB 、∠ABC、∠BAC;圆心角: ∠AOB、∠BOC )
[探索] (一)
动动手 画一圆,作出圆的直径AB,C是圆上任意一点(除A,B外),那么,∠ACB就是直径AB所对的圆周角。请多做几个类似的角并量出它们的度数记录下来,你发现了什么?
∠ACB=90°
想一想
怎样用学过的知识说明∠ACB=90°?
如图,连接OC,因为OA=OB=OC,所以∠ OCA= ∠ OAC, ∠ OCB= ∠ CBO,又因为∠CAB+∠ABC+∠BCA= 180° ,所以∠ACB=∠OCA+∠OCB= 90° 。
结论 半圆或直径所对的圆周角都相等,都等于90° (直角); 90°的圆周角所对的弦是圆的直径弧是半圆。
用一用
1. AB是⊙O的直径,∠A=80°.求∠ABC的度数.
解 因为AB是⊙O的直径,而直径所对的圆周角是直角,所以
∠ABC=180°-∠A-∠ACB
=180°-80°-90°=10°.
2.你能找到圆形零件的圆心吗?
[探索](二)
对于一般的圆周角,又有什么规律呢?
(1)观察如图∠ACB、∠ADB、∠AOB的位置特点,在练习本上画出符合这一位置特点的∠ACB、∠ADB、∠AOB。
(2)量一量:量出自己画出的∠ACB、∠ADB的度数,发现了什么? 想一想:它们有什么共同特点吗?你发现了什么规律?再量出∠AOB的度数,与∠ACB、∠ADB的度数比较,你又发现了什么?
(我们可以发现,圆周角的度数没有变化。并且圆周角的度数恰好为同弧所对的圆心角的度数的一半。)
(3)猜想:在一个圆中,一条弧所对的任意一个圆周角的大小都等于该弧所对的圆心角的一半。
(4)如何说明我们猜想的正确性呢?
根据圆周角与圆心的位置关系,归纳起来却只有三中情况即:圆心在角的边上,圆心在角的内部,圆心在角的外部。)如图
o
指导分析:
学生思考:能否把②、③转化为①的情况呢?
分析得出:只要作出直径AD,将∠BAC转化为上述情况的两角之和或两角之差即可。
①如果圆心O在∠BAC的一边AC上,只要利用三角形内角和定理的推论和等腰三角形的性质即可说明。
②如果圆心O在∠ACB的内部,我们怎样说明猜想的结论成立呢
③如果圆心O在∠ ACB的内部,我们怎样说明猜想的结论成立呢
过程说明:
1)当圆心O在∠ACB的内部时,过点A作直径AD,因为
∠CAB=∠CAD+∠BAD,∠CAD= ∠COD,
∠BAD= ∠BOD,所以∠CAB= (∠COD+∠BOD)
= ∠COB,即∠CAB= ∠COB。
过程说明:
2)圆心O在∠ACB的外部时,过点A作直径AD,因为
∠DAC= ∠DOC,∠DAB= ∠DOB,又因为
∠BAC=∠DAC-∠DAB, ∠BOC=∠DOC-∠DOB,所以,
∠BAC= ∠DOC- ∠DOB= ( ∠DOC-∠DOB)=
∠BOC, 即∠BAC= ∠BOC.
结论
一条弧所对的圆周角等于该弧所对的圆心角的一半。
综上所述我们可以知道:在同一圆内,同弧或等弧所对的圆周角相等,都等于该弧所对的圆心角的一半;相等的圆周角所对的弧也相等.
应用迁移,巩固提高
例1求图中角X的度数。
X=35°
X=120°
X=130°
例2已知△ABC中,AB=AC,以AB为直径的圆交BC于D,试说明BD=CD。
解:连结AD
因为AB是直径,所以 ∠ADB=90° ,即AD⊥BC,
又因为AB=AC,所以BD=DC.
巩固练习
1.判断:(1)顶点在圆上的角叫圆周角( )
(2)同弧或等弧所对的圆周角相等( )
(3)相等的圆周角所对的弧也相等( )
(4)直角所对的弦是直径。( )
(5)90°的圆周角所对的弦是直径.( )
2.试找出图中所有相等的圆周角.
∠1=∠4 ,∠2 =∠7,
∠3=∠6 ,∠5=∠8.
3.填空
(1)在圆中圆心角为120 ° ,它所对的弧对的圆周角的度数是( )。
(2)在圆中所对圆周角为40 ° 的弧所对的圆心角的度数是( )。
(3)在圆中,一条弧所对的圆心角和圆周角分别为(2x+100)°和(5x-30)°,则这条弧所对的圆心角度数是( )、圆周角的度数是( ).
总结反思
1.这节课主要学习了两个知识点:
(1)什么是圆周角?
(2)圆周角的性质及其应用。
2.从方法上主要学习了圆周角的性质的说明,渗透了由特殊到一般的数学思想方法和分类讨论的思想方法。
布置作业
教材P52中6题,7题.
谢谢大家
