勾股定理
图片预览



文档简介
勾股定理
在本章中,我们探索了直角三角形的三边关系,并在此基础上得到了勾股定理,并学习了如何利用拼图验证勾股定理,介绍了勾股定理的用途;本章后半部分学习了勾股定理的逆定是以及它的应用.其知识结构如下:
在学习勾股定理时应注重知识的形成过程,即勾股定理的探索过程,有意识地培养自己探索新知识的能力.在运用勾股定理时一定要有直角三角形这个前提条件,因此,通过有关具体问题时,有时需添加适当的辅助线以构造直角三角形来帮助解题.
勾股定理的逆定理是用来判定一个三角形是否是直角三角形的,但在判定一个三角形是否是直角三角形时应首先确定该三角形的最大边,当其余两边的平方和等于最大边的平方时,该三角形才是直角三角形.勾股定理的逆定理也可用来证明两直线是否垂直,这一点同学们也应牢牢掌握.
典例精讲
例1 如图,有一块直角三角形纸片,两直角边AC=6cm,BC=8cm,现将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AE重合,求CD长.
方法指导:可设CD长为xcm,再寻找等量关系利用方程思想来解,而在直角三角形中,等量关系往往是勾股定理表达式.
解:设CD=xcm,则BD=BC—CD=(8—x)cm.
由题知△ACD与△AED关于AD对称,
∴AE=AC=6cm,DE=CD=xcm,∠AED=∠C=90°.
在Rr△ACB中,由勾股定理得:,
∴BE=AB—AE=10—6=4cm.
在Rt△BED中,由勾股定理得:.
∴,解得x=3cm.
方法总结:折叠问题应把握折叠前后两部分图形关于折痕对称,从而可以利用对称的有关性质来帮助解题目.
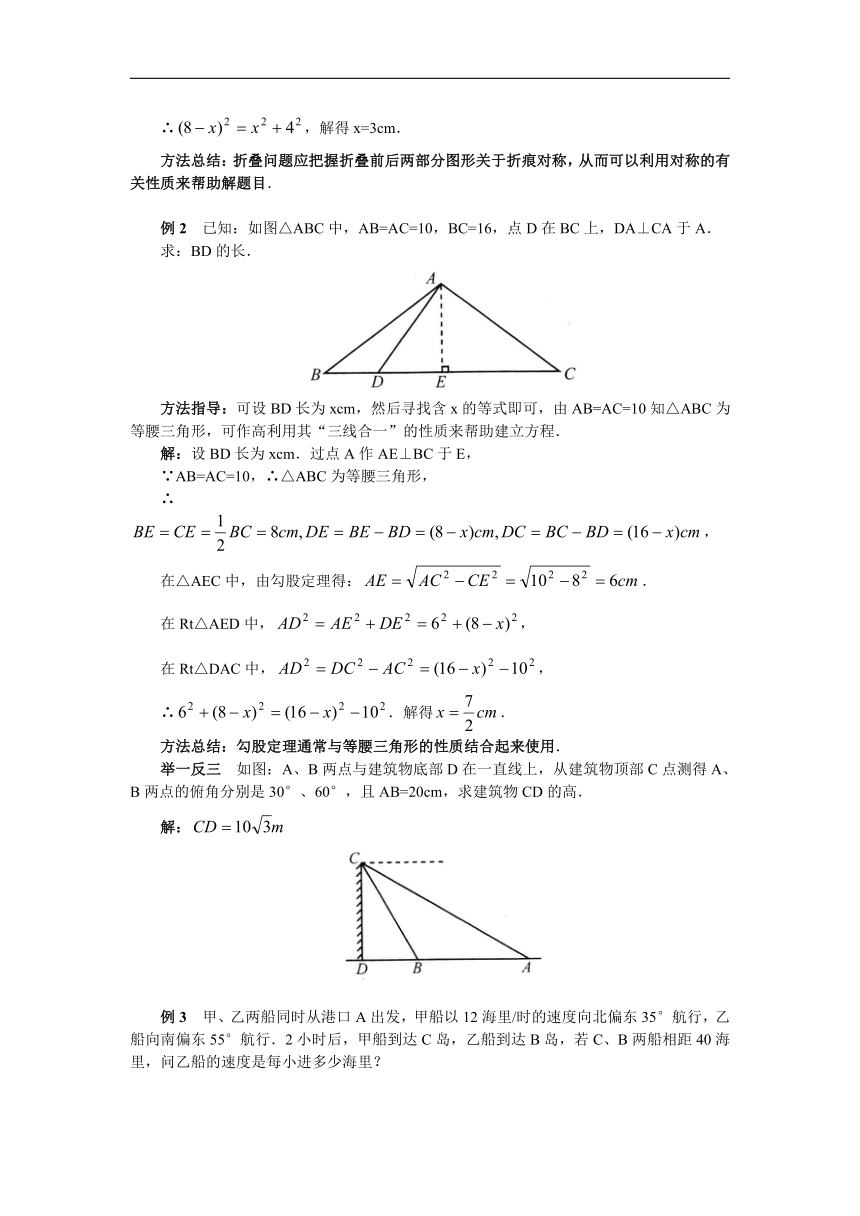
例2 已知:如图△ABC中,AB=AC=10,BC=16,点D在BC上,DA⊥CA于A.
求:BD的长.
方法指导:可设BD长为xcm,然后寻找含x的等式即可,由AB=AC=10知△ABC为等腰三角形,可作高利用其“三线合一”的性质来帮助建立方程.
解:设BD长为xcm.过点A作AE⊥BC于E,
∵AB=AC=10,∴△ABC为等腰三角形,
∴,
在△AEC中,由勾股定理得:.
在Rt△AED中,,
在Rt△DAC中,,
∴.解得.
方法总结:勾股定理通常与等腰三角形的性质结合起来使用.
举一反三 如图:A、B两点与建筑物底部D在一直线上,从建筑物顶部C点测得A、B两点的俯角分别是30°、60°,且AB=20cm,求建筑物CD的高.
解:
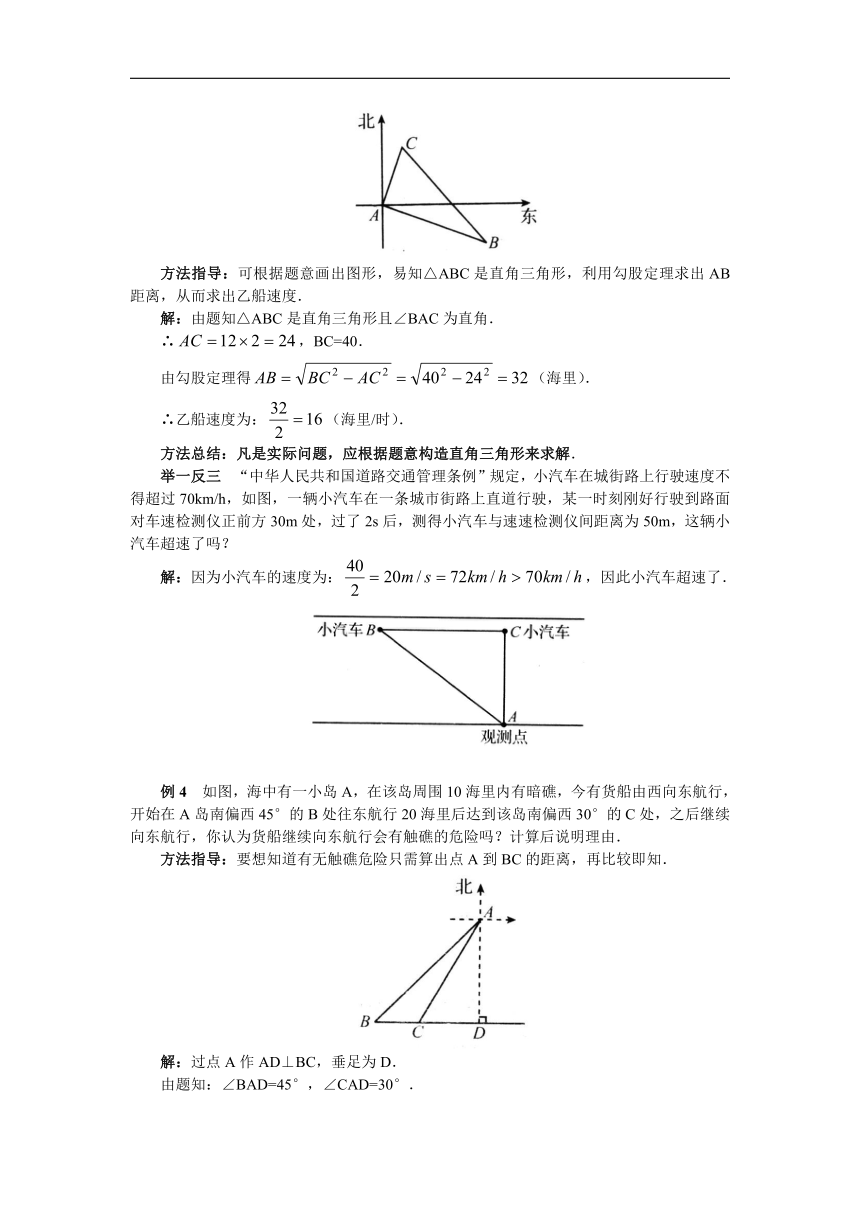
例3 甲、乙两船同时从港口A出发,甲船以12海里/时的速度向北偏东35°航行,乙船向南偏东55°航行.2小时后,甲船到达C岛,乙船到达B岛,若C、B两船相距40海里,问乙船的速度是每小进多少海里?
方法指导:可根据题意画出图形,易知△ABC是直角三角形,利用勾股定理求出AB距离,从而求出乙船速度.
解:由题知△ABC是直角三角形且∠BAC为直角.
∴,BC=40.
由勾股定理得(海里).
∴乙船速度为:(海里/时).
方法总结:凡是实际问题,应根据题意构造直角三角形来求解.
举一反三 “中华人民共和国道路交通管理条例”规定,小汽车在城街路上行驶速度不得超过70km/h,如图,一辆小汽车在一条城市街路上直道行驶,某一时刻刚好行驶到路面对车速检测仪正前方30m处,过了2s后,测得小汽车与速速检测仪间距离为50m,这辆小汽车超速了吗?
解:因为小汽车的速度为:,因此小汽车超速了.
例4 如图,海中有一小岛A,在该岛周围10海里内有暗礁,今有货船由西向东航行,开始在A岛南偏西45°的B处往东航行20海里后达到该岛南偏西30°的C处,之后继续向东航行,你认为货船继续向东航行会有触礁的危险吗?计算后说明理由.
方法指导:要想知道有无触礁危险只需算出点A到BC的距离,再比较即知.
解:过点A作AD⊥BC,垂足为D.
由题知:∠BAD=45°,∠CAD=30°.
设AD=x(海里),则BD=x(海里),CD=(x—20)(海里),
我们知道有一内角为30°的直角三角形三边比值为.
∴,即.
解得.
故无触礁危险.
方法总结:此题若直接用勾股定理也可得关于x的方程,但是是一元二次的,目前无法解出来,故应熟记特殊直角三角形的三边比值,如等腰直角三角形三边比值为.
举一反三 如图,点A是一个半径为300m的圆形森林公园的中心,在森林公园附近有B、C两个村庄,现要在B、C两村庄之间修一条长为1000m的笔直公路将两村连通.经测得∠ABC=45°,∠ACB=30°,问此公路是否会穿过该森林公园?请通过计算进行说明.
解:不会穿过公园.
例5 一架方梯长25m,如图,斜靠在一面墙上,梯子底端离墙7m,求:(1)这个梯子的顶端距地面有多高?(2)如果梯子的顶端下滑了4m,那么梯子的底端在水平方向滑动了几米?
方法指导:梯子靠在墙上即构成直角三角形,可利用勾股定理来求解.
解:(1)如图,在Rt△POQ中,由勾股定理得:
.
即梯子的顶端距离地面24m;
(2)由题知梯子底端移动的距离为OB,
设QB=x,则OA=OP—AP=24—4=20m,
梯子下滑过程中长度不变即AB=QP=25m,
在Rr△AOB中,由勾股定理得:
.
∴QB=OB—OQ=15—7=8m.
即梯子底端移动了8m.
方法总结:这是一类“梯子下滑问题”,解此类题应把握两点:梯子靠在墙上即构成直角三角形;梯子滑动过程中长度不变.
举一反三 如图,一个梯子AB长2.5m,顶端A靠在墙AC上,这时梯子下端B与墙角C距离为1.5m,梯子滑动后停在DE的位置上,测得BD长为0.5m,求梯子顶端A下落了多少m?
解:梯子顶端A下落了0.5m.
例6 若△ABC的三边分别为a、b、c,且满足,那么△ABC是何种形状?
解:由得
,
即,
∴a=3,b=4,c=5.
∵,由勾股定理逆定理知△ABC是直角三角形.
方法总结:要判断三角形形状,应寻找三边关系或三角之间的关系再作出判断.
举一反三 若a、b、c为△ABC的三边,且满足.探索△ABC的形状,并说明理由.
解:等边三角形.
例7 如图,CD是△ABC的AB边上的高,且有.求证:△ABC是直角三角形.
方法指导:先依题意画图,再利用勾股定理的逆定理来证.
解:在Rt△ACD中,由勾股定理得:
.
∴,同理,,
.
由勾股定理逆定理知:△ABC是直角三角形.
方法总结:证明直角三角形或两直线的垂直关系通常用勾股定理逆定理来解决.
举一反三 如图,已知在△ABC中,∠C=90°,D为AC上一点,与 有怎样的关系?试证明你的结论.
解:相等(提示:可证明,再作移项变形.)
本章综合练习
(时间90分钟,满分120分)
一、填空题(3分×10=30分)
1.在△ABC中,∠C=90°,a,b,c为∠A,∠B,∠C的对边.
(1)c=25,b=24,那么a=_________.
(2)a=30,b=16,那么c=_________.
2.在△ABC中,a,b,c为∠A,∠B,∠C的对边.
(1),那么当c=___________时,∠B=90°.
(2),那么当b=____________时,∠C=90°.
3.在△ABC中,∠C=90°,AB=40,AC=24.则斜边AB上的高是__________.
4.在△ABC中,a,b,c为∠A,∠B,∠C的对边,如果a,b,c满足,那么△ABC是以____________为斜边的直角三角形.
5.如图,每个小正方形的边长是1,在图中画出:
(1)一个面积为2的直角三角形.
(2)一个面积为2的正方形.
6.如图,△ABC中,BC=12,AB=10,△ABC的面积是48.那么BD=__________.
7.一个三角形的一个外角等于和它相邻的内角,如果此三角形的两条边长分别是5,2,那么以第三条边为半径的圆的面积是___________(保留).
8.边长为2的正三角形的面积为__________,边长为a的正三角形面积为___________.
9.如果梯子的底端离建筑物9m,那么15m长的梯子可以到达建筑物的高度是_________.
10.为得到湖两岸A点和B点间的距离,一个观测者在C点设桩,使∠ABC为直角(如图),并测得AC长20m、BC长16m,A,B两点间的距离是_________.
二、选择题(7分×3=21分)
11.有下列命题:
(1)如果a,b,c为一组勾股数,那么4a,4b,4c仍是勾股数;
(2)如果直角三角形的两边长是3,4,那么斜边必是5;
(3)如果一个三角形的三边是12,25,21,那么此三角形必是直角三角形;
(4)一个等腰直角三角形的三边长为a,b,c(a>b>c),那么.其中正确的是( )
A.(1)(2) B.(1)(3) C.(1)(4) D.(2)(4)
12.如图,△ABC中,AB=AC,AD⊥BC,垂足是D,AB=13,BD=5,则△ABC的面积是( )
A.65 B.120 C.60 D.36
13.如图,△ABC中,∠ACB=90°,AC=BC,如果△ABC的面积是8,那么腰长是( )
A.4 B.2 C.8 D.16
14.如图,B在A的北偏西α方向的6m处,C在A的北偏东β方向的8m处,并且,那么B、C两点相距( )
A.6m B.8m C.10m D.12m
15.如图,在Rt△ABC中,∠C=90°,D为AC上的一点,且有DA=DB=5,又△DAB的面积是10,那么DC的长是( )
A.4 B.3 C.5 D.4.5
16.在△ABC中,AB=AC,如果AB=17,BC=16,则BC边上的中线长是( )
A.8 B.15 C.10 D.6
17.如图,在Rt△ABC中,∠B=90°.以AC为直径的圆恰好过点B.AB=8,BC=6,则阴影部分的面积是( )
A. B.
C. D.
三、阅读理解题(5分)
18.阅读下列解题过程,并回答问题.
已知a,b,c为△ABC的三边,且满足,试判定△ABC的形状.
解:∵, ①
∴. ②
∴, ③
∴△ABC是直角三角形.
(1)上述解题过程,从哪一步开始出现错误?请写出代号___________.
(2)错误的原因为__________.
(3)本题正确结论为____________.
四、解答题(64分)
19.(8分)下面同学对各题的解答是否正确?为什么?
(1)在Rt△ABC中,∠B=90°,a=3,b=4,求c;
(2)已知直角三角形两条直角边为40和9,求第三边的长;
(3)已知△ABC中,AB=10,AC=17,BC边上的高AD=8,求BC的长.
解:(1)由勾股定理得:
,
∴.
(2)由勾股定理得:
,
∴,
∴c=41,
答:第三边的长为41.
(3)根据勾股定理:
,∴DB=8;
,∴DC=15.
故BC=15+8=24.
20.(8分)有一个三角形两边长分别为4和5,要使三角形为直角三角形,则第三边为多少?
21.(8分)给出一组式子:.
(1)你能发现关于上式中的一些规律吗?
(2)请你运用所发现的规律,给出第5个式子.
(3)请你证明你所发现的规律.
22.(8分)在△ABC中,已知a=15,b=17,c=8,求△ABC的面积.
23.(8分)如图,在△ABC中,∠ACB=90°,CD⊥AB,D为垂足,DE⊥BC,E为垂足,已知AC=6,AB=10.
求(1)CD的长;(2)DE的长.
24.(8分)如图,△ABC中,AD⊥BC,D为垂足,AE为BC边上的中线,已知AB=5,BC=12,△ABC的面积是24.
求(1)AD的长;
(2)判断△ABE的形状,并说明理由.
25.(8分)如图,在△ABC中,∠ACB=90°,CD为AB边上的高.试说明.
26.(8分)如图,在△ABC中,AM是BC边的中线,AE为BC边上的高.试判断与的关系,并说明理由.
参 考 答 案
1.(1)7 (2)34 2.(1)1 (2)3 3.19.2 4.a 5.略 6.6 先由面积公式,求出AD=8. 7.或 先说明此三角形为直角三角形,但因为谁是斜边没有确定,故有两种情况.
8. 9.12cm 10.12cm 11.C 12.C 13.A ,则. 14.C ,得∠BAC=90°,由勾股定理可求得BC=10. 15.B ∵△ADB的AD边上的高为BC,∴.即,∴BC=4.在Rt△BCD中求得CD=3. 16.B 17.C 18.(1)③ (2)可能为0. (3)△ABC为直角三角形或等腰三角形 19.几个题的解法均有问题.(1)错误的原因是没有弄清哪个角是直角,盲目地运用勾股定理,当∠B=90°,应该有. (2)没有确定所求得的边是直角边,还是斜边.(3)考虑不完整,忽视了高AD在△ABC外部的情况. 20.3或 21.(1) (2) (3)按完全平方公式展形,进行证明即可. 22.∵,∴,∴△ABC为直角三角形,∴. 23.(1)4.8.先求出BC=8.则由面积公式可求出CD. (2)3.84 在△ACD中求得AD=3.6,所以BD=6.4,在△BCD中运用面积公式求DE,即.则. 24.(1)4 由面积公式,得. (2)等腰三角形.在Rt△ABD中,AB=5,AD=4,则BD=3,因为E为BC的中点,∴BE=6,DE=3,AE=5=AB.△ABE为等腰三角形.
25.左边右边
26..
. ∵, ∴.
期中测试题
(时间90分钟,满分120分)
一、选择题(3分×10=30分)
1.已知xy=1,则的值为( )
A. B. C. D.
2.有理数a,b在数轴上的对应点如图所示,则代数式的值为( )
A.正数 B.负数 C.零 D.不能确定
3.若分式的值为零,则x的值为( )
A.3 B.3或—3 C.—3 D.0
4.化简的结果是( )
A. B. C. D.
5.若x<2,则的值为( )
A.—1 B.0 C.1 D.2
6.中,x,y都扩大10倍,则分式的值( )
A.扩大10倍 B.缩小10倍 C.保持不变 D.缩小5倍
7.如果反比例函数的的图象经过点(3,2),那么下列各点中在此函数图象上的点是( )
A. B.
C. D.
8.一个矩形的面积是6,则这个矩形的一组邻边长x与y的函数关系图象大致是( )
9.若直角三角形的三边长分别为2,4,x,则x可能的值有( )
A.1个 B.2个 C.3个 D.4个
10.一等腰直角三角形的周长为2P,其面积为( )
A. B.
C. D.
二、填空题(3分×10=30分)
11.在分式中,x=______________时,分式无意义,当x=____________时,分式的值为零.
12.当时,.
13.若去分母解方程,出现增根,则增根为_____________.
14.在分式中,当x=_____________时,分式的值为1;当x的值____________时,分式值为正数.
15.已知,且,则.
16.反比例函数的图象经过点P,如图所示.根据图象可知,反比例函数的解析式为____________.
17.某蓄电池的电压为定值,如图所示的是该蓄电池电流I(A)与电阻R(Ω)之间的函数关系图象,则其函数解析式是______________.
18.近视眼镜的度数y(度)与镜片焦距x(m)成反比例关系,已知400度近视眼镜片的焦距为0.25m,则眼镜度数y与镜片焦距x之间的函数关系式为___________.
19.如图,已知△ABC中,∠ACB=90°,以△ABC的各边为边在△ABC外作三个正方形,分别表示这三个正方形的面积,,则.
20.如图,为了求出湖两岸A,B两点之间的距离,观测者从观测点A,B分别测得∠BAC=90°,∠ABC=30°,又测得BC=160m,则A,B两点之间的距离为__________m(结果保留根号).
三、解答题(60分)
21.先化简,再求值.(5分×2=10分)
(1),其中.
(2),其中.
22.解分式方程.(5分×2=10分)
(1) (2).
23.(8分)在Rt△ABC中,∠C=90°,,AB=2,求这个三角形的面积.
24.(8分)如图,铁路上A,B两点相距25km,C,D为两村庄,DA⊥AB于A,CB⊥AB于B,已知DA=15km,CB=10km,现在要在铁路AB上建一个土特产品收购站E,使得C,D两村到E站的距离相等,则E站应建在距A站多少千米处?
25.(8分)如图,已知Rt△ABC的顶点A是一次函数y=x+m与反比例函数的图象在第一象限内的交点,且.该一次函数与反比例函数的解析式是否能完全确定?如能确定,请写出它们的解析式;如不能确定,请说明理由.
26.列方程解应用题.(8分×2=16分)
(1)某厂原计划在规定期限内生产通信设备60台支援抗洪,由于改进了操作技术,每天生产的台数比原计划多50%,结果提前两天完成任务,求改进操作技术后每天生产通信设备多少台.
(2)为了方便广大游客到昆明参加“世博会”,铁道部门临时增开了一列南宁—昆明的直达快车,已知南宁—昆明两地相距828km,一列普通列车与一列直达快车都由南宁开往昆明,直达快车的平均速度是普通列车平均速度的1.5倍.直达快车比普通列车晚出发2h,比普通列车是4h到达昆明.求两车的平均速度.
参 考 答 案
1.D 2.A 3.C 4.B 5.A 6.C 7.B 8.D 9.B
10.C 11.—1;1 12.1 13.x=3 14.2;大于 15. 16. 17. 18. 19.144 20. 21.(1)原式 (2)原式 22.(1)x=1为增根,原方程无解 (2)x=2. 23.将两边平方,得,即.∴.∴4+2AC·BC=6.∴AC·BC=1.∴. 24.设AE=x km,由勾股定理,得,解得x=10. 25.设B(a,0),则,其中a>0,m>0.在Rt△ABO中,.则.∴m=6.所以一次函数的解析式为y=x+6.反比例函数的解析式为.
26.(1)设原计划每天生产通信设备x台,那么改进操作技术后每天生产1.5x台,依题意,得,解得x=10.经检验,x=10是原方程的解.当x=10时,1.5x=15. (2)设普通列车的平均速度为x km/h,则直达快车的平均速度为1.5x km/h,依题意,得,解得x=46.经检验,x=46是原方程的解.∴x=46,1.5x=69.
在本章中,我们探索了直角三角形的三边关系,并在此基础上得到了勾股定理,并学习了如何利用拼图验证勾股定理,介绍了勾股定理的用途;本章后半部分学习了勾股定理的逆定是以及它的应用.其知识结构如下:
在学习勾股定理时应注重知识的形成过程,即勾股定理的探索过程,有意识地培养自己探索新知识的能力.在运用勾股定理时一定要有直角三角形这个前提条件,因此,通过有关具体问题时,有时需添加适当的辅助线以构造直角三角形来帮助解题.
勾股定理的逆定理是用来判定一个三角形是否是直角三角形的,但在判定一个三角形是否是直角三角形时应首先确定该三角形的最大边,当其余两边的平方和等于最大边的平方时,该三角形才是直角三角形.勾股定理的逆定理也可用来证明两直线是否垂直,这一点同学们也应牢牢掌握.
典例精讲
例1 如图,有一块直角三角形纸片,两直角边AC=6cm,BC=8cm,现将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AE重合,求CD长.
方法指导:可设CD长为xcm,再寻找等量关系利用方程思想来解,而在直角三角形中,等量关系往往是勾股定理表达式.
解:设CD=xcm,则BD=BC—CD=(8—x)cm.
由题知△ACD与△AED关于AD对称,
∴AE=AC=6cm,DE=CD=xcm,∠AED=∠C=90°.
在Rr△ACB中,由勾股定理得:,
∴BE=AB—AE=10—6=4cm.
在Rt△BED中,由勾股定理得:.
∴,解得x=3cm.
方法总结:折叠问题应把握折叠前后两部分图形关于折痕对称,从而可以利用对称的有关性质来帮助解题目.
例2 已知:如图△ABC中,AB=AC=10,BC=16,点D在BC上,DA⊥CA于A.
求:BD的长.
方法指导:可设BD长为xcm,然后寻找含x的等式即可,由AB=AC=10知△ABC为等腰三角形,可作高利用其“三线合一”的性质来帮助建立方程.
解:设BD长为xcm.过点A作AE⊥BC于E,
∵AB=AC=10,∴△ABC为等腰三角形,
∴,
在△AEC中,由勾股定理得:.
在Rt△AED中,,
在Rt△DAC中,,
∴.解得.
方法总结:勾股定理通常与等腰三角形的性质结合起来使用.
举一反三 如图:A、B两点与建筑物底部D在一直线上,从建筑物顶部C点测得A、B两点的俯角分别是30°、60°,且AB=20cm,求建筑物CD的高.
解:
例3 甲、乙两船同时从港口A出发,甲船以12海里/时的速度向北偏东35°航行,乙船向南偏东55°航行.2小时后,甲船到达C岛,乙船到达B岛,若C、B两船相距40海里,问乙船的速度是每小进多少海里?
方法指导:可根据题意画出图形,易知△ABC是直角三角形,利用勾股定理求出AB距离,从而求出乙船速度.
解:由题知△ABC是直角三角形且∠BAC为直角.
∴,BC=40.
由勾股定理得(海里).
∴乙船速度为:(海里/时).
方法总结:凡是实际问题,应根据题意构造直角三角形来求解.
举一反三 “中华人民共和国道路交通管理条例”规定,小汽车在城街路上行驶速度不得超过70km/h,如图,一辆小汽车在一条城市街路上直道行驶,某一时刻刚好行驶到路面对车速检测仪正前方30m处,过了2s后,测得小汽车与速速检测仪间距离为50m,这辆小汽车超速了吗?
解:因为小汽车的速度为:,因此小汽车超速了.
例4 如图,海中有一小岛A,在该岛周围10海里内有暗礁,今有货船由西向东航行,开始在A岛南偏西45°的B处往东航行20海里后达到该岛南偏西30°的C处,之后继续向东航行,你认为货船继续向东航行会有触礁的危险吗?计算后说明理由.
方法指导:要想知道有无触礁危险只需算出点A到BC的距离,再比较即知.
解:过点A作AD⊥BC,垂足为D.
由题知:∠BAD=45°,∠CAD=30°.
设AD=x(海里),则BD=x(海里),CD=(x—20)(海里),
我们知道有一内角为30°的直角三角形三边比值为.
∴,即.
解得.
故无触礁危险.
方法总结:此题若直接用勾股定理也可得关于x的方程,但是是一元二次的,目前无法解出来,故应熟记特殊直角三角形的三边比值,如等腰直角三角形三边比值为.
举一反三 如图,点A是一个半径为300m的圆形森林公园的中心,在森林公园附近有B、C两个村庄,现要在B、C两村庄之间修一条长为1000m的笔直公路将两村连通.经测得∠ABC=45°,∠ACB=30°,问此公路是否会穿过该森林公园?请通过计算进行说明.
解:不会穿过公园.
例5 一架方梯长25m,如图,斜靠在一面墙上,梯子底端离墙7m,求:(1)这个梯子的顶端距地面有多高?(2)如果梯子的顶端下滑了4m,那么梯子的底端在水平方向滑动了几米?
方法指导:梯子靠在墙上即构成直角三角形,可利用勾股定理来求解.
解:(1)如图,在Rt△POQ中,由勾股定理得:
.
即梯子的顶端距离地面24m;
(2)由题知梯子底端移动的距离为OB,
设QB=x,则OA=OP—AP=24—4=20m,
梯子下滑过程中长度不变即AB=QP=25m,
在Rr△AOB中,由勾股定理得:
.
∴QB=OB—OQ=15—7=8m.
即梯子底端移动了8m.
方法总结:这是一类“梯子下滑问题”,解此类题应把握两点:梯子靠在墙上即构成直角三角形;梯子滑动过程中长度不变.
举一反三 如图,一个梯子AB长2.5m,顶端A靠在墙AC上,这时梯子下端B与墙角C距离为1.5m,梯子滑动后停在DE的位置上,测得BD长为0.5m,求梯子顶端A下落了多少m?
解:梯子顶端A下落了0.5m.
例6 若△ABC的三边分别为a、b、c,且满足,那么△ABC是何种形状?
解:由得
,
即,
∴a=3,b=4,c=5.
∵,由勾股定理逆定理知△ABC是直角三角形.
方法总结:要判断三角形形状,应寻找三边关系或三角之间的关系再作出判断.
举一反三 若a、b、c为△ABC的三边,且满足.探索△ABC的形状,并说明理由.
解:等边三角形.
例7 如图,CD是△ABC的AB边上的高,且有.求证:△ABC是直角三角形.
方法指导:先依题意画图,再利用勾股定理的逆定理来证.
解:在Rt△ACD中,由勾股定理得:
.
∴,同理,,
.
由勾股定理逆定理知:△ABC是直角三角形.
方法总结:证明直角三角形或两直线的垂直关系通常用勾股定理逆定理来解决.
举一反三 如图,已知在△ABC中,∠C=90°,D为AC上一点,与 有怎样的关系?试证明你的结论.
解:相等(提示:可证明,再作移项变形.)
本章综合练习
(时间90分钟,满分120分)
一、填空题(3分×10=30分)
1.在△ABC中,∠C=90°,a,b,c为∠A,∠B,∠C的对边.
(1)c=25,b=24,那么a=_________.
(2)a=30,b=16,那么c=_________.
2.在△ABC中,a,b,c为∠A,∠B,∠C的对边.
(1),那么当c=___________时,∠B=90°.
(2),那么当b=____________时,∠C=90°.
3.在△ABC中,∠C=90°,AB=40,AC=24.则斜边AB上的高是__________.
4.在△ABC中,a,b,c为∠A,∠B,∠C的对边,如果a,b,c满足,那么△ABC是以____________为斜边的直角三角形.
5.如图,每个小正方形的边长是1,在图中画出:
(1)一个面积为2的直角三角形.
(2)一个面积为2的正方形.
6.如图,△ABC中,BC=12,AB=10,△ABC的面积是48.那么BD=__________.
7.一个三角形的一个外角等于和它相邻的内角,如果此三角形的两条边长分别是5,2,那么以第三条边为半径的圆的面积是___________(保留).
8.边长为2的正三角形的面积为__________,边长为a的正三角形面积为___________.
9.如果梯子的底端离建筑物9m,那么15m长的梯子可以到达建筑物的高度是_________.
10.为得到湖两岸A点和B点间的距离,一个观测者在C点设桩,使∠ABC为直角(如图),并测得AC长20m、BC长16m,A,B两点间的距离是_________.
二、选择题(7分×3=21分)
11.有下列命题:
(1)如果a,b,c为一组勾股数,那么4a,4b,4c仍是勾股数;
(2)如果直角三角形的两边长是3,4,那么斜边必是5;
(3)如果一个三角形的三边是12,25,21,那么此三角形必是直角三角形;
(4)一个等腰直角三角形的三边长为a,b,c(a>b>c),那么.其中正确的是( )
A.(1)(2) B.(1)(3) C.(1)(4) D.(2)(4)
12.如图,△ABC中,AB=AC,AD⊥BC,垂足是D,AB=13,BD=5,则△ABC的面积是( )
A.65 B.120 C.60 D.36
13.如图,△ABC中,∠ACB=90°,AC=BC,如果△ABC的面积是8,那么腰长是( )
A.4 B.2 C.8 D.16
14.如图,B在A的北偏西α方向的6m处,C在A的北偏东β方向的8m处,并且,那么B、C两点相距( )
A.6m B.8m C.10m D.12m
15.如图,在Rt△ABC中,∠C=90°,D为AC上的一点,且有DA=DB=5,又△DAB的面积是10,那么DC的长是( )
A.4 B.3 C.5 D.4.5
16.在△ABC中,AB=AC,如果AB=17,BC=16,则BC边上的中线长是( )
A.8 B.15 C.10 D.6
17.如图,在Rt△ABC中,∠B=90°.以AC为直径的圆恰好过点B.AB=8,BC=6,则阴影部分的面积是( )
A. B.
C. D.
三、阅读理解题(5分)
18.阅读下列解题过程,并回答问题.
已知a,b,c为△ABC的三边,且满足,试判定△ABC的形状.
解:∵, ①
∴. ②
∴, ③
∴△ABC是直角三角形.
(1)上述解题过程,从哪一步开始出现错误?请写出代号___________.
(2)错误的原因为__________.
(3)本题正确结论为____________.
四、解答题(64分)
19.(8分)下面同学对各题的解答是否正确?为什么?
(1)在Rt△ABC中,∠B=90°,a=3,b=4,求c;
(2)已知直角三角形两条直角边为40和9,求第三边的长;
(3)已知△ABC中,AB=10,AC=17,BC边上的高AD=8,求BC的长.
解:(1)由勾股定理得:
,
∴.
(2)由勾股定理得:
,
∴,
∴c=41,
答:第三边的长为41.
(3)根据勾股定理:
,∴DB=8;
,∴DC=15.
故BC=15+8=24.
20.(8分)有一个三角形两边长分别为4和5,要使三角形为直角三角形,则第三边为多少?
21.(8分)给出一组式子:.
(1)你能发现关于上式中的一些规律吗?
(2)请你运用所发现的规律,给出第5个式子.
(3)请你证明你所发现的规律.
22.(8分)在△ABC中,已知a=15,b=17,c=8,求△ABC的面积.
23.(8分)如图,在△ABC中,∠ACB=90°,CD⊥AB,D为垂足,DE⊥BC,E为垂足,已知AC=6,AB=10.
求(1)CD的长;(2)DE的长.
24.(8分)如图,△ABC中,AD⊥BC,D为垂足,AE为BC边上的中线,已知AB=5,BC=12,△ABC的面积是24.
求(1)AD的长;
(2)判断△ABE的形状,并说明理由.
25.(8分)如图,在△ABC中,∠ACB=90°,CD为AB边上的高.试说明.
26.(8分)如图,在△ABC中,AM是BC边的中线,AE为BC边上的高.试判断与的关系,并说明理由.
参 考 答 案
1.(1)7 (2)34 2.(1)1 (2)3 3.19.2 4.a 5.略 6.6 先由面积公式,求出AD=8. 7.或 先说明此三角形为直角三角形,但因为谁是斜边没有确定,故有两种情况.
8. 9.12cm 10.12cm 11.C 12.C 13.A ,则. 14.C ,得∠BAC=90°,由勾股定理可求得BC=10. 15.B ∵△ADB的AD边上的高为BC,∴.即,∴BC=4.在Rt△BCD中求得CD=3. 16.B 17.C 18.(1)③ (2)可能为0. (3)△ABC为直角三角形或等腰三角形 19.几个题的解法均有问题.(1)错误的原因是没有弄清哪个角是直角,盲目地运用勾股定理,当∠B=90°,应该有. (2)没有确定所求得的边是直角边,还是斜边.(3)考虑不完整,忽视了高AD在△ABC外部的情况. 20.3或 21.(1) (2) (3)按完全平方公式展形,进行证明即可. 22.∵,∴,∴△ABC为直角三角形,∴. 23.(1)4.8.先求出BC=8.则由面积公式可求出CD. (2)3.84 在△ACD中求得AD=3.6,所以BD=6.4,在△BCD中运用面积公式求DE,即.则. 24.(1)4 由面积公式,得. (2)等腰三角形.在Rt△ABD中,AB=5,AD=4,则BD=3,因为E为BC的中点,∴BE=6,DE=3,AE=5=AB.△ABE为等腰三角形.
25.左边右边
26..
. ∵, ∴.
期中测试题
(时间90分钟,满分120分)
一、选择题(3分×10=30分)
1.已知xy=1,则的值为( )
A. B. C. D.
2.有理数a,b在数轴上的对应点如图所示,则代数式的值为( )
A.正数 B.负数 C.零 D.不能确定
3.若分式的值为零,则x的值为( )
A.3 B.3或—3 C.—3 D.0
4.化简的结果是( )
A. B. C. D.
5.若x<2,则的值为( )
A.—1 B.0 C.1 D.2
6.中,x,y都扩大10倍,则分式的值( )
A.扩大10倍 B.缩小10倍 C.保持不变 D.缩小5倍
7.如果反比例函数的的图象经过点(3,2),那么下列各点中在此函数图象上的点是( )
A. B.
C. D.
8.一个矩形的面积是6,则这个矩形的一组邻边长x与y的函数关系图象大致是( )
9.若直角三角形的三边长分别为2,4,x,则x可能的值有( )
A.1个 B.2个 C.3个 D.4个
10.一等腰直角三角形的周长为2P,其面积为( )
A. B.
C. D.
二、填空题(3分×10=30分)
11.在分式中,x=______________时,分式无意义,当x=____________时,分式的值为零.
12.当时,.
13.若去分母解方程,出现增根,则增根为_____________.
14.在分式中,当x=_____________时,分式的值为1;当x的值____________时,分式值为正数.
15.已知,且,则.
16.反比例函数的图象经过点P,如图所示.根据图象可知,反比例函数的解析式为____________.
17.某蓄电池的电压为定值,如图所示的是该蓄电池电流I(A)与电阻R(Ω)之间的函数关系图象,则其函数解析式是______________.
18.近视眼镜的度数y(度)与镜片焦距x(m)成反比例关系,已知400度近视眼镜片的焦距为0.25m,则眼镜度数y与镜片焦距x之间的函数关系式为___________.
19.如图,已知△ABC中,∠ACB=90°,以△ABC的各边为边在△ABC外作三个正方形,分别表示这三个正方形的面积,,则.
20.如图,为了求出湖两岸A,B两点之间的距离,观测者从观测点A,B分别测得∠BAC=90°,∠ABC=30°,又测得BC=160m,则A,B两点之间的距离为__________m(结果保留根号).
三、解答题(60分)
21.先化简,再求值.(5分×2=10分)
(1),其中.
(2),其中.
22.解分式方程.(5分×2=10分)
(1) (2).
23.(8分)在Rt△ABC中,∠C=90°,,AB=2,求这个三角形的面积.
24.(8分)如图,铁路上A,B两点相距25km,C,D为两村庄,DA⊥AB于A,CB⊥AB于B,已知DA=15km,CB=10km,现在要在铁路AB上建一个土特产品收购站E,使得C,D两村到E站的距离相等,则E站应建在距A站多少千米处?
25.(8分)如图,已知Rt△ABC的顶点A是一次函数y=x+m与反比例函数的图象在第一象限内的交点,且.该一次函数与反比例函数的解析式是否能完全确定?如能确定,请写出它们的解析式;如不能确定,请说明理由.
26.列方程解应用题.(8分×2=16分)
(1)某厂原计划在规定期限内生产通信设备60台支援抗洪,由于改进了操作技术,每天生产的台数比原计划多50%,结果提前两天完成任务,求改进操作技术后每天生产通信设备多少台.
(2)为了方便广大游客到昆明参加“世博会”,铁道部门临时增开了一列南宁—昆明的直达快车,已知南宁—昆明两地相距828km,一列普通列车与一列直达快车都由南宁开往昆明,直达快车的平均速度是普通列车平均速度的1.5倍.直达快车比普通列车晚出发2h,比普通列车是4h到达昆明.求两车的平均速度.
参 考 答 案
1.D 2.A 3.C 4.B 5.A 6.C 7.B 8.D 9.B
10.C 11.—1;1 12.1 13.x=3 14.2;大于 15. 16. 17. 18. 19.144 20. 21.(1)原式 (2)原式 22.(1)x=1为增根,原方程无解 (2)x=2. 23.将两边平方,得,即.∴.∴4+2AC·BC=6.∴AC·BC=1.∴. 24.设AE=x km,由勾股定理,得,解得x=10. 25.设B(a,0),则,其中a>0,m>0.在Rt△ABO中,.则.∴m=6.所以一次函数的解析式为y=x+6.反比例函数的解析式为.
26.(1)设原计划每天生产通信设备x台,那么改进操作技术后每天生产1.5x台,依题意,得,解得x=10.经检验,x=10是原方程的解.当x=10时,1.5x=15. (2)设普通列车的平均速度为x km/h,则直达快车的平均速度为1.5x km/h,依题意,得,解得x=46.经检验,x=46是原方程的解.∴x=46,1.5x=69.
