4.4用尺规作三角形(教学课件)-七年级数学下册同步课件(北师大版)
文档属性
| 名称 | 4.4用尺规作三角形(教学课件)-七年级数学下册同步课件(北师大版) |

|
|
| 格式 | pptx | ||
| 文件大小 | 330.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-31 00:00:00 | ||
图片预览





文档简介
(共24张PPT)
北师大版 数学 七年级下册
4 用尺规作三角形
第四章 三角形
学习目标
1.在分别给出两边及其夹角、两角及其夹边和三边的条件下,能够利用尺规作出三角形.(重点,难点)
2.了解作图方法的合理性.
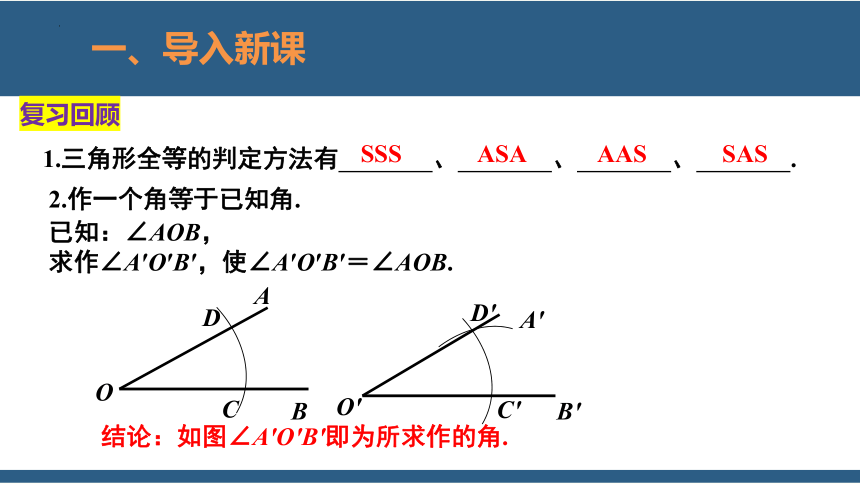
已知:∠AOB,
求作∠A′O′B′,使∠A′O′B′=∠AOB.
O
B
A
2.作一个角等于已知角.
1.三角形全等的判定方法有 、 、 、 .
SSS
ASA
AAS
SAS
一、导入新课
复习回顾
C
D
O′
B′
A′
D′
C′
结论:如图∠A′O′B′即为所求作的角.
一、导入新课
情境导入
小明书上的三角形被墨迹污染了一部分,他想在作业本上画出一个与书上完全一样的三角形,他该怎么办?
我们已经会用尺规作一条线段等 于已知线段、作一个角等于已知角.而边和角是三角形的基本元素,那么你能利用尺规作一个三角形与已知三角形全等吗?
二、新知探究
探究一:已知两边及其夹角作三角形
已知:线段a、c,∠α.
求作:△ABC,使BC=a,AB=c,∠ABC=∠α.
a
c
α
做一做:
1.已知三角形的两边及其夹角,求作这个三角形.
二、新知探究
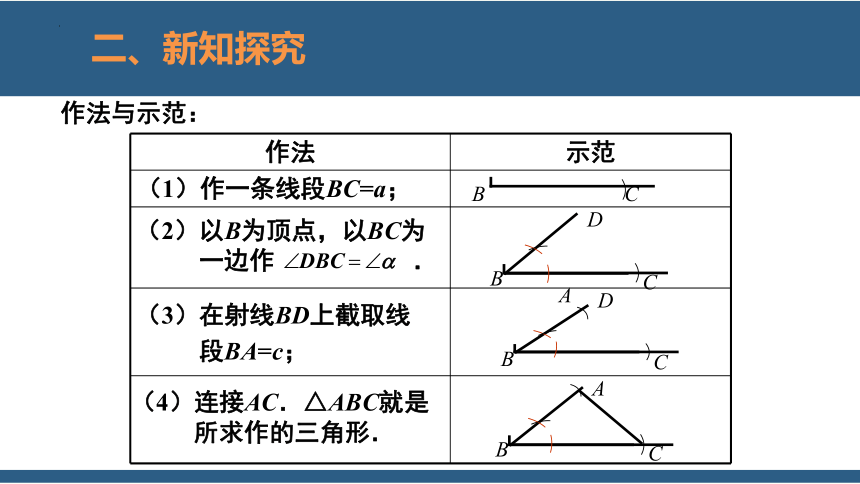
作法 示范
(1)作一条线段BC=a;
(2)以B为顶点,以BC为
一边作 .
B
C
B
C
B
C
B
C
(3)在射线BD上截取线
段BA=c;
(4)连接AC.△ABC就是
所求作的三角形.
A
D
D
A
作法与示范:
二、新知探究
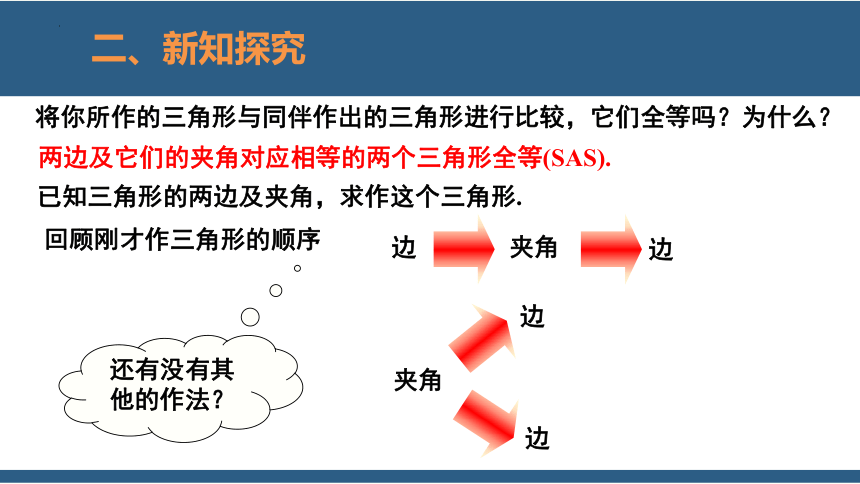
将你所作的三角形与同伴作出的三角形进行比较,它们全等吗?为什么?
两边及它们的夹角对应相等的两个三角形全等(SAS).
已知三角形的两边及夹角,求作这个三角形.
回顾刚才作三角形的顺序
边
边
夹角
夹角
边
边
还有没有其他的作法?
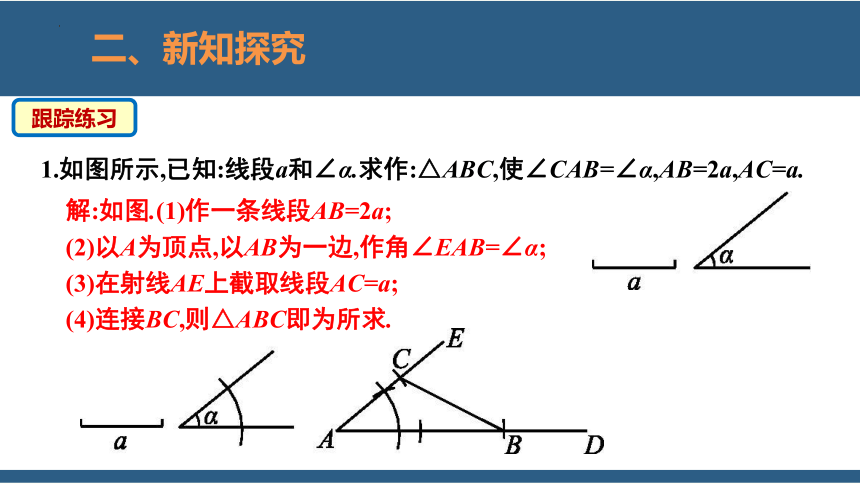
1.如图所示,已知:线段a和∠α.求作:△ABC,使∠CAB=∠α,AB=2a,AC=a.
二、新知探究
跟踪练习
解:如图.(1)作一条线段AB=2a;
(2)以A为顶点,以AB为一边,作角∠EAB=∠α;
(3)在射线AE上截取线段AC=a;
(4)连接BC,则△ABC即为所求.
二、新知探究
做一做:
2.已知三角形的两角及其夹边,求作这个三角形.
已知:∠α,∠β,线段c .
c
α
β
求作:△ABC,使得∠A=∠α,∠B=∠β,AB=c.
探究二:已知两角及其夹边作三角形
二、新知探究
请按照给出的作法作出相应的图形.
作法 图形
(1)作 ;
(2)在射线AF上截取线段AB=c;
(3)以B为顶点,以BA为一边,
作 ,BE交AD于点C.
△ABC就是所求作的三角形.
2.如图所示,已知线段a和∠α,用尺规作△ABC,使BC=a,∠B=∠α,∠C=2∠α.
二、新知探究
跟踪练习
解:如图,△ABC就是所求作的三角形.
B
M
二、新知探究
做一做:3.已知三角形的三边,求作这个三角形.
已知:线段a,b,c.
求作:△ABC,使得AB=c,AC=b,BC=a.
a
b
c
(3)分别以B,C为圆心,以c,b为半径画弧,两弧交于A点;
(4)连接AB,AC,
作法:(1)作一条射线BM,
则△ABC就是所求作的三角形.
A
探究三:已知三边作三角形
C
(2)在射线BM上截取线段BC=a;
(1)用尺规作三角形,实质是用没有刻度的直尺和圆规作一个角等于已知角,作一条线段等于已知线段的应用.
(2)用尺规作三角形的常见类型:
①已知两边及其夹角作三角形(SAS);
②已知两角及其夹边作三角形(ASA);
③已知三边作三角形(SSS).
二、新知探究
知识归纳
3.如图所示,已知线段a,b,用尺规作△ABC,使AC=a,AB=b,BC=2b-a.(不写作法,保留作图痕迹)
二、新知探究
跟踪练习
解:如图所示,△ABC即为所求.
二、新知探究
知识归纳
用尺规作三角形的技巧:
1.假设所求作的图形已经作出,并在草稿纸上作出草图;
2.在草图上标出已给的边、角的对应位置;
3.从草图中首先找出基本图形,由此确定作图的起始步骤;
4.在3的基础上逐步向所求图形扩展.
例1:给出下列关于三角形的条件:
①已知三角;
②已知两边;
③已知两角及其夹边;
④已知两边及其中一边的对角.利用尺规作图,
能作出唯一三角形的是 .(填序号)
③
三、典例精析
三、典例精析
例2:如图所示,已知线段a,b,求作:△ABC,使BC=a,AC=AB=b.
解:作法:如图,(1)作射线BE;
(2)在射线BE上截取BC=a;
(3)分别以点B,C为圆心,b为半径画弧,
两弧在射线BE的同侧交于点A.
(4)连接AB,AC,则△ABC就是所求作的三角形.
2.如图是作△ABC的作图痕迹,则此作图的已知条件是( )
A.已知两边及夹角
B.已知三边
C.已知两角及夹边
D.已知两边及一边的对角
四、当堂练习
1.用尺规作图,下列条件中可能作出两个不同三角形的是( )
A.已知两边及其夹角 B.已知两边及其中一边的对角
C.已知两角及其夹边 D.已知三条边
B
C
3.如图①,已知线段a,∠1,求作△ABC,使BC=a,∠ABC= ∠BCA=∠1,张蕾的作法如图②所示,则下列说法中一定正确的是 ( )
A.作△ABC的依据为ASA
B.弧EF是以AC长为半径画的
C.弧MN是以点A为圆心,a为半径画的
D.弧GH是以CP长为半径画的
四、当堂练习
A
四、当堂练习
4.已知线段a,b,c,求作△ABC,使BC=a,AC=b,AB=c,下列作法的合理顺序为 (填序号).
①分别以点B,C为圆心,c,b为半径在BC的同侧作弧,两弧交于点A;
②作射线BM,在BM上截取BC=a;
③连接AB,AC,则△ABC就是所求作的三角形.
②①③
5.已知:线段a,∠α(如图).
求作:△ABC,使AB=AC=a,∠B=∠α.
四、当堂练习
结论:如图所示,△ABC即为所求作的三角形.
四、当堂练习
解:如图所示,△A1B1C1即为所求.
6.如图所示,△ABC被污渍污染了,请你重新作一个△A1B1C1,使△A1B1C1≌△ABC(要求:用尺规作图,不写作法,但要保留作图痕迹).
五、课堂小结
用尺规作三角形的常见类型:
①已知两边及其夹角作三角形(SAS);
②已知两角及其夹边作三角形(ASA);
③已知三边作三角形(SSS).
用尺规作三角形的技巧:
1.假设所求作的图形已经作出,并在草稿纸上作出草图;
2.在草图上标出已给的边、角的对应位置;
3.从草图中首先找出基本图形,由此确定作图的起始步骤;
4.在3的基础上逐步向所求图形扩展.
六、作业布置
习题4.9
北师大版 数学 七年级下册
4 用尺规作三角形
第四章 三角形
学习目标
1.在分别给出两边及其夹角、两角及其夹边和三边的条件下,能够利用尺规作出三角形.(重点,难点)
2.了解作图方法的合理性.
已知:∠AOB,
求作∠A′O′B′,使∠A′O′B′=∠AOB.
O
B
A
2.作一个角等于已知角.
1.三角形全等的判定方法有 、 、 、 .
SSS
ASA
AAS
SAS
一、导入新课
复习回顾
C
D
O′
B′
A′
D′
C′
结论:如图∠A′O′B′即为所求作的角.
一、导入新课
情境导入
小明书上的三角形被墨迹污染了一部分,他想在作业本上画出一个与书上完全一样的三角形,他该怎么办?
我们已经会用尺规作一条线段等 于已知线段、作一个角等于已知角.而边和角是三角形的基本元素,那么你能利用尺规作一个三角形与已知三角形全等吗?
二、新知探究
探究一:已知两边及其夹角作三角形
已知:线段a、c,∠α.
求作:△ABC,使BC=a,AB=c,∠ABC=∠α.
a
c
α
做一做:
1.已知三角形的两边及其夹角,求作这个三角形.
二、新知探究
作法 示范
(1)作一条线段BC=a;
(2)以B为顶点,以BC为
一边作 .
B
C
B
C
B
C
B
C
(3)在射线BD上截取线
段BA=c;
(4)连接AC.△ABC就是
所求作的三角形.
A
D
D
A
作法与示范:
二、新知探究
将你所作的三角形与同伴作出的三角形进行比较,它们全等吗?为什么?
两边及它们的夹角对应相等的两个三角形全等(SAS).
已知三角形的两边及夹角,求作这个三角形.
回顾刚才作三角形的顺序
边
边
夹角
夹角
边
边
还有没有其他的作法?
1.如图所示,已知:线段a和∠α.求作:△ABC,使∠CAB=∠α,AB=2a,AC=a.
二、新知探究
跟踪练习
解:如图.(1)作一条线段AB=2a;
(2)以A为顶点,以AB为一边,作角∠EAB=∠α;
(3)在射线AE上截取线段AC=a;
(4)连接BC,则△ABC即为所求.
二、新知探究
做一做:
2.已知三角形的两角及其夹边,求作这个三角形.
已知:∠α,∠β,线段c .
c
α
β
求作:△ABC,使得∠A=∠α,∠B=∠β,AB=c.
探究二:已知两角及其夹边作三角形
二、新知探究
请按照给出的作法作出相应的图形.
作法 图形
(1)作 ;
(2)在射线AF上截取线段AB=c;
(3)以B为顶点,以BA为一边,
作 ,BE交AD于点C.
△ABC就是所求作的三角形.
2.如图所示,已知线段a和∠α,用尺规作△ABC,使BC=a,∠B=∠α,∠C=2∠α.
二、新知探究
跟踪练习
解:如图,△ABC就是所求作的三角形.
B
M
二、新知探究
做一做:3.已知三角形的三边,求作这个三角形.
已知:线段a,b,c.
求作:△ABC,使得AB=c,AC=b,BC=a.
a
b
c
(3)分别以B,C为圆心,以c,b为半径画弧,两弧交于A点;
(4)连接AB,AC,
作法:(1)作一条射线BM,
则△ABC就是所求作的三角形.
A
探究三:已知三边作三角形
C
(2)在射线BM上截取线段BC=a;
(1)用尺规作三角形,实质是用没有刻度的直尺和圆规作一个角等于已知角,作一条线段等于已知线段的应用.
(2)用尺规作三角形的常见类型:
①已知两边及其夹角作三角形(SAS);
②已知两角及其夹边作三角形(ASA);
③已知三边作三角形(SSS).
二、新知探究
知识归纳
3.如图所示,已知线段a,b,用尺规作△ABC,使AC=a,AB=b,BC=2b-a.(不写作法,保留作图痕迹)
二、新知探究
跟踪练习
解:如图所示,△ABC即为所求.
二、新知探究
知识归纳
用尺规作三角形的技巧:
1.假设所求作的图形已经作出,并在草稿纸上作出草图;
2.在草图上标出已给的边、角的对应位置;
3.从草图中首先找出基本图形,由此确定作图的起始步骤;
4.在3的基础上逐步向所求图形扩展.
例1:给出下列关于三角形的条件:
①已知三角;
②已知两边;
③已知两角及其夹边;
④已知两边及其中一边的对角.利用尺规作图,
能作出唯一三角形的是 .(填序号)
③
三、典例精析
三、典例精析
例2:如图所示,已知线段a,b,求作:△ABC,使BC=a,AC=AB=b.
解:作法:如图,(1)作射线BE;
(2)在射线BE上截取BC=a;
(3)分别以点B,C为圆心,b为半径画弧,
两弧在射线BE的同侧交于点A.
(4)连接AB,AC,则△ABC就是所求作的三角形.
2.如图是作△ABC的作图痕迹,则此作图的已知条件是( )
A.已知两边及夹角
B.已知三边
C.已知两角及夹边
D.已知两边及一边的对角
四、当堂练习
1.用尺规作图,下列条件中可能作出两个不同三角形的是( )
A.已知两边及其夹角 B.已知两边及其中一边的对角
C.已知两角及其夹边 D.已知三条边
B
C
3.如图①,已知线段a,∠1,求作△ABC,使BC=a,∠ABC= ∠BCA=∠1,张蕾的作法如图②所示,则下列说法中一定正确的是 ( )
A.作△ABC的依据为ASA
B.弧EF是以AC长为半径画的
C.弧MN是以点A为圆心,a为半径画的
D.弧GH是以CP长为半径画的
四、当堂练习
A
四、当堂练习
4.已知线段a,b,c,求作△ABC,使BC=a,AC=b,AB=c,下列作法的合理顺序为 (填序号).
①分别以点B,C为圆心,c,b为半径在BC的同侧作弧,两弧交于点A;
②作射线BM,在BM上截取BC=a;
③连接AB,AC,则△ABC就是所求作的三角形.
②①③
5.已知:线段a,∠α(如图).
求作:△ABC,使AB=AC=a,∠B=∠α.
四、当堂练习
结论:如图所示,△ABC即为所求作的三角形.
四、当堂练习
解:如图所示,△A1B1C1即为所求.
6.如图所示,△ABC被污渍污染了,请你重新作一个△A1B1C1,使△A1B1C1≌△ABC(要求:用尺规作图,不写作法,但要保留作图痕迹).
五、课堂小结
用尺规作三角形的常见类型:
①已知两边及其夹角作三角形(SAS);
②已知两角及其夹边作三角形(ASA);
③已知三边作三角形(SSS).
用尺规作三角形的技巧:
1.假设所求作的图形已经作出,并在草稿纸上作出草图;
2.在草图上标出已给的边、角的对应位置;
3.从草图中首先找出基本图形,由此确定作图的起始步骤;
4.在3的基础上逐步向所求图形扩展.
六、作业布置
习题4.9
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
