5.3分式的加减法第3课时(同步课件)-八年级数学下册同步精品课堂(北师大版)
文档属性
| 名称 | 5.3分式的加减法第3课时(同步课件)-八年级数学下册同步精品课堂(北师大版) |

|
|
| 格式 | pptx | ||
| 文件大小 | 960.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-31 14:05:59 | ||
图片预览








文档简介
北师大版 数学 八年级下册
第3课时
第五章 分式与分式方程
3 分式的加减法
学习目标
1.复习并巩固分式的运算法则.(重点)
2.能熟练地进行分式的混合运算.(难点)
一、复习回顾
上述法则用式子表示为: .
1.同分母分式的加减法则
同分母分式相加减, 不变,把 相加减.
分母
分子
????????±????????=????±????????
?
2.异分母分式的加减法则
异分母的分式相加减,先 ,化为 的分式,然后再按同分母分式的加减法法则进行计算.
上述法则用式子表示为: .
通分
同分母
二、自主合作,探究新知
探究一:较复杂异分母分式的加减
先找出最简公分母,再正确通分,转化为同分母的分式相加减.
注意:分母是多项式先分解因式.
解:原式
做一做:计算:(1)????????????+????+?????????????????;
?
二、自主合作,探究新知
方法一:
原式
方法二:
原式
注意:对于整式与分式的加减运算,可以将整式的每一项的分母看成1,再通分,也可以把整式的分母整体看成1,再进行通分运算.
(2)????????????+?????????+????;
?
二、自主合作,探究新知
先找出最简公分母,再正确通分,转化为同分母的分式相加减.
解:原式
二、自主合作,探究新知
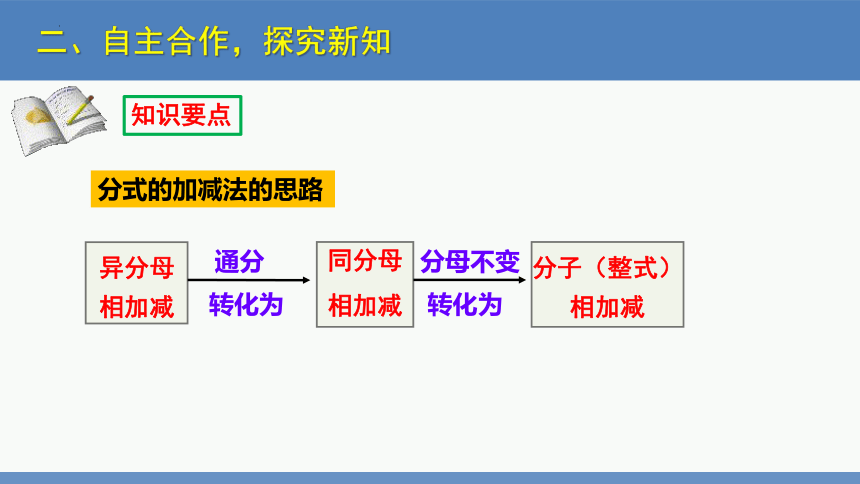
知识要点
分式的加减法的思路
通分
转化为
异分母相加减
同分母
相加减
分子(整式)相加减
分母不变
转化为
二、自主合作,探究新知
典型例题
还有其他解法吗?
例1:已知????????=????,求??????????????????????+??????????????????????????????的值.
?
解:原式=????(????+????)?????(?????????)??????????????????????????
=?????????????????????????
?
因为????????=????,即????=????????,
所以,原式=(????????)????(????????)?????????????=????????????????????????=????????.
?
总结:利用“整体代入”思想化简求值时,先把要求值的代数式化简,然后将已知条件变换成适合所求代数式的形式,再整体代入即可.
二、自主合作,探究新知
探究二:分式的混合运算
议一议:如何计算 ?
请先思考这道题包含的运算,确定运算顺序,再独立完成.
解:
先乘方,再乘除,最后加减.
知识要点
二、自主合作,探究新知
分式的混合运算顺序
先算乘方,再算乘除,最后算加减,有括号的先算括号里面的.
注意:计算结果要化为最简分式或整式.
(2)原式=(?????????????????)?????????+?????????????????
=??????????????????(????+????)(????+????)(?????????)
=???????????????????(????+????)(????+????)(?????????)
=-1
?
二、自主合作,探究新知
典型例题
例2 计算:(1)????????+??????????????????????÷????+?????????????????????+????; (2)(?????????????)÷?????????????????????+????.
?
解:(1)原式=????????+????????????????????????????????????????+????????+????
=????????+?????????(????+????)(?????????)?(?????????)????????+????
=????????+?????????(?????????)(????+????)????
=????+????(????+????)?????????(?????????)(????+????)????
=????+?????????(?????????)(????+????)????=?????+????(????+????)????
?
先算括号里的减法,再算括号外的除法.
二、自主合作,探究新知
分式的混合运算
(1)进行混合运算时,要注意运算顺序,在没有括号的情况下,按从左往右的方向,先算乘方,再算乘除,后算加减;
(2)分式的混合运算,一般按常规运算顺序,但有时应先根据题目的特点,运用乘法的运算律进行灵活运算.
混合运算的特点:是整式运算、因式分解、分式运算的综合运用,综合性强.
知识要点
二、自主合作,探究新知
探究三:分式加减法的实际应用
做一做:根据规划设计,某工程队准备修建一条长 1120 m 的盲道由于采用新的施工方式实际每天修建盲道的长度比原计划增加10 m,从而缩短了工期假设原计划每天修建盲道x m,那么
(1)原计划修建这条盲道需多少天?实际修建这条盲道用了多少天?
(2)实际修建这条盲道的工期比原计划缩短了几天?
解:(1)原计划修建这条盲道需要????????????????????天;实际修建这条盲道用了????????????????????+????????天.
?
(2)?????????????????????????????????????????+????????=????????????????(????+????????)?????????????????????????(????+????????)=????????????????????????(????+????????)
∴实际修建这条盲道的工期比原计划缩短了????????????????????????(????+????????)天.
?
运用分式解决实际问题时,用分式表示实际问题中的量是解决问题的关键.
三、即学即练,应用知识
D
D
C
三、即学即练,应用知识
C
三、即学即练,应用知识
三、即学即练,应用知识
三、即学即练,应用知识
四、课堂小结
2.分式的混合运算法则
1.分式加减运算的方法思路
通分
转化为
异分母相加减
同分母
相加减
分子(整式)相加减
分母不变
转化为
先算乘方,再算乘除,最后算加减,有括号的先算括号里面的.
注意:计算结果要化为最简分式或整式.
五、当堂达标检测
A
B
D
-2
五、当堂达标检测
5.计算:(1)??????????????????????????????+????????+????; (2)(????+????????+????)+??????????????????????.
?
解:(1)??????????????????????????????+????????+????
=????(????+????)(?????????)?????(????+????)????
=????(????+????)(????+????)????(?????????)?????(?????????)(????+????)????(?????????)
=????(????+????)?????(?????????)(????+????)????(?????????)
=????????+????(????+????)????(?????????)
?
五、当堂达标检测
五、当堂达标检测
教材习题5.6.
六、布置作业
第3课时
第五章 分式与分式方程
3 分式的加减法
学习目标
1.复习并巩固分式的运算法则.(重点)
2.能熟练地进行分式的混合运算.(难点)
一、复习回顾
上述法则用式子表示为: .
1.同分母分式的加减法则
同分母分式相加减, 不变,把 相加减.
分母
分子
????????±????????=????±????????
?
2.异分母分式的加减法则
异分母的分式相加减,先 ,化为 的分式,然后再按同分母分式的加减法法则进行计算.
上述法则用式子表示为: .
通分
同分母
二、自主合作,探究新知
探究一:较复杂异分母分式的加减
先找出最简公分母,再正确通分,转化为同分母的分式相加减.
注意:分母是多项式先分解因式.
解:原式
做一做:计算:(1)????????????+????+?????????????????;
?
二、自主合作,探究新知
方法一:
原式
方法二:
原式
注意:对于整式与分式的加减运算,可以将整式的每一项的分母看成1,再通分,也可以把整式的分母整体看成1,再进行通分运算.
(2)????????????+?????????+????;
?
二、自主合作,探究新知
先找出最简公分母,再正确通分,转化为同分母的分式相加减.
解:原式
二、自主合作,探究新知
知识要点
分式的加减法的思路
通分
转化为
异分母相加减
同分母
相加减
分子(整式)相加减
分母不变
转化为
二、自主合作,探究新知
典型例题
还有其他解法吗?
例1:已知????????=????,求??????????????????????+??????????????????????????????的值.
?
解:原式=????(????+????)?????(?????????)??????????????????????????
=?????????????????????????
?
因为????????=????,即????=????????,
所以,原式=(????????)????(????????)?????????????=????????????????????????=????????.
?
总结:利用“整体代入”思想化简求值时,先把要求值的代数式化简,然后将已知条件变换成适合所求代数式的形式,再整体代入即可.
二、自主合作,探究新知
探究二:分式的混合运算
议一议:如何计算 ?
请先思考这道题包含的运算,确定运算顺序,再独立完成.
解:
先乘方,再乘除,最后加减.
知识要点
二、自主合作,探究新知
分式的混合运算顺序
先算乘方,再算乘除,最后算加减,有括号的先算括号里面的.
注意:计算结果要化为最简分式或整式.
(2)原式=(?????????????????)?????????+?????????????????
=??????????????????(????+????)(????+????)(?????????)
=???????????????????(????+????)(????+????)(?????????)
=-1
?
二、自主合作,探究新知
典型例题
例2 计算:(1)????????+??????????????????????÷????+?????????????????????+????; (2)(?????????????)÷?????????????????????+????.
?
解:(1)原式=????????+????????????????????????????????????????+????????+????
=????????+?????????(????+????)(?????????)?(?????????)????????+????
=????????+?????????(?????????)(????+????)????
=????+????(????+????)?????????(?????????)(????+????)????
=????+?????????(?????????)(????+????)????=?????+????(????+????)????
?
先算括号里的减法,再算括号外的除法.
二、自主合作,探究新知
分式的混合运算
(1)进行混合运算时,要注意运算顺序,在没有括号的情况下,按从左往右的方向,先算乘方,再算乘除,后算加减;
(2)分式的混合运算,一般按常规运算顺序,但有时应先根据题目的特点,运用乘法的运算律进行灵活运算.
混合运算的特点:是整式运算、因式分解、分式运算的综合运用,综合性强.
知识要点
二、自主合作,探究新知
探究三:分式加减法的实际应用
做一做:根据规划设计,某工程队准备修建一条长 1120 m 的盲道由于采用新的施工方式实际每天修建盲道的长度比原计划增加10 m,从而缩短了工期假设原计划每天修建盲道x m,那么
(1)原计划修建这条盲道需多少天?实际修建这条盲道用了多少天?
(2)实际修建这条盲道的工期比原计划缩短了几天?
解:(1)原计划修建这条盲道需要????????????????????天;实际修建这条盲道用了????????????????????+????????天.
?
(2)?????????????????????????????????????????+????????=????????????????(????+????????)?????????????????????????(????+????????)=????????????????????????(????+????????)
∴实际修建这条盲道的工期比原计划缩短了????????????????????????(????+????????)天.
?
运用分式解决实际问题时,用分式表示实际问题中的量是解决问题的关键.
三、即学即练,应用知识
D
D
C
三、即学即练,应用知识
C
三、即学即练,应用知识
三、即学即练,应用知识
三、即学即练,应用知识
四、课堂小结
2.分式的混合运算法则
1.分式加减运算的方法思路
通分
转化为
异分母相加减
同分母
相加减
分子(整式)相加减
分母不变
转化为
先算乘方,再算乘除,最后算加减,有括号的先算括号里面的.
注意:计算结果要化为最简分式或整式.
五、当堂达标检测
A
B
D
-2
五、当堂达标检测
5.计算:(1)??????????????????????????????+????????+????; (2)(????+????????+????)+??????????????????????.
?
解:(1)??????????????????????????????+????????+????
=????(????+????)(?????????)?????(????+????)????
=????(????+????)(????+????)????(?????????)?????(?????????)(????+????)????(?????????)
=????(????+????)?????(?????????)(????+????)????(?????????)
=????????+????(????+????)????(?????????)
?
五、当堂达标检测
五、当堂达标检测
教材习题5.6.
六、布置作业
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
