22.9平面向量的减法(第1课时)(教学课件)-八年级数学下册同步精品课堂(沪教版)
文档属性
| 名称 | 22.9平面向量的减法(第1课时)(教学课件)-八年级数学下册同步精品课堂(沪教版) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-31 00:00:00 | ||
图片预览






文档简介
2023-2024学年八年级下册数学同步精品课堂(沪教版)
第 22章 四边形
22.9平面向量的减法(第1课时)
学习目标
1.通过实例理解向量加法的三角形法则及其几何意义;理解零向量的意义.
2.探究得出向量的加法满足交换律与结合律,并会用它们进行向量的运算.
3.知道向量加法的交换律与平行四边形的判定和性质定理之间的联系.
4.渗透类比的数学思想
一般来说,求不平行的两个向量的和向量时,只要把第二个向量与第一个向量首尾相接,那么以第一个向量的起点为起点、第二个向量的终点为终点的向量就是和向量.这样的规定叫做向量加法的三角形法则.
复习引入
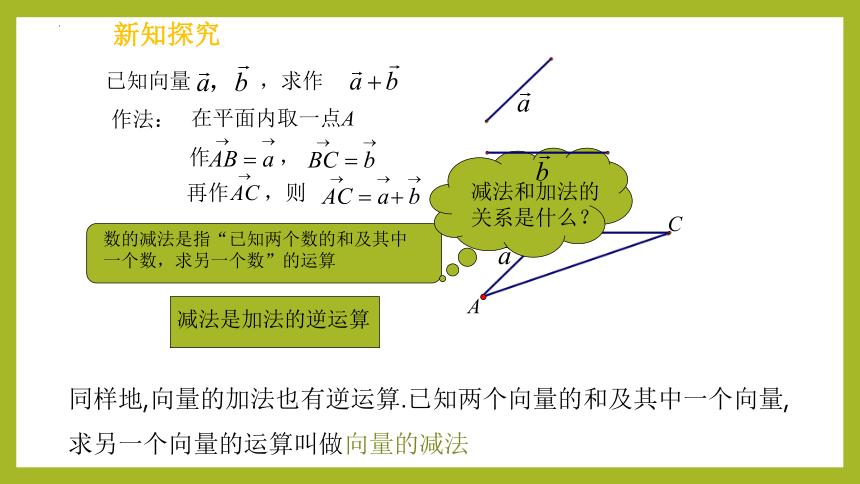
新知探究
再作 ,则
作 ,
已知向量 ,求作
作法:
在平面内取一点A
A
B
C
数的减法是指“已知两个数的和及其中一个数,求另一个数”的运算
减法和加法的关系是什么?
减法是加法的逆运算
同样地,向量的加法也有逆运算.已知两个向量的和及其中一个向量,求另一个向量的运算叫做向量的减法
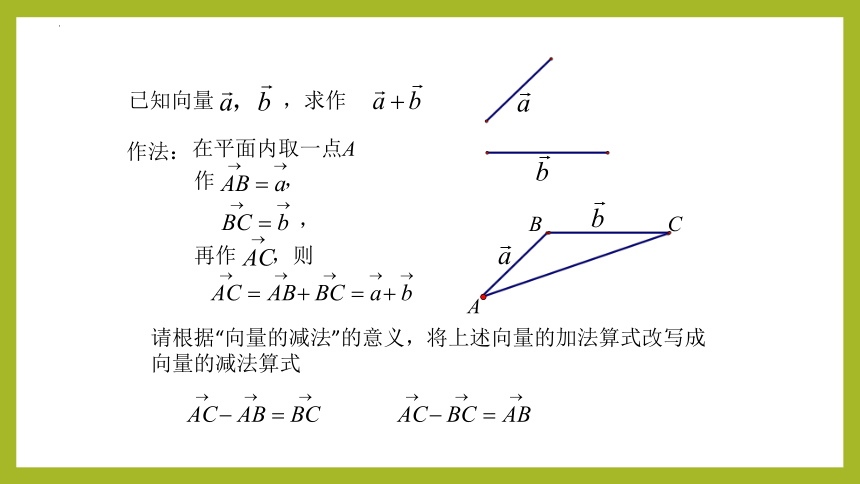
再作 ,则
作 ,
已知向量 ,求作
作法:
在平面内取一点A
,
A
B
C
请根据“向量的减法”的意义,将上述向量的加法算式改写成向量的减法算式。
观察,差向量 的起点和终点位置与被减向量 和减向量 的起点、终点的关系?
A
B
C
差向量的起点是__________的____点.
差向量的终点是__________的____点.
减向量
被减向量
终
终
已知两个向量,如何求作它们的差向量?
在平面内任取一点,以这点为公共起点作出这两个向量,那么它们的差向量是以减向量的终点为起点,被减向量的终点为终点的向量.
向量减法的三角形法则
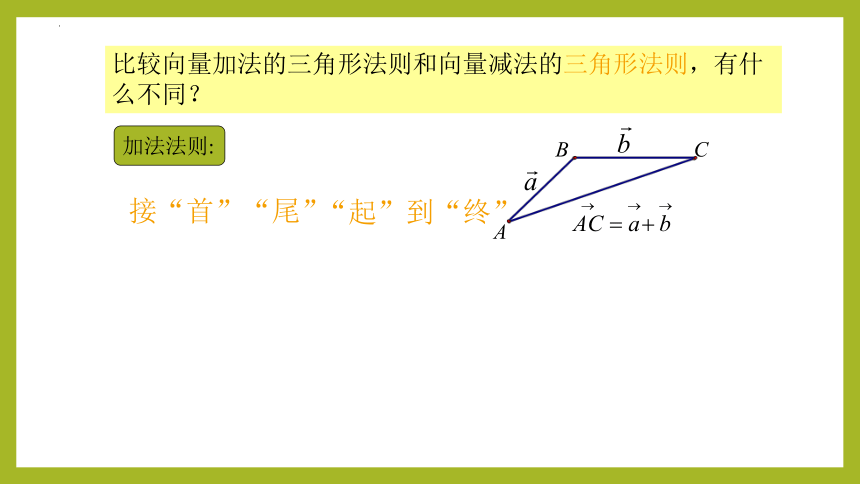
比较向量加法的三角形法则和向量减法的三角形法则,有什么不同?
A
B
C
加法法则:
接“首”“尾”
“起”到“终”
用作图的方法求两个向量的差向量
注意两点:
1.减向量与被减向量有公共起点;
2.差向量的方向指向被减向量.
归纳总结
试一试:已知向量 、 ,求作 .
解 1.在平面内任取一点A,以点A为公
共起点作向量:
A
C
B
2.以B为起点,C为终点作向量 ;
3.写出结果.
∴ 是所求的向量.
在平面内任取一点,以这点为公共起点作出这两个向量,那么它们的差向量就是以减向量的终点为起点,被减向量的终点为终点的向量,这样求两个向量的差向量的规定叫做向量减法的三角形法则.
归纳总结
如图,平行四边形OBAC中
0
B
A
C
向量的减法可以转化为向量的加法:
减去一个向量等于加上这个向量的相反向量.
即
,
b
a
BA
-
=
即
,
所以
又因为
因为
而
,
A
B
C
D
方法二:从向量减法的角度考虑
方法一:从向量加法的角度考虑
例题1 如图,试用向量 、 、
表示向量 和 .
例2、已知向量 、 、 (如图),
求作:(1)
(2)
从左到右依次运算
(1)解:
O
B
C
A
先作 、 的差
再作 、 的和
在平面内取一点O,作
∴ 是所求作的向量.
多个向量的加减
运算顺序是什么
O
B
A
C
∴ 是所求作的向量.
例2、已知向量 、 、 (如图),
求作:(1)
(2)
把向量的减法转化为加法
在平面内取一点O,作
例2、已知向量 、 、 (如图),
求作:(1)
(2)
(2)解:
O
B
C
A
在平面内取一点O,作
先作 、 的差
再作 、 的差
∴ 是所求作的向量.
例2、已知向量 、 、 (如图),
求作:(1)
(2)
O
B
C
A
∴ 是所求作的向量.
在平面内取一点O,作
把向量的减法转化为加法
1、如图,已知向量 、 ,求作
O
B
A
∴ 是所求作的向量.
还能怎样作?
课本练习
2、思考:不画图怎样直接计算:
______________
______________
______________
______________
“共”“起”点
“减”到“被”
向量减法的要领是什么?
____
3、填空
____
将向量的加减法转化成加法!
1.如图,在梯形ABCD中,AD∥BC,向量 ????????→?????????→ =( ____ )
A. ????????→ B. ????????→ C. ????????→ D. ????????→
?
【解析】解:由题意可知, ????????→?????????→ = ????????→ ,
故选:B.
?
B
随堂检测
2.下列关于向量的等式中,正确的是( ____ )
A. ????????→ + ????????→ =0 B. ????????→ + ????????→ =0
C. ????????→?????????→=????????→ D. ????????→?????????→=????????→
?
【解析】解:A、 ????????→+????????→=????→ ,
B、 ????????→+????????→=????→ ,
C、 ????????→?????????→=????????→+????????→=????????→ ,
?
C
D、 ????????→?????????→=????????→ ,
∴选项A、B、D错误,选项C正确,
故选:C.
?
3.下列向量中,与向量 ????????→ - ????????→ + ????????→ 相等的向量是( ____ )
A. ????????→ B. ????????→
C. ????????→ D. ????????→
?
【解析】解:∵ ????????→ + ????????→ = ????????→ , ????????→ - ????????→ = ????????→ + ????????→ = ????????→ ,
∴ ????????→ - ????????→ + ????????→ = ????????→ ,
?
D
故选:D.
4.如图,四边形ABCD是平行四边形,适当选取它的边或对角线作向量,记 ????????→ = ????→ ; ????????→ = ????→ ,那么图中等于 ????→ - ????→ 的向量是 .
?
【解析】解:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∴ ????????→ = ????????→ ,
∵ ????????→ = ????→ ; ????????→ = ????→ ,
∴ ????→ - ????→ = ????????→ - ????????→ = ????????→ - ????????→ = ????????→ .
?
故答案为: ????????→ .
?
5.计算 ????????→?????????→+????????→ = .
?
【解析】解: ????????→?????????→+????????→ = ????????→ + ????????→ = ????????→ .
故答案为: ????????→ .
?
6.计算: ????????→?????????→+????????→ = .
?
【解析】解: ????????→ - ????????→ + ????????→ =( ????????→ + ????????→ )- ????????→ = ????????→ - ????????→ = ????????→ .
故答案为: ????????→ .
?
7.化简: ????????→+????????→?????????→ = .
?
【解析】解:∵ ????????→+????????→?????????→ = ????????→ - ????????→ = ????????→ + ????????→ = ????????→ .
故答案为 ????????→ .
?
8.已知向量 、 、 ,求作
O
A
B
C
∴ 是所求的向量.
向量减法的两种方法
方法一:在平面内取一点,以这个点为公共起点
作出这两个向量,那么它们的差向量是
以减向量的终点为起点,被减向量的终
点为终点的向量.
方法二:减去一个向量,等于加上这个向量的相反向量
课堂小结
第 22章 四边形
22.9平面向量的减法(第1课时)
学习目标
1.通过实例理解向量加法的三角形法则及其几何意义;理解零向量的意义.
2.探究得出向量的加法满足交换律与结合律,并会用它们进行向量的运算.
3.知道向量加法的交换律与平行四边形的判定和性质定理之间的联系.
4.渗透类比的数学思想
一般来说,求不平行的两个向量的和向量时,只要把第二个向量与第一个向量首尾相接,那么以第一个向量的起点为起点、第二个向量的终点为终点的向量就是和向量.这样的规定叫做向量加法的三角形法则.
复习引入
新知探究
再作 ,则
作 ,
已知向量 ,求作
作法:
在平面内取一点A
A
B
C
数的减法是指“已知两个数的和及其中一个数,求另一个数”的运算
减法和加法的关系是什么?
减法是加法的逆运算
同样地,向量的加法也有逆运算.已知两个向量的和及其中一个向量,求另一个向量的运算叫做向量的减法
再作 ,则
作 ,
已知向量 ,求作
作法:
在平面内取一点A
,
A
B
C
请根据“向量的减法”的意义,将上述向量的加法算式改写成向量的减法算式。
观察,差向量 的起点和终点位置与被减向量 和减向量 的起点、终点的关系?
A
B
C
差向量的起点是__________的____点.
差向量的终点是__________的____点.
减向量
被减向量
终
终
已知两个向量,如何求作它们的差向量?
在平面内任取一点,以这点为公共起点作出这两个向量,那么它们的差向量是以减向量的终点为起点,被减向量的终点为终点的向量.
向量减法的三角形法则
比较向量加法的三角形法则和向量减法的三角形法则,有什么不同?
A
B
C
加法法则:
接“首”“尾”
“起”到“终”
用作图的方法求两个向量的差向量
注意两点:
1.减向量与被减向量有公共起点;
2.差向量的方向指向被减向量.
归纳总结
试一试:已知向量 、 ,求作 .
解 1.在平面内任取一点A,以点A为公
共起点作向量:
A
C
B
2.以B为起点,C为终点作向量 ;
3.写出结果.
∴ 是所求的向量.
在平面内任取一点,以这点为公共起点作出这两个向量,那么它们的差向量就是以减向量的终点为起点,被减向量的终点为终点的向量,这样求两个向量的差向量的规定叫做向量减法的三角形法则.
归纳总结
如图,平行四边形OBAC中
0
B
A
C
向量的减法可以转化为向量的加法:
减去一个向量等于加上这个向量的相反向量.
即
,
b
a
BA
-
=
即
,
所以
又因为
因为
而
,
A
B
C
D
方法二:从向量减法的角度考虑
方法一:从向量加法的角度考虑
例题1 如图,试用向量 、 、
表示向量 和 .
例2、已知向量 、 、 (如图),
求作:(1)
(2)
从左到右依次运算
(1)解:
O
B
C
A
先作 、 的差
再作 、 的和
在平面内取一点O,作
∴ 是所求作的向量.
多个向量的加减
运算顺序是什么
O
B
A
C
∴ 是所求作的向量.
例2、已知向量 、 、 (如图),
求作:(1)
(2)
把向量的减法转化为加法
在平面内取一点O,作
例2、已知向量 、 、 (如图),
求作:(1)
(2)
(2)解:
O
B
C
A
在平面内取一点O,作
先作 、 的差
再作 、 的差
∴ 是所求作的向量.
例2、已知向量 、 、 (如图),
求作:(1)
(2)
O
B
C
A
∴ 是所求作的向量.
在平面内取一点O,作
把向量的减法转化为加法
1、如图,已知向量 、 ,求作
O
B
A
∴ 是所求作的向量.
还能怎样作?
课本练习
2、思考:不画图怎样直接计算:
______________
______________
______________
______________
“共”“起”点
“减”到“被”
向量减法的要领是什么?
____
3、填空
____
将向量的加减法转化成加法!
1.如图,在梯形ABCD中,AD∥BC,向量 ????????→?????????→ =( ____ )
A. ????????→ B. ????????→ C. ????????→ D. ????????→
?
【解析】解:由题意可知, ????????→?????????→ = ????????→ ,
故选:B.
?
B
随堂检测
2.下列关于向量的等式中,正确的是( ____ )
A. ????????→ + ????????→ =0 B. ????????→ + ????????→ =0
C. ????????→?????????→=????????→ D. ????????→?????????→=????????→
?
【解析】解:A、 ????????→+????????→=????→ ,
B、 ????????→+????????→=????→ ,
C、 ????????→?????????→=????????→+????????→=????????→ ,
?
C
D、 ????????→?????????→=????????→ ,
∴选项A、B、D错误,选项C正确,
故选:C.
?
3.下列向量中,与向量 ????????→ - ????????→ + ????????→ 相等的向量是( ____ )
A. ????????→ B. ????????→
C. ????????→ D. ????????→
?
【解析】解:∵ ????????→ + ????????→ = ????????→ , ????????→ - ????????→ = ????????→ + ????????→ = ????????→ ,
∴ ????????→ - ????????→ + ????????→ = ????????→ ,
?
D
故选:D.
4.如图,四边形ABCD是平行四边形,适当选取它的边或对角线作向量,记 ????????→ = ????→ ; ????????→ = ????→ ,那么图中等于 ????→ - ????→ 的向量是 .
?
【解析】解:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∴ ????????→ = ????????→ ,
∵ ????????→ = ????→ ; ????????→ = ????→ ,
∴ ????→ - ????→ = ????????→ - ????????→ = ????????→ - ????????→ = ????????→ .
?
故答案为: ????????→ .
?
5.计算 ????????→?????????→+????????→ = .
?
【解析】解: ????????→?????????→+????????→ = ????????→ + ????????→ = ????????→ .
故答案为: ????????→ .
?
6.计算: ????????→?????????→+????????→ = .
?
【解析】解: ????????→ - ????????→ + ????????→ =( ????????→ + ????????→ )- ????????→ = ????????→ - ????????→ = ????????→ .
故答案为: ????????→ .
?
7.化简: ????????→+????????→?????????→ = .
?
【解析】解:∵ ????????→+????????→?????????→ = ????????→ - ????????→ = ????????→ + ????????→ = ????????→ .
故答案为 ????????→ .
?
8.已知向量 、 、 ,求作
O
A
B
C
∴ 是所求的向量.
向量减法的两种方法
方法一:在平面内取一点,以这个点为公共起点
作出这两个向量,那么它们的差向量是
以减向量的终点为起点,被减向量的终
点为终点的向量.
方法二:减去一个向量,等于加上这个向量的相反向量
课堂小结
