22.9平面向量的减法(第2课时)(教学课件)-八年级数学下册同步精品课堂(沪教版)
文档属性
| 名称 | 22.9平面向量的减法(第2课时)(教学课件)-八年级数学下册同步精品课堂(沪教版) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-31 00:00:00 | ||
图片预览





文档简介
2023-2024学年八年级下册数学同步精品课堂(沪教版)
第 22章 四边形
22.9平面向量的减法(第2课时)
一、向量加法的运算(作图)法则:
二、向量减法的运算(作图)法则:
1 三角形法则,(起点和终点重合)
2 多边形形法则(首尾依次相连接)
三角形法则(共起点,尾相连)
三、向量减法与加法的关系
减去一个向量等于加上这个向量的相反向量
知识回顾
向量的加法(三角形法则)
如图,已知向量a和向量b,作向量a+b.
a
b
作法:
在平面中任取
一点O,
O
a
A
b
B
a+b
过O作 OA= a
则 OB= a+b.
过A作 AB= b
首尾相接,首指向尾
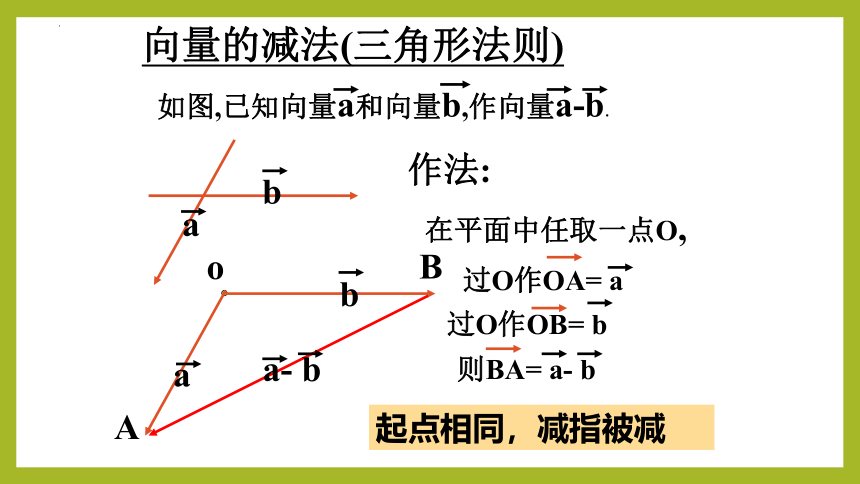
向量的减法(三角形法则)
如图,已知向量a和向量b,作向量a-b.
a
b
作法:
在平面中任取一点O,
过O作OA= a
过O作OB= b
o
a
A
b
B
则BA= a- b
a- b
起点相同,减指被减
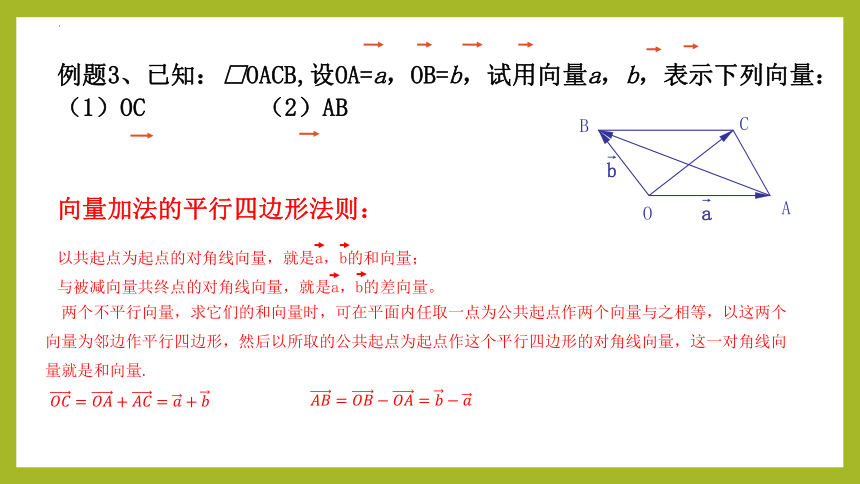
例题3、已知:□OACB,设OA=a,OB=b,试用向量a,b,表示下列向量:
(1)OC (2)AB
两个不平行向量,求它们的和向量时,可在平面内任取一点为公共起点作两个向量与之相等,以这两个向量为邻边作平行四边形,然后以所取的公共起点为起点作这个平行四边形的对角线向量,这一对角线向量就是和向量.
向量加法的平行四边形法则:
以共起点为起点的对角线向量,就是a,b的和向量;
与被减向量共终点的对角线向量,就是a,b的差向量。
????????=????????+????????=????+????
?
????????=?????????????????=?????????
?
如果 是两个不平行的向量,那么求它们的和向量时,可以在平面内任取一点为公共起点作两个向量与 相等,以这两个向量为邻边作平行四边形,然后以所取的公共起点为起点,作这个平行四边形的对角线向量,则这一对角线向量就是 的和向量.——这个规定叫做向量加法的平行四边形法则.
另外一个对角线向量即是 的差向量,这个差向量与被减向量共终点.
向量加法的平行四边形法则
例题4、已知:向量a、b,用向量加法的平行四边形法则
作向量a+b,再作向量a-b。
b
a
向量的加减法(平行四边形法则)
如图,已知向量a和向量b,作向量a+b,a-b.
a
作法:
在平面中任取一点O,
过O作OA= a
过O作OB= b
O
a
A
b
B
b
以OA,OB为边作
平行四边形
则对角线OC= a+b
a+b
C
则对角线BA= a-b
例题5、在一段宽阔的河道中,河水以40米/分的速度向东流去.一艘小艇顺流航行到A处,然后沿着北偏东10°方向以12千米/时的速度驶往北岸,请用作图方法指出小艇实际航行的方向.
北岸
南岸
河 道
A
G
M
m
n
N
100
课本练习
1.如图,四边形ABCD和四边形ACDE都是平行四边形,
(1)填空: ????????→+????????→ = ; ????????→?????????→+????????→ = ;
(2)求作: ????????→+????????→ .
?
【解析】解:(1)填空: ????????→+????????→ = ????????→ ; ????????→?????????→+????????→ = ????????→ +????????→ = ????→ ;
(2) ????????→+????????→ = ????????→+????????→=????????→ ,或 ????????→+????????→ = ????????→ .
?
随堂检测
所画图形如下所示:
_______
2.如图,点E在平行四边形ABCD的对角线BD上.
(1)填空: ????????→+????????→ = ; ????????→?????????→ = ;
(2)求作: ????????→+????????→ .(不写作法,保留作图痕迹,写出结果).
?
【解析】解:(1)∵ ????????→ = ????????→ ,- ????????→ = ????????→ ,
∴ ????????→+????????→ = ????????→ + ????????→ = ????????→ ; ????????→?????????→ = ????????→ + ????????→ = ????????→ ;
(2)所作图形如下:
?
????????→ 即为所求向量.
?
3.如图,在四边形ABCD中.
(1)用图中的向量表示: ????????→ + ????????→ + ????????→ = ;(2)用图中的向量表示: ????????→ - ????????→ = ;
(3)在作图区内求作并写结论: ????????→ + ????????→ .
_____
?
【解析】解:(1)用图中的向量表示: ????????→ + ????????→ + ????????→ = ????????→ ;
故答案为: ????????→ .
(2)用图中的向量表示: ????????→ - ????????→ = ????????→ ;
故答案为: ????????→ .
(3)在作图区内求作并写结论: ????????→ + ????????→ = ????????→ + ????????→ = ????????→ ,
????????→ 即为所求,
?
4.已知:如图,平行四边形ABCD,E、F、G、H分别是AB、BC、CD、AD上的点,且AE=CG,BF=DH.
(1)写出与 ????????→ 相反的向量;
(2)写出与 ????????→ 平行的向量;
(3)在图中求作 ????????→ - ????????→ .(不要求写出作法,只需写出结论即可.)
?
【解析】解:(1)与 ????????→ 相反的向量为 ????????→ 、 ????????→ ;
?
(2)与 ????????→ 平行的向量有 ????????→ 、 ????????→ 、 ????????→ ;
(3)图中向量 ????????→ 即为所求.
_____
?
一、向量加法的运算(作图)法则:
二、向量减法的运算(作图)法则:
1、三角形法则,(起点和终点重合)
2、多边形形法则(首尾依次相连接)
1、三角形法则(共起点,尾相连)
3、平行四边形法则(共起点,做平行四边形)
2、平行四边形法则(共起点,做平行四边形)
以共起点为起点的对角线向量,就是a,b的和向量;
与被减向量共终点的对角线向量,就是a,b的差向量。
课堂小结
第 22章 四边形
22.9平面向量的减法(第2课时)
一、向量加法的运算(作图)法则:
二、向量减法的运算(作图)法则:
1 三角形法则,(起点和终点重合)
2 多边形形法则(首尾依次相连接)
三角形法则(共起点,尾相连)
三、向量减法与加法的关系
减去一个向量等于加上这个向量的相反向量
知识回顾
向量的加法(三角形法则)
如图,已知向量a和向量b,作向量a+b.
a
b
作法:
在平面中任取
一点O,
O
a
A
b
B
a+b
过O作 OA= a
则 OB= a+b.
过A作 AB= b
首尾相接,首指向尾
向量的减法(三角形法则)
如图,已知向量a和向量b,作向量a-b.
a
b
作法:
在平面中任取一点O,
过O作OA= a
过O作OB= b
o
a
A
b
B
则BA= a- b
a- b
起点相同,减指被减
例题3、已知:□OACB,设OA=a,OB=b,试用向量a,b,表示下列向量:
(1)OC (2)AB
两个不平行向量,求它们的和向量时,可在平面内任取一点为公共起点作两个向量与之相等,以这两个向量为邻边作平行四边形,然后以所取的公共起点为起点作这个平行四边形的对角线向量,这一对角线向量就是和向量.
向量加法的平行四边形法则:
以共起点为起点的对角线向量,就是a,b的和向量;
与被减向量共终点的对角线向量,就是a,b的差向量。
????????=????????+????????=????+????
?
????????=?????????????????=?????????
?
如果 是两个不平行的向量,那么求它们的和向量时,可以在平面内任取一点为公共起点作两个向量与 相等,以这两个向量为邻边作平行四边形,然后以所取的公共起点为起点,作这个平行四边形的对角线向量,则这一对角线向量就是 的和向量.——这个规定叫做向量加法的平行四边形法则.
另外一个对角线向量即是 的差向量,这个差向量与被减向量共终点.
向量加法的平行四边形法则
例题4、已知:向量a、b,用向量加法的平行四边形法则
作向量a+b,再作向量a-b。
b
a
向量的加减法(平行四边形法则)
如图,已知向量a和向量b,作向量a+b,a-b.
a
作法:
在平面中任取一点O,
过O作OA= a
过O作OB= b
O
a
A
b
B
b
以OA,OB为边作
平行四边形
则对角线OC= a+b
a+b
C
则对角线BA= a-b
例题5、在一段宽阔的河道中,河水以40米/分的速度向东流去.一艘小艇顺流航行到A处,然后沿着北偏东10°方向以12千米/时的速度驶往北岸,请用作图方法指出小艇实际航行的方向.
北岸
南岸
河 道
A
G
M
m
n
N
100
课本练习
1.如图,四边形ABCD和四边形ACDE都是平行四边形,
(1)填空: ????????→+????????→ = ; ????????→?????????→+????????→ = ;
(2)求作: ????????→+????????→ .
?
【解析】解:(1)填空: ????????→+????????→ = ????????→ ; ????????→?????????→+????????→ = ????????→ +????????→ = ????→ ;
(2) ????????→+????????→ = ????????→+????????→=????????→ ,或 ????????→+????????→ = ????????→ .
?
随堂检测
所画图形如下所示:
_______
2.如图,点E在平行四边形ABCD的对角线BD上.
(1)填空: ????????→+????????→ = ; ????????→?????????→ = ;
(2)求作: ????????→+????????→ .(不写作法,保留作图痕迹,写出结果).
?
【解析】解:(1)∵ ????????→ = ????????→ ,- ????????→ = ????????→ ,
∴ ????????→+????????→ = ????????→ + ????????→ = ????????→ ; ????????→?????????→ = ????????→ + ????????→ = ????????→ ;
(2)所作图形如下:
?
????????→ 即为所求向量.
?
3.如图,在四边形ABCD中.
(1)用图中的向量表示: ????????→ + ????????→ + ????????→ = ;(2)用图中的向量表示: ????????→ - ????????→ = ;
(3)在作图区内求作并写结论: ????????→ + ????????→ .
_____
?
【解析】解:(1)用图中的向量表示: ????????→ + ????????→ + ????????→ = ????????→ ;
故答案为: ????????→ .
(2)用图中的向量表示: ????????→ - ????????→ = ????????→ ;
故答案为: ????????→ .
(3)在作图区内求作并写结论: ????????→ + ????????→ = ????????→ + ????????→ = ????????→ ,
????????→ 即为所求,
?
4.已知:如图,平行四边形ABCD,E、F、G、H分别是AB、BC、CD、AD上的点,且AE=CG,BF=DH.
(1)写出与 ????????→ 相反的向量;
(2)写出与 ????????→ 平行的向量;
(3)在图中求作 ????????→ - ????????→ .(不要求写出作法,只需写出结论即可.)
?
【解析】解:(1)与 ????????→ 相反的向量为 ????????→ 、 ????????→ ;
?
(2)与 ????????→ 平行的向量有 ????????→ 、 ????????→ 、 ????????→ ;
(3)图中向量 ????????→ 即为所求.
_____
?
一、向量加法的运算(作图)法则:
二、向量减法的运算(作图)法则:
1、三角形法则,(起点和终点重合)
2、多边形形法则(首尾依次相连接)
1、三角形法则(共起点,尾相连)
3、平行四边形法则(共起点,做平行四边形)
2、平行四边形法则(共起点,做平行四边形)
以共起点为起点的对角线向量,就是a,b的和向量;
与被减向量共终点的对角线向量,就是a,b的差向量。
课堂小结
