专题02代数方程(考点串讲)-八年级数学下学期期末考点大串讲(沪教版)
文档属性
| 名称 | 专题02代数方程(考点串讲)-八年级数学下学期期末考点大串讲(沪教版) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-31 14:05:59 | ||
图片预览










文档简介
(共42张PPT)
八年级沪教版数学下册期末考点大串讲
串讲02 代数方程
01
02
04
03
目
录
易错易混
题型剖析
考点透视
押题预测
五大易错易混经典例题+针对训练
5道期末真题对应考点练
八大重难点题型典例剖析
八大常考点:知识梳理+针对训练
代数方程
整式方程
有理方程
无理方程
列方程(组)解应用题
分式方程
一元方程
多元方程组
二元一次方程组
一次方程
高次方程
二次方程
二元二次方程组
考点透视
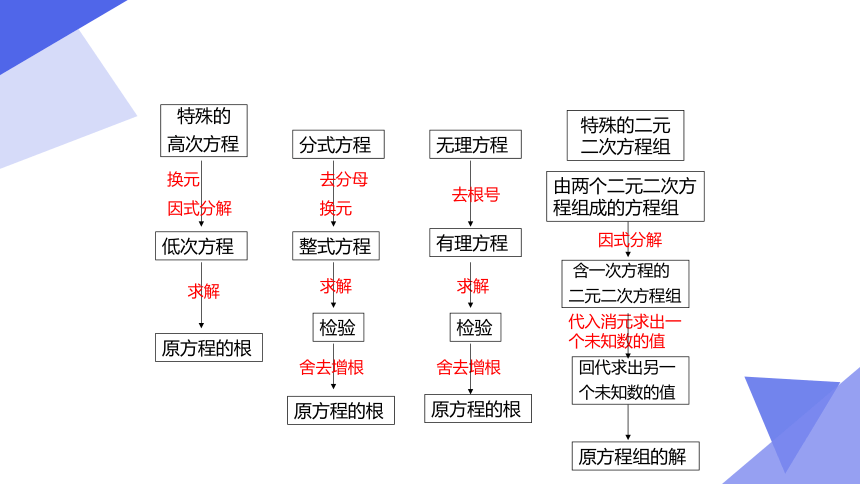
化归思想与方法
特殊的
高次方程
低次方程
原方程的根
换元
因式分解
分式方程
整式方程
检验
原方程的根
去分母
换元
求解
求解
舍去增根
无理方程
有理方程
检验
原方程的根
去根号
求解
舍去增根
由两个二元二次方程组成的方程组
含一次方程的
二元二次方程组
回代求出另一
个未知数的值
原方程组的解
因式分解
代入消元求出一个未知数的值
特殊的二元二次方程组
1、字母系数方程的讨论
关于ax=b的解有三种情况
关于ax2=m的解的情况
题型剖析
针对练习1.关于x方程a(x-1)=1(a≠0)的解是 .
【解析】解:a(x-1)=1, ,
∴ ;
故答案为 .
针对练习2.二项方程2x3+16=0在实数范围内的解是 ______ .
【解析】解:∵2x3+16=0,
∴2x3=-16,
∴x3=-8,
则x= =-2,
故答案为:x=-2.
x=-2
使最简公分母为零
3、分式方程的解法
解分式方程的基本思路是:
通过“去分母”将分式方程转化为整式方程
解分式方程的一般步骤:
分式方程
同乘以最简公分母
整式方程
检验
舍去
写出方程的根
使最简公分母不为零
去分母的关键是确定最简公分母,
在转化过程中要注意不要漏乘,不忘检验。
针对练习:解方程: .
【解析】解:去分母得:(x+2)2-16=x-2,
整理得:x2+4x+4-16=x-2,即x2+3x-10=0,
分解因式得:(x-2)(x+5)=0,
解得:x=2或x=-5,
检验:当x=2时,(x+2)(x-2)=0,
当x=-5时,(x+2)(x-2)≠0,
∴x=2是增根,分式方程的解为x=-5.
4、用换元法解分式方程
1.原方程可看作某一分式的二次方程.
2.原方程含有未知数的几个分式有互为倒数的关系.
特别注意:换元法解分式方程需要验根两次
第1次检验y的方程是否有增根
第2次是回代后的关于x两个方程是否有增根
题型一:直接换元
例题1
解方程:
题型二:倒数换元
例题2
解方程:
题型三:配方换元
例题3
解方程:
所以,原方程的根是
例题4
解方程组:
题型四:换元法解分式方程组
分析:
观察方程组中所含的分式,它们的分母是或联想“换元”的方法,如果把看作两个不同的“整体”,分别用代替,即设= ,转化为二元一次方程组进行求解.
【解析】解:设 =a, =b,
∴原方程化为: ,
解得: ,
∴ =1, =2,
针对练习
∴ ,
解得: ,
经检验: 是原方程组的解.
5、无理方程的解法
解无理方程的一般步骤:
是
开始
去根号
解有理方程
检验
具体方法:平方法
体现的数学思想:化归思想
无理方程有理化
结束
检验
写出原方程的根
舍去
不是
观察分析的方法也是解无理方程的一种好方法
1.解方程:
【解析】解:原方程两边同时平方得:3x+4=x2,
整理得:x2-3x-4=0,
因式分解得:(x+1)(x-4)=0,
解得:x1=-1,x2=4,
∵3x+4≥0且x≥0,
∴x≥0,
则x=-1应舍去,
故原方程的解为:x=4.
针对练习
2. .
【解析】解:∵ ,
∴ ,
∴ ,
∴ ,
∴x2+4x+4=16x-16,
∴x2-12x+20=0,
∴(x-2)(x-10)=0
解得x1=2,x2=10.
6、有关增根的问题
增根产生的原因:
在解分式方程或无理方程时,将方程转化成整式方程或
有理方程时,扩大了未知数的取值范围,从而产生了增根
如何检验是否增根
将解分式方程转化成整式方程的根代入最简公分母,若使最简公分母为零的根为原方程的增根,否则为原方程的根
将解无理方程转化成有理方程的根代入原方程的左右两边,若使方程左右两边的值不相等的根为增根,否则为方程的根
针对练习:若分式方程 有增根x=-1,求k的值.
【解析】解:两边都乘以x(x-1)(x+1),得:(k-1)x-(x+1)=(x+1)(k-5),
∵方程有增根x=-1,
∴代入整式方程,得:-(k-1)=0,
解得:k=1.
7、二元二次方程(组)
二·一型二元二次方程组
代入消元法、因式分解降次法和利用根与系数关系
二·二型二元二次方程组
因式分解法
针对练习1:解方程组: .
【解析】解: ,
法一、由②,得x=1-y③,
把③代入①,得(1-y)2+4(1-y)×y+4y2=9,
整理,得y2+2y-8=0.
∴(y+4)(y-2)=0.
∴y1=-4,y2=2.
把y1=-4,y2=2分别代入③,得x1=5,x2=-1.
∴原方程的解为 , .
法二、由①,得(x+2y)2=9,
∴x+2y=3或x+2y=-3.
于是原方程组可化为 或 .
解这两个方程组,得 , .
所以原方程组的解为: , .
针对练习2:解方程组: .
【解析】解:由①,得x(x+y)=0,
∴x=0或者x+y=0.
由②,得(x2-2xy+y2)-1=0,
∴(x-y)2-1=0.
∴(x-y+1)(x-y-1)=0.
∴x-y+1=0或者x-y-1=0.
所以原方程组可变形为 或 或 或
解得 , , , .
所以原方程组的解为 , , , .
8、列方程(组)解应用题
审题
设元
找等量
关系
列方程
解方程
检验
作答
①检验是否是所列方程的解
②检验是否符合实际意义
增长率问题,工程问题,行程问题……
针对练习1:甲乙两队要限期完成某工程,甲队独做提前2天完成,乙队独做要延期5天,现在两队合作3天后余下的由乙队独做,正好如期完工,设工程期限为x天,那么可列方程为( ____ )
A. B.
C. D.
【解析】解:设工作总量为1,工程期限为x天,
C
那么甲工程队的工作效率为 ,乙工程队的工作效率为 .
根据题意,所列方程为 ,
化简得 .
故选:C.
针对练习2:某商店以每件20元的价格购进一批文具盒,然后以每只30元的价格出售,结果每周可以售出400只,后来经过市场调查发现:当单价每提高0.5元,每周销售量会少10只,如果某一周销售这种文具盒的总利润是4500元,那么这周每只文具盒的售价为多少元?
【解析】解:设这周每只文具盒的售价为x元,
由题意知:(x-20) ,
整理得x2-70x+1225=0,
解得x1=x2=35,
即这周每只文具盒的售价为35元.
针对练习3:近年来,我国逐步完善养老金保险制度.甲、乙两人计划分别缴纳养老保险金12万元和8万元,虽然甲计划每年比乙计划每年多缴纳养老保险金0.1万元,但是甲计划缴纳养老保险金的年数还是比乙要多4年,已知甲、乙两人计划缴纳养老保险金的年数都不超过20年,求甲计划每年缴纳养老保险金多少万元?
【解析】解:设甲计划每年缴纳养老保险金x万元,则乙计划每年缴纳养老保险金(x-0.1)万元,
根据题意得: - =4,
整理得:10x2-11x+3=0,
解得:x1=0.5,x2=0.6,
经检验,x1=0.5,x2=0.6均为所列方程的解,x1=0.5不符合题意,舍去,x2=0.6符合题意.
答:甲计划每年缴纳养老保险金0.6万元.
针对练习4:A、B两地相距360千米,一辆汽车准备从A地开往B地,但由于任务紧急,现在实际行驶的速度每小时比原计划快20千米,所以提前3小时到达B地.求汽车原计划的速度.
【解析】解:设汽车原计划的速度为x千米/时,则汽车实际行驶的速度为(x+20)千米/时,
根据题意得: - =3,
整理得:x2+20x-2400=0,
解得:x1=40,x2=-60,
经检验,x1=40,x2=-60均为所列方程的解,x1=40符合题意,x2=-60不符合题意,舍去.
答:汽车原计划的速度为40千米/时.
1.下列各题下列各题解方程的过程错在哪里? 的
(1)解关于x的方程:
bx2+1=2(b≠0)
解:bx2=1
x2= —
∴x=±
b
1
需要讨论
易错易混
(2)解方程:
x+1
2x
——
- —
1
x
=2
甲同学:方程左右两边同乘以
x(x+1)得
2 x -x-1= 2
x= 3
检验:当x= 3时,x(x+1) ≠0
∴原方程的根为x= 3
常数也要乘以公分母
注意变号
乙同学:方程左右两边同乘以 x(x+1)得
2x -x+1=2x(x+1)
2x2+x-1=0
解得x1= — ,x2=-1
1
2
经检验:x=-1是增根,舍去
∴原方程的根为
x= —
2
1
2.下列各题解方程的过程错在哪里?
(3)解方程:
解:原方程可化为
方程两边同乘以3x(x-1)得
3x-(x-1)=x
解得x= ﹣1
检验:当x=﹣1时,3x(x﹣1) ≠0
∴原方程的根为x=﹣1
代入原方程的最简公分母进行检验
3.下列各题解方程的过程错在哪里?
(4)解方程:
解:原方程化为
方程左右两边同时平方得
x2-5x + 6 = 2
x2-5x+4=0
∴x1=1,x2=4
(x-1)(x-4)=0
∴原方程的根为x1=1,x2=4
(x-2)(x-3)
2
=
检验:当 时,原方程左边=右边
x1=1,x2=4
要代入原无理方程进行检验
4.下列各题解方程的过程错在哪里?
(5)解方程组:
5x2-y2=11
2x-y=1
①
②
解:由②得y=2x-1③
将③代入①得5x2-(2x-1)2=11
即x2+4x-12=0
解得x1=2,x2=﹣6
把x=2代入①得y=±3
把x=﹣6代入①得y=±13
∴原方程组的解为
x1=2
y1=3
x2=2
y2=﹣3
x1=﹣6
y1=13
x1=﹣6
y1=﹣13
回代二元一次方程求另一个未知数
5.下列各题解方程的过程错在哪里?
1.(2023春·浦东新区校级期末)下列方程中,有实数根的方程是( ____ )
A.2x4+1=0 B.x3+1=0
C. +3=0 D. =
【解析】解:A、整理得:x4=- ,故次方程无解;
B、整理得x3=-1,解得:x=-1,符合题意;
C、整理得 =-3,无解,不符合题意;
D、去分母后得x=1,代入最简公分母x-1=0,故次方程无实数根,
故选:B.
B
押题预测
2.(2023春·长宁区期末)方程x3-27=0的根是 _____ .
【解析】解:x3-27=0,
x3=27,
x= =3,
故答案为:x=3.
x=3
3.(2023春·长宁区校级期末)解方程组: .
【解析】解: ,
由①,得(x-y)(x-2y)=0,
即x-y=0或x-2y=0,
把这两个方程与②组成方程组得: , ,
解得: , ,故方程组的解为: ,
4.(2023春·浦东新区校级期末)解方程: - =1
【解析】解: = +1
x+2=x+2 +1
1=2
,
经检验,x= 是原方程的解.
5.(2023春·徐汇区期末)某商店以2400元购进某种盒装茶叶,第一个月每盒按进价增加20%作为售价,售出50盒,第二个月每盒以低于进价5元作为售价,售完余下的茶叶.在整个买卖过程中盈利350元,求每盒茶叶的进价.
【解析】解:设每盒茶叶的进价为x元.
50×x(1+20%)+(x-5)×( -50)-2400=350.
解得:x=40或x=-30,
经检验:x=40或x=-30都是原方程的解,但x=-30不合题意,应舍去.
答:每盒茶叶的进价为40元.
八年级沪教版数学下册期末考点大串讲
串讲02 代数方程
01
02
04
03
目
录
易错易混
题型剖析
考点透视
押题预测
五大易错易混经典例题+针对训练
5道期末真题对应考点练
八大重难点题型典例剖析
八大常考点:知识梳理+针对训练
代数方程
整式方程
有理方程
无理方程
列方程(组)解应用题
分式方程
一元方程
多元方程组
二元一次方程组
一次方程
高次方程
二次方程
二元二次方程组
考点透视
化归思想与方法
特殊的
高次方程
低次方程
原方程的根
换元
因式分解
分式方程
整式方程
检验
原方程的根
去分母
换元
求解
求解
舍去增根
无理方程
有理方程
检验
原方程的根
去根号
求解
舍去增根
由两个二元二次方程组成的方程组
含一次方程的
二元二次方程组
回代求出另一
个未知数的值
原方程组的解
因式分解
代入消元求出一个未知数的值
特殊的二元二次方程组
1、字母系数方程的讨论
关于ax=b的解有三种情况
关于ax2=m的解的情况
题型剖析
针对练习1.关于x方程a(x-1)=1(a≠0)的解是 .
【解析】解:a(x-1)=1, ,
∴ ;
故答案为 .
针对练习2.二项方程2x3+16=0在实数范围内的解是 ______ .
【解析】解:∵2x3+16=0,
∴2x3=-16,
∴x3=-8,
则x= =-2,
故答案为:x=-2.
x=-2
使最简公分母为零
3、分式方程的解法
解分式方程的基本思路是:
通过“去分母”将分式方程转化为整式方程
解分式方程的一般步骤:
分式方程
同乘以最简公分母
整式方程
检验
舍去
写出方程的根
使最简公分母不为零
去分母的关键是确定最简公分母,
在转化过程中要注意不要漏乘,不忘检验。
针对练习:解方程: .
【解析】解:去分母得:(x+2)2-16=x-2,
整理得:x2+4x+4-16=x-2,即x2+3x-10=0,
分解因式得:(x-2)(x+5)=0,
解得:x=2或x=-5,
检验:当x=2时,(x+2)(x-2)=0,
当x=-5时,(x+2)(x-2)≠0,
∴x=2是增根,分式方程的解为x=-5.
4、用换元法解分式方程
1.原方程可看作某一分式的二次方程.
2.原方程含有未知数的几个分式有互为倒数的关系.
特别注意:换元法解分式方程需要验根两次
第1次检验y的方程是否有增根
第2次是回代后的关于x两个方程是否有增根
题型一:直接换元
例题1
解方程:
题型二:倒数换元
例题2
解方程:
题型三:配方换元
例题3
解方程:
所以,原方程的根是
例题4
解方程组:
题型四:换元法解分式方程组
分析:
观察方程组中所含的分式,它们的分母是或联想“换元”的方法,如果把看作两个不同的“整体”,分别用代替,即设= ,转化为二元一次方程组进行求解.
【解析】解:设 =a, =b,
∴原方程化为: ,
解得: ,
∴ =1, =2,
针对练习
∴ ,
解得: ,
经检验: 是原方程组的解.
5、无理方程的解法
解无理方程的一般步骤:
是
开始
去根号
解有理方程
检验
具体方法:平方法
体现的数学思想:化归思想
无理方程有理化
结束
检验
写出原方程的根
舍去
不是
观察分析的方法也是解无理方程的一种好方法
1.解方程:
【解析】解:原方程两边同时平方得:3x+4=x2,
整理得:x2-3x-4=0,
因式分解得:(x+1)(x-4)=0,
解得:x1=-1,x2=4,
∵3x+4≥0且x≥0,
∴x≥0,
则x=-1应舍去,
故原方程的解为:x=4.
针对练习
2. .
【解析】解:∵ ,
∴ ,
∴ ,
∴ ,
∴x2+4x+4=16x-16,
∴x2-12x+20=0,
∴(x-2)(x-10)=0
解得x1=2,x2=10.
6、有关增根的问题
增根产生的原因:
在解分式方程或无理方程时,将方程转化成整式方程或
有理方程时,扩大了未知数的取值范围,从而产生了增根
如何检验是否增根
将解分式方程转化成整式方程的根代入最简公分母,若使最简公分母为零的根为原方程的增根,否则为原方程的根
将解无理方程转化成有理方程的根代入原方程的左右两边,若使方程左右两边的值不相等的根为增根,否则为方程的根
针对练习:若分式方程 有增根x=-1,求k的值.
【解析】解:两边都乘以x(x-1)(x+1),得:(k-1)x-(x+1)=(x+1)(k-5),
∵方程有增根x=-1,
∴代入整式方程,得:-(k-1)=0,
解得:k=1.
7、二元二次方程(组)
二·一型二元二次方程组
代入消元法、因式分解降次法和利用根与系数关系
二·二型二元二次方程组
因式分解法
针对练习1:解方程组: .
【解析】解: ,
法一、由②,得x=1-y③,
把③代入①,得(1-y)2+4(1-y)×y+4y2=9,
整理,得y2+2y-8=0.
∴(y+4)(y-2)=0.
∴y1=-4,y2=2.
把y1=-4,y2=2分别代入③,得x1=5,x2=-1.
∴原方程的解为 , .
法二、由①,得(x+2y)2=9,
∴x+2y=3或x+2y=-3.
于是原方程组可化为 或 .
解这两个方程组,得 , .
所以原方程组的解为: , .
针对练习2:解方程组: .
【解析】解:由①,得x(x+y)=0,
∴x=0或者x+y=0.
由②,得(x2-2xy+y2)-1=0,
∴(x-y)2-1=0.
∴(x-y+1)(x-y-1)=0.
∴x-y+1=0或者x-y-1=0.
所以原方程组可变形为 或 或 或
解得 , , , .
所以原方程组的解为 , , , .
8、列方程(组)解应用题
审题
设元
找等量
关系
列方程
解方程
检验
作答
①检验是否是所列方程的解
②检验是否符合实际意义
增长率问题,工程问题,行程问题……
针对练习1:甲乙两队要限期完成某工程,甲队独做提前2天完成,乙队独做要延期5天,现在两队合作3天后余下的由乙队独做,正好如期完工,设工程期限为x天,那么可列方程为( ____ )
A. B.
C. D.
【解析】解:设工作总量为1,工程期限为x天,
C
那么甲工程队的工作效率为 ,乙工程队的工作效率为 .
根据题意,所列方程为 ,
化简得 .
故选:C.
针对练习2:某商店以每件20元的价格购进一批文具盒,然后以每只30元的价格出售,结果每周可以售出400只,后来经过市场调查发现:当单价每提高0.5元,每周销售量会少10只,如果某一周销售这种文具盒的总利润是4500元,那么这周每只文具盒的售价为多少元?
【解析】解:设这周每只文具盒的售价为x元,
由题意知:(x-20) ,
整理得x2-70x+1225=0,
解得x1=x2=35,
即这周每只文具盒的售价为35元.
针对练习3:近年来,我国逐步完善养老金保险制度.甲、乙两人计划分别缴纳养老保险金12万元和8万元,虽然甲计划每年比乙计划每年多缴纳养老保险金0.1万元,但是甲计划缴纳养老保险金的年数还是比乙要多4年,已知甲、乙两人计划缴纳养老保险金的年数都不超过20年,求甲计划每年缴纳养老保险金多少万元?
【解析】解:设甲计划每年缴纳养老保险金x万元,则乙计划每年缴纳养老保险金(x-0.1)万元,
根据题意得: - =4,
整理得:10x2-11x+3=0,
解得:x1=0.5,x2=0.6,
经检验,x1=0.5,x2=0.6均为所列方程的解,x1=0.5不符合题意,舍去,x2=0.6符合题意.
答:甲计划每年缴纳养老保险金0.6万元.
针对练习4:A、B两地相距360千米,一辆汽车准备从A地开往B地,但由于任务紧急,现在实际行驶的速度每小时比原计划快20千米,所以提前3小时到达B地.求汽车原计划的速度.
【解析】解:设汽车原计划的速度为x千米/时,则汽车实际行驶的速度为(x+20)千米/时,
根据题意得: - =3,
整理得:x2+20x-2400=0,
解得:x1=40,x2=-60,
经检验,x1=40,x2=-60均为所列方程的解,x1=40符合题意,x2=-60不符合题意,舍去.
答:汽车原计划的速度为40千米/时.
1.下列各题下列各题解方程的过程错在哪里? 的
(1)解关于x的方程:
bx2+1=2(b≠0)
解:bx2=1
x2= —
∴x=±
b
1
需要讨论
易错易混
(2)解方程:
x+1
2x
——
- —
1
x
=2
甲同学:方程左右两边同乘以
x(x+1)得
2 x -x-1= 2
x= 3
检验:当x= 3时,x(x+1) ≠0
∴原方程的根为x= 3
常数也要乘以公分母
注意变号
乙同学:方程左右两边同乘以 x(x+1)得
2x -x+1=2x(x+1)
2x2+x-1=0
解得x1= — ,x2=-1
1
2
经检验:x=-1是增根,舍去
∴原方程的根为
x= —
2
1
2.下列各题解方程的过程错在哪里?
(3)解方程:
解:原方程可化为
方程两边同乘以3x(x-1)得
3x-(x-1)=x
解得x= ﹣1
检验:当x=﹣1时,3x(x﹣1) ≠0
∴原方程的根为x=﹣1
代入原方程的最简公分母进行检验
3.下列各题解方程的过程错在哪里?
(4)解方程:
解:原方程化为
方程左右两边同时平方得
x2-5x + 6 = 2
x2-5x+4=0
∴x1=1,x2=4
(x-1)(x-4)=0
∴原方程的根为x1=1,x2=4
(x-2)(x-3)
2
=
检验:当 时,原方程左边=右边
x1=1,x2=4
要代入原无理方程进行检验
4.下列各题解方程的过程错在哪里?
(5)解方程组:
5x2-y2=11
2x-y=1
①
②
解:由②得y=2x-1③
将③代入①得5x2-(2x-1)2=11
即x2+4x-12=0
解得x1=2,x2=﹣6
把x=2代入①得y=±3
把x=﹣6代入①得y=±13
∴原方程组的解为
x1=2
y1=3
x2=2
y2=﹣3
x1=﹣6
y1=13
x1=﹣6
y1=﹣13
回代二元一次方程求另一个未知数
5.下列各题解方程的过程错在哪里?
1.(2023春·浦东新区校级期末)下列方程中,有实数根的方程是( ____ )
A.2x4+1=0 B.x3+1=0
C. +3=0 D. =
【解析】解:A、整理得:x4=- ,故次方程无解;
B、整理得x3=-1,解得:x=-1,符合题意;
C、整理得 =-3,无解,不符合题意;
D、去分母后得x=1,代入最简公分母x-1=0,故次方程无实数根,
故选:B.
B
押题预测
2.(2023春·长宁区期末)方程x3-27=0的根是 _____ .
【解析】解:x3-27=0,
x3=27,
x= =3,
故答案为:x=3.
x=3
3.(2023春·长宁区校级期末)解方程组: .
【解析】解: ,
由①,得(x-y)(x-2y)=0,
即x-y=0或x-2y=0,
把这两个方程与②组成方程组得: , ,
解得: , ,故方程组的解为: ,
4.(2023春·浦东新区校级期末)解方程: - =1
【解析】解: = +1
x+2=x+2 +1
1=2
,
经检验,x= 是原方程的解.
5.(2023春·徐汇区期末)某商店以2400元购进某种盒装茶叶,第一个月每盒按进价增加20%作为售价,售出50盒,第二个月每盒以低于进价5元作为售价,售完余下的茶叶.在整个买卖过程中盈利350元,求每盒茶叶的进价.
【解析】解:设每盒茶叶的进价为x元.
50×x(1+20%)+(x-5)×( -50)-2400=350.
解得:x=40或x=-30,
经检验:x=40或x=-30都是原方程的解,但x=-30不合题意,应舍去.
答:每盒茶叶的进价为40元.
同课章节目录
