专题03三角形(考点串讲)-七年级数学下学期期末考点大串讲(沪教版)
文档属性
| 名称 | 专题03三角形(考点串讲)-七年级数学下学期期末考点大串讲(沪教版) |
|
|
| 格式 | pptx | ||
| 文件大小 | 3.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-27 00:00:00 | ||
图片预览






文档简介
七年级沪教版数学下册期末考点大串讲
串讲03 三角形
01
02
04
03
目
录
易错易混
题型剖析
考点透视
押题预测
易错易混分析
7道期末真题对应考点练
四大重难点题型典例剖析+强化训练+两类期末重难点突破
四大常考点:知识梳理+考点分类训练
考点透视
C
D
C
不稳定性
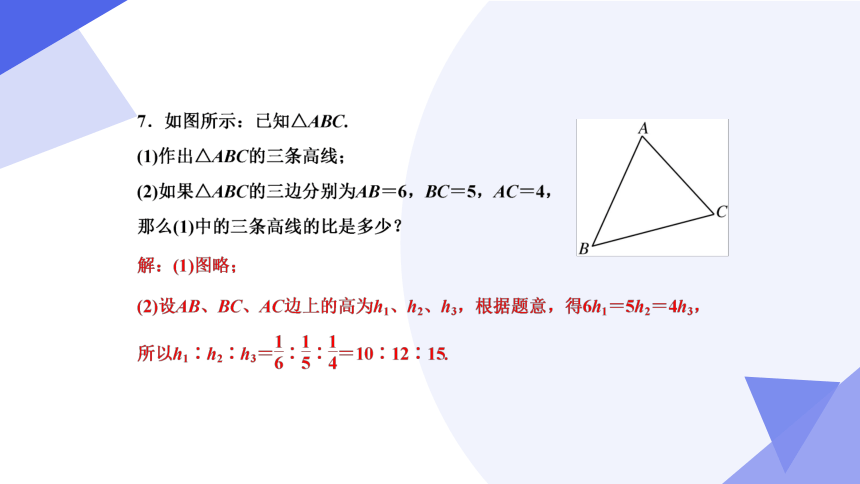
6
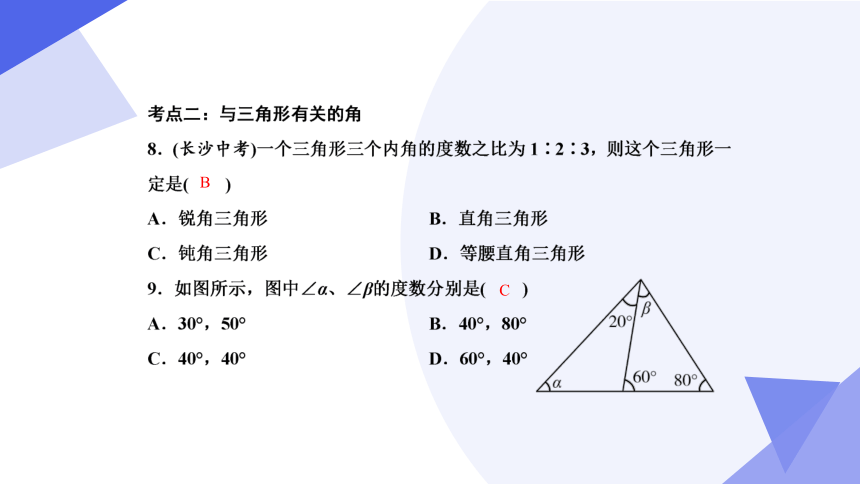
B
C
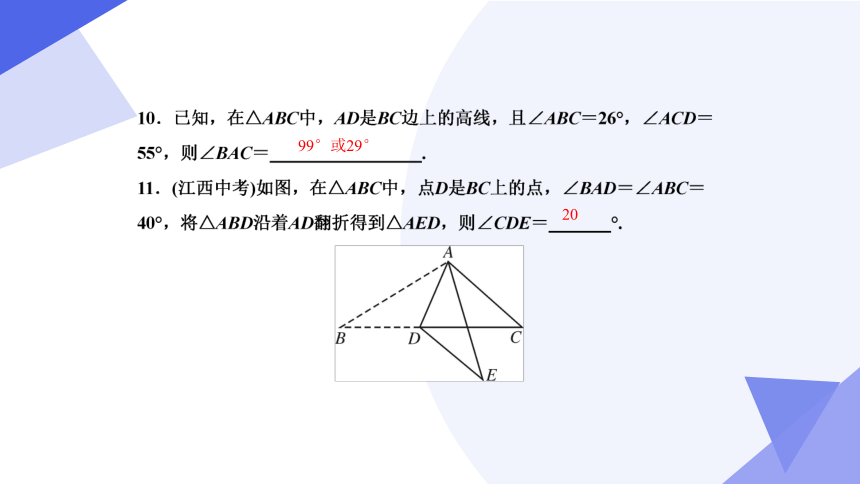
99°或29°
20
C
A
B
B
期末重难点突破一:运用数学模型求相关夹角问题
期末重难点突破二:巧作辅助线构造全等三角形
1.(2023春·黄浦区期末 )现有2cm,3cm,5cm,6cm长的四根木棒,任选其中的三根组成三角形,那么可以组成三角形的个数有( ____ )
A.1个 B.2个 C.3个 D.4个
【解析】解:四条木棒的所有组合:2,3,5和2,3,6和2,5,6和3,5,6;
只有2,5,6和3,5,6能组成三角形.
故选:B.
B
押题预测
2.(2023春·黄浦区期末)如图,点P是AB上任一点,∠ABC=∠ABD,从下列各条件中补充一个条件,不一定能推出△APC≌△APD的是( ____ )
A.BC=BD B.∠ACB=∠ADB
C.AC=AD D.∠CAB=∠DAB
【解析】解:A、补充BC=BD,先证出△ABC≌△ABD,后能推出△APC≌△APD,故此选项错误;
B、补充∠ACB=∠ADB,先证出△ABC≌△ABD,后能推出△APC≌△APD,故此选项错误.
C、补充AC=AD,不能推出△APC≌△APD,故此选项正确;
D、补充∠CAB=∠DAB,先证出△ABC≌△ABD,后能推出△APC≌△APD,故此选项错误;
故选:C.
C
3.(2023春·浦东新区校级期末)将一副三角板如图所示摆放(其中一块三角板的一条直角边与另一块三角板的斜边摆放在一直线上),那么图中∠α= ____ 度.
【解析】解:∵∠1=45°,∠2=60°,
∴∠α=180°-45°-60°=75°,
故答案为75.
75
4.(2023春·嘉定区期末)如图,已知△ABC≌△ADE,且点B与点D对应,点C与点E对应,点D在BC上,∠BAE=114°,∠BAD=40°,则∠E的度数是 ____ °.
【解析】解:∵△ABC≌△ADE,∴AB=AD,∴∠ABD=∠ADB,
∵∠BAD=40°,∴∠ABD=∠ADB= ???????? (180°-∠BAD)=70°,
∵△ABC≌△ADE,
∴∠ADE=∠ABD=70°,∵∠BAE=114°,∠BAD=40°,
∴∠DAE=∠BAE-∠BAD=114°-40°=74°,
∴∠E=180°-∠ADE-∠DAE=180°-70°-74°=36°,
故答案为:36.
?
36
5.(2023春·虹口区期末)已知等腰三角形的两条边长分别是3cm、7cm,那么这个等腰三角形的周长是 ____ cm.
【解析】解:∵等腰三角形的两条边长分别是3cm、7cm,
∴当此三角形的腰长为3cm时,3+3<7,不能构成三角形,故排除,
∴此三角形的腰长为7cm,底边长为3cm,
∴此等腰三角形的周长=7+7+3=17cm,
故答案为:17.
17
6.(2023春·黄浦区期末)阅读并填空:
如图,△ABC是等腰三角形,AB=AC,D是边AC延长线上的一点,E在边AB上,且连接DE交BC于O,如果OE=OD,那么CD=BE,为什么?
解:过点E作EF∥AC交BC于F,
所以∠ACB=∠EFB(两直线平行,同位角相等),
∠D=∠OEF( ___________________________ ),
在△OCD与△OFE中,
∠????????????=∠????????????(??)????????=????????(已知)∠????=∠????????????(已知) ,
?
两直线平行,内错角相等
所以△OCD≌OFE,( _____ ),
所以CD=FE( ____________________________ ),
因为AB=AC(已知),
所以∠ACB=∠B( _____________ ),
所以∠EFB=∠B(等量代换),
所以BE=FE,
所以CD=BE.
【解析】解:过点E作EF∥AC交BC于F,
所以∠ACB=∠EFB(两直线平行,同位角相等),
∠D=∠OEF(两直线平行,内错角相等),
ASA
全等三角形的对应边相等
等边对等角
在△OCD与△OFE中, ∠????????????=∠????????????(对顶角相等)????????=????????(已知)∠????=∠????????????(已知) ,
所以△OCD≌OFE(ASA),
所以CD=FE(全等三角形的对应边相等),
因为AB=AC(已知),
所以∠ACB=∠B(等边对等角),
所以∠EFB=∠B(等量代换),
所以BE=FE,
所以CD=BE.
故答案为:两直线平行,内错角相等;对顶角相等;ASA;全等三角形的对应边相等;等边对等角.
?
7.(2023春·杨浦区期末 )已知在△ABC中,AB=AC,点D是边AB上一点,∠BCD=∠A.
(1)如图1,试说明CD=CB的理由;
(2)如图2,过点B作BE⊥AC,垂足为点E,BE与CD相交于点F.
①试说明∠BCD=2∠CBE的理由;
②如果△BDF是等腰三角形,求∠A的度数.
________
【解析】解:(1)∵AB=AC,∴∠ABC=∠ACB,
∵∠BDC是△ADC的一个外角,
∴∠BDC=∠A+∠ACD,
∵∠ACB=∠BCD+∠ACD,∠BCD=∠A,
∴∠BDC=∠ACB,
∴∠ABC=∠BDC.
∴CD=CB;
(2)①∵BE⊥AC,
∴∠BEC=90°,
∴∠CBE+∠ACB=90°,
设∠CBE=α,则∠ACB=90°-α,
∴∠ACB=∠ABC=∠BDC=90°-α,
∴∠BCD=180°-∠BDC-∠ABC=180°-(90°-α)-(90°-α)=2α,
∴∠BCD=2∠CBE;
7.(2023春·杨浦区期末 )已知在△ABC中,AB=AC,点D是边AB上一点,∠BCD=∠A.
(1)如图1,试说明CD=CB的理由;
(2)如图2,过点B作BE⊥AC,垂足为点E,BE与CD相交于点F.
①试说明∠BCD=2∠CBE的理由;
②如果△BDF是等腰三角形,求∠A的度数.
________
②∵∠BFD是△CBF的一个外角,
∴∠BFD=∠CBE+∠BCD=α+2α=3α,
分三种情况:当BD=BF时,∴∠BDC=∠BFD=3α,
∵∠ACB=∠ABC=∠BDC=90°-α,∴90°-α=3α,
∴α=22.5°,∴∠A=∠BCD=2α=45°;
当DB=DF时,∴∠DBE=∠BFD=3α,
∵∠DBE=∠ABC-∠CBE=90°-α-α=90°-2α,
∴90°-2α=3α,∴α=18°,∴∠A=∠BCD=2α=36°;
当FB=FD时,∴∠DBE=∠BDF,
∵∠BDF=∠ABC>∠DBF,∴不存在FB=FD,综上所述:如果△BDF是等腰三角形,∠A的度数为45°或36°.
串讲03 三角形
01
02
04
03
目
录
易错易混
题型剖析
考点透视
押题预测
易错易混分析
7道期末真题对应考点练
四大重难点题型典例剖析+强化训练+两类期末重难点突破
四大常考点:知识梳理+考点分类训练
考点透视
C
D
C
不稳定性
6
B
C
99°或29°
20
C
A
B
B
期末重难点突破一:运用数学模型求相关夹角问题
期末重难点突破二:巧作辅助线构造全等三角形
1.(2023春·黄浦区期末 )现有2cm,3cm,5cm,6cm长的四根木棒,任选其中的三根组成三角形,那么可以组成三角形的个数有( ____ )
A.1个 B.2个 C.3个 D.4个
【解析】解:四条木棒的所有组合:2,3,5和2,3,6和2,5,6和3,5,6;
只有2,5,6和3,5,6能组成三角形.
故选:B.
B
押题预测
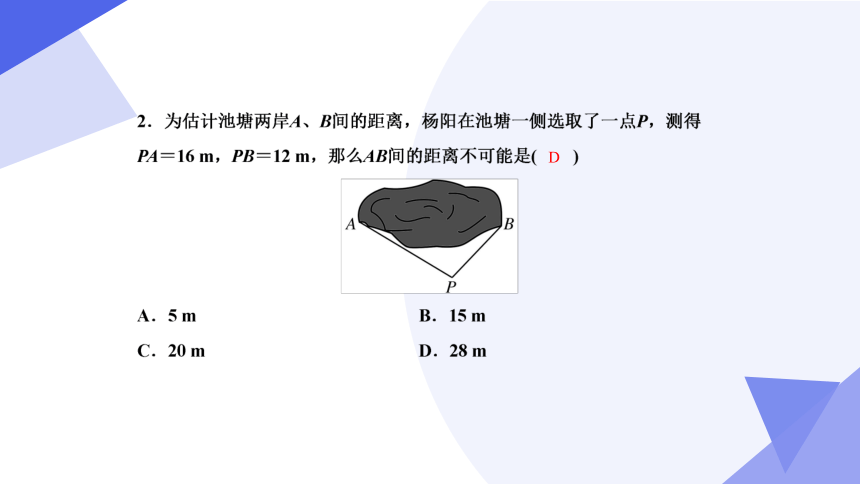
2.(2023春·黄浦区期末)如图,点P是AB上任一点,∠ABC=∠ABD,从下列各条件中补充一个条件,不一定能推出△APC≌△APD的是( ____ )
A.BC=BD B.∠ACB=∠ADB
C.AC=AD D.∠CAB=∠DAB
【解析】解:A、补充BC=BD,先证出△ABC≌△ABD,后能推出△APC≌△APD,故此选项错误;
B、补充∠ACB=∠ADB,先证出△ABC≌△ABD,后能推出△APC≌△APD,故此选项错误.
C、补充AC=AD,不能推出△APC≌△APD,故此选项正确;
D、补充∠CAB=∠DAB,先证出△ABC≌△ABD,后能推出△APC≌△APD,故此选项错误;
故选:C.
C
3.(2023春·浦东新区校级期末)将一副三角板如图所示摆放(其中一块三角板的一条直角边与另一块三角板的斜边摆放在一直线上),那么图中∠α= ____ 度.
【解析】解:∵∠1=45°,∠2=60°,
∴∠α=180°-45°-60°=75°,
故答案为75.
75
4.(2023春·嘉定区期末)如图,已知△ABC≌△ADE,且点B与点D对应,点C与点E对应,点D在BC上,∠BAE=114°,∠BAD=40°,则∠E的度数是 ____ °.
【解析】解:∵△ABC≌△ADE,∴AB=AD,∴∠ABD=∠ADB,
∵∠BAD=40°,∴∠ABD=∠ADB= ???????? (180°-∠BAD)=70°,
∵△ABC≌△ADE,
∴∠ADE=∠ABD=70°,∵∠BAE=114°,∠BAD=40°,
∴∠DAE=∠BAE-∠BAD=114°-40°=74°,
∴∠E=180°-∠ADE-∠DAE=180°-70°-74°=36°,
故答案为:36.
?
36
5.(2023春·虹口区期末)已知等腰三角形的两条边长分别是3cm、7cm,那么这个等腰三角形的周长是 ____ cm.
【解析】解:∵等腰三角形的两条边长分别是3cm、7cm,
∴当此三角形的腰长为3cm时,3+3<7,不能构成三角形,故排除,
∴此三角形的腰长为7cm,底边长为3cm,
∴此等腰三角形的周长=7+7+3=17cm,
故答案为:17.
17
6.(2023春·黄浦区期末)阅读并填空:
如图,△ABC是等腰三角形,AB=AC,D是边AC延长线上的一点,E在边AB上,且连接DE交BC于O,如果OE=OD,那么CD=BE,为什么?
解:过点E作EF∥AC交BC于F,
所以∠ACB=∠EFB(两直线平行,同位角相等),
∠D=∠OEF( ___________________________ ),
在△OCD与△OFE中,
∠????????????=∠????????????(??)????????=????????(已知)∠????=∠????????????(已知) ,
?
两直线平行,内错角相等
所以△OCD≌OFE,( _____ ),
所以CD=FE( ____________________________ ),
因为AB=AC(已知),
所以∠ACB=∠B( _____________ ),
所以∠EFB=∠B(等量代换),
所以BE=FE,
所以CD=BE.
【解析】解:过点E作EF∥AC交BC于F,
所以∠ACB=∠EFB(两直线平行,同位角相等),
∠D=∠OEF(两直线平行,内错角相等),
ASA
全等三角形的对应边相等
等边对等角
在△OCD与△OFE中, ∠????????????=∠????????????(对顶角相等)????????=????????(已知)∠????=∠????????????(已知) ,
所以△OCD≌OFE(ASA),
所以CD=FE(全等三角形的对应边相等),
因为AB=AC(已知),
所以∠ACB=∠B(等边对等角),
所以∠EFB=∠B(等量代换),
所以BE=FE,
所以CD=BE.
故答案为:两直线平行,内错角相等;对顶角相等;ASA;全等三角形的对应边相等;等边对等角.
?
7.(2023春·杨浦区期末 )已知在△ABC中,AB=AC,点D是边AB上一点,∠BCD=∠A.
(1)如图1,试说明CD=CB的理由;
(2)如图2,过点B作BE⊥AC,垂足为点E,BE与CD相交于点F.
①试说明∠BCD=2∠CBE的理由;
②如果△BDF是等腰三角形,求∠A的度数.
________
【解析】解:(1)∵AB=AC,∴∠ABC=∠ACB,
∵∠BDC是△ADC的一个外角,
∴∠BDC=∠A+∠ACD,
∵∠ACB=∠BCD+∠ACD,∠BCD=∠A,
∴∠BDC=∠ACB,
∴∠ABC=∠BDC.
∴CD=CB;
(2)①∵BE⊥AC,
∴∠BEC=90°,
∴∠CBE+∠ACB=90°,
设∠CBE=α,则∠ACB=90°-α,
∴∠ACB=∠ABC=∠BDC=90°-α,
∴∠BCD=180°-∠BDC-∠ABC=180°-(90°-α)-(90°-α)=2α,
∴∠BCD=2∠CBE;
7.(2023春·杨浦区期末 )已知在△ABC中,AB=AC,点D是边AB上一点,∠BCD=∠A.
(1)如图1,试说明CD=CB的理由;
(2)如图2,过点B作BE⊥AC,垂足为点E,BE与CD相交于点F.
①试说明∠BCD=2∠CBE的理由;
②如果△BDF是等腰三角形,求∠A的度数.
________
②∵∠BFD是△CBF的一个外角,
∴∠BFD=∠CBE+∠BCD=α+2α=3α,
分三种情况:当BD=BF时,∴∠BDC=∠BFD=3α,
∵∠ACB=∠ABC=∠BDC=90°-α,∴90°-α=3α,
∴α=22.5°,∴∠A=∠BCD=2α=45°;
当DB=DF时,∴∠DBE=∠BFD=3α,
∵∠DBE=∠ABC-∠CBE=90°-α-α=90°-2α,
∴90°-2α=3α,∴α=18°,∴∠A=∠BCD=2α=36°;
当FB=FD时,∴∠DBE=∠BDF,
∵∠BDF=∠ABC>∠DBF,∴不存在FB=FD,综上所述:如果△BDF是等腰三角形,∠A的度数为45°或36°.
同课章节目录
