专题03四边形(考点串讲)-八年级数学下学期期末考点大串讲(沪教版)
文档属性
| 名称 | 专题03四边形(考点串讲)-八年级数学下学期期末考点大串讲(沪教版) |
|
|
| 格式 | pptx | ||
| 文件大小 | 3.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-31 00:00:00 | ||
图片预览








文档简介
(共56张PPT)
八年级沪教版数学下册期末考点大串讲
串讲03 四边形
01
02
04
03
目
录
易错易混
题型剖析
考点透视
押题预测
四大易错易混经典例题
5道期末真题对应考点练
五大重难点题型典例剖析+三种技巧总结
四大常考点:知识梳理
考点一 多边形
多边形的性质 内角和 n 边形内角和为 .
外角和 任意多边形的外角和为 。
(n-2)·180°
360°
考点透视
正多 边形 定义 各个角________,各条边________的多边形叫正多边形
对称性 正多边形都是________对称图形,边数为偶数的正多边形是中心对称图形
相等
相等
轴
定义:
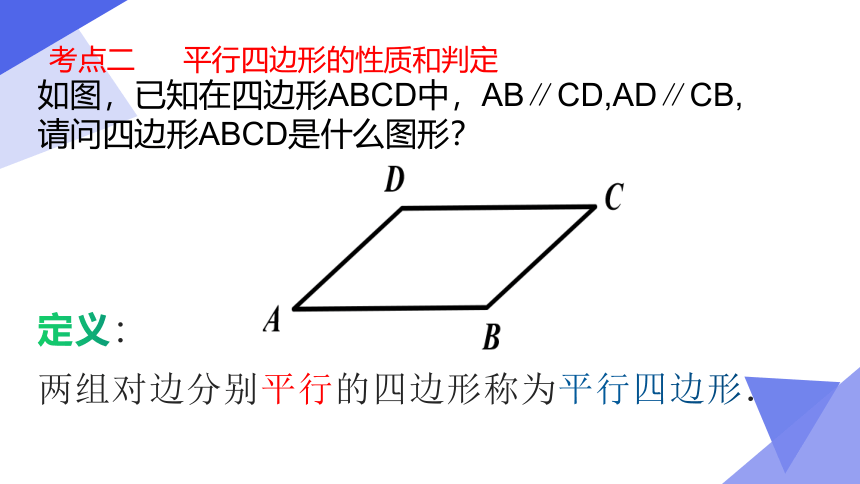
两组对边分别平行的四边形称为平行四边形.
如图,已知在四边形ABCD中,AB∥CD,AD∥CB,请问四边形ABCD是什么图形?
考点二 平行四边形的性质和判定
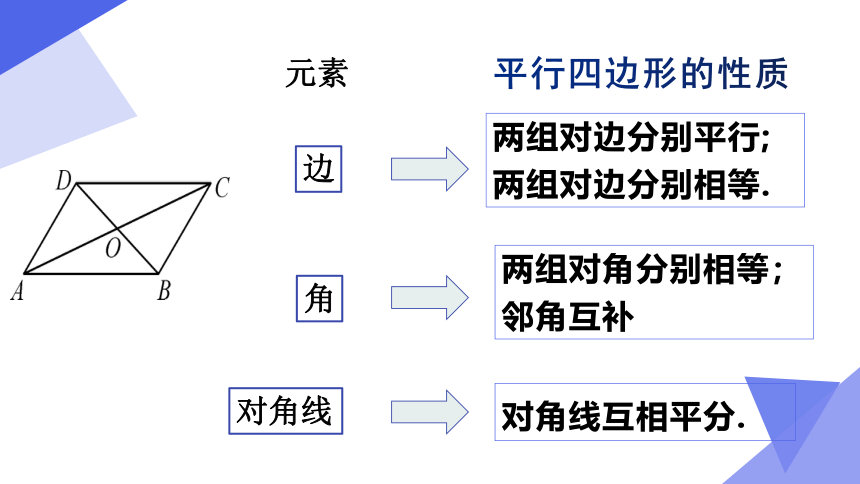
平行四边形的性质
元素
对角线
角
边
两组对边分别平行;
两组对边分别相等.
两组对角分别相等;
邻角互补
对角线互相平分.
平行四边形的对称性:
对称性:平行四边形是中心对称图形;
对称中心:对角线的交点。
平行四边形的判定:
四边形
平行四边形
边
两组对边分别相等。
两组对边分别平行。
一组对边平行且相等。
角
对角线
两组对角分别相等。
两条对角线互相平分。
1、梯形:是指一组对边 而另一组对边
的四边形;
或指一组对边 且 的四边形。
2、特殊的梯形有: 、 。
3、梯形的中位线:连接梯形两腰的 的 线段。梯形中位线的长度等于 。
平行
不平行
平行
不相等
等腰梯形
直角梯形
中点
两底和的一半
考点三 梯形
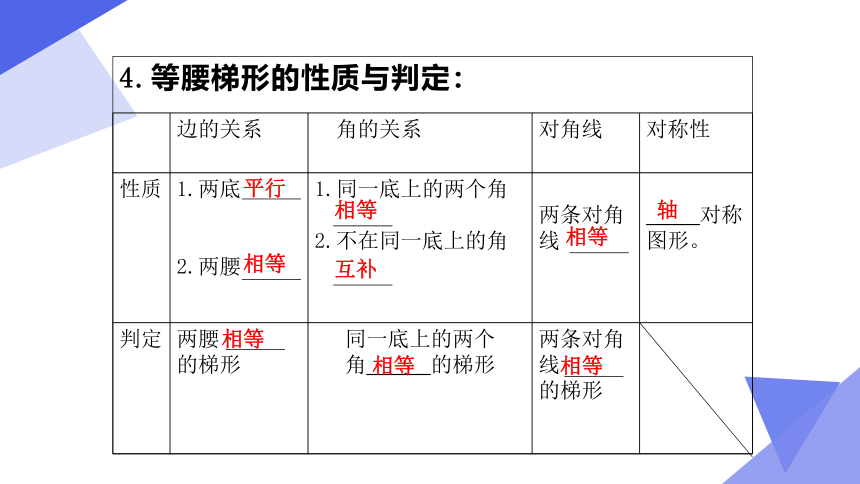
4.等腰梯形的性质与判定:
边的关系 角的关系 对角线 对称性
性质 两底 2.两腰 同一底上的两个角 2.不在同一底上的角 两条对角线
对称图形。
判定 两腰 的梯形 同一底上的两个 角 的梯形 两条对角线 的梯形
相等
平行
相等
互补
相等
轴
相等
相等
相等
5.三角形 中位线的性质
定理:三角形的中位线平行于第三边,
且等于第三边的一半.
这个定理提供了证明线段平行以及线段成倍分关系的根据.
∵D、E是AB、AC的中点,
D
E
B
C
A
∴DE∥BC,
F
向量:既有大小、又有方向的量.
几何表示:
有向线段
A
B
符号语言: ,
模: ,
位置向量
自由向量
相等向量
相反向量
平行向量
向量的模型——位移
从始点A出发到终点B的过程中的位移为 .
位移由运动过程中的始点和终点确定,而与运动的路径无关.
考点四:平面向量
一、向量加法的运算(作图)法则:
二、向量减法的运算(作图)法则:
1、三角形法则,(起点和终点重合)
2、多边形形法则(首尾依次相连接)
1、三角形法则(共起点,尾相连)
3、平行四边形法则(共起点,做平行四边形)
2、平行四边形法则(共起点,做平行四边形)
以共起点为起点的对角线向量,就是a,b的和向量;
与被减向量共终点的对角线向量,就是a,b的差向量。
平面向量的加减
A
C
题型剖析
不唯一,如DE=EC
32cm或34cm
C
AB=BC或AC⊥BD
A
11.如图,在梯形ABCD中,AB∥CD,点E、F分别是AD、BC的中点,如果AB=2,EF=3,那么CD= ____ .
【解析】解:在梯形ABCD中,AB∥CD,点E、F分别是AD、BC的中点,
∴EF是梯形ABCD的中位线,
∴EF= (AB+CD),
∴CD=2EF-AB=6-2=4.
故答案为:4.
4
考点4:梯形
12.如图,梯形ABCD中,AD∥BC,∠BAC=90°,AB=AC,对角线AC与BD相交于点O,且BD=BC,那么∠AOB= ____ 度.
【解析】解:如图,作AF⊥BC于F,DE⊥BC于E,
在Rt△ABC中,
∵AB=AC,∠BAC=90°,∴∠ABC=∠ACB=45°,
∴BC= AB,AF= AB,∴AF= BC.
又∵DE=AF,∴DE= BC= BD,∴ = ,
∴∠1=30°,∴∠BOC=180°-30°-45°=105°,
∴∠AOB=180°-∠BOC=180°-105°=75°,
故答案为:75.
75
13.下列等式中不正确的是( ____ )
A.
B.-(- )=
C.( + )+ = +( + )
D. +(- )= -
【解析】解:A、 ,符合题意;
B、-(- )= ,不符合题意;
C、( + )+ = +( + ),不符合题意;
A
D、 +(- )= - ,不符合题意.
故选:A.
考点5:平面向量
14.如图,已知在△ABC中,点D是边AC的中点,设 ,用向量 、 表示向量 = .
【解析】解:∵点D是边AC的中点,
∴ ,
又∵ ,
∴ =- ,
故答案为:- .
技巧1:特殊平行四边形的证明与计算
技巧总结
C
A
B
技巧2:四边形中的图形变换
C
B
5
6
40°
B
技巧3:解决梯形问题的基本思路和方法:
通过添加适当的辅助线,把梯形问题转化为平行四边形和三角形的问题来解决。
常画的辅助线有以下几种:
B
A
D
C
E
作一腰平行线
B
A
D
C
E
F
作高线
E
B
A
D
C
延长两腰
B
C
D
A
O
E
作对角线的平行线
11.在直角梯形ABCD中,AD//BC, ∠ A=90°,
AD=10cm,DC=13cm,BC=15cm,求AB的长。
作高,将梯形问题转化成直角三角形和矩形.
解:作DE⊥BC于点E ,则∠DEB=90°
∵ AD//BC,
∴ ∠A+ ∠ B=180 °
∵ ∠A=90 °
∴ ∠B=90 °
∵ ∠A=90 °,∠B=90 °,∠DEB=90°
∴四边形ABED是矩形
∴AD= BE,AB=DE
∵AD=10cm,BC=15cm
∴EC=BC-BE=BC-AD=5cm
在Rt△DEC中,
∵ ∠DEC=90°
∴
∴AB=12cm
12.如图,在梯形ABCD中,AB//CD,
∠D=2 ∠B,AD=10,AB=15,求CD的长。
平移一腰,将梯形问题转化成三角形和
平行四边形.
解:作CE //DA交AB于点E
∵ AB//DC, CE //DA
∴四边形AECD是平行四边形
∴CE=DA, DC=AE, ∠D= ∠ 1
∵AD=10 ,∠D= 2∠ B
∴CE=10, ∠1= 2∠ B
∵ ∠1= ∠ B+ ∠ 2
∴∠2= ∠ B
∴EB= EC=10
∵AB=15
∴AE=AB-EB=5
∴CD=5
E
1
2
B
易错易混
B
C
(3,2)或(-3,2)或(5,-2)
1.(2023春·黄浦区期末 )已知向量 、 满足| |=| |,则( ____ )
A. = B. =-
C. ∥ D.以上都有可能
【解析】解:若向量 、 满足| |=| |,
可得: = ,或 =- ,或 ∥ ,
故选:D.
D
押题预测
2.(2023春·浦东新区校级期末)一个正多边形的每一个内角都是140°,则这个正多边形的边数是 ____
【解析】解:180°-140°=40°,
360°÷40°=9.
故答案为:九.
九
3.(2023春·杨浦区期末)已知菱形的周长为40,一条对角线长为12,则这个菱形的面积是 ____ .
【解析】解:因为周长是40,所以边长是10.
如图所示:AB=10,AC=12.
根据菱形的性质,AC⊥BD,AO=6,
∴BO=8,BD=16.
∴面积S= AC×BD=12×16× =96.
故答案为96.
96
4.(2023春·浦东新区校级期末)如图,已知矩形ABCD的对角线交于点O,点E、F和G分别平分线段AB、OD和OA.
(1)求证:四边形OFGE是平行四边形.
(2)猜想:当∠ABD= ____ °时四边形OFGE是菱形,并证明.
【解析】(1)证明:∵矩形ABCD的对角线交于点O,∴OD=OB=OA,
又∵点E、F和G分别平分线段AB、OD和OA,
∴OE为△ABD的中位线,FG为△AOD的中位线,
∴ ,OE∥AD,FG∥AD, ,∴OE∥FG,OE=FG,
∴四边形OFGE是平行四边形;
(2)解:由(1)知,四边形OFGE是平行四边形,当四边形OFGE是菱形时,
则OF=FG,∴OD=AD,∴△AOD为等边三角形,
∴∠ADB=60°,∴∠ABD=30°,
∴当∠ABD=30°时,四边形OFGE是菱形.
故答案为:30.
30
5.(2023春·黄浦区期末)已知:如图,在平行四边形ABCD中,点E、F分别是AD、BC的中点,点G、H分别在边AB、CD上,且AG=CH.
(1)求证:△AGE≌△CHF;
(2)若∠AEG+∠BFG=90°,求证:四边形EGFH是矩形.
【解析】(1)证明:∵四边形ABCD是平行四边形,
∴∠A=∠C,AD=BC,AB=CD,
∵点E、F分别是AD、BC的中点,
∴AE= AD,CF= BC,∴AE=DE=BF=CF,
在△AGE与△CHF中,
,
∴△AGE≌△CHF(SAS);
(2)证明:∵四边形ABCD是平行四边形,
∴∠B=∠D,AD=BC,AB=CD,
∵点E、F分别是AD、BC的中点,
∴DE= AD,BF= BC,∴DE=BF,
∵AG=CH,∴AB-AG=CD-CH,即BG=DH,
∴△BFG≌△DEH(SAS);∴FG=EH,
由(1)知△AGE≌△CHF,∴EG=FH,∠AEG=∠CFH,
∴四边形EGFH是平行四边形,
∵∠AEG+∠BFG=90°,∴∠CFH+∠BFG=90°,
∴∠GFH=90°,∴四边形EGFH是矩形.
5.(2023春·黄浦区期末)已知:如图,在平行四边形ABCD中,点E、F分别是AD、BC的中点,点G、H分别在边AB、CD上,且AG=CH.
(1)求证:△AGE≌△CHF;
(2)若∠AEG+∠BFG=90°,求证:四边形EGFH是矩形.
八年级沪教版数学下册期末考点大串讲
串讲03 四边形
01
02
04
03
目
录
易错易混
题型剖析
考点透视
押题预测
四大易错易混经典例题
5道期末真题对应考点练
五大重难点题型典例剖析+三种技巧总结
四大常考点:知识梳理
考点一 多边形
多边形的性质 内角和 n 边形内角和为 .
外角和 任意多边形的外角和为 。
(n-2)·180°
360°
考点透视
正多 边形 定义 各个角________,各条边________的多边形叫正多边形
对称性 正多边形都是________对称图形,边数为偶数的正多边形是中心对称图形
相等
相等
轴
定义:
两组对边分别平行的四边形称为平行四边形.
如图,已知在四边形ABCD中,AB∥CD,AD∥CB,请问四边形ABCD是什么图形?
考点二 平行四边形的性质和判定
平行四边形的性质
元素
对角线
角
边
两组对边分别平行;
两组对边分别相等.
两组对角分别相等;
邻角互补
对角线互相平分.
平行四边形的对称性:
对称性:平行四边形是中心对称图形;
对称中心:对角线的交点。
平行四边形的判定:
四边形
平行四边形
边
两组对边分别相等。
两组对边分别平行。
一组对边平行且相等。
角
对角线
两组对角分别相等。
两条对角线互相平分。
1、梯形:是指一组对边 而另一组对边
的四边形;
或指一组对边 且 的四边形。
2、特殊的梯形有: 、 。
3、梯形的中位线:连接梯形两腰的 的 线段。梯形中位线的长度等于 。
平行
不平行
平行
不相等
等腰梯形
直角梯形
中点
两底和的一半
考点三 梯形
4.等腰梯形的性质与判定:
边的关系 角的关系 对角线 对称性
性质 两底 2.两腰 同一底上的两个角 2.不在同一底上的角 两条对角线
对称图形。
判定 两腰 的梯形 同一底上的两个 角 的梯形 两条对角线 的梯形
相等
平行
相等
互补
相等
轴
相等
相等
相等
5.三角形 中位线的性质
定理:三角形的中位线平行于第三边,
且等于第三边的一半.
这个定理提供了证明线段平行以及线段成倍分关系的根据.
∵D、E是AB、AC的中点,
D
E
B
C
A
∴DE∥BC,
F
向量:既有大小、又有方向的量.
几何表示:
有向线段
A
B
符号语言: ,
模: ,
位置向量
自由向量
相等向量
相反向量
平行向量
向量的模型——位移
从始点A出发到终点B的过程中的位移为 .
位移由运动过程中的始点和终点确定,而与运动的路径无关.
考点四:平面向量
一、向量加法的运算(作图)法则:
二、向量减法的运算(作图)法则:
1、三角形法则,(起点和终点重合)
2、多边形形法则(首尾依次相连接)
1、三角形法则(共起点,尾相连)
3、平行四边形法则(共起点,做平行四边形)
2、平行四边形法则(共起点,做平行四边形)
以共起点为起点的对角线向量,就是a,b的和向量;
与被减向量共终点的对角线向量,就是a,b的差向量。
平面向量的加减
A
C
题型剖析
不唯一,如DE=EC
32cm或34cm
C
AB=BC或AC⊥BD
A
11.如图,在梯形ABCD中,AB∥CD,点E、F分别是AD、BC的中点,如果AB=2,EF=3,那么CD= ____ .
【解析】解:在梯形ABCD中,AB∥CD,点E、F分别是AD、BC的中点,
∴EF是梯形ABCD的中位线,
∴EF= (AB+CD),
∴CD=2EF-AB=6-2=4.
故答案为:4.
4
考点4:梯形
12.如图,梯形ABCD中,AD∥BC,∠BAC=90°,AB=AC,对角线AC与BD相交于点O,且BD=BC,那么∠AOB= ____ 度.
【解析】解:如图,作AF⊥BC于F,DE⊥BC于E,
在Rt△ABC中,
∵AB=AC,∠BAC=90°,∴∠ABC=∠ACB=45°,
∴BC= AB,AF= AB,∴AF= BC.
又∵DE=AF,∴DE= BC= BD,∴ = ,
∴∠1=30°,∴∠BOC=180°-30°-45°=105°,
∴∠AOB=180°-∠BOC=180°-105°=75°,
故答案为:75.
75
13.下列等式中不正确的是( ____ )
A.
B.-(- )=
C.( + )+ = +( + )
D. +(- )= -
【解析】解:A、 ,符合题意;
B、-(- )= ,不符合题意;
C、( + )+ = +( + ),不符合题意;
A
D、 +(- )= - ,不符合题意.
故选:A.
考点5:平面向量
14.如图,已知在△ABC中,点D是边AC的中点,设 ,用向量 、 表示向量 = .
【解析】解:∵点D是边AC的中点,
∴ ,
又∵ ,
∴ =- ,
故答案为:- .
技巧1:特殊平行四边形的证明与计算
技巧总结
C
A
B
技巧2:四边形中的图形变换
C
B
5
6
40°
B
技巧3:解决梯形问题的基本思路和方法:
通过添加适当的辅助线,把梯形问题转化为平行四边形和三角形的问题来解决。
常画的辅助线有以下几种:
B
A
D
C
E
作一腰平行线
B
A
D
C
E
F
作高线
E
B
A
D
C
延长两腰
B
C
D
A
O
E
作对角线的平行线
11.在直角梯形ABCD中,AD//BC, ∠ A=90°,
AD=10cm,DC=13cm,BC=15cm,求AB的长。
作高,将梯形问题转化成直角三角形和矩形.
解:作DE⊥BC于点E ,则∠DEB=90°
∵ AD//BC,
∴ ∠A+ ∠ B=180 °
∵ ∠A=90 °
∴ ∠B=90 °
∵ ∠A=90 °,∠B=90 °,∠DEB=90°
∴四边形ABED是矩形
∴AD= BE,AB=DE
∵AD=10cm,BC=15cm
∴EC=BC-BE=BC-AD=5cm
在Rt△DEC中,
∵ ∠DEC=90°
∴
∴AB=12cm
12.如图,在梯形ABCD中,AB//CD,
∠D=2 ∠B,AD=10,AB=15,求CD的长。
平移一腰,将梯形问题转化成三角形和
平行四边形.
解:作CE //DA交AB于点E
∵ AB//DC, CE //DA
∴四边形AECD是平行四边形
∴CE=DA, DC=AE, ∠D= ∠ 1
∵AD=10 ,∠D= 2∠ B
∴CE=10, ∠1= 2∠ B
∵ ∠1= ∠ B+ ∠ 2
∴∠2= ∠ B
∴EB= EC=10
∵AB=15
∴AE=AB-EB=5
∴CD=5
E
1
2
B
易错易混
B
C
(3,2)或(-3,2)或(5,-2)
1.(2023春·黄浦区期末 )已知向量 、 满足| |=| |,则( ____ )
A. = B. =-
C. ∥ D.以上都有可能
【解析】解:若向量 、 满足| |=| |,
可得: = ,或 =- ,或 ∥ ,
故选:D.
D
押题预测
2.(2023春·浦东新区校级期末)一个正多边形的每一个内角都是140°,则这个正多边形的边数是 ____
【解析】解:180°-140°=40°,
360°÷40°=9.
故答案为:九.
九
3.(2023春·杨浦区期末)已知菱形的周长为40,一条对角线长为12,则这个菱形的面积是 ____ .
【解析】解:因为周长是40,所以边长是10.
如图所示:AB=10,AC=12.
根据菱形的性质,AC⊥BD,AO=6,
∴BO=8,BD=16.
∴面积S= AC×BD=12×16× =96.
故答案为96.
96
4.(2023春·浦东新区校级期末)如图,已知矩形ABCD的对角线交于点O,点E、F和G分别平分线段AB、OD和OA.
(1)求证:四边形OFGE是平行四边形.
(2)猜想:当∠ABD= ____ °时四边形OFGE是菱形,并证明.
【解析】(1)证明:∵矩形ABCD的对角线交于点O,∴OD=OB=OA,
又∵点E、F和G分别平分线段AB、OD和OA,
∴OE为△ABD的中位线,FG为△AOD的中位线,
∴ ,OE∥AD,FG∥AD, ,∴OE∥FG,OE=FG,
∴四边形OFGE是平行四边形;
(2)解:由(1)知,四边形OFGE是平行四边形,当四边形OFGE是菱形时,
则OF=FG,∴OD=AD,∴△AOD为等边三角形,
∴∠ADB=60°,∴∠ABD=30°,
∴当∠ABD=30°时,四边形OFGE是菱形.
故答案为:30.
30
5.(2023春·黄浦区期末)已知:如图,在平行四边形ABCD中,点E、F分别是AD、BC的中点,点G、H分别在边AB、CD上,且AG=CH.
(1)求证:△AGE≌△CHF;
(2)若∠AEG+∠BFG=90°,求证:四边形EGFH是矩形.
【解析】(1)证明:∵四边形ABCD是平行四边形,
∴∠A=∠C,AD=BC,AB=CD,
∵点E、F分别是AD、BC的中点,
∴AE= AD,CF= BC,∴AE=DE=BF=CF,
在△AGE与△CHF中,
,
∴△AGE≌△CHF(SAS);
(2)证明:∵四边形ABCD是平行四边形,
∴∠B=∠D,AD=BC,AB=CD,
∵点E、F分别是AD、BC的中点,
∴DE= AD,BF= BC,∴DE=BF,
∵AG=CH,∴AB-AG=CD-CH,即BG=DH,
∴△BFG≌△DEH(SAS);∴FG=EH,
由(1)知△AGE≌△CHF,∴EG=FH,∠AEG=∠CFH,
∴四边形EGFH是平行四边形,
∵∠AEG+∠BFG=90°,∴∠CFH+∠BFG=90°,
∴∠GFH=90°,∴四边形EGFH是矩形.
5.(2023春·黄浦区期末)已知:如图,在平行四边形ABCD中,点E、F分别是AD、BC的中点,点G、H分别在边AB、CD上,且AG=CH.
(1)求证:△AGE≌△CHF;
(2)若∠AEG+∠BFG=90°,求证:四边形EGFH是矩形.
同课章节目录
