三阶行列式 课件
图片预览






文档简介
(共17张PPT)
第九章 矩阵和行列式初步
9.4.2 三阶行列式
9.4.3 三阶行列式
一、三阶行列式的展开II(续)
定理1:三阶行列式等于其任意列(或行)的所有元
素分别和它们的代数余子式的乘积的和.
一、三阶行列式的展开II(续)
定理1:三阶行列式等于其任意列(或行)的所有元
素分别和它们的代数余子式的乘积的和.
证:
例1.将行列式 按第1列和第2行分别
展开并求值.
解:
一般选择0较多的行或列进行展开求值.
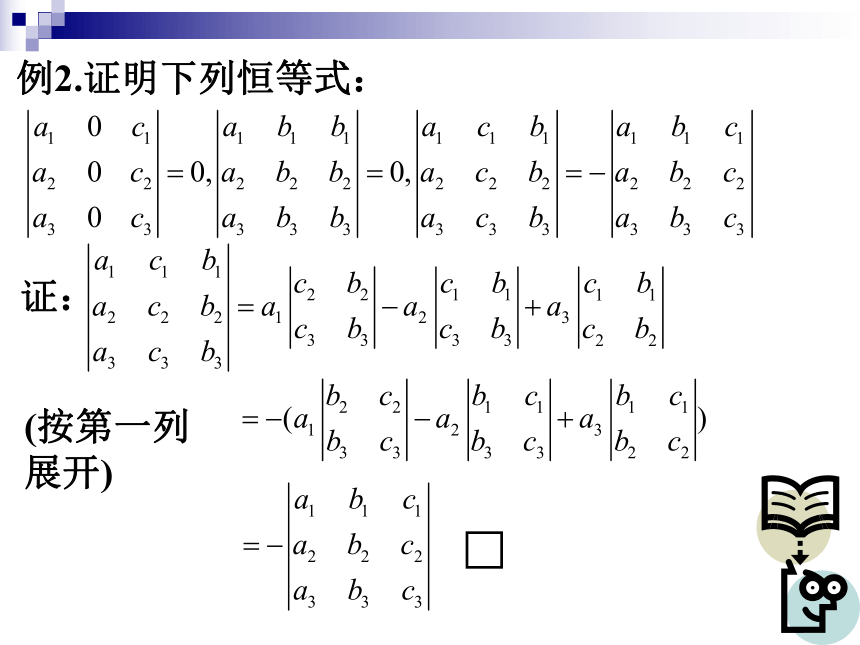
例2.证明下列恒等式:
证:
(按第二列展开)
(按第一列展开)
例2.证明下列恒等式:
证:
(按第一列 展开)
一、三阶行列式的展开II(续)
定理2:三阶行列式某一列(或行)的各元素分别与
另一列(或行)的对应元素的代数余子式的乘积的和
等于零.
………
证:
例3. 行列式 中,元素 的代
数余子式分别是 ,计算:
解:根据定理1、2可知
原式=
(选用)例4.如图,在平面直角坐标系中,点
的坐标分别是
求
面积公式.
的坐标分别是
求
面积公式.
(选用)例4.如图,在平面直角坐标系中,点
的坐标分别是
求
面积公式.
(选用)例4.如图,在平面直角坐标系中,点
①
③
假设存在
使得:
②
若
则:
课外阅读材料——行列式按第一列展开的合理性
改写为:
解出:
不妨令:
且
所以定义:
第九章 矩阵和行列式初步
9.4.2 三阶行列式
9.4.3 三阶行列式
一、三阶行列式的展开II(续)
定理1:三阶行列式等于其任意列(或行)的所有元
素分别和它们的代数余子式的乘积的和.
一、三阶行列式的展开II(续)
定理1:三阶行列式等于其任意列(或行)的所有元
素分别和它们的代数余子式的乘积的和.
证:
例1.将行列式 按第1列和第2行分别
展开并求值.
解:
一般选择0较多的行或列进行展开求值.
例2.证明下列恒等式:
证:
(按第二列展开)
(按第一列展开)
例2.证明下列恒等式:
证:
(按第一列 展开)
一、三阶行列式的展开II(续)
定理2:三阶行列式某一列(或行)的各元素分别与
另一列(或行)的对应元素的代数余子式的乘积的和
等于零.
………
证:
例3. 行列式 中,元素 的代
数余子式分别是 ,计算:
解:根据定理1、2可知
原式=
(选用)例4.如图,在平面直角坐标系中,点
的坐标分别是
求
面积公式.
的坐标分别是
求
面积公式.
(选用)例4.如图,在平面直角坐标系中,点
的坐标分别是
求
面积公式.
(选用)例4.如图,在平面直角坐标系中,点
①
③
假设存在
使得:
②
若
则:
课外阅读材料——行列式按第一列展开的合理性
改写为:
解出:
不妨令:
且
所以定义:
