24.1.3弧、弦、圆心角(27张PPT)
文档属性
| 名称 | 24.1.3弧、弦、圆心角(27张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 366.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-12-04 14:03:43 | ||
图片预览





文档简介
课件27张PPT。24.1.3 弧、弦、圆心角学科网学.科.网圆是中心对称图形吗?它的对称中心在哪里?·一、思考圆是中心对称图形,它的对称中心是圆心.圆有旋转不变性圆的性质圆是轴对称图形,每一条直径所在的直线都是对称轴。
圆是以圆心为对称中心的中心对称图形。
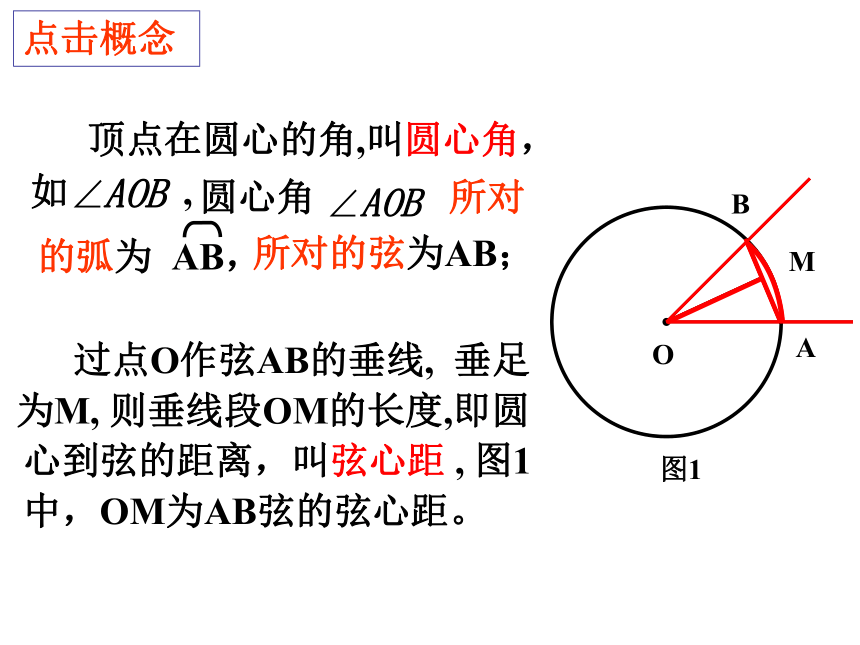
圆还具有旋转不变性,即圆绕圆心旋转任意一个角度α,都能与原来的图形重合。 过点O作弦AB的垂线, 垂足
为M,AB 顶点在圆心的角,叫圆心角,
如 , 所对的弦为AB;图1 则垂线段OM的长度,即圆
心到弦的距离,叫弦心距 , 图1
中,OM为AB弦的弦心距。点击概念1、判别下列各图中的角是不是圆心角,
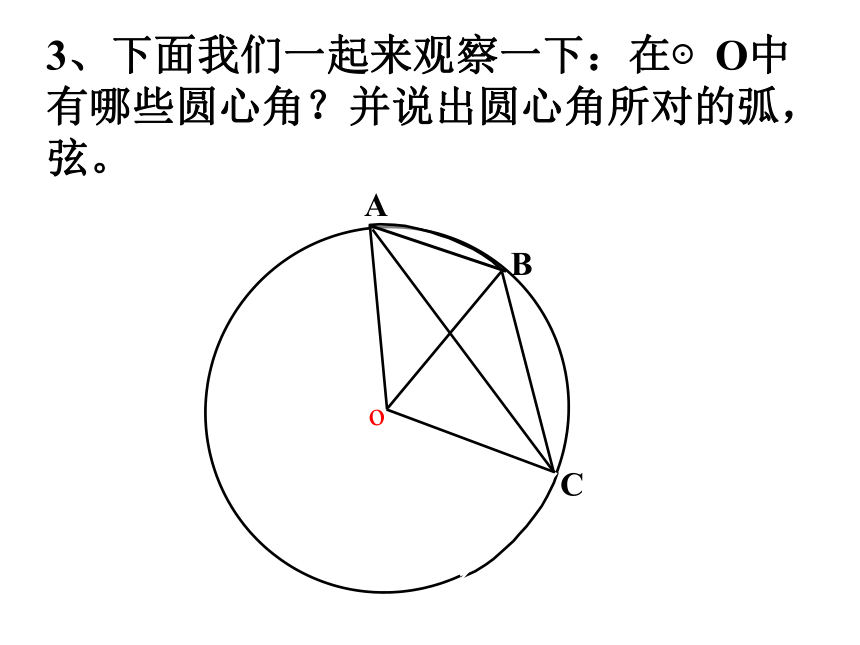
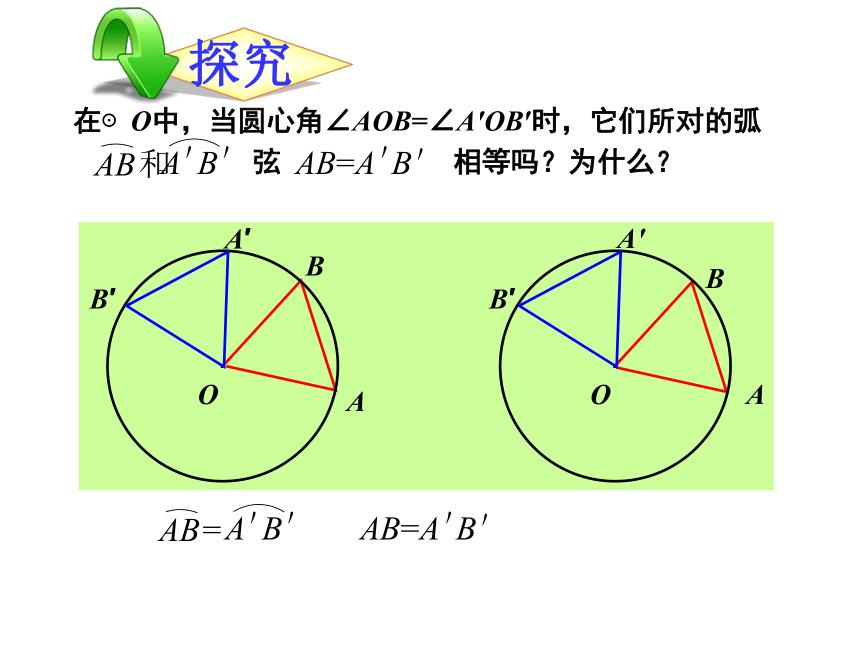
并说明理由。①②③④学科网2、下列图中弦心距做对了的是( )┐┐①②③④3、下面我们一起来观察一下:在⊙O中有哪些圆心角?并说出圆心角所对的弧,弦。 在⊙O中,当圆心角∠AOB=∠A′OB′时,它们所对的弧
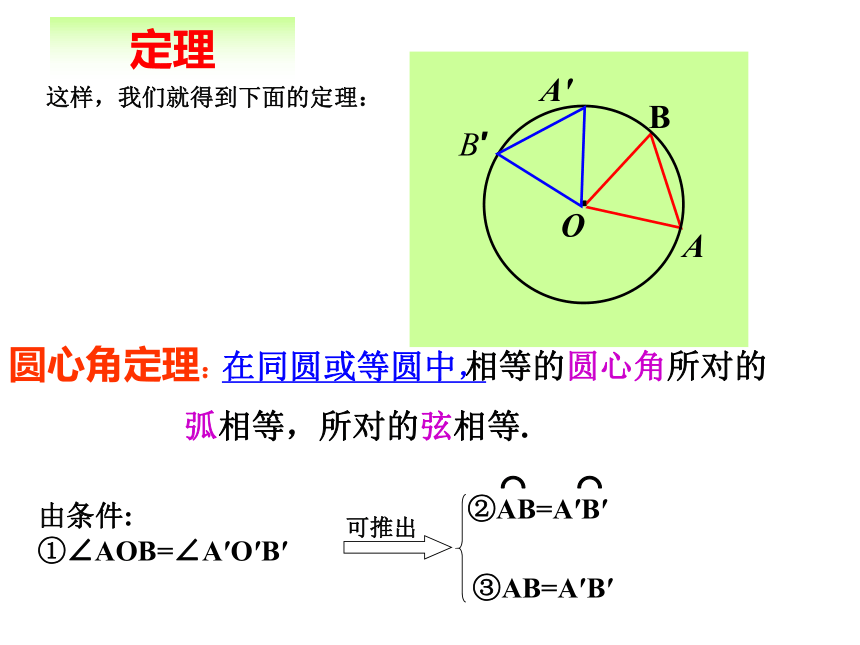
弦 相等吗?为什么?·OAB·OABA′B′A′B′这样,我们就得到下面的定理:定理圆心角定理: 相等的圆心角所对的
弧相等,所对的弦相等. 在同圆或等圆中,由条件:
①∠AOB=∠A′O′B′③AB=A′B′zxxkw如图: ∠AOB=∠COD,
那么 吗?思考:条件是:在同圆或等圆中.①∠AOB=∠A′O′B′③AB=A′B′弧、弦、圆心角关系定理的推论 在同圆或等圆中,相等的弧所对的圆心角相等,所对的弦相等.弧、弦、圆心角关系定理的推论①∠AOB=∠A′O′B′③AB=A′B′ 在同圆或等圆中,相等的弦所对的圆心角相等,所对的弧相等,所对的弦的弦心距相等.弧、弦与圆心角的关系定理小结在同圆或等圆中,两个圆心角、两条弧、两条弦中有一组量相等,它们所对应的其余各组量也相等.延伸 圆心角定理及推论整体理解:(1) 圆心角(2) 弧(3) 弦知一得二αAA′B ′αB 如图,AB、CD是⊙O的两条弦.
(1)如果AB=CD,那么___________,_________________.
(2)如果 ,那么____________,_____________.
(3)如果∠AOB=∠COD,那么_____________,_________.
(4)如果AB=CD,OE⊥AB于E,OF⊥CD于F,OE与OF相等吗?为什么?AB=CDAB=CD练习 OE﹦OF判断:
1、等弦所对的弧相等。 ( )
2、等弧所对的弦相等。 ( )
3、圆心角相等,所对的弦相等。( )
4、弦相等,所对的圆心角相等。( )
×××√zxxkw证明:∵∴ AB=AC, △ABC等腰三角形.又∠ACB=60°,∴ △ABC是等边三角形,
AB=BC=CA.∴ ∠AOB=∠BOC=∠AOC.·ABCO例题例1 如图在⊙O中, ,∠ACB=60°,求证∠AOB=∠BOC=∠AOC.1、如图,AB是⊙O 的直径, ∠COD=35°,求∠AOE 的度数.解:练习∵3、已知:如图,A,B,C,D是⊙O上的点,∠1=∠2。求证:AC=BDzxxkw3、如图,已知AD=BC、求证AB=CD. OABCD变式:如图,如果弧AD=弧BC,求证:AB=CD做一做:随堂训练例1 如图,已知点O是∠EPF 的平分线上一点,P点在圆外,
以O为圆心的圆与∠EPF 的两边分别相交于A、B和C、D。
求证:AB=CD分析: 联想到“角平分线的性质”,作弦心距OM、ON, 证明: 作 , 垂足分别为M 、 N 。.PABECDF要证AB=CD ,只需证OM=ONOzxxkw.如图,P点在圆上,PB=PD吗?
P点在圆内,AB=CD吗?思考:PBEDFO3、如图,BC为⊙O的直径,OA是⊙O的半径,弦BE∥OA。
求证:AC=AE⌒ ⌒圆心角定理:在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦相等,所对的弦的弦心距相等.zxxkw
圆是以圆心为对称中心的中心对称图形。
圆还具有旋转不变性,即圆绕圆心旋转任意一个角度α,都能与原来的图形重合。 过点O作弦AB的垂线, 垂足
为M,AB 顶点在圆心的角,叫圆心角,
如 , 所对的弦为AB;图1 则垂线段OM的长度,即圆
心到弦的距离,叫弦心距 , 图1
中,OM为AB弦的弦心距。点击概念1、判别下列各图中的角是不是圆心角,
并说明理由。①②③④学科网2、下列图中弦心距做对了的是( )┐┐①②③④3、下面我们一起来观察一下:在⊙O中有哪些圆心角?并说出圆心角所对的弧,弦。 在⊙O中,当圆心角∠AOB=∠A′OB′时,它们所对的弧
弦 相等吗?为什么?·OAB·OABA′B′A′B′这样,我们就得到下面的定理:定理圆心角定理: 相等的圆心角所对的
弧相等,所对的弦相等. 在同圆或等圆中,由条件:
①∠AOB=∠A′O′B′③AB=A′B′zxxkw如图: ∠AOB=∠COD,
那么 吗?思考:条件是:在同圆或等圆中.①∠AOB=∠A′O′B′③AB=A′B′弧、弦、圆心角关系定理的推论 在同圆或等圆中,相等的弧所对的圆心角相等,所对的弦相等.弧、弦、圆心角关系定理的推论①∠AOB=∠A′O′B′③AB=A′B′ 在同圆或等圆中,相等的弦所对的圆心角相等,所对的弧相等,所对的弦的弦心距相等.弧、弦与圆心角的关系定理小结在同圆或等圆中,两个圆心角、两条弧、两条弦中有一组量相等,它们所对应的其余各组量也相等.延伸 圆心角定理及推论整体理解:(1) 圆心角(2) 弧(3) 弦知一得二αAA′B ′αB 如图,AB、CD是⊙O的两条弦.
(1)如果AB=CD,那么___________,_________________.
(2)如果 ,那么____________,_____________.
(3)如果∠AOB=∠COD,那么_____________,_________.
(4)如果AB=CD,OE⊥AB于E,OF⊥CD于F,OE与OF相等吗?为什么?AB=CDAB=CD练习 OE﹦OF判断:
1、等弦所对的弧相等。 ( )
2、等弧所对的弦相等。 ( )
3、圆心角相等,所对的弦相等。( )
4、弦相等,所对的圆心角相等。( )
×××√zxxkw证明:∵∴ AB=AC, △ABC等腰三角形.又∠ACB=60°,∴ △ABC是等边三角形,
AB=BC=CA.∴ ∠AOB=∠BOC=∠AOC.·ABCO例题例1 如图在⊙O中, ,∠ACB=60°,求证∠AOB=∠BOC=∠AOC.1、如图,AB是⊙O 的直径, ∠COD=35°,求∠AOE 的度数.解:练习∵3、已知:如图,A,B,C,D是⊙O上的点,∠1=∠2。求证:AC=BDzxxkw3、如图,已知AD=BC、求证AB=CD. OABCD变式:如图,如果弧AD=弧BC,求证:AB=CD做一做:随堂训练例1 如图,已知点O是∠EPF 的平分线上一点,P点在圆外,
以O为圆心的圆与∠EPF 的两边分别相交于A、B和C、D。
求证:AB=CD分析: 联想到“角平分线的性质”,作弦心距OM、ON, 证明: 作 , 垂足分别为M 、 N 。.PABECDF要证AB=CD ,只需证OM=ONOzxxkw.如图,P点在圆上,PB=PD吗?
P点在圆内,AB=CD吗?思考:PBEDFO3、如图,BC为⊙O的直径,OA是⊙O的半径,弦BE∥OA。
求证:AC=AE⌒ ⌒圆心角定理:在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦相等,所对的弦的弦心距相等.zxxkw
同课章节目录
