江苏省盐城市亭湖新区实验学校苏科版八年级数学上册课件:6-6一次函数、一元一次方程和一元一次不等式 (共12张PPT)
文档属性
| 名称 | 江苏省盐城市亭湖新区实验学校苏科版八年级数学上册课件:6-6一次函数、一元一次方程和一元一次不等式 (共12张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 134.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-12-03 00:00:00 | ||
图片预览




文档简介
课件12张PPT。6.6 一次函数、一元一次方程
与一元一次不等式知识回顾 1.我们已经学习了平面直角坐标系 ,请同学们回顾一下: 对点P(x,y),当y=0、y>0 、y<0
时,点P分别位于坐标平面内什么位置?
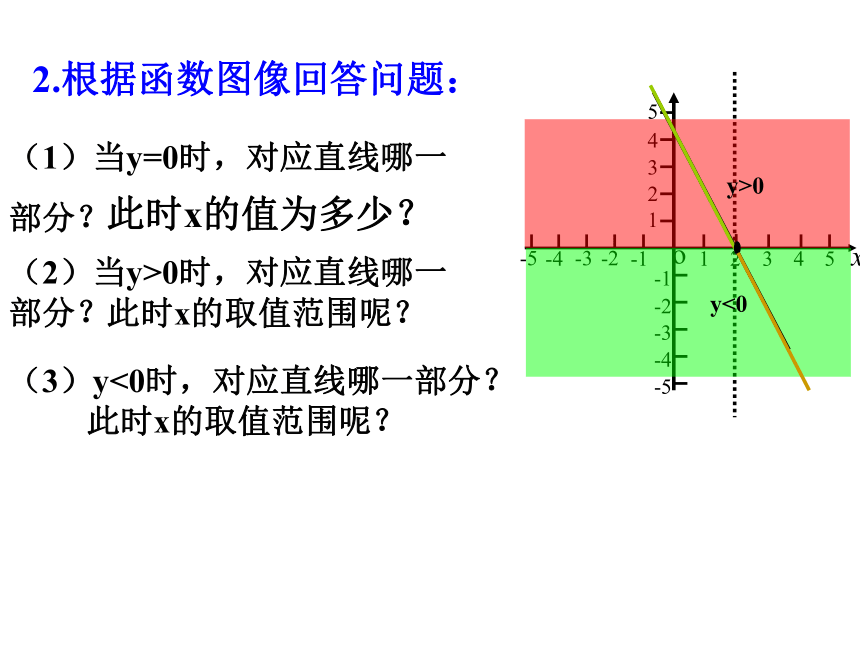
①当y=0时:②当y>0时:y y>0 y<0点P在x轴上;点P在x轴上方;点P在x轴下方.③当y<0时:2.根据函数图像回答问题:
(3)y<0时,对应直线哪一部分?
(1)当y=0时,对应直线哪一
部分?此时x的值为多少?此时x的取值范围呢?此时x的取值范围呢?
(2)当y>0时,对应直线哪一
部分? 问题1:一根长25cm的弹簧,一端固定,另一端挂物体. 在弹簧伸长后的长度不超过35cm的限度内,每挂1kg质量的物体,弹簧伸长0.5cm,如果所挂物体的质量是x kg,弹簧的长度是y cm.新知探索(1)写出y与x之间的函数关系式;
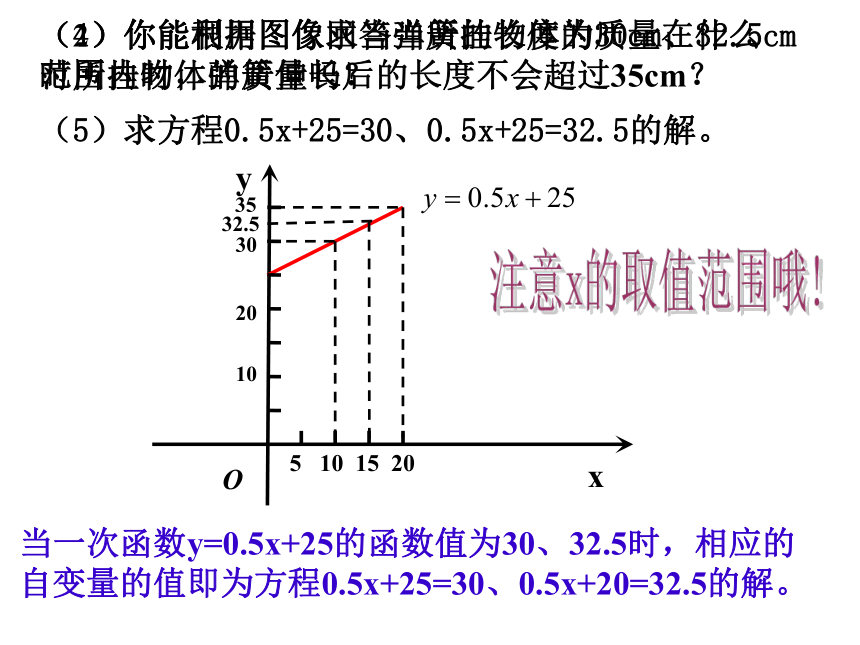
(2)当所挂物体的质量在什么范围内时,弹簧伸长后的长度不会超过35cm?
(3)画出此函数图像。
xy5 10 15 20 O102030当一次函数y=0.5x+25的函数值为30、32.5时,相应的自变量的值即为方程0.5x+25=30、0.5x+20=32.5的解。(4)你能利用图像求当弹簧的长度为30cm、32.5cm时所挂物体的质量吗?(5)求方程0.5x+25=30、0.5x+25=32.5的解。35注意x的取值范围哦!(2)你能根据图像回答当所挂物体的质量在什么范围内时,弹簧伸长后的长度不会超过35cm?
问题2:已知函数y=2x+4的图像如下,试根据函数图 像回答下面的问题: (1)当x为何值时,y=0? (2)当x在什么范围内时,y>0? y=2x+4还有其它方法吗?一般地,一元一次方程kx+b=0的解就是一次函数y=kx+b的图象与x轴交点的横坐标.巩固练习:x取什么值时,函数y= - 2(x+1)+4的值是正数?负数?等于2?2. 已知:一次函数 y=0.8x-2 与x轴的交点为(2.5,0),你能说出方程 0.8x-2=0 的解吗?
3. 已知:一次函数y=kx+b的图象与x轴交点的坐标为(2,0)那么一元一次方程kx+b=0的解
是x=_____.一般地,一元一次方程kx+b=0的解就是
一次函数y=kx+b的图象与x轴交点的横坐标.4.一次函数 y=-x+2 的图象如图所示,你能说出 -x+2<0 的解集吗?解集是 x>2.Oxyy=-x+2225.一次函数 y=kx+b 的图象如图所示,你能说出 kx+b<0 的解集吗?Oxyy=kx+b-4解集是 x< -4. 一辆汽车行驶35km后,驶入高速公路,并以105km/h的速度匀速行驶了xh.拓展延伸:试根据上述情景,提出一些问题,并用一次函数、一元一次方程或一元一次不等式求解。这节课你收获了什么?
(1)x取何值时,2x-4>0?
(2)x取何值时,-2x+8>0?
(3)x取何值时,2x-4>0与
-2x+8>0同时成立?选做题:已知函数y1=2x-4与y2=-2x+8的图像,观察图像并回答问题:(4)求函数y1=2x-4与y2=-2x+8的图像与x轴所围成的三角形的面积?
与一元一次不等式知识回顾 1.我们已经学习了平面直角坐标系 ,请同学们回顾一下: 对点P(x,y),当y=0、y>0 、y<0
时,点P分别位于坐标平面内什么位置?
①当y=0时:②当y>0时:y y>0 y<0点P在x轴上;点P在x轴上方;点P在x轴下方.③当y<0时:2.根据函数图像回答问题:
(3)y<0时,对应直线哪一部分?
(1)当y=0时,对应直线哪一
部分?此时x的值为多少?此时x的取值范围呢?此时x的取值范围呢?
(2)当y>0时,对应直线哪一
部分? 问题1:一根长25cm的弹簧,一端固定,另一端挂物体. 在弹簧伸长后的长度不超过35cm的限度内,每挂1kg质量的物体,弹簧伸长0.5cm,如果所挂物体的质量是x kg,弹簧的长度是y cm.新知探索(1)写出y与x之间的函数关系式;
(2)当所挂物体的质量在什么范围内时,弹簧伸长后的长度不会超过35cm?
(3)画出此函数图像。
xy5 10 15 20 O102030当一次函数y=0.5x+25的函数值为30、32.5时,相应的自变量的值即为方程0.5x+25=30、0.5x+20=32.5的解。(4)你能利用图像求当弹簧的长度为30cm、32.5cm时所挂物体的质量吗?(5)求方程0.5x+25=30、0.5x+25=32.5的解。35注意x的取值范围哦!(2)你能根据图像回答当所挂物体的质量在什么范围内时,弹簧伸长后的长度不会超过35cm?
问题2:已知函数y=2x+4的图像如下,试根据函数图 像回答下面的问题: (1)当x为何值时,y=0? (2)当x在什么范围内时,y>0? y=2x+4还有其它方法吗?一般地,一元一次方程kx+b=0的解就是一次函数y=kx+b的图象与x轴交点的横坐标.巩固练习:x取什么值时,函数y= - 2(x+1)+4的值是正数?负数?等于2?2. 已知:一次函数 y=0.8x-2 与x轴的交点为(2.5,0),你能说出方程 0.8x-2=0 的解吗?
3. 已知:一次函数y=kx+b的图象与x轴交点的坐标为(2,0)那么一元一次方程kx+b=0的解
是x=_____.一般地,一元一次方程kx+b=0的解就是
一次函数y=kx+b的图象与x轴交点的横坐标.4.一次函数 y=-x+2 的图象如图所示,你能说出 -x+2<0 的解集吗?解集是 x>2.Oxyy=-x+2225.一次函数 y=kx+b 的图象如图所示,你能说出 kx+b<0 的解集吗?Oxyy=kx+b-4解集是 x< -4. 一辆汽车行驶35km后,驶入高速公路,并以105km/h的速度匀速行驶了xh.拓展延伸:试根据上述情景,提出一些问题,并用一次函数、一元一次方程或一元一次不等式求解。这节课你收获了什么?
(1)x取何值时,2x-4>0?
(2)x取何值时,-2x+8>0?
(3)x取何值时,2x-4>0与
-2x+8>0同时成立?选做题:已知函数y1=2x-4与y2=-2x+8的图像,观察图像并回答问题:(4)求函数y1=2x-4与y2=-2x+8的图像与x轴所围成的三角形的面积?
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
