六年级下册数学 人教版第六单元 比和比例课件(共20张PPT)
文档属性
| 名称 | 六年级下册数学 人教版第六单元 比和比例课件(共20张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-24 14:27:04 | ||
图片预览



文档简介
(共20张PPT)
人教版数学 六年级下册 第六单元 总复习
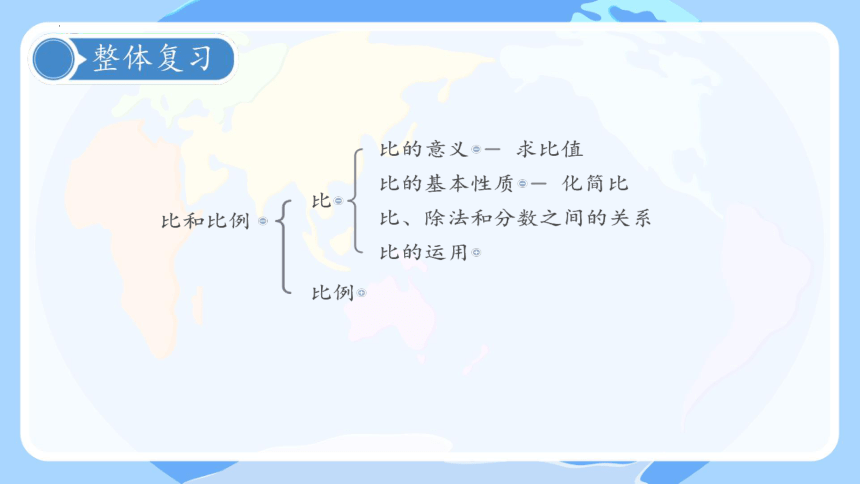
比和比例
1.你能说一说比的意义、各部分名称、基本性质的概念吗?
2.你能说一说求比值和化简比的意义和方法吗?
3.你能说一说比例的意义、各部分名称、基本性质的概念吗?
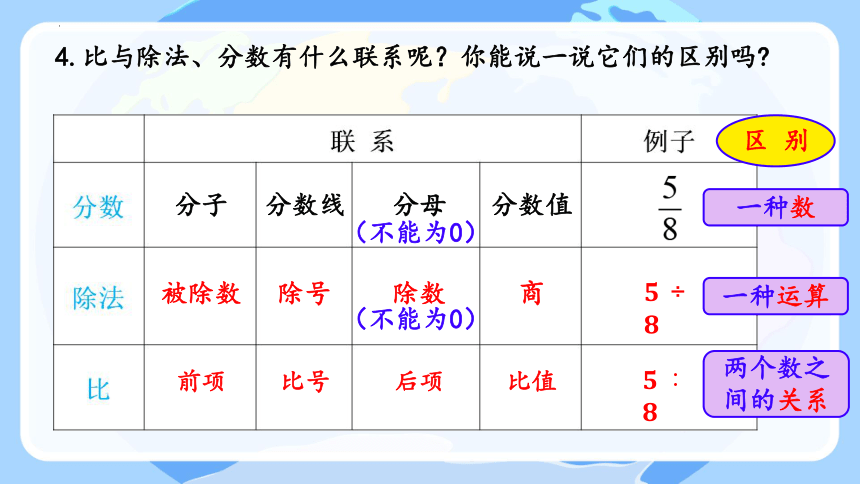
4.比与除法、分数有什么联系呢?你能说一说它们的区别吗
5.你是怎样判断两种相关联的量是正比例关系还是反比例关系?
6.你是怎样解答按比分配的应用题的?
7.你能说一说有关比例尺的知识有哪些?
8.你能总结出“用正反比例知识解决问题”的解题步骤吗?
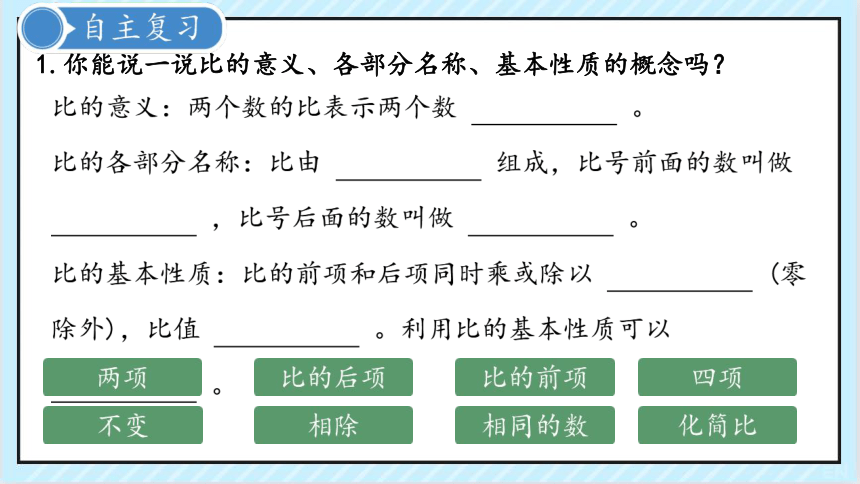
1.你能说一说比的意义、各部分名称、基本性质的概念吗?
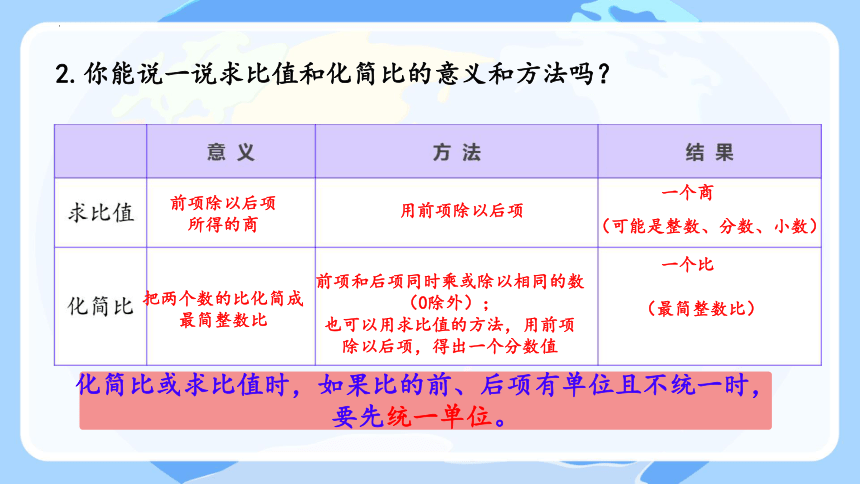
前项除以后项
所得的商
把两个数的比化简成
最简整数比
用前项除以后项
前项和后项同时乘或除以相同的数
(0除外);
也可以用求比值的方法,用前项
除以后项,得出一个分数值
一个商
(可能是整数、分数、小数)
一个比
(最简整数比)
化简比或求比值时,如果比的前、后项有单位且不统一时,要先统一单位。
2.你能说一说求比值和化简比的意义和方法吗?
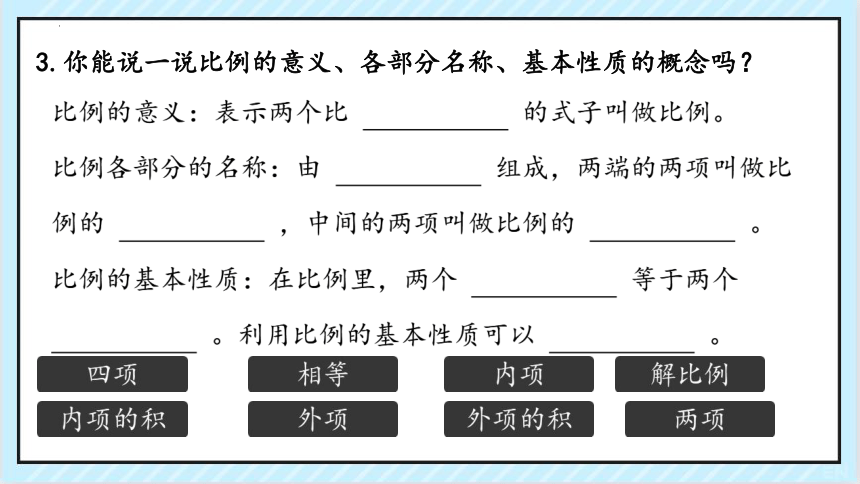
3.你能说一说比例的意义、各部分名称、基本性质的概念吗?
4.比与除法、分数有什么联系呢?你能说一说它们的区别吗
分子
分数线
分母
分数值
被除数
除数
除号
商
÷
前项
比号
后项
比值
∶
(不能为0)
(不能为0)
一种数
一种运算
两个数之间的关系
区 别
都是两个相关联的量,一种量随着另一种量变化。
变化的方向相同
变化的方向相反
一种量扩大(缩小),
另一种量也扩大(缩小)
一种量扩大(缩小),
另一种量反而缩小(扩大)
相对应的两个数的
比值(商)是一定的
相对应的两个数的
乘积是一定的
一条直线
一条曲线
5.你是怎样判断两种相关联的量是正比例关系还是反比例关系?
课本P85.2
判断下面各题中的两个量是否成正比例或反比例关系?
6.你是怎样解答按比分配的应用题的?
15000÷(2+3)
=15000÷5
=3000(元)
3000×2=6000(元)
答:其中用于储蓄的钱是6000元。
7.你能说一说有关比例尺的知识有哪些?
比例尺的分类
同一幅地图上,量得甲、乙两地的直线距离是20cm,甲、丙两地的直线距离是12 cm。如果甲、乙两地的实际距离是1600 km,那么甲、丙两地的实际距离是多少?
解:设甲、丙两地的实际距离是x cm。
12∶x=1∶8000000
x=96000000
96000000cm=960km
答:甲、丙两地的实际距离是960千米。
在比例尺是1:3000000的地图上量得甲乙两地的图上距离是9厘米,客车和货车同时从两地出发相向而行,3小时相遇,已知两车的速度之比是4:5,客车和货车的每小时分别行驶多少km?
答:客车每小时行驶40km/h,货车每小时行驶50km/h。
8.你能总结出“用正反比例知识解决问题”的解题步骤吗?
一审(审题意,找不变量,判断题目中两种相关联的量是成正比例(比值一定)还是反比例(乘积一定))
二找(找相等的数量关系,列出数量关系式)
三设(设未知量为x,并列出比例)
四解(解比例)
五答(用自己熟练的方法来检验并作答)
2.一个办公室原来平均每天用电100千瓦时。改用节能灯后,每天平均节约了25%。原来10天的用电量现在多用多少天?
1.修一条长300米的公路,3天修了75米,照这样计算,余下的要几天才能修完?
3.一辆汽车从甲地到乙地,计划每小时行50千米,6小时到达。实际3小时行了180千米,照这样的速度,行完全程要几小时?(用正反两种比例解答)
2.本节课你的学习榜样是谁?
1.你有什么收获和疑问?
人教版数学 六年级下册 第六单元 总复习
比和比例
1.你能说一说比的意义、各部分名称、基本性质的概念吗?
2.你能说一说求比值和化简比的意义和方法吗?
3.你能说一说比例的意义、各部分名称、基本性质的概念吗?
4.比与除法、分数有什么联系呢?你能说一说它们的区别吗
5.你是怎样判断两种相关联的量是正比例关系还是反比例关系?
6.你是怎样解答按比分配的应用题的?
7.你能说一说有关比例尺的知识有哪些?
8.你能总结出“用正反比例知识解决问题”的解题步骤吗?
1.你能说一说比的意义、各部分名称、基本性质的概念吗?
前项除以后项
所得的商
把两个数的比化简成
最简整数比
用前项除以后项
前项和后项同时乘或除以相同的数
(0除外);
也可以用求比值的方法,用前项
除以后项,得出一个分数值
一个商
(可能是整数、分数、小数)
一个比
(最简整数比)
化简比或求比值时,如果比的前、后项有单位且不统一时,要先统一单位。
2.你能说一说求比值和化简比的意义和方法吗?
3.你能说一说比例的意义、各部分名称、基本性质的概念吗?
4.比与除法、分数有什么联系呢?你能说一说它们的区别吗
分子
分数线
分母
分数值
被除数
除数
除号
商
÷
前项
比号
后项
比值
∶
(不能为0)
(不能为0)
一种数
一种运算
两个数之间的关系
区 别
都是两个相关联的量,一种量随着另一种量变化。
变化的方向相同
变化的方向相反
一种量扩大(缩小),
另一种量也扩大(缩小)
一种量扩大(缩小),
另一种量反而缩小(扩大)
相对应的两个数的
比值(商)是一定的
相对应的两个数的
乘积是一定的
一条直线
一条曲线
5.你是怎样判断两种相关联的量是正比例关系还是反比例关系?
课本P85.2
判断下面各题中的两个量是否成正比例或反比例关系?
6.你是怎样解答按比分配的应用题的?
15000÷(2+3)
=15000÷5
=3000(元)
3000×2=6000(元)
答:其中用于储蓄的钱是6000元。
7.你能说一说有关比例尺的知识有哪些?
比例尺的分类
同一幅地图上,量得甲、乙两地的直线距离是20cm,甲、丙两地的直线距离是12 cm。如果甲、乙两地的实际距离是1600 km,那么甲、丙两地的实际距离是多少?
解:设甲、丙两地的实际距离是x cm。
12∶x=1∶8000000
x=96000000
96000000cm=960km
答:甲、丙两地的实际距离是960千米。
在比例尺是1:3000000的地图上量得甲乙两地的图上距离是9厘米,客车和货车同时从两地出发相向而行,3小时相遇,已知两车的速度之比是4:5,客车和货车的每小时分别行驶多少km?
答:客车每小时行驶40km/h,货车每小时行驶50km/h。
8.你能总结出“用正反比例知识解决问题”的解题步骤吗?
一审(审题意,找不变量,判断题目中两种相关联的量是成正比例(比值一定)还是反比例(乘积一定))
二找(找相等的数量关系,列出数量关系式)
三设(设未知量为x,并列出比例)
四解(解比例)
五答(用自己熟练的方法来检验并作答)
2.一个办公室原来平均每天用电100千瓦时。改用节能灯后,每天平均节约了25%。原来10天的用电量现在多用多少天?
1.修一条长300米的公路,3天修了75米,照这样计算,余下的要几天才能修完?
3.一辆汽车从甲地到乙地,计划每小时行50千米,6小时到达。实际3小时行了180千米,照这样的速度,行完全程要几小时?(用正反两种比例解答)
2.本节课你的学习榜样是谁?
1.你有什么收获和疑问?
