专题六:数与代数《比和比例》复习课件(共44张PPT)六年级数学下学期期末核心考点集训(人教版)
文档属性
| 名称 | 专题六:数与代数《比和比例》复习课件(共44张PPT)六年级数学下学期期末核心考点集训(人教版) |  | |
| 格式 | pptx | ||
| 文件大小 | 486.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-25 16:12:33 | ||
图片预览









文档简介
(共44张PPT)
专题06:数与代数——比和比例
期末专项考点复习
人教版·六年级下册
2023-2024学年
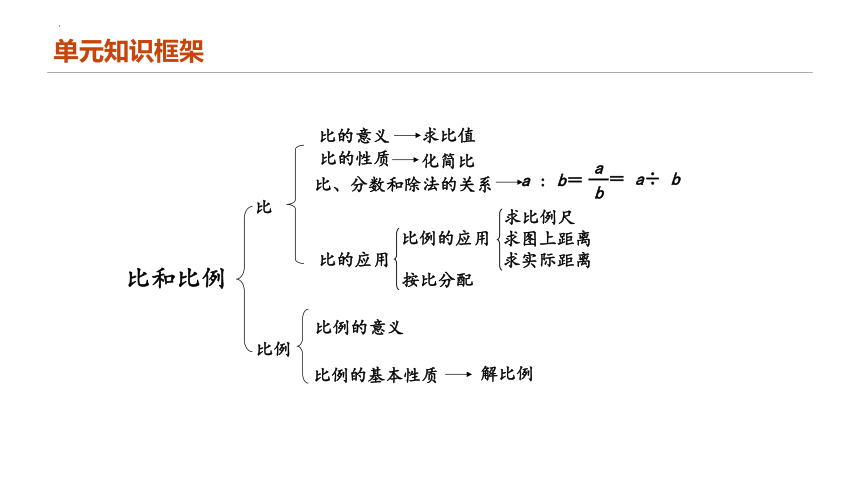
单元知识框架
比例
比和比例
比
求比值
比的性质
比的意义
化简比
比、分数和除法的关系
比的应用
a : b=
b
a
= a÷ b
比例的应用
按比分配
求比例尺
求图上距离
求实际距离
比例的意义
比例的基本性质
解比例
www.islide.cc考点目录CONTENT比的概念比的基本性质按比例分配问题按比例分配问题考点01考点02考点03考点04考点05比例的基本性质考点06考点07比例尺正比例和反比例比的概念
/01
知识梳理
1、比的概念
●比的意义
两个数相除又叫做两个数的比。
●比值的概念
比的前项除以后项所得的商,叫做比值。
例如: 5÷6 可记作 5∶6。
例如:5÷6 = →就是5:6的比值。
——是借助于除法的概念建立的。
知识梳理
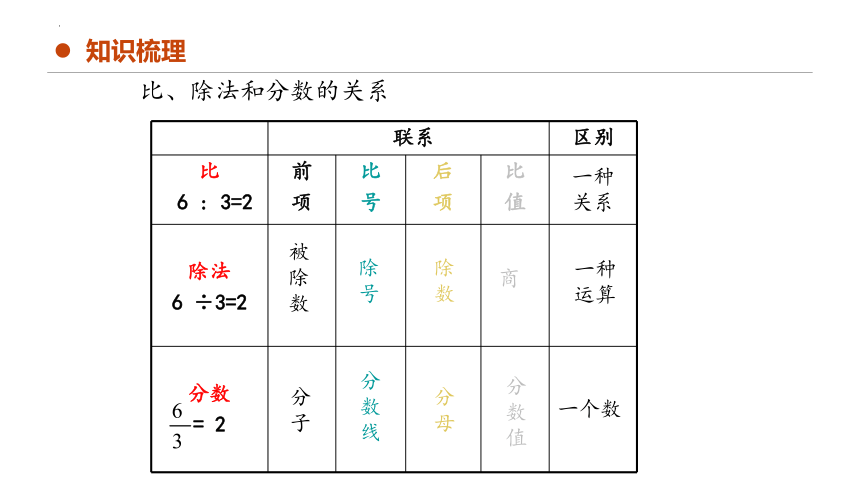
比与除法和分数的关系
比的前项相当于分数的分子和除式中的被除数;
比的后项相当于分数的分母和除式中的除数;
比值相当于分数的分数值和除式中的商
a :b = a÷b = (b≠0)
知识梳理
联系 区别
比 6 : 3=2 前 项 比 号 后 项 比 值
除法 6 ÷3=2
分数 = 2
比、除法和分数的关系
一种
关系
被除数
分子
除号
分数线
除数
分母
商
分
数
值
一种
运算
一个数
知识梳理
比值的意义:
同类数量的比值:
不同类数量的比值:
能加单位
不能加单位
例:两辆汽车在公路上行驶,甲车行了75千米,耗油10升,乙车行了60千米,耗油9升。
75千米:10升=7.5千米/升表示甲车每升汽油能行7.5千米。
60千米:75千米= ,表示乙车行的路程是甲车的 。
——产生新的量。
表示倍数关系或几分之几。
典型例题
在含盐5%的盐水中,盐与水的质量比写成最简整数比是( )。
分析:在5%的盐水中盐与盐水的比是5:100,盐与水的比是5:(100-5)=5:95=1:19。
解答:1:19。
跟踪练习
三个数的平均数是13,这三个数的比是1/2:2/3:1,这三个数中最大的是( )。
分析:三个数的比是1/2:2/3:1,化简为3:4:6,则最大的数占总数的 6/3+4+6,三个数的总数是13x3=39,所以三个数中最大的数是39x6/ 3+4+6 =18。
解答:18。
比的基本性质
/02
知识梳理
比的基本性质:
比的前项和后项同时乘或除以相同的数(0除外),比值不变。这叫做比的基本性质。
利用商不变性质,我们可以进行除法的简算,也可以把小数除法变为整数除法计算。根据分数的基本性质,我们可以把分数约分成最简分数。
4︰6
=
2︰3
前项、后项同时除以2
应用比的基本性质,我们可以把比化成最简整数比。
2
3
前、后项必须是整数,而且互质.
知识梳理
一般方法 结果
求比值
化简比
求比值和化简比的区别
根据比的意义,用前项除以后项。
是一个数,可以是整数、小数或分数。
根据比的基本性质,把比的前项和后项同时乘或除以相同的数(0除外)。
是一个比,它的前项和后项是互质数(两个互质的整数比)。
知识梳理
归纳化简比的方法:
整数比
最简
整数比
前、后项同时除以
它们的最大公因数
小数比
分数比
前、后项同时
扩大相同的倍数
前、后项同时乘上两
个分母的最小公倍数
典型例题
32 : 16
=(32÷16) : (16÷16)
=2 : 1
48 : 40
=(48÷8) : (40÷8)
=6 : 5
怎样化简整数比?
比的前、后项都除以它们的最大公因数→最简比。
整数比
求比值:32 : 16;48 : 40
典型例题
0.15 : 0.3
=(0.15×100) : (0.3×100)
=15 : 30
怎样化简小数比?
比的前、后项都扩大相同的倍数→整数比→最简比。
=(15÷15) : (30÷15)
=1 : 2
0.75︰2
=(0.75×100)︰(2×100)
= (75÷25)︰(200÷25)
= 3︰8
= 75︰200
跟踪练习
怎样化简分数比?
比的前、后项都乘它们分母的最小公倍数→整数比→最简比。
分数比
按比例分配问题
/03
知识梳理
在农业生产和日常生活中,常常需要把一个数量按照一定的比来进行分配。这种分配的方法通常叫做按比例分配。
●特点:
已知总量和部分量的比,求各部分量是多少。
●解题方法:
先求总份数,再求个部分量占总量的几分之几,最后用总量乘以这个几分之几,求出个部分量。
典型例题
2:3
3:7
例:将这两种浓缩液混在一起制成新的清洁液,那么这种新的清洁液中浓缩液是清洁液的百分之几?(百分号前保留一位小数)
250ml 500ml
浓缩液是清洁液的百分之几?
250 x
+ 500 x
=150(ml)
150÷750×100% ≈33.3%
250+500=750(ml)
跟踪练习
例:3克的蚂蚁能搬动45克的物体;3吨的大象能拉动4.5吨的物体,蚂蚁和大象谁的力气大?(要求:用学过的知识说明你的观点,回答要全面)
从物体的重量与动物本身的重量的比或比值看是蚂蚁的力气大,但是如果从动物驮的物体的重量来看是大象的力气大。
3:45 =1:15 或 45:3=15
3:4.5 =1:1.5 4.5:3=1.5
比例的意义
/04
知识梳理
比例的意义:
表示两个比相等的式子叫做比例。
例如:
2.4 ∶1.6 = 60 ∶40
外项
内项
组成比例的四个数,叫做比例的项。两端的两项叫做比例的外项,中间的两项叫做比例的内项。
( )
内项
( )
( )
( )
外项
外项
内项
典型例题
例:将上题中的平行四边形按照一定比例缩小,画在平面图上,量得图上平行四边形的底是3厘米,高是2厘米。那么图上平行四边形的底与实际底的比是( ),我们把这个比叫做( );这个比还和( )和( )的比相等,组成的比例是( )。
1.2m
0.8m
1:40
比例尺
图上的高
实际的高
3:120=2:80
跟踪练习
两个长方形重叠在一起,(如右图),重叠部分
的面积是大长方形面积的 ,是小长方形面积的 ,那么
大长方形的面积S1和小长方形面积S2的比是( )
长方形面积的 =
小长方形面积的
S1×
= S2 ×
S1:S2 =12:5
12:5
比例的基本性质
/05
知识梳理
在比例里,两个外项的积等于两个内项的积,这叫做比例的基本性质。
比例的基本性质:
用字母表示为:
如果a:b=c:d,那么ad=bc。
典型例题
【例】甲、乙两数的比是3:7,如果甲数加上6,要使比值不变,乙数应加上多少
【解析】甲、乙两数的比是3:7,如果甲数加上6后,甲数为6+3=9,可知甲数由原来的3到现在的9,扩大到原来的3倍,要使比值不变,根据比的基本性质,比的后项也应扩大到原来的3倍,所以乙数也应扩大到原来的3倍,即7×3=21,因此乙数应加上21-7=14。
【解答】 (3+6)÷3=33×7-7=14
跟踪练习
例:在一个比例里,两个外项为互倒数,其中
一个内项是 ,另一个内项是( )。
当x=( )时,0.9∶x和3∶2能组成比例。
6
比例尺
/06
知识梳理
比例尺
数值比例尺
线段比例尺
比的形式
分数形式
图上距离
实际距离
=
1 :100
( )
0 100 200 300千米
实质上是一种比,是图上距离与实际距离的比。
典型例题
【例】在一幅图上距离3cm代表实际距离360km的地图上,量得A,B两地相距8cm,A、B两地的实际距离是多少千米
【解析】本题考查求比例尺及根据比例尺和图上距离求实际距离。先求出这幅地图的比例尺,再求出A,B两地的实际距离。
【解答】
3cm:360km
=3cm:36000000cm
=1:12000000
跟踪练习
在一幅比例尺为1:500的地图上,量得一间教室的长是3cm,宽是2cm,求这间教室的实际占地面积。
【解答】
正比例和反比例
/07
知识梳理
正比例
两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比的比值(商)一定,这两种量就叫做成正比例的量,它们之间的关系叫做正比例关系。
如果用x和y表示两种相关联的量,用k表示它们的比值,那么上面这种数量关系式可以用 (一定) 来表示。
反比例
两种相关联的量,一种量变化,另一种量也随着变化 ,如果这两种量中相对应的两个数的乘积一定,这两种量就叫做成反比例的量,它们的关系叫做反比例关系。
如果用x和y表示两种相关联的量,用k表示它们 的乘积,那么上面这种数量关系式可以用xy=k (一定)来表示
典型例题
【例】判断(对的画“√”,错的画“×”)
(1)如果y=8,那么和y成反比例。 ( )
(2)一本书,已经看的页数和未看的页数成正比例。( )
(3)圆的半径和面积不成比例。 ( )
【解答】(1)× (2)× (3)√
【解析】本题考查正比例和反比例的意义。
(l)将y=8 变成 =8可以看出,y和 的比值一定,而不是积一定,所以 和y是成正比例而不是成反比例。
(2)一本书,已看的页数和未看的页数的和一定,不是积一定也不是比值一定,所以不成比例。
(3)虽然圆的半径和面积是两个相关联的量,但它们的积不一定。比值也不一定,所以不成比例。
跟踪练习
下面两种量,是否成比例 如果成比例,成什么比例 并说明理由。
(1)汽车的速度一定,它行驶的路程和时间。
(1) 成正比例
(2)三角形的面积一定,三角形的底和高。
(2) 成反比例
(3)长方形的周长一定,它的长和宽。
(3)不成比例
考点综合练习
1.判断(对的画“√”,错的画“×”)
1.化简比的依据是比例的基本性质。 ( )
2.比值是2的比有无数个。 ( )
3.比的前项和后项同时乘或除以相同的数,比值不变, ( )
4.如果a:b=8:5,那么a=8,b=5。 ( )
5.甲数的 等于乙数的 (甲数、乙数均不为0),则甲数与乙数的比是9:7。( )
【解答】 1.√ 2.√ 3.× 4.× 5.√
考点综合练习
2.小龙今年5岁,小龙的爸爸今年38岁,6年后小龙与爸爸的年龄的最简整数比是多少
【解答】
(6+5):(38+6)=1:4
答:6年后小龙与爸爸的年龄的最简整数比是1:4。
考点综合练习
3.运一批货物,每天运的吨数和需要的天数如下表。
1.写出几组这两个量中对应的两个数的积,并比较积的大小。
2.这个积表示什么
3.表中相关联的两个量成反比例吗 为什么
【解答】
1. 300×1=300 150×2=300 100×3=300 积相等
2.答:积表示这批货物的总吨数。
3.答:成反比例。因为对应两个量的积一定。
每天运的吨数 300 150 100 75 60 50
需要的天数 1 2 3 4 5 6
考点综合练习
4.芳芳家新买了一辆家用小轿车,其油箱可以装40L油,小轿车行驶一段路程后,油箱中的剩余油量与行驶时间的关系如右图:
(1)小轿车行驶2小时用去了( )L油。
(2)一箱油够连续行驶( )h。
【解答】(1)10 (2)8
考点综合练习
5.学校将200粒太空种子按2:3:5分配给四、五,六年级同学种植,四、五、六年级各分到太空种子多少粒
【解答】
答:四年级分到太空种子40粒,五年级分到60粒,六年级分到100粒。
考点综合练习
6.在比例尺是1:2500000的地图上,量得甲、乙两城之间的距离是7.2cm。一辆汽车从甲城到乙城,平均每小时行80km,需要多少小时
【解答】
答:需要2.25小时
乘风破浪会有时
直挂云帆济沧海
专题06:数与代数——比和比例
期末专项考点复习
人教版·六年级下册
2023-2024学年
单元知识框架
比例
比和比例
比
求比值
比的性质
比的意义
化简比
比、分数和除法的关系
比的应用
a : b=
b
a
= a÷ b
比例的应用
按比分配
求比例尺
求图上距离
求实际距离
比例的意义
比例的基本性质
解比例
www.islide.cc考点目录CONTENT比的概念比的基本性质按比例分配问题按比例分配问题考点01考点02考点03考点04考点05比例的基本性质考点06考点07比例尺正比例和反比例比的概念
/01
知识梳理
1、比的概念
●比的意义
两个数相除又叫做两个数的比。
●比值的概念
比的前项除以后项所得的商,叫做比值。
例如: 5÷6 可记作 5∶6。
例如:5÷6 = →就是5:6的比值。
——是借助于除法的概念建立的。
知识梳理
比与除法和分数的关系
比的前项相当于分数的分子和除式中的被除数;
比的后项相当于分数的分母和除式中的除数;
比值相当于分数的分数值和除式中的商
a :b = a÷b = (b≠0)
知识梳理
联系 区别
比 6 : 3=2 前 项 比 号 后 项 比 值
除法 6 ÷3=2
分数 = 2
比、除法和分数的关系
一种
关系
被除数
分子
除号
分数线
除数
分母
商
分
数
值
一种
运算
一个数
知识梳理
比值的意义:
同类数量的比值:
不同类数量的比值:
能加单位
不能加单位
例:两辆汽车在公路上行驶,甲车行了75千米,耗油10升,乙车行了60千米,耗油9升。
75千米:10升=7.5千米/升表示甲车每升汽油能行7.5千米。
60千米:75千米= ,表示乙车行的路程是甲车的 。
——产生新的量。
表示倍数关系或几分之几。
典型例题
在含盐5%的盐水中,盐与水的质量比写成最简整数比是( )。
分析:在5%的盐水中盐与盐水的比是5:100,盐与水的比是5:(100-5)=5:95=1:19。
解答:1:19。
跟踪练习
三个数的平均数是13,这三个数的比是1/2:2/3:1,这三个数中最大的是( )。
分析:三个数的比是1/2:2/3:1,化简为3:4:6,则最大的数占总数的 6/3+4+6,三个数的总数是13x3=39,所以三个数中最大的数是39x6/ 3+4+6 =18。
解答:18。
比的基本性质
/02
知识梳理
比的基本性质:
比的前项和后项同时乘或除以相同的数(0除外),比值不变。这叫做比的基本性质。
利用商不变性质,我们可以进行除法的简算,也可以把小数除法变为整数除法计算。根据分数的基本性质,我们可以把分数约分成最简分数。
4︰6
=
2︰3
前项、后项同时除以2
应用比的基本性质,我们可以把比化成最简整数比。
2
3
前、后项必须是整数,而且互质.
知识梳理
一般方法 结果
求比值
化简比
求比值和化简比的区别
根据比的意义,用前项除以后项。
是一个数,可以是整数、小数或分数。
根据比的基本性质,把比的前项和后项同时乘或除以相同的数(0除外)。
是一个比,它的前项和后项是互质数(两个互质的整数比)。
知识梳理
归纳化简比的方法:
整数比
最简
整数比
前、后项同时除以
它们的最大公因数
小数比
分数比
前、后项同时
扩大相同的倍数
前、后项同时乘上两
个分母的最小公倍数
典型例题
32 : 16
=(32÷16) : (16÷16)
=2 : 1
48 : 40
=(48÷8) : (40÷8)
=6 : 5
怎样化简整数比?
比的前、后项都除以它们的最大公因数→最简比。
整数比
求比值:32 : 16;48 : 40
典型例题
0.15 : 0.3
=(0.15×100) : (0.3×100)
=15 : 30
怎样化简小数比?
比的前、后项都扩大相同的倍数→整数比→最简比。
=(15÷15) : (30÷15)
=1 : 2
0.75︰2
=(0.75×100)︰(2×100)
= (75÷25)︰(200÷25)
= 3︰8
= 75︰200
跟踪练习
怎样化简分数比?
比的前、后项都乘它们分母的最小公倍数→整数比→最简比。
分数比
按比例分配问题
/03
知识梳理
在农业生产和日常生活中,常常需要把一个数量按照一定的比来进行分配。这种分配的方法通常叫做按比例分配。
●特点:
已知总量和部分量的比,求各部分量是多少。
●解题方法:
先求总份数,再求个部分量占总量的几分之几,最后用总量乘以这个几分之几,求出个部分量。
典型例题
2:3
3:7
例:将这两种浓缩液混在一起制成新的清洁液,那么这种新的清洁液中浓缩液是清洁液的百分之几?(百分号前保留一位小数)
250ml 500ml
浓缩液是清洁液的百分之几?
250 x
+ 500 x
=150(ml)
150÷750×100% ≈33.3%
250+500=750(ml)
跟踪练习
例:3克的蚂蚁能搬动45克的物体;3吨的大象能拉动4.5吨的物体,蚂蚁和大象谁的力气大?(要求:用学过的知识说明你的观点,回答要全面)
从物体的重量与动物本身的重量的比或比值看是蚂蚁的力气大,但是如果从动物驮的物体的重量来看是大象的力气大。
3:45 =1:15 或 45:3=15
3:4.5 =1:1.5 4.5:3=1.5
比例的意义
/04
知识梳理
比例的意义:
表示两个比相等的式子叫做比例。
例如:
2.4 ∶1.6 = 60 ∶40
外项
内项
组成比例的四个数,叫做比例的项。两端的两项叫做比例的外项,中间的两项叫做比例的内项。
( )
内项
( )
( )
( )
外项
外项
内项
典型例题
例:将上题中的平行四边形按照一定比例缩小,画在平面图上,量得图上平行四边形的底是3厘米,高是2厘米。那么图上平行四边形的底与实际底的比是( ),我们把这个比叫做( );这个比还和( )和( )的比相等,组成的比例是( )。
1.2m
0.8m
1:40
比例尺
图上的高
实际的高
3:120=2:80
跟踪练习
两个长方形重叠在一起,(如右图),重叠部分
的面积是大长方形面积的 ,是小长方形面积的 ,那么
大长方形的面积S1和小长方形面积S2的比是( )
长方形面积的 =
小长方形面积的
S1×
= S2 ×
S1:S2 =12:5
12:5
比例的基本性质
/05
知识梳理
在比例里,两个外项的积等于两个内项的积,这叫做比例的基本性质。
比例的基本性质:
用字母表示为:
如果a:b=c:d,那么ad=bc。
典型例题
【例】甲、乙两数的比是3:7,如果甲数加上6,要使比值不变,乙数应加上多少
【解析】甲、乙两数的比是3:7,如果甲数加上6后,甲数为6+3=9,可知甲数由原来的3到现在的9,扩大到原来的3倍,要使比值不变,根据比的基本性质,比的后项也应扩大到原来的3倍,所以乙数也应扩大到原来的3倍,即7×3=21,因此乙数应加上21-7=14。
【解答】 (3+6)÷3=33×7-7=14
跟踪练习
例:在一个比例里,两个外项为互倒数,其中
一个内项是 ,另一个内项是( )。
当x=( )时,0.9∶x和3∶2能组成比例。
6
比例尺
/06
知识梳理
比例尺
数值比例尺
线段比例尺
比的形式
分数形式
图上距离
实际距离
=
1 :100
( )
0 100 200 300千米
实质上是一种比,是图上距离与实际距离的比。
典型例题
【例】在一幅图上距离3cm代表实际距离360km的地图上,量得A,B两地相距8cm,A、B两地的实际距离是多少千米
【解析】本题考查求比例尺及根据比例尺和图上距离求实际距离。先求出这幅地图的比例尺,再求出A,B两地的实际距离。
【解答】
3cm:360km
=3cm:36000000cm
=1:12000000
跟踪练习
在一幅比例尺为1:500的地图上,量得一间教室的长是3cm,宽是2cm,求这间教室的实际占地面积。
【解答】
正比例和反比例
/07
知识梳理
正比例
两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比的比值(商)一定,这两种量就叫做成正比例的量,它们之间的关系叫做正比例关系。
如果用x和y表示两种相关联的量,用k表示它们的比值,那么上面这种数量关系式可以用 (一定) 来表示。
反比例
两种相关联的量,一种量变化,另一种量也随着变化 ,如果这两种量中相对应的两个数的乘积一定,这两种量就叫做成反比例的量,它们的关系叫做反比例关系。
如果用x和y表示两种相关联的量,用k表示它们 的乘积,那么上面这种数量关系式可以用xy=k (一定)来表示
典型例题
【例】判断(对的画“√”,错的画“×”)
(1)如果y=8,那么和y成反比例。 ( )
(2)一本书,已经看的页数和未看的页数成正比例。( )
(3)圆的半径和面积不成比例。 ( )
【解答】(1)× (2)× (3)√
【解析】本题考查正比例和反比例的意义。
(l)将y=8 变成 =8可以看出,y和 的比值一定,而不是积一定,所以 和y是成正比例而不是成反比例。
(2)一本书,已看的页数和未看的页数的和一定,不是积一定也不是比值一定,所以不成比例。
(3)虽然圆的半径和面积是两个相关联的量,但它们的积不一定。比值也不一定,所以不成比例。
跟踪练习
下面两种量,是否成比例 如果成比例,成什么比例 并说明理由。
(1)汽车的速度一定,它行驶的路程和时间。
(1) 成正比例
(2)三角形的面积一定,三角形的底和高。
(2) 成反比例
(3)长方形的周长一定,它的长和宽。
(3)不成比例
考点综合练习
1.判断(对的画“√”,错的画“×”)
1.化简比的依据是比例的基本性质。 ( )
2.比值是2的比有无数个。 ( )
3.比的前项和后项同时乘或除以相同的数,比值不变, ( )
4.如果a:b=8:5,那么a=8,b=5。 ( )
5.甲数的 等于乙数的 (甲数、乙数均不为0),则甲数与乙数的比是9:7。( )
【解答】 1.√ 2.√ 3.× 4.× 5.√
考点综合练习
2.小龙今年5岁,小龙的爸爸今年38岁,6年后小龙与爸爸的年龄的最简整数比是多少
【解答】
(6+5):(38+6)=1:4
答:6年后小龙与爸爸的年龄的最简整数比是1:4。
考点综合练习
3.运一批货物,每天运的吨数和需要的天数如下表。
1.写出几组这两个量中对应的两个数的积,并比较积的大小。
2.这个积表示什么
3.表中相关联的两个量成反比例吗 为什么
【解答】
1. 300×1=300 150×2=300 100×3=300 积相等
2.答:积表示这批货物的总吨数。
3.答:成反比例。因为对应两个量的积一定。
每天运的吨数 300 150 100 75 60 50
需要的天数 1 2 3 4 5 6
考点综合练习
4.芳芳家新买了一辆家用小轿车,其油箱可以装40L油,小轿车行驶一段路程后,油箱中的剩余油量与行驶时间的关系如右图:
(1)小轿车行驶2小时用去了( )L油。
(2)一箱油够连续行驶( )h。
【解答】(1)10 (2)8
考点综合练习
5.学校将200粒太空种子按2:3:5分配给四、五,六年级同学种植,四、五、六年级各分到太空种子多少粒
【解答】
答:四年级分到太空种子40粒,五年级分到60粒,六年级分到100粒。
考点综合练习
6.在比例尺是1:2500000的地图上,量得甲、乙两城之间的距离是7.2cm。一辆汽车从甲城到乙城,平均每小时行80km,需要多少小时
【解答】
答:需要2.25小时
乘风破浪会有时
直挂云帆济沧海
