专题六:数与代数《数的运算》复习课件(共30张PPT)六年级数学下学期期末核心考点集训(人教版)
文档属性
| 名称 | 专题六:数与代数《数的运算》复习课件(共30张PPT)六年级数学下学期期末核心考点集训(人教版) |  | |
| 格式 | pptx | ||
| 文件大小 | 508.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-25 15:51:57 | ||
图片预览









文档简介
(共30张PPT)
专题06:数与代数——数的运算
期末专项考点复习
人教版·六年级下册
2023-2024学年
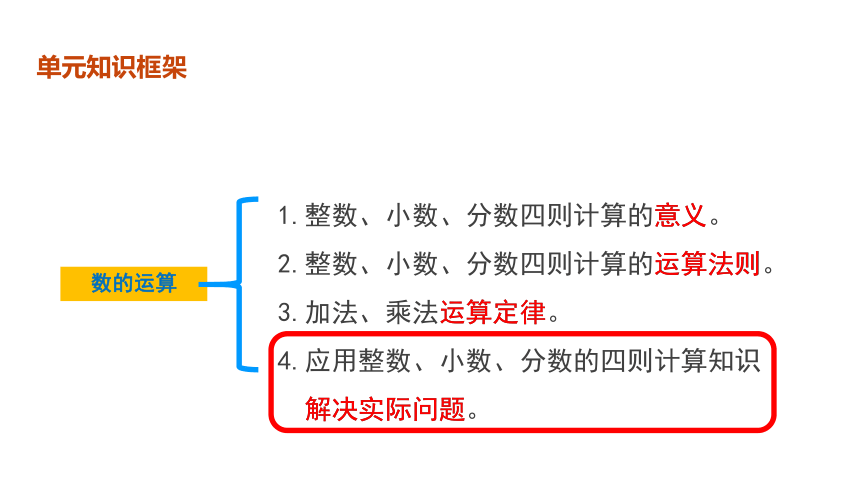
1.整数、小数、分数四则计算的意义。
2.整数、小数、分数四则计算的运算法则。
3.加法、乘法运算定律。
4.应用整数、小数、分数的四则计算知识
解决实际问题。
数的运算
意义
运算定律
解决实际问题
运算法则
单元知识框架
www.islide.cc考点目录CONTENT四则运算的意义四则运算法则运算定律四则混合运算的顺序考点01考点02考点03考点04考点05四则运算的意义
/01
知识梳理
1.整数加法:
(把两个数合并成一个数)的运算叫做加法。在加。法里,相加的数叫做加数,加得的数叫做和。加数是部分数,和是总数。
2.整数减法:
已知(两个加数的和与其中的一个加数),求(另一个加数)的运算叫做减法。被减数是总数,减数和差分别是部分数。加法和减法互为逆运算。
被减数-减数=差
被减数=(差+减数)
减数=(被减数-差)
知识梳理
3.整数乘法:
求(几个相同加数的和)的简便运算叫做乘法。在乘法里,相同的加数和相同加数的个数都叫做因数。相同加数的和叫做积。在乘法里,0和任何数相乘都得0。1和任何数相乘都得任何数。
一个因数×一个因数 =积。
一个因数=(积÷另一个因数)。
4. 整数除法:
已知(两个因数的积与其中一个因数),求(另一个因数的运算)叫做除法。在除法里,已知的积叫做被除数,已知的一个因数叫做除数,所求的因数叫做商。乘法和除法互为逆运算。在除法里,0不能做除数。因为0和任何数相乘都得0,所以任何一个数除以0,均得不到一个确定的商。
被除数÷除数=商
除数=(被除数÷商)
被除数=(商×除数) 。
典型例题
1.下列各算式中,“4”和“5”不能直接相加的算式是( )
A. ①② B. ②③ C.①③ D ②④
A
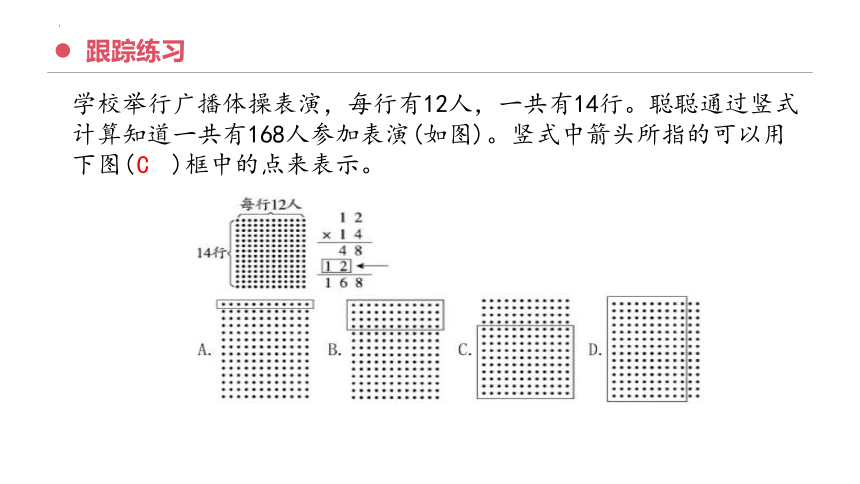
跟踪练习
学校举行广播体操表演,每行有12人,一共有14行。聪聪通过竖式计算知道一共有168人参加表演(如图)。竖式中箭头所指的可以用下图( )框中的点来表示。
C
四则运算法则
/02
知识梳理
1.整数加法:
把两个数合并成一个数的运算叫做加法。
在加法里,相加的数叫做加数,加得的数叫做和。加数是部分数,和是总数。
关系:加数+加数=和
一个加数=和-另一个加数
2.整数减法:
已知两个加数的和与其中的一个加数,求另一个加数的运算叫做减法。
在减法里,已知的和叫做被减数,已知的加数叫做减数,未知的加数叫做差。被减数是总数,减数和差分别是部分数。
关系:被减数-减数=差
差+减数=被减数
注:加法和减法互为逆运算。
知识梳理
3.整数乘法:
求几个相同加数的和的简便运算叫做乘法。
在乘法里,相同的加数和相同加数的个数都叫做因数。相同加数的和叫做积。
关系:
一个因数× 一个因数 =积
一个因数=积÷另一个因数
注:在乘法里,0和任何数相乘都得0;1和任何数相乘都的任何数。
4.整数除法:
已知两个因数的积与其中一个因数,求另一个因数的运算叫做除法。
在除法里,已知的积叫做被除数,已知的一个因数叫做除数,所求的因数叫做商。
关系:
被除数÷除数=商 除数=被除数÷商 被除数=商×除数
注:乘法和除法互为逆运算。
在除法里,0不能做除数。(因为0和任何数相乘都得0,所以任何一个数除以0,均得不到一个确定的商。)
知识梳理
小数加法:
小数加法的意义与整数加法的意义相同。是把两个数合并成一个数的运算。
小数减法:
小数减法的意义与整数减法的意义相同。已知两个加数的和与其中的一个加数,求另一个加数的运算.
小数乘法:
小数乘整数的意义和整数乘法的意义相同,就是求几个相同加数和的简便运算;一个数乘纯小数的意义是求这个数的十分之几、百分之几、千分之几……是多少。
小数除法:
小数除法的意义与整数除法的意义相同,就是已知两个因数的积与其中一个因数,求另一个因数的运算。
知识梳理
分数加法:
分数加法的意义与整数加法的意义相同。是把两个数合并成一个数的运算。
分数减法:
分数减法的意义与整数减法的意义相同。已知两个加数的和与其中的一个加数,求另一个加数的运算。
分数乘法:
分数乘法的意义与整数乘法的意义相同,就是求几个相同加数和的简便运算。
分数除法:
分数除法的意义与整数除法的意义相同。就是已知两个因数的积与其中一个因数,求另一个因数的运算。
典型例题
脱式计算
460-(24+480÷60 ) 750+360÷15×22
(56-32)÷1.5+198 100÷2.5+120 ÷0.6
=460-(24+8)
=460-32
=428
=750+24×22
=750+528
=1278
=24÷1.5+198
=16+198
=214
=40+200
=240
方法提示:
①同级运算,从左向右依次计算。
②如果既有乘除又有加减,先算乘除,再算加减。
③如果有括号,先算括号里面的,再算括号外面的。
跟踪练习
已知算式75x18=1350,在括号里填上合适的数。
750x1.8=( )
135÷7.5 =( )
1.35÷0.18=( )
( )x( )=1350
( )x( )=1350
1800
18
7.5
7500
0.18
0.75
1350
运算定律
/03
知识梳理
1.加法交换律:
两个数相加,交换加数的位置,它们的和不变,即a+b=b+a 。
2.加法结合律:
三个数相加,先把前两个数相加,再加上第三个数;或者先把后两个数相加,再和第一个数相加它们的和不变,即(a+b)+c=a+(b+c) 。
3.乘法交换律:
两个数相乘,交换因数的位置它们的积不变,即a×b=b×a。
4.乘法结合律:
三个数相乘,先把前两个数相乘,再乘以第三个数;或者先把后两个数相乘,再和第一个数相乘,它们的积不变,即(a×b)×c=a×(b×c) 。
5.乘法分配律:
两个数的和与一个数相乘,可以把两个加数分别与这个数相乘再把两个积相加,即(a+b)×c=a×c+b×c 。
典型例题
【例】用简便方法计算。
【解析】这道题应该仔细观察, 有一个因数 ,而 ,也有一个因数 ,后面的25%等于 ,因此利用乘法分配律计算比较简便。
【解答】
跟踪练习
【解答】
运算的顺序
/04
知识梳理
1. 没有括号的混合运算:
同级运算从(左)往(右)依次运算;两级运算先算(乘、除)法,后算(加减)法。
2. 有括号的混合运算:
先算(小括号里面的),再算(中括号里面的),最后算(括号外面的)。
3. 第一级运算:
(加法和减法)叫做第一级运算。第二级运算:(乘法和除法)叫做第二级运算。
4.小数四则运算的运算顺序:
和整数四则运算顺序相同。
5.分数四则运算的运算顺序:
和整数四则运算顺序相同。
典型例题
【解析】本题考查两级运算及含有括号的四则混合运算。
题中既有中括号又有小括号,先算小括号和中括号里面的,再算括号外面的。在计算时不要急于将小数和分数统一,先观察整个算式的结构特征,再根据需要进行转换,灵活运用。
跟踪练习
计算下面各题。
(1)832-36×24÷27 (2)
【解答】
(1)832-36×24÷27
=832-864÷27
=832-32
=800
考点综合练习
1.用简便方法计算。
3.5×9.9+0.35 0.63×101 6.35×12.5-6.35×2.5
=0.35×99+0.35 =0.63×(100+1) =6.35×(12.5-2.5)
=0.35×(99+1) =0.63×100+0.63×1 =6.35×10
=0.35×100 =63+0.63 =63.5
=35 =63.63
考点综合练习
2.选择题
①在估算5.65×4.38时,与实际结果最接近的是( )。
A.5×4 B.6×4 C.5×5 D.6×6
②已知a>0,下面的算式中得数最大的是( )。
A.a×0.5 B.a÷0.5 C.a×1.5 D.a÷1.5
③ 某手机专卖店以2000元的价格卖出两部不同的手机,一部手机赚了20%,另一部手机亏了20%,对于这两部手机,这个店家( )
A.赚了 B.亏了 C. 不亏也不赚 D.无法确定
B
B
B
考点综合练习
3.解决问题
把一块长米的布条剪成相同长度的10块,共用了3分钟。
①每段布条长多少米?
②剪一次需要多少分钟?
考点综合练习
4.解决问题
学校对四年级的同学观看电视节目的情况调查统计情况如下:
(1)观看《探索发现》的有多少人?
(2)观看《绿色空间》的有多少人?
(3)观看《科技之光》的有多少人?
考点综合练习
5.解决问题
暑假开学前,小明去商店采购学习用品,已知一个书包58.5元,一支钢笔17元,1个文具盒34.8元。买两个书包的钱可以买几只钢笔?
58.5×2=117(元)
117÷17=6(只)······15(元)
答:买两个书包的钱可以买6只钢笔。
考点综合练习
6.脱式计算
484÷(32+12)×9 (26.4+45)÷1.4
=484÷44×9 =71.4÷1.4
=11×9 =51
=99
59.2÷(82-45)×25 42×7.6+42×2.4
=59.2÷37×25 =319.2+100.8
=1.6×25 =420
=40
乘风破浪会有时
直挂云帆济沧海
专题06:数与代数——数的运算
期末专项考点复习
人教版·六年级下册
2023-2024学年
1.整数、小数、分数四则计算的意义。
2.整数、小数、分数四则计算的运算法则。
3.加法、乘法运算定律。
4.应用整数、小数、分数的四则计算知识
解决实际问题。
数的运算
意义
运算定律
解决实际问题
运算法则
单元知识框架
www.islide.cc考点目录CONTENT四则运算的意义四则运算法则运算定律四则混合运算的顺序考点01考点02考点03考点04考点05四则运算的意义
/01
知识梳理
1.整数加法:
(把两个数合并成一个数)的运算叫做加法。在加。法里,相加的数叫做加数,加得的数叫做和。加数是部分数,和是总数。
2.整数减法:
已知(两个加数的和与其中的一个加数),求(另一个加数)的运算叫做减法。被减数是总数,减数和差分别是部分数。加法和减法互为逆运算。
被减数-减数=差
被减数=(差+减数)
减数=(被减数-差)
知识梳理
3.整数乘法:
求(几个相同加数的和)的简便运算叫做乘法。在乘法里,相同的加数和相同加数的个数都叫做因数。相同加数的和叫做积。在乘法里,0和任何数相乘都得0。1和任何数相乘都得任何数。
一个因数×一个因数 =积。
一个因数=(积÷另一个因数)。
4. 整数除法:
已知(两个因数的积与其中一个因数),求(另一个因数的运算)叫做除法。在除法里,已知的积叫做被除数,已知的一个因数叫做除数,所求的因数叫做商。乘法和除法互为逆运算。在除法里,0不能做除数。因为0和任何数相乘都得0,所以任何一个数除以0,均得不到一个确定的商。
被除数÷除数=商
除数=(被除数÷商)
被除数=(商×除数) 。
典型例题
1.下列各算式中,“4”和“5”不能直接相加的算式是( )
A. ①② B. ②③ C.①③ D ②④
A
跟踪练习
学校举行广播体操表演,每行有12人,一共有14行。聪聪通过竖式计算知道一共有168人参加表演(如图)。竖式中箭头所指的可以用下图( )框中的点来表示。
C
四则运算法则
/02
知识梳理
1.整数加法:
把两个数合并成一个数的运算叫做加法。
在加法里,相加的数叫做加数,加得的数叫做和。加数是部分数,和是总数。
关系:加数+加数=和
一个加数=和-另一个加数
2.整数减法:
已知两个加数的和与其中的一个加数,求另一个加数的运算叫做减法。
在减法里,已知的和叫做被减数,已知的加数叫做减数,未知的加数叫做差。被减数是总数,减数和差分别是部分数。
关系:被减数-减数=差
差+减数=被减数
注:加法和减法互为逆运算。
知识梳理
3.整数乘法:
求几个相同加数的和的简便运算叫做乘法。
在乘法里,相同的加数和相同加数的个数都叫做因数。相同加数的和叫做积。
关系:
一个因数× 一个因数 =积
一个因数=积÷另一个因数
注:在乘法里,0和任何数相乘都得0;1和任何数相乘都的任何数。
4.整数除法:
已知两个因数的积与其中一个因数,求另一个因数的运算叫做除法。
在除法里,已知的积叫做被除数,已知的一个因数叫做除数,所求的因数叫做商。
关系:
被除数÷除数=商 除数=被除数÷商 被除数=商×除数
注:乘法和除法互为逆运算。
在除法里,0不能做除数。(因为0和任何数相乘都得0,所以任何一个数除以0,均得不到一个确定的商。)
知识梳理
小数加法:
小数加法的意义与整数加法的意义相同。是把两个数合并成一个数的运算。
小数减法:
小数减法的意义与整数减法的意义相同。已知两个加数的和与其中的一个加数,求另一个加数的运算.
小数乘法:
小数乘整数的意义和整数乘法的意义相同,就是求几个相同加数和的简便运算;一个数乘纯小数的意义是求这个数的十分之几、百分之几、千分之几……是多少。
小数除法:
小数除法的意义与整数除法的意义相同,就是已知两个因数的积与其中一个因数,求另一个因数的运算。
知识梳理
分数加法:
分数加法的意义与整数加法的意义相同。是把两个数合并成一个数的运算。
分数减法:
分数减法的意义与整数减法的意义相同。已知两个加数的和与其中的一个加数,求另一个加数的运算。
分数乘法:
分数乘法的意义与整数乘法的意义相同,就是求几个相同加数和的简便运算。
分数除法:
分数除法的意义与整数除法的意义相同。就是已知两个因数的积与其中一个因数,求另一个因数的运算。
典型例题
脱式计算
460-(24+480÷60 ) 750+360÷15×22
(56-32)÷1.5+198 100÷2.5+120 ÷0.6
=460-(24+8)
=460-32
=428
=750+24×22
=750+528
=1278
=24÷1.5+198
=16+198
=214
=40+200
=240
方法提示:
①同级运算,从左向右依次计算。
②如果既有乘除又有加减,先算乘除,再算加减。
③如果有括号,先算括号里面的,再算括号外面的。
跟踪练习
已知算式75x18=1350,在括号里填上合适的数。
750x1.8=( )
135÷7.5 =( )
1.35÷0.18=( )
( )x( )=1350
( )x( )=1350
1800
18
7.5
7500
0.18
0.75
1350
运算定律
/03
知识梳理
1.加法交换律:
两个数相加,交换加数的位置,它们的和不变,即a+b=b+a 。
2.加法结合律:
三个数相加,先把前两个数相加,再加上第三个数;或者先把后两个数相加,再和第一个数相加它们的和不变,即(a+b)+c=a+(b+c) 。
3.乘法交换律:
两个数相乘,交换因数的位置它们的积不变,即a×b=b×a。
4.乘法结合律:
三个数相乘,先把前两个数相乘,再乘以第三个数;或者先把后两个数相乘,再和第一个数相乘,它们的积不变,即(a×b)×c=a×(b×c) 。
5.乘法分配律:
两个数的和与一个数相乘,可以把两个加数分别与这个数相乘再把两个积相加,即(a+b)×c=a×c+b×c 。
典型例题
【例】用简便方法计算。
【解析】这道题应该仔细观察, 有一个因数 ,而 ,也有一个因数 ,后面的25%等于 ,因此利用乘法分配律计算比较简便。
【解答】
跟踪练习
【解答】
运算的顺序
/04
知识梳理
1. 没有括号的混合运算:
同级运算从(左)往(右)依次运算;两级运算先算(乘、除)法,后算(加减)法。
2. 有括号的混合运算:
先算(小括号里面的),再算(中括号里面的),最后算(括号外面的)。
3. 第一级运算:
(加法和减法)叫做第一级运算。第二级运算:(乘法和除法)叫做第二级运算。
4.小数四则运算的运算顺序:
和整数四则运算顺序相同。
5.分数四则运算的运算顺序:
和整数四则运算顺序相同。
典型例题
【解析】本题考查两级运算及含有括号的四则混合运算。
题中既有中括号又有小括号,先算小括号和中括号里面的,再算括号外面的。在计算时不要急于将小数和分数统一,先观察整个算式的结构特征,再根据需要进行转换,灵活运用。
跟踪练习
计算下面各题。
(1)832-36×24÷27 (2)
【解答】
(1)832-36×24÷27
=832-864÷27
=832-32
=800
考点综合练习
1.用简便方法计算。
3.5×9.9+0.35 0.63×101 6.35×12.5-6.35×2.5
=0.35×99+0.35 =0.63×(100+1) =6.35×(12.5-2.5)
=0.35×(99+1) =0.63×100+0.63×1 =6.35×10
=0.35×100 =63+0.63 =63.5
=35 =63.63
考点综合练习
2.选择题
①在估算5.65×4.38时,与实际结果最接近的是( )。
A.5×4 B.6×4 C.5×5 D.6×6
②已知a>0,下面的算式中得数最大的是( )。
A.a×0.5 B.a÷0.5 C.a×1.5 D.a÷1.5
③ 某手机专卖店以2000元的价格卖出两部不同的手机,一部手机赚了20%,另一部手机亏了20%,对于这两部手机,这个店家( )
A.赚了 B.亏了 C. 不亏也不赚 D.无法确定
B
B
B
考点综合练习
3.解决问题
把一块长米的布条剪成相同长度的10块,共用了3分钟。
①每段布条长多少米?
②剪一次需要多少分钟?
考点综合练习
4.解决问题
学校对四年级的同学观看电视节目的情况调查统计情况如下:
(1)观看《探索发现》的有多少人?
(2)观看《绿色空间》的有多少人?
(3)观看《科技之光》的有多少人?
考点综合练习
5.解决问题
暑假开学前,小明去商店采购学习用品,已知一个书包58.5元,一支钢笔17元,1个文具盒34.8元。买两个书包的钱可以买几只钢笔?
58.5×2=117(元)
117÷17=6(只)······15(元)
答:买两个书包的钱可以买6只钢笔。
考点综合练习
6.脱式计算
484÷(32+12)×9 (26.4+45)÷1.4
=484÷44×9 =71.4÷1.4
=11×9 =51
=99
59.2÷(82-45)×25 42×7.6+42×2.4
=59.2÷37×25 =319.2+100.8
=1.6×25 =420
=40
乘风破浪会有时
直挂云帆济沧海
