专题六:数与代数《式与方程》复习课件(共29张PPT)六年级数学下学期期末核心考点集训(人教版)
文档属性
| 名称 | 专题六:数与代数《式与方程》复习课件(共29张PPT)六年级数学下学期期末核心考点集训(人教版) |  | |
| 格式 | pptx | ||
| 文件大小 | 4.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-25 15:54:16 | ||
图片预览





文档简介
(共29张PPT)
专题06:数与代数——式与方程
期末专项考点复习
人教版·六年级下册
2023-2024学年
单元知识框架
式与方程
等式与方程
列方程解决实际问题
用字母表示数
www.islide.cc考点目录CONTENT用字母表示数等式与方程列方程解决实际问题考点01考点02考点03考点04考点05用字母表示数
/01
知识梳理
用字母代表数:
(1)表示一个具体数量。例如:小红的年龄为a岁。
(2)表示数量关系。例如:路程÷时间=速度,s÷t=v。
(3)表示运算律。例如:乘法分配律,(a+b)xc=axc+bxc。
(4)表示计算公式。例如:三角形面积公式,S=ah÷2。
求值
(1)含有字母的式子不仅可以表示数量关系,也可以表示数量,只要知道给出式子中每个字母的值是多少,就可以算出这个式子表示的数值是多少。
(2)我们计算一个图形的面积或周长时,实际上是把数值代人有关的公式,算出结果就是它的面积或周长。
跟踪练习
·省略乘号后,数必须写在字母的前面。
·数与字母、字母和字母相乘时,乘号可以简写成“·”
或省略不写。
·数与数相乘时,乘号不能省略或写成“·”的形式。
加号、减号、除号都不能省略。
用字母表示数时,有哪些注意事项?
跟踪练习
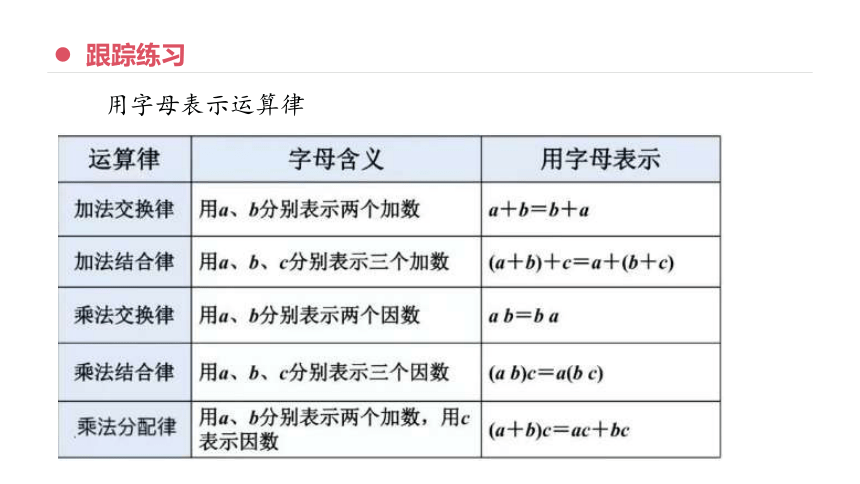
用字母表示运算律
典型例题
1.用含有字母的式子表示下面的数量。
(1)一只青蛙每天吃a只害虫,100天吃掉( )只害虫。
(2)小明今年b岁,再过十年是( )岁。
(3)一堆货物x吨,运走24吨,还剩( )吨。
(4)水果店有x千克苹果,一共装6箱,平均每箱装( )千克。
注意:
①在含有字母的式子里,数和字母中间的乘号可以写作“·”,也可以省略不写。
②省略乘号时,应当把数写在字母的前面。
③数与数之间的乘号不能省略。加号、减号、除号都不能省略。
100a
b+10
x-24
x:6
跟踪练习
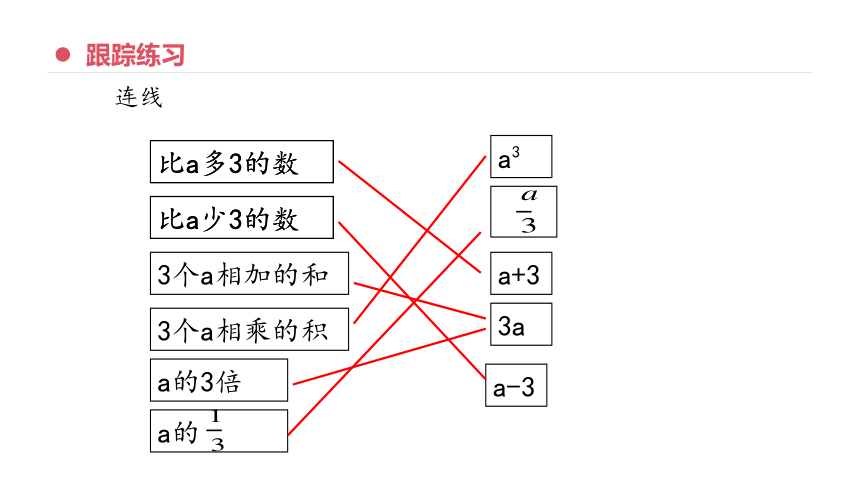
连线
比a多3的数
比a少3的数
3个a相加的和
3个a相乘的积
a的3倍
a的
a+3
a-3
3a
a3
比a多3的数
比a少3的数
等式与方程
/02
知识梳理
等式与方程
(1)等式的意义:表示相等关系的式子叫作等式。
(2)方程的意义:含有未知数的等式叫方程。
(3)等式与方程的关系:方程一定是等式,等式不一定是方程,
知识梳理
等式的性质1: 等式两边同时(加上)或(减去)同一个数,左右两边仍然相等 8十2=10
8+2+5=10+5→15=15
8+2-6=10-6→4=4
等式的性质2: 等式两边同时(乘)同一个数或(除以)同一个不为0的数,左右两边仍然相等 a=20
aX5=20x5→5a=100
a÷2=20÷2→a÷2=102
等式的性质
知识梳理
(1)方程的解的意义:
使方程左右两边相等的未知数的值,叫作方程的解。
(2)解方程的意义:
求方程的解的过程叫作解方程。
(3)解方程的依据:
等式的基本性质(等式的左右两边同时加上或减去同一个数,等式的左右两边仍然相等;等式的左右两边同时乘或除以一个不为0的数,等式的左右两边仍然相等)。
方程的解和解方程
知识梳理
方程的解 使(方程 )左右两边相等的(未知数)的值叫作方程的解。方程的解是一个(数值)
解方程 求方程的解的( 过程)叫作解方程。解方程是一个过程
方程的解和解方程
典型例题
解方程,并检验。
3x-0.4×5=4
解: 3x-2=4
3x-2+2=4+2
3x=6
3x÷3=6÷3
x=2
检验:把x=2代入方程
方程的左边=3x-0.4×5
=3×2-0.4×5
=4
=方程的右边
所以,x=2是方程的解。
跟踪练习
4+ 0.7x = 102
解:
看作整体
老师心中的数乘0.7,再加上4,得到102。你能猜出我心中的这个数吗?
猜数游戏
解:设老师心中的数是x
列方程解决实际问题
/03
知识梳理
一般分5步:
(1)根据题意,解设未知数为x。
(2)找出具体的数量,列出等量关系式。
(3)根据等量关系式,列出方程。
(4)解方程。
(5)检验并答句
列方程解应用题的步骤:
知识梳理
找等量关系是列方程解决实际问题的关键,找等量关系可以通过以下几种方法:
①从题目的关键句中找;
②)从常见的等量关系中找;
③根据图形的周长、面积和体积计算公式找等量关系;
④从题目的叙述顺序中找;
⑤借助线段图找。
知识梳理
用方程解实际问题与用算术法解实际问题的区别:
用方程解实际问题
用算术法解实际问题
1.未知量用字母x表示,参与列式; 2.根据题意找出数量之间的相等关系,列出含有未知数x的等式 1.未知量不参与列式;
2.根据题目中已知数量和未知量之间的关系,确定解答步骤,然后列式计算
典型例题
箱子里装有同样数量的乒乓球和羽毛球。每次取出5个乒乓球和3个羽毛球,取了几次以后,乒乓球没有了,羽毛球还剩6个。一共取了几次?原来乒乓球和羽毛球各有多少个?
解:设一共取了x次。
3 x+6 =5 x
5x-3x =6
2x=6
x=3
羽毛球、乒乓球:5×3=15 (个)
答:……。
跟踪练习
少年宫合唱队有84人,合唱队的人数比舞蹈队的3倍多15人。舞蹈队有多少人?
舞蹈队人数:
合唱队人数:
X
3X
多15人
84人
想:舞蹈队人数×3倍+15=合唱队的人数
解:设舞蹈队有X人。
3X +15=84
3X=84-15
3X=69
X=23
答:舞蹈队有23人。
考点综合练习
1.学校买来9个足球,每个ɑ元,又买来b个篮球,每个58元。
9ɑ表示
58 b表示
58-ɑ表示
9ɑ+ 58b表示
如果ɑ=45,b = 6则9ɑ+58b=
9个足球的总价
b个篮球的总价
篮球的单价比足球的单价贵多少钱
学校买足球和篮球的总价钱
9×45+58×6=753
考点综合练习
先算的部分能直接计算的,先计算。
先算的部分含有x而不能算,把这部分当成一个数。
几个地方有末知数的,先合并同类项。
括号里有末知数,先算但不能算,把括号看成一个数。
考点综合练习
3.用含有字母的式子表示下面的数量
(1)一只青蛙每天吃a只害虫,100天吃掉( )只害虫。
(2)小明今年b岁,再过十年是( )岁。
(3)一堆货物 x 吨,运走24吨,还剩( )吨。
(4) m 表示一个偶数,与他相邻的两个偶数是( )和( )。
(5)等腰三角形的顶角是n度,一个底角是( )度。
100a
b+10
X-24
m-2
m+2
(180-n) ÷2
考点综合练习
解:设小云踢了x下。
x=84
答:小云踢了84下。
4.
小芳在踢毽子比赛中踢了63个,她踢毽子的数量是小云的 。小云踢了多少个?(用方程解决问题。)
x=63
考点综合练习
5.
用一根绳子测井深,将绳4折,井外还余8尺;将绳6折,正好等于井深,绳长几尺?井深几尺?
解:设井深x尺,则绳长6x尺。
6x=4x+8
2x=8
x=4
答:绳长24尺,井深4尺。
6x=24
考点综合练习
如左图,一个正方形的边长增加它的 后,得到的新正方形的周长是48cm,原正方形的边长是多少厘米?
6.
解:设原正方形的边长是x厘米。
x=9
答:原正方形的边长是9厘米。
乘风破浪会有时
直挂云帆济沧海
专题06:数与代数——式与方程
期末专项考点复习
人教版·六年级下册
2023-2024学年
单元知识框架
式与方程
等式与方程
列方程解决实际问题
用字母表示数
www.islide.cc考点目录CONTENT用字母表示数等式与方程列方程解决实际问题考点01考点02考点03考点04考点05用字母表示数
/01
知识梳理
用字母代表数:
(1)表示一个具体数量。例如:小红的年龄为a岁。
(2)表示数量关系。例如:路程÷时间=速度,s÷t=v。
(3)表示运算律。例如:乘法分配律,(a+b)xc=axc+bxc。
(4)表示计算公式。例如:三角形面积公式,S=ah÷2。
求值
(1)含有字母的式子不仅可以表示数量关系,也可以表示数量,只要知道给出式子中每个字母的值是多少,就可以算出这个式子表示的数值是多少。
(2)我们计算一个图形的面积或周长时,实际上是把数值代人有关的公式,算出结果就是它的面积或周长。
跟踪练习
·省略乘号后,数必须写在字母的前面。
·数与字母、字母和字母相乘时,乘号可以简写成“·”
或省略不写。
·数与数相乘时,乘号不能省略或写成“·”的形式。
加号、减号、除号都不能省略。
用字母表示数时,有哪些注意事项?
跟踪练习
用字母表示运算律
典型例题
1.用含有字母的式子表示下面的数量。
(1)一只青蛙每天吃a只害虫,100天吃掉( )只害虫。
(2)小明今年b岁,再过十年是( )岁。
(3)一堆货物x吨,运走24吨,还剩( )吨。
(4)水果店有x千克苹果,一共装6箱,平均每箱装( )千克。
注意:
①在含有字母的式子里,数和字母中间的乘号可以写作“·”,也可以省略不写。
②省略乘号时,应当把数写在字母的前面。
③数与数之间的乘号不能省略。加号、减号、除号都不能省略。
100a
b+10
x-24
x:6
跟踪练习
连线
比a多3的数
比a少3的数
3个a相加的和
3个a相乘的积
a的3倍
a的
a+3
a-3
3a
a3
比a多3的数
比a少3的数
等式与方程
/02
知识梳理
等式与方程
(1)等式的意义:表示相等关系的式子叫作等式。
(2)方程的意义:含有未知数的等式叫方程。
(3)等式与方程的关系:方程一定是等式,等式不一定是方程,
知识梳理
等式的性质1: 等式两边同时(加上)或(减去)同一个数,左右两边仍然相等 8十2=10
8+2+5=10+5→15=15
8+2-6=10-6→4=4
等式的性质2: 等式两边同时(乘)同一个数或(除以)同一个不为0的数,左右两边仍然相等 a=20
aX5=20x5→5a=100
a÷2=20÷2→a÷2=102
等式的性质
知识梳理
(1)方程的解的意义:
使方程左右两边相等的未知数的值,叫作方程的解。
(2)解方程的意义:
求方程的解的过程叫作解方程。
(3)解方程的依据:
等式的基本性质(等式的左右两边同时加上或减去同一个数,等式的左右两边仍然相等;等式的左右两边同时乘或除以一个不为0的数,等式的左右两边仍然相等)。
方程的解和解方程
知识梳理
方程的解 使(方程 )左右两边相等的(未知数)的值叫作方程的解。方程的解是一个(数值)
解方程 求方程的解的( 过程)叫作解方程。解方程是一个过程
方程的解和解方程
典型例题
解方程,并检验。
3x-0.4×5=4
解: 3x-2=4
3x-2+2=4+2
3x=6
3x÷3=6÷3
x=2
检验:把x=2代入方程
方程的左边=3x-0.4×5
=3×2-0.4×5
=4
=方程的右边
所以,x=2是方程的解。
跟踪练习
4+ 0.7x = 102
解:
看作整体
老师心中的数乘0.7,再加上4,得到102。你能猜出我心中的这个数吗?
猜数游戏
解:设老师心中的数是x
列方程解决实际问题
/03
知识梳理
一般分5步:
(1)根据题意,解设未知数为x。
(2)找出具体的数量,列出等量关系式。
(3)根据等量关系式,列出方程。
(4)解方程。
(5)检验并答句
列方程解应用题的步骤:
知识梳理
找等量关系是列方程解决实际问题的关键,找等量关系可以通过以下几种方法:
①从题目的关键句中找;
②)从常见的等量关系中找;
③根据图形的周长、面积和体积计算公式找等量关系;
④从题目的叙述顺序中找;
⑤借助线段图找。
知识梳理
用方程解实际问题与用算术法解实际问题的区别:
用方程解实际问题
用算术法解实际问题
1.未知量用字母x表示,参与列式; 2.根据题意找出数量之间的相等关系,列出含有未知数x的等式 1.未知量不参与列式;
2.根据题目中已知数量和未知量之间的关系,确定解答步骤,然后列式计算
典型例题
箱子里装有同样数量的乒乓球和羽毛球。每次取出5个乒乓球和3个羽毛球,取了几次以后,乒乓球没有了,羽毛球还剩6个。一共取了几次?原来乒乓球和羽毛球各有多少个?
解:设一共取了x次。
3 x+6 =5 x
5x-3x =6
2x=6
x=3
羽毛球、乒乓球:5×3=15 (个)
答:……。
跟踪练习
少年宫合唱队有84人,合唱队的人数比舞蹈队的3倍多15人。舞蹈队有多少人?
舞蹈队人数:
合唱队人数:
X
3X
多15人
84人
想:舞蹈队人数×3倍+15=合唱队的人数
解:设舞蹈队有X人。
3X +15=84
3X=84-15
3X=69
X=23
答:舞蹈队有23人。
考点综合练习
1.学校买来9个足球,每个ɑ元,又买来b个篮球,每个58元。
9ɑ表示
58 b表示
58-ɑ表示
9ɑ+ 58b表示
如果ɑ=45,b = 6则9ɑ+58b=
9个足球的总价
b个篮球的总价
篮球的单价比足球的单价贵多少钱
学校买足球和篮球的总价钱
9×45+58×6=753
考点综合练习
先算的部分能直接计算的,先计算。
先算的部分含有x而不能算,把这部分当成一个数。
几个地方有末知数的,先合并同类项。
括号里有末知数,先算但不能算,把括号看成一个数。
考点综合练习
3.用含有字母的式子表示下面的数量
(1)一只青蛙每天吃a只害虫,100天吃掉( )只害虫。
(2)小明今年b岁,再过十年是( )岁。
(3)一堆货物 x 吨,运走24吨,还剩( )吨。
(4) m 表示一个偶数,与他相邻的两个偶数是( )和( )。
(5)等腰三角形的顶角是n度,一个底角是( )度。
100a
b+10
X-24
m-2
m+2
(180-n) ÷2
考点综合练习
解:设小云踢了x下。
x=84
答:小云踢了84下。
4.
小芳在踢毽子比赛中踢了63个,她踢毽子的数量是小云的 。小云踢了多少个?(用方程解决问题。)
x=63
考点综合练习
5.
用一根绳子测井深,将绳4折,井外还余8尺;将绳6折,正好等于井深,绳长几尺?井深几尺?
解:设井深x尺,则绳长6x尺。
6x=4x+8
2x=8
x=4
答:绳长24尺,井深4尺。
6x=24
考点综合练习
如左图,一个正方形的边长增加它的 后,得到的新正方形的周长是48cm,原正方形的边长是多少厘米?
6.
解:设原正方形的边长是x厘米。
x=9
答:原正方形的边长是9厘米。
乘风破浪会有时
直挂云帆济沧海
