19.2.9 一次函数与二元一次方程组(第三课时) 课件(共29张PPT)
文档属性
| 名称 | 19.2.9 一次函数与二元一次方程组(第三课时) 课件(共29张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 5.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-26 21:46:22 | ||
图片预览






文档简介
(共29张PPT)
人教八下数学
同步优质课件
人教版八年级下册
复习回顾
学习目标
知识精讲
典例解析
针对练习
总结提升
达标检测
小结梳理
2024春人教版八(下)数学同步精品课件
19.2 一次函数
19.2.9 一次函数与二元一次方程组
第十九章 一次函数
1.理解一次函数与二元一次方程(组)的关系;
2.掌握二元一次方程组的解与函数图象的交点坐标的关系.(重点、难点)
x+y=5 它表示什么呢?
它表示一个二元一次方程.
y=-x+5 它表示什么呢?
它既可表示一个二元一次方程,又可表示一个一次函数.
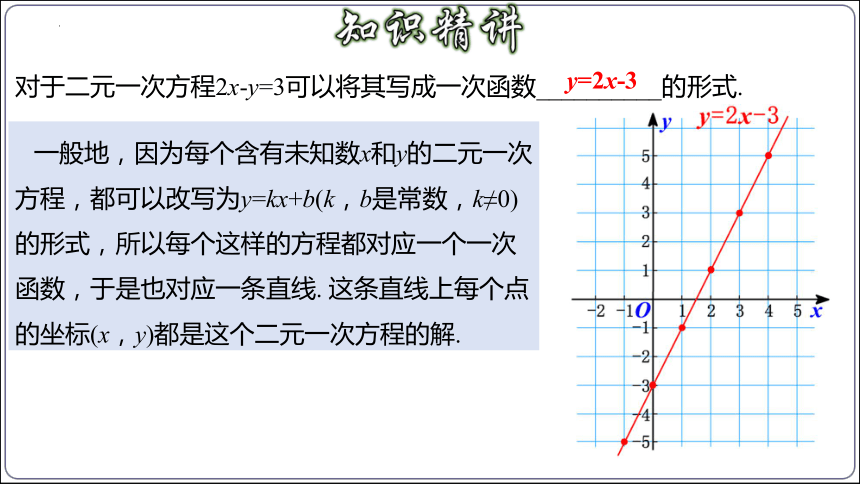
对于二元一次方程2x-y=3可以将其写成一次函数__________的形式.
1.画出一次函数y=2x-3的图象;
2.找出方程的几组解;
3.把以这几组解为坐标的点在坐标系上描出来,你发现了什么?
4.在一次函数y=2x-3的图象上点的坐标都是二元一次方程2x-y=3的解吗?
y=2x-3
一般地,因为每个含有未知数x和y的二元一次方程,都可以改写为y=kx+b(k,b是常数,k≠0)的形式,所以每个这样的方程都对应一个一次函数,于是也对应一条直线. 这条直线上每个点的坐标(x,y)都是这个二元一次方程的解.
对于二元一次方程2x-y=3可以将其写成一次函数__________的形式.
y=2x-3
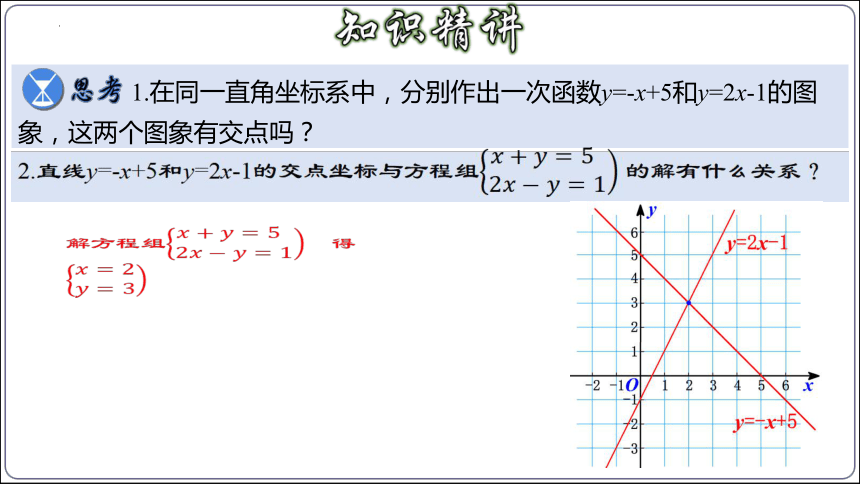
1.在同一直角坐标系中,分别作出一次函数y=-x+5和y=2x-1的图象,这两个图象有交点吗?
2.直线y=-x+5和y=2x-1的交点坐标与方程组 的解有什么关系?
解方程组 得
由含有未知数x和y的两个二元一次方程组成的每个二元一次方程组,都对应两个一次函数,于是也对应两条直线.
从“数”的角度看,解这样的方程组,相当于求自变量为何值时相应的两个函数值相等,以及这个函数值是多少;
从“形”的角度看,解这样的方程组,相当于确定两条相应直线交点的坐标. 因此,我们可以用画一次函数图象的方法得到方程组的解.
例1.1号探测气球从海拔5m处出发,以1m/min的速度上升.与此同时,2号探测气球从海拔15m处出发,以0.5m/min的速度上升.两个气球都上升了1h.
(1)用式子分别表示两个气球所在位置的海拔y(单位:m)关于上升时间x(单位:min)的函数关系;
(2)在某时刻两个气球能否位于同一高度?如果能,这时气球
上升了多长时间?位于什么高度?
解:(1)气球上升时间x满足0≤x≤60.
对于1号气球,y关于x的函数解析式为y=x+5.
对于2号气球,y关于x的函数解析式为y=0.5x+15.
(2)在某时刻两个气球能否位于同一高度?如果能,这时气球上升了多长时间?位于什么高度?
(2)在某时刻两个气球位于同一高度,就是说对于x的某个值(0≤x≤60),函数y=x+5和y=0.5x+15有相同的值y.
由此可得 解得
这就是说,当上升20min时,两个气球都位于海拔25m的高度.
(2)在某时刻两个气球能否位于同一高度?如果能,这时气球上升了多长时间?位于什么高度?
在同一直角坐标系中,画出一次函数
y=x+5和y=0.5x+15的图象.
两条直线交点坐标为(20,25),这也说
明当上升20min时,两个气球都位于海
拔25m的高度.
某公司要印制宣传材料,甲、乙两个印刷厂可选择,甲印刷厂只收取印制费,乙印刷厂收费包括印制费和制版费.
(1)甲印刷厂每份宣传材料的印制费是______元;
(2)求乙印刷厂收费y(元)关于印制数量x(份)的函数表达式,并说明一次项系数,常数项的实际意义;
(3)当两个印刷厂的花费一样多时,求此时的印制数量.
解:(1)由图可得,甲印刷厂每份宣传材料的印制费为:
(元)
某公司要印制宣传材料,甲、乙两个印刷厂可选择,甲印刷厂只收取印制费,乙印刷厂收费包括印制费和制版费.
(2)求乙印刷厂收费y(元)关于印制数量x(份)的函数表达式,并说明一次项系数,常数项的实际意义;
解:(2)设乙印刷厂收费y(元)关于印制数量x(份)的函数表达式为,
由图可得,在图象上,代入,得
,解得:
∴,
一次项系数1代表每份宣传材料的印制费为1元,
常数项1500代表制版费为1500元.
某公司要印制宣传材料,甲、乙两个印刷厂可选择,甲印刷厂只收取印制费,乙印刷厂收费包括印制费和制版费.
(3)当两个印刷厂的花费一样多时,求此时的印制数量.
解:(3)由(1)知甲印刷厂每份宣传材料的印制费
是2.5元,
∴甲印刷厂收费y(元)关于印制数量x(份)的函
数表达式为,
联立两函数解析式得
解得,
∴两函数图象交点坐标为,
当两个印刷厂的花费一样多时,求此时的印制数量为1000份.
例2.如图,直线与直线分别交y轴于点A和点B,且两直线相交于点P.
(1)求交点P的坐标;
(2)若点Q在x轴上,且满足,求点Q的坐标.
解:(1)解方程组
解得:,
∴点P的坐标为:.
例2.如图,直线与直线分别交y轴于点A和点B,且两直线相交于点P.
(1)求交点P的坐标;
(2)若点Q在x轴上,且满足,求点Q的坐标.
(2)把代入得:,
把代入得:,
∴点A的坐标为:,点B的坐标为:,
∴,
设点,
∵,
∴,
解得:,
∴点Q的坐标为或.
1.把二元一次方程3y-2x=12化为y=kx+b的形式为( )
A.y=-x+4 B. y=x-4 C.y=x+4 D.y=-x-4
2.如图所示的图象中,以方程2x-y+2=0的解为坐标的点所组成的图象是( )
C
C
3.一次函数y=3x+6与y=2x-4的图象交于点(-10,-24),则是下列哪个方程组的解( )
A. B. C. D.
4.在同一平面直角坐标系中,若一次函数y=-x+3与y=3x-5的图象交于点M,则点M的坐标为( )
A. (-1,4) B. (-1,2) C. (2,-1) D. (2,1)
C
D
5.若直线y=-x+a与直线y=x+b的交点坐标为(2,8),则a-b的值为( )
A.2 B.4 C.6 D.8
6.用图象法解方程组时,下列选项中的图象正确的是( )
B
C
7.直线l1: y=k1x+b与直线l2: y=k2x在同一平面直角坐标系中的图象如图所示,则关于x、y的方程组的解为________.
8.根据图象信息填空:
(1)方程组的解是_________;
(2)不等式ax+bx<2
9.我们规定:当k,b为常数,k≠0, b≠0, k≠b时,一次函数y=kx+b与y=bx+k互为交换函数,例如: y=4x+3的交换函数为y=3x+4.一次函数y=kx+2与它的交换函数的图象交点的横坐标为______.
1
10.用函数图象求解下列方程.
(1)2x﹣3=x﹣2; (2)x+3=2x+1.
解:(1)画出一次函数y=2x﹣3和y=x﹣2的
图象,如图①所示,
交点坐标为(1,﹣1),
∴方程2x﹣3=x﹣2的解为x=1.
10.用函数图象求解下列方程.
(1)2x﹣3=x﹣2; (2)x+3=2x+1.
(2)画出一次函数y=x+3和y=2x+1的图象,如图②所示,
交点坐标为(2,5),
∴方程x+3=2x+1的解为x=2.
11.考虑下表两种移动电话计费方式
用函数方法解答何时两种计费方式费用相等.
解:用x(min)表示通话时间,y(元)表示费用.则方式一的函数解析式为y=0.15x+20,方式二的函数解析式为y=0.2x.列得方程组
解得
答:当通话时间为400min时,两种计费方式费用相等,都为80元.
12.如图,已知直线y=kx+b经过点B(1,4),且与直线y=-x-11平行,与直线y=2x- 4交于点C,与x轴交于点A. 求直线AB的解析式及点C的坐标.
解:直线y=kx+b与直线y= -x-11平行
∴k=-1
∵直线y=-x+b经过点B(1,4)
∴-1+b=4, 解得b=5
∴直线AB的解析式为y=-x+5
联立方程组,解得
∴点C(3,2)
由含有未知数x和y的两个二元一次方程组成的每个二元一次方程组,都对应两个一次函数,于是也对应两条直线.
从“数”的角度看,解这样的方程组,相当于求自变量为何值时相应的两个函数值相等,以及这个函数值是多少;
从“形”的角度看,解这样的方程组,相当于确定两条相应直线交点的坐标. 因此,我们可以用画一次函数图象的方法得到方程组的解.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
人教八下数学
同步优质课件
人教版八年级下册
复习回顾
学习目标
知识精讲
典例解析
针对练习
总结提升
达标检测
小结梳理
2024春人教版八(下)数学同步精品课件
19.2 一次函数
19.2.9 一次函数与二元一次方程组
第十九章 一次函数
1.理解一次函数与二元一次方程(组)的关系;
2.掌握二元一次方程组的解与函数图象的交点坐标的关系.(重点、难点)
x+y=5 它表示什么呢?
它表示一个二元一次方程.
y=-x+5 它表示什么呢?
它既可表示一个二元一次方程,又可表示一个一次函数.
对于二元一次方程2x-y=3可以将其写成一次函数__________的形式.
1.画出一次函数y=2x-3的图象;
2.找出方程的几组解;
3.把以这几组解为坐标的点在坐标系上描出来,你发现了什么?
4.在一次函数y=2x-3的图象上点的坐标都是二元一次方程2x-y=3的解吗?
y=2x-3
一般地,因为每个含有未知数x和y的二元一次方程,都可以改写为y=kx+b(k,b是常数,k≠0)的形式,所以每个这样的方程都对应一个一次函数,于是也对应一条直线. 这条直线上每个点的坐标(x,y)都是这个二元一次方程的解.
对于二元一次方程2x-y=3可以将其写成一次函数__________的形式.
y=2x-3
1.在同一直角坐标系中,分别作出一次函数y=-x+5和y=2x-1的图象,这两个图象有交点吗?
2.直线y=-x+5和y=2x-1的交点坐标与方程组 的解有什么关系?
解方程组 得
由含有未知数x和y的两个二元一次方程组成的每个二元一次方程组,都对应两个一次函数,于是也对应两条直线.
从“数”的角度看,解这样的方程组,相当于求自变量为何值时相应的两个函数值相等,以及这个函数值是多少;
从“形”的角度看,解这样的方程组,相当于确定两条相应直线交点的坐标. 因此,我们可以用画一次函数图象的方法得到方程组的解.
例1.1号探测气球从海拔5m处出发,以1m/min的速度上升.与此同时,2号探测气球从海拔15m处出发,以0.5m/min的速度上升.两个气球都上升了1h.
(1)用式子分别表示两个气球所在位置的海拔y(单位:m)关于上升时间x(单位:min)的函数关系;
(2)在某时刻两个气球能否位于同一高度?如果能,这时气球
上升了多长时间?位于什么高度?
解:(1)气球上升时间x满足0≤x≤60.
对于1号气球,y关于x的函数解析式为y=x+5.
对于2号气球,y关于x的函数解析式为y=0.5x+15.
(2)在某时刻两个气球能否位于同一高度?如果能,这时气球上升了多长时间?位于什么高度?
(2)在某时刻两个气球位于同一高度,就是说对于x的某个值(0≤x≤60),函数y=x+5和y=0.5x+15有相同的值y.
由此可得 解得
这就是说,当上升20min时,两个气球都位于海拔25m的高度.
(2)在某时刻两个气球能否位于同一高度?如果能,这时气球上升了多长时间?位于什么高度?
在同一直角坐标系中,画出一次函数
y=x+5和y=0.5x+15的图象.
两条直线交点坐标为(20,25),这也说
明当上升20min时,两个气球都位于海
拔25m的高度.
某公司要印制宣传材料,甲、乙两个印刷厂可选择,甲印刷厂只收取印制费,乙印刷厂收费包括印制费和制版费.
(1)甲印刷厂每份宣传材料的印制费是______元;
(2)求乙印刷厂收费y(元)关于印制数量x(份)的函数表达式,并说明一次项系数,常数项的实际意义;
(3)当两个印刷厂的花费一样多时,求此时的印制数量.
解:(1)由图可得,甲印刷厂每份宣传材料的印制费为:
(元)
某公司要印制宣传材料,甲、乙两个印刷厂可选择,甲印刷厂只收取印制费,乙印刷厂收费包括印制费和制版费.
(2)求乙印刷厂收费y(元)关于印制数量x(份)的函数表达式,并说明一次项系数,常数项的实际意义;
解:(2)设乙印刷厂收费y(元)关于印制数量x(份)的函数表达式为,
由图可得,在图象上,代入,得
,解得:
∴,
一次项系数1代表每份宣传材料的印制费为1元,
常数项1500代表制版费为1500元.
某公司要印制宣传材料,甲、乙两个印刷厂可选择,甲印刷厂只收取印制费,乙印刷厂收费包括印制费和制版费.
(3)当两个印刷厂的花费一样多时,求此时的印制数量.
解:(3)由(1)知甲印刷厂每份宣传材料的印制费
是2.5元,
∴甲印刷厂收费y(元)关于印制数量x(份)的函
数表达式为,
联立两函数解析式得
解得,
∴两函数图象交点坐标为,
当两个印刷厂的花费一样多时,求此时的印制数量为1000份.
例2.如图,直线与直线分别交y轴于点A和点B,且两直线相交于点P.
(1)求交点P的坐标;
(2)若点Q在x轴上,且满足,求点Q的坐标.
解:(1)解方程组
解得:,
∴点P的坐标为:.
例2.如图,直线与直线分别交y轴于点A和点B,且两直线相交于点P.
(1)求交点P的坐标;
(2)若点Q在x轴上,且满足,求点Q的坐标.
(2)把代入得:,
把代入得:,
∴点A的坐标为:,点B的坐标为:,
∴,
设点,
∵,
∴,
解得:,
∴点Q的坐标为或.
1.把二元一次方程3y-2x=12化为y=kx+b的形式为( )
A.y=-x+4 B. y=x-4 C.y=x+4 D.y=-x-4
2.如图所示的图象中,以方程2x-y+2=0的解为坐标的点所组成的图象是( )
C
C
3.一次函数y=3x+6与y=2x-4的图象交于点(-10,-24),则是下列哪个方程组的解( )
A. B. C. D.
4.在同一平面直角坐标系中,若一次函数y=-x+3与y=3x-5的图象交于点M,则点M的坐标为( )
A. (-1,4) B. (-1,2) C. (2,-1) D. (2,1)
C
D
5.若直线y=-x+a与直线y=x+b的交点坐标为(2,8),则a-b的值为( )
A.2 B.4 C.6 D.8
6.用图象法解方程组时,下列选项中的图象正确的是( )
B
C
7.直线l1: y=k1x+b与直线l2: y=k2x在同一平面直角坐标系中的图象如图所示,则关于x、y的方程组的解为________.
8.根据图象信息填空:
(1)方程组的解是_________;
(2)不等式ax+b
9.我们规定:当k,b为常数,k≠0, b≠0, k≠b时,一次函数y=kx+b与y=bx+k互为交换函数,例如: y=4x+3的交换函数为y=3x+4.一次函数y=kx+2与它的交换函数的图象交点的横坐标为______.
1
10.用函数图象求解下列方程.
(1)2x﹣3=x﹣2; (2)x+3=2x+1.
解:(1)画出一次函数y=2x﹣3和y=x﹣2的
图象,如图①所示,
交点坐标为(1,﹣1),
∴方程2x﹣3=x﹣2的解为x=1.
10.用函数图象求解下列方程.
(1)2x﹣3=x﹣2; (2)x+3=2x+1.
(2)画出一次函数y=x+3和y=2x+1的图象,如图②所示,
交点坐标为(2,5),
∴方程x+3=2x+1的解为x=2.
11.考虑下表两种移动电话计费方式
用函数方法解答何时两种计费方式费用相等.
解:用x(min)表示通话时间,y(元)表示费用.则方式一的函数解析式为y=0.15x+20,方式二的函数解析式为y=0.2x.列得方程组
解得
答:当通话时间为400min时,两种计费方式费用相等,都为80元.
12.如图,已知直线y=kx+b经过点B(1,4),且与直线y=-x-11平行,与直线y=2x- 4交于点C,与x轴交于点A. 求直线AB的解析式及点C的坐标.
解:直线y=kx+b与直线y= -x-11平行
∴k=-1
∵直线y=-x+b经过点B(1,4)
∴-1+b=4, 解得b=5
∴直线AB的解析式为y=-x+5
联立方程组,解得
∴点C(3,2)
由含有未知数x和y的两个二元一次方程组成的每个二元一次方程组,都对应两个一次函数,于是也对应两条直线.
从“数”的角度看,解这样的方程组,相当于求自变量为何值时相应的两个函数值相等,以及这个函数值是多少;
从“形”的角度看,解这样的方程组,相当于确定两条相应直线交点的坐标. 因此,我们可以用画一次函数图象的方法得到方程组的解.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
