19.3 课题学习 选择方案课件(共38张PPT)
文档属性
| 名称 | 19.3 课题学习 选择方案课件(共38张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-26 21:47:14 | ||
图片预览




文档简介
(共38张PPT)
人教八下数学
同步优质课件
人教版八年级下册
复习回顾
学习目标
知识精讲
典例解析
针对练习
总结提升
达标检测
小结梳理
2024春人教版八(下)数学同步精品课件
19.3 课题学习 选择方案
第十九章 一次函数
1.会用一次函数知识解决方案选择问题,体会函数模型思想;(重点、难点)
2.能从不同的角度思考问题,优化解决问题的方法;
3.能进行解决问题过程的反思,总结解决问题的方法.
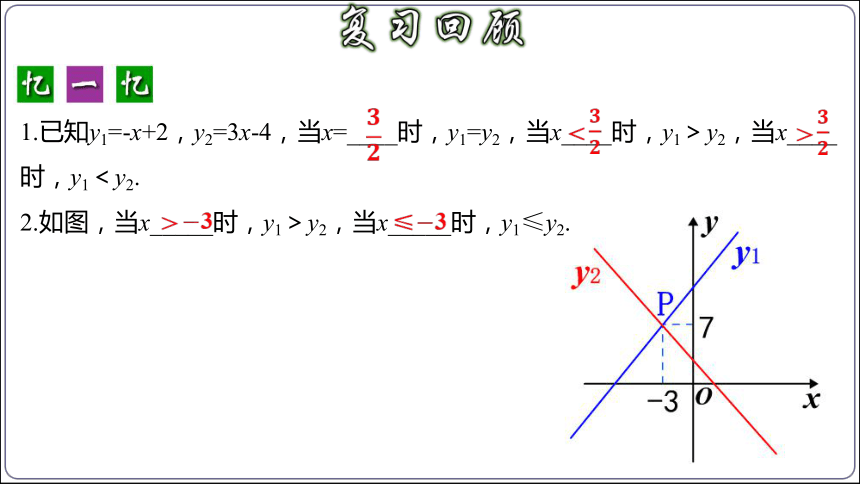
1.已知y1=-x+2,y2=3x-4,当x=____时,y1=y2,当x____时,y1>y2,当x____时,y1<y2.
2.如图,当x_____时,y1>y2,当x_____时,y1≤y2.
<
>
>3
≤3
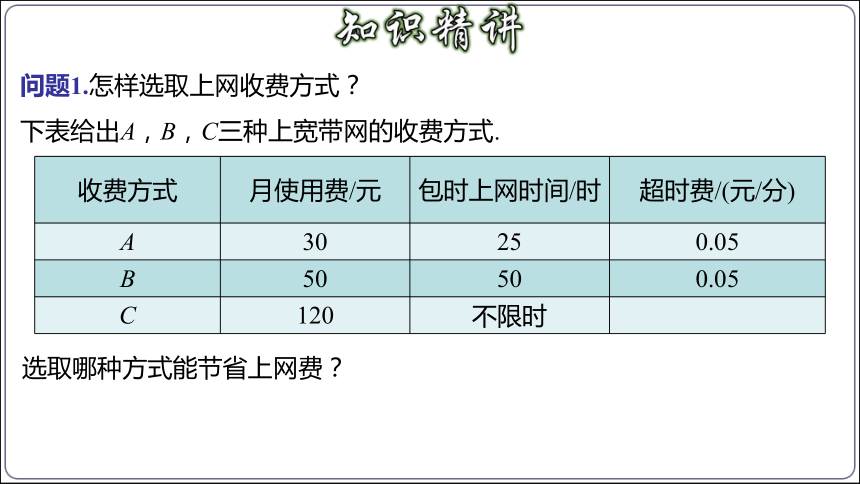
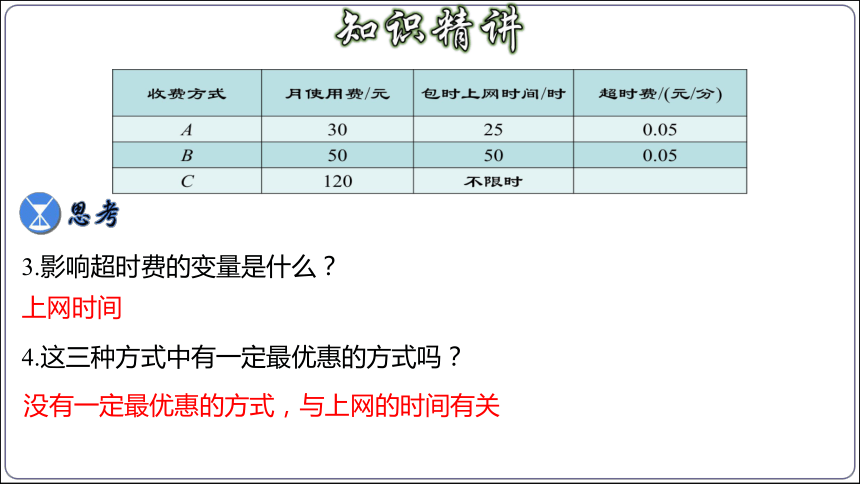
问题1.怎样选取上网收费方式?
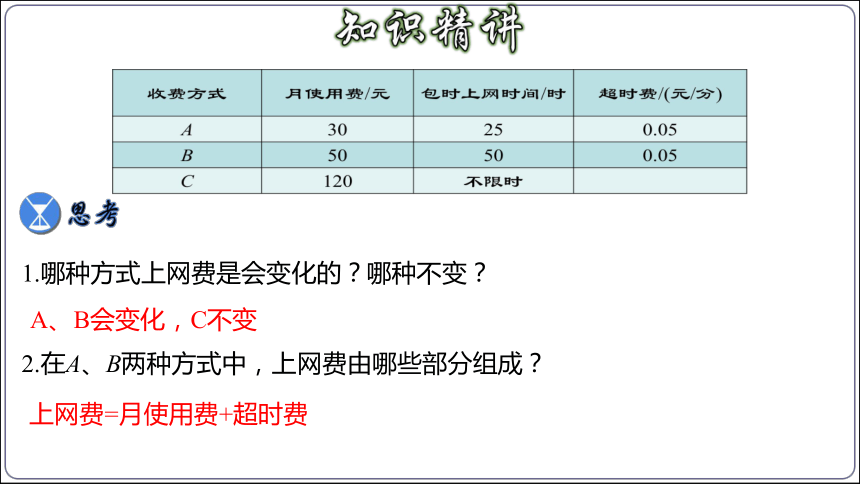
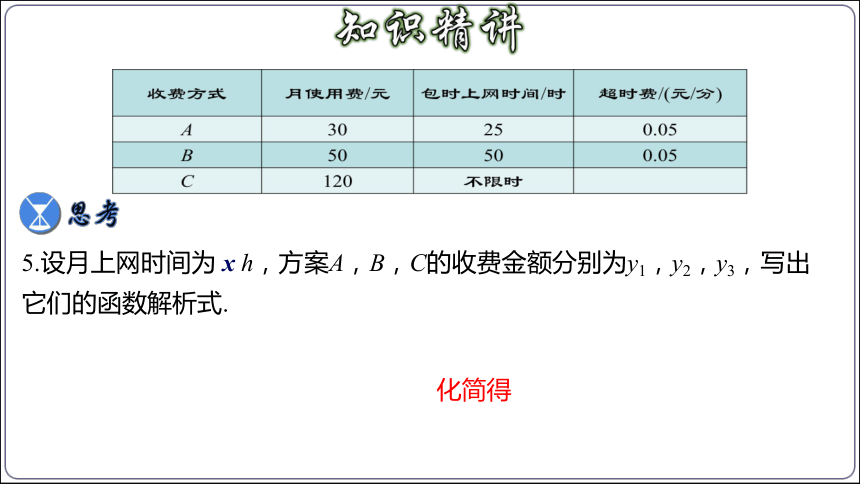
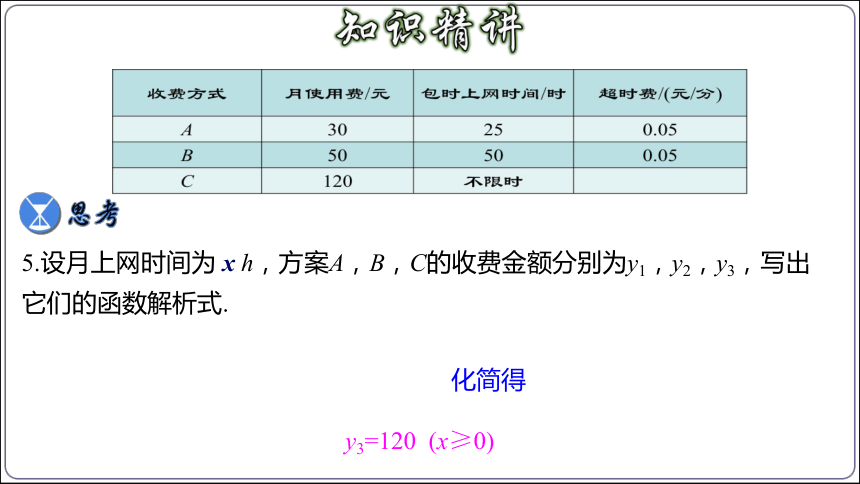
下表给出A,B,C三种上宽带网的收费方式.
收费方式 月使用费/元 包时上网时间/时 超时费/(元/分)
A 30 25 0.05
B 50 50 0.05
C 120 不限时
选取哪种方式能节省上网费?
1.哪种方式上网费是会变化的?哪种不变?
2.在A、B两种方式中,上网费由哪些部分组成?
A、B会变化,C不变
上网费=月使用费+超时费
3.影响超时费的变量是什么?
4.这三种方式中有一定最优惠的方式吗?
上网时间
没有一定最优惠的方式,与上网的时间有关
5.设月上网时间为 x h,方案A,B,C的收费金额分别为y1,y2,y3,写出它们的函数解析式.
化简得
5.设月上网时间为 x h,方案A,B,C的收费金额分别为y1,y2,y3,写出它们的函数解析式.
化简得
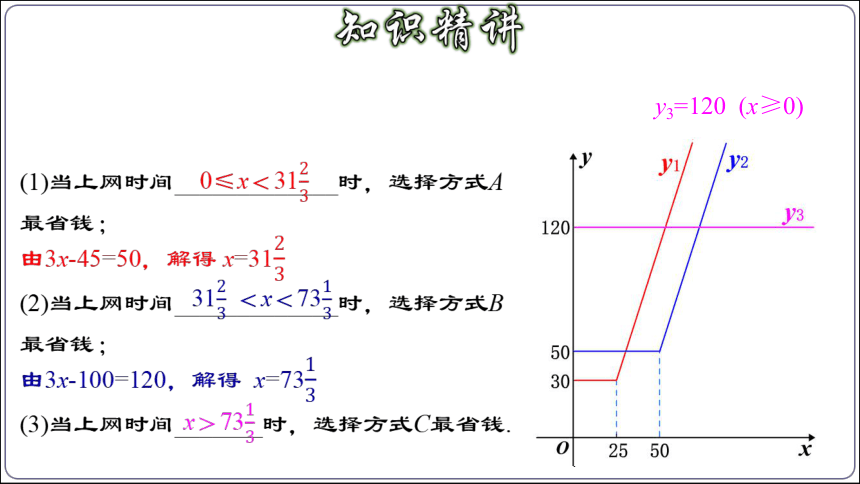
y3=120 (x≥0)
y3=120 (x≥0)
(1)当上网时间_____________时,选择方式A最省钱;
由3x-45=50,解得 x=31
(2)当上网时间_____________时,选择方式B最省钱;
由3x-100=120,解得 x=73
(3)当上网时间_______时,选择方式C最省钱.
0≤x<31
31<x<73
x>73
问题2. 怎样租车?
某学校计划在总费用2300元限额内,租用汽车送234名学生和6名教师集体外出活动,每辆汽车上至少要有1名教师.现有甲、乙两种大客车,它们的载客量和租金如下表所示.
甲种客车 乙种客车
载客量(单位:人/辆) 45 30
租金 (单位:元/辆) 400 280
(1)共需租多少辆汽车?
(2)给出最节省费用的租车方案.
甲种客车 乙种客车
载客量(单位:人/辆) 45 30
租金 (单位:元/辆) 400 280
总费用2300元
送234名学生
6名教师
(1)共需租多少辆汽车?
解:(1)要保证240名师生都有车坐,汽车总数不能小于6辆;
要使每辆汽上至少要有1名教师,汽车总数不能大于6辆.
综合起来可知汽车总数为6辆.
甲种客车 乙种客车
载客量(单位:人/辆) 45 30
租金 (单位:元/辆) 400 280
总费用2300元
送234名学生
6名教师
(2)给出最节省费用的租车方案.
解:设租用x辆甲种客车,则租车费用y(单位:元)是x的函数,即
y=400x+280(6-x)
化简为:y=120x+1680
由
解得 4≤x≤5 ,
∴ y=120x+1680 (4≤x≤5 )
甲种客车 乙种客车
载客量(单位:人/辆) 45 30
租金 (单位:元/辆) 400 280
总费用2300元
送234名学生
6名教师
(2)给出最节省费用的租车方案.
方案一:当x=4时,即租用4辆甲种汽车,2辆乙种汽车. 租车费用y=120×4+1680=2160(元)
方案二:当x=5时,即租用5辆甲种汽车,1辆乙种汽车. 租车费用y=120×5+1680=2280(元)
因此,为节省费用应选择方案一.
还有其它选择方案的方法吗?
甲种客车 乙种客车
载客量(单位:人/辆) 45 30
租金 (单位:元/辆) 400 280
总费用2300元
送234名学生
6名教师
(2)给出最节省费用的租车方案.
由k=120>0 可知,函数值y随x增大而增大.
∴当x=4时,y最小=120×4+1680=2160
即租用4辆甲种汽车,2辆乙种汽车时,租车费用最省为2160元.
y=120x+1680 (4≤x≤5 )
型号 A B
成本(万元/台) 200 240
售价(万元/台) 250 300
(1)该厂对这两种型号挖掘机有几种生产方案?
(2)该厂如何生产获得最大利润?
(3)根据市场调查,每台B型挖掘机的售价不会改变,每台A型挖掘机的售价将会提高m万元(m>0),该厂如何生产可以获得最大利润?(注:利润=售价-成本)
例1.某工程机械厂根据市场要求,计划生产A、B两种型号的大型挖掘机共100台,该厂所筹生产资金不少于22400万元,但不超过22500万元,且所筹资金全部用于生产这两种型号的挖掘机,所生产的这两种型号的挖掘机可全部售出,此两种型号挖掘机的生产成本和售价如下表所示:
解:(1)设生产A型挖掘机x台,则B型挖掘机可生产(100-x)台,由题意知:
(1)该厂对这两种型号挖掘机有几种生产方案?
分析:设生产A型挖掘机x台,则B型挖掘机可生产(100-x)台,由题意得不等式组 ;
∴有三种生产方案:A型38台,B型62台;A型39台,B型61台;A型40台,
B型60台.
解得 37.5≤x≤40
∵x取正整数, ∴x为38、39、40
∴当x=38时,W最大=5620(万元),
即生产A型38台,B型62台时,获得利润最大.
(2)该厂如何生产获得最大利润?
分析:利润与两种挖掘机的数量有关,因此可建立利润与挖掘机数量的函数关系式;
W=50x+60(100-x)
= -10x+6000
解:设获得利润为W(万元),由题意知:
(3)根据市场调查,每台B型挖掘机的售价不会改变,每台A型挖掘机的售价将会提高m万元(m>0),该厂如何生产可以获得最大利润?
③当m>10时,取x=40,W最大,即A型挖掘机生产40台,B型生产60台.
分析:在(2)的基础上,售价改变,则应重新建立利润与挖掘机数量的函数关系式,并注意讨论m的取值范围.
解:由题意知:W=(50+m)x+60(100-x)
= (m-10)x+6000
∴①当0<m<10时,取x=38,W最大 ,即A型挖掘机生产38台,B型挖掘机生产62台;
②当m=10时,m-10=0,三种生产获得利润相等;
例2.抗旱救灾行动中,江津、白沙两地要向中山和广兴每天输送饮用水,其中江津每天输出60车饮用水,白沙每天输出40车饮用水,供给中山和广兴各50车饮用水.由于距离不同,江津到中山需600元/车,到广兴需700元/车;白沙到中山需500元/车,到广兴需650元/车.请你设计一个调运方案使总运费最低?此时总运费为多少元?
广兴
50车
中山
50车
江津
60车
白沙
40车
例2.抗旱救灾行动中,江津、白沙两地要向中山和广兴每天输送饮用水,其中江津每天输出60车饮用水,白沙每天输出40车饮用水,供给中山和广兴各50车饮用水.由于距离不同,江津到中山需600元/车,到广兴需700元/车;白沙到中山需500元/车,到广兴需650元/车.请你设计一个调运方案使总运费最低?此时总运费为多少元?
中山 广兴
江津 x
白沙
解:设每天要从江津运x车到中山
(60-x)
(50-x)
(x-10)
解:设每天要从江津运x车到中山,总运费为y元.由题意可得
y=600x+700(60-x)+500(50-x)+650(x-10)
整理得 y=50x+60500
中山 广兴
江津 x
白沙
(60-x)
(50-x)
(x-10)
由
得
∴
∴ y=50x+60500(10≤x≤50)
∵ k=50>0 ,y随x的增大而增大,
∴当x=10时,y有最小值,y=61000.
答:从江津调往中山10车,从江津调往广兴50车,从白沙调往中山40车,从白沙调往广兴0车,可使总费用最省,为61000元.
中山 广兴
江津 x
白沙
(60-x)
(50-x)
(x-10)
1.某单位需要用车,准备和一个体车主或一国有出租车公司其中的一家签订合同.设汽车每月行驶xkm,应付给个体车主的月租费是y1元,付给出租车公司的月租费是y2元,y1,y2分别与x之间的函数关系图象是如下图的两条直线.观察图象,回答下列问题:
(1)每月行驶的路程等于_____km时,租两家出
租车的费用相同;
(2)每月行驶的路程x_______时,y1租个体车主
的出租车合算;
(3)如果这个单位估计每月行驶的路程为1300km,
那么这个单位租______________的出租车合算.
1500
>1500
国有出租车公司
2.某校实行学案式教学,需印制若干份数学学案.印刷厂有甲、乙两种收费方式,除按份数收取印刷费外,甲种方式还需收取制版费而乙种不需要.两种印刷方式的费用y(元)与印刷份数x(份)之间的函数关系如图所示:
(1)填空:甲种收费方式的解析式为_____________,
乙种收费方式的函数解析式为___________;
(2)该校某年级每次需印制100~450 (含100和450)份
学案,选择哪种印制方式较合算
y=0.1x+6
y=0.12x
(1)填空:甲种收费方式的解析式为_____________,
乙种收费方式的函数解析式为___________;
(2)该校某年级每次需印制100~450 (含100和450)份
学案,选择哪种印制方式较合算
y=0.1x+6
y=0.12x
解: (2)由0.1x+6>0.12x,得x<300,由0.1x+6=0.12x,得x=300,由0.1x+6<0.12x,得x>300.
由此可知:当100≤x<300时,选择乙种方式较合算;当x=300时,选择甲乙两种方式都一样;当3003.某商场筹集资金12.8万元,一次性购进空调、彩电共30台.根据市场需要,这些空调、彩电可以全部销售,全部销售后利润不少于1.5万元,其中空调、彩电的进价和售价见表格.
设商场计划购进空调x台,空调空调彩电和彩电全部销售后商场获得的进价为y元.
(1)试写出y与x的函数关系式;
(2)商场有哪几种进货方案可供选择
(3)选择哪种方案,商场获利最大 最大利润是多少元
解: (1) y= (6100-5400)x+ (3900-3500) (30-x)
化简,得y=300x+12000
3.某商场筹集资金12.8万元,一次性购进空调、彩电共30台.根据市场需要,这些空调、彩电可以全部销售,全部销售后利润不少于1.5万元,其中空调、彩电的进价和售价见表格.
设商场计划购进空调x台,空调空调彩电和彩电全部销售后商场获得的进价为y元.
(1)试写出y与x的函数关系式;
(2)商场有哪几种进货方案可供选择
(3)选择哪种方案,商场获利最大 最大利润是多少元
解: (2) 10≤x≤12
(2)商场有哪几种进货方案可供选择
解: (2) 10≤x≤12
∵x为整数
∴x=10或11或12
∴商场有以下三种方案可供选择:
方案1:购空调10台,购彩电20台;
方案2:购空调11台,购彩电19台;
方案3:购空调12台,购彩电18台.
(3)选择哪种方案,商场获利最大 最大利润是多少元
解: (3)∵y=300x+12000 (10≤x≤12)
其中k=300>0. y随x的增大而增大
∴当x=12时,y有最大值,y最大=300×12+12000=15600元.
故选择方案3:购空调12台,购彩电18台时,商场获利最大,最大利润是15600元.
4.某游泳馆每年夏季推出两种游泳付费方式,方式一:先购买会员证,每张会员证200元,只限本人当年使用,凭证游泳每次再付费10元;方式二:不购买会员证,每次游泳付费18元.设小明计划今年夏季游泳次数为x(x为正整数).
(1)根据题意,填写下表:
(2)若小明计划今年夏季游泳的总费用为540元,则选择哪种付费方式,他游泳的次数比较多
解:(2)方式一:令200+10x=540,解得x=34
方式二:令18x=540,解得x=30
∵34>30,
∴选择方式一付费,他游泳的次数比较多.
(3)当x>20时,小明选择哪种付费方式更合算 请说明理由.
解: (3) 令200+10x<18x,得x>25
令200+10x=18x,得x=25
令200+10x>18x,得x<25
∴当20当x=25时,小明选择两种付费方式一样;
当x>25时,小明选择方式一付费合算.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
人教八下数学
同步优质课件
人教版八年级下册
复习回顾
学习目标
知识精讲
典例解析
针对练习
总结提升
达标检测
小结梳理
2024春人教版八(下)数学同步精品课件
19.3 课题学习 选择方案
第十九章 一次函数
1.会用一次函数知识解决方案选择问题,体会函数模型思想;(重点、难点)
2.能从不同的角度思考问题,优化解决问题的方法;
3.能进行解决问题过程的反思,总结解决问题的方法.
1.已知y1=-x+2,y2=3x-4,当x=____时,y1=y2,当x____时,y1>y2,当x____时,y1<y2.
2.如图,当x_____时,y1>y2,当x_____时,y1≤y2.
<
>
>3
≤3
问题1.怎样选取上网收费方式?
下表给出A,B,C三种上宽带网的收费方式.
收费方式 月使用费/元 包时上网时间/时 超时费/(元/分)
A 30 25 0.05
B 50 50 0.05
C 120 不限时
选取哪种方式能节省上网费?
1.哪种方式上网费是会变化的?哪种不变?
2.在A、B两种方式中,上网费由哪些部分组成?
A、B会变化,C不变
上网费=月使用费+超时费
3.影响超时费的变量是什么?
4.这三种方式中有一定最优惠的方式吗?
上网时间
没有一定最优惠的方式,与上网的时间有关
5.设月上网时间为 x h,方案A,B,C的收费金额分别为y1,y2,y3,写出它们的函数解析式.
化简得
5.设月上网时间为 x h,方案A,B,C的收费金额分别为y1,y2,y3,写出它们的函数解析式.
化简得
y3=120 (x≥0)
y3=120 (x≥0)
(1)当上网时间_____________时,选择方式A最省钱;
由3x-45=50,解得 x=31
(2)当上网时间_____________时,选择方式B最省钱;
由3x-100=120,解得 x=73
(3)当上网时间_______时,选择方式C最省钱.
0≤x<31
31<x<73
x>73
问题2. 怎样租车?
某学校计划在总费用2300元限额内,租用汽车送234名学生和6名教师集体外出活动,每辆汽车上至少要有1名教师.现有甲、乙两种大客车,它们的载客量和租金如下表所示.
甲种客车 乙种客车
载客量(单位:人/辆) 45 30
租金 (单位:元/辆) 400 280
(1)共需租多少辆汽车?
(2)给出最节省费用的租车方案.
甲种客车 乙种客车
载客量(单位:人/辆) 45 30
租金 (单位:元/辆) 400 280
总费用2300元
送234名学生
6名教师
(1)共需租多少辆汽车?
解:(1)要保证240名师生都有车坐,汽车总数不能小于6辆;
要使每辆汽上至少要有1名教师,汽车总数不能大于6辆.
综合起来可知汽车总数为6辆.
甲种客车 乙种客车
载客量(单位:人/辆) 45 30
租金 (单位:元/辆) 400 280
总费用2300元
送234名学生
6名教师
(2)给出最节省费用的租车方案.
解:设租用x辆甲种客车,则租车费用y(单位:元)是x的函数,即
y=400x+280(6-x)
化简为:y=120x+1680
由
解得 4≤x≤5 ,
∴ y=120x+1680 (4≤x≤5 )
甲种客车 乙种客车
载客量(单位:人/辆) 45 30
租金 (单位:元/辆) 400 280
总费用2300元
送234名学生
6名教师
(2)给出最节省费用的租车方案.
方案一:当x=4时,即租用4辆甲种汽车,2辆乙种汽车. 租车费用y=120×4+1680=2160(元)
方案二:当x=5时,即租用5辆甲种汽车,1辆乙种汽车. 租车费用y=120×5+1680=2280(元)
因此,为节省费用应选择方案一.
还有其它选择方案的方法吗?
甲种客车 乙种客车
载客量(单位:人/辆) 45 30
租金 (单位:元/辆) 400 280
总费用2300元
送234名学生
6名教师
(2)给出最节省费用的租车方案.
由k=120>0 可知,函数值y随x增大而增大.
∴当x=4时,y最小=120×4+1680=2160
即租用4辆甲种汽车,2辆乙种汽车时,租车费用最省为2160元.
y=120x+1680 (4≤x≤5 )
型号 A B
成本(万元/台) 200 240
售价(万元/台) 250 300
(1)该厂对这两种型号挖掘机有几种生产方案?
(2)该厂如何生产获得最大利润?
(3)根据市场调查,每台B型挖掘机的售价不会改变,每台A型挖掘机的售价将会提高m万元(m>0),该厂如何生产可以获得最大利润?(注:利润=售价-成本)
例1.某工程机械厂根据市场要求,计划生产A、B两种型号的大型挖掘机共100台,该厂所筹生产资金不少于22400万元,但不超过22500万元,且所筹资金全部用于生产这两种型号的挖掘机,所生产的这两种型号的挖掘机可全部售出,此两种型号挖掘机的生产成本和售价如下表所示:
解:(1)设生产A型挖掘机x台,则B型挖掘机可生产(100-x)台,由题意知:
(1)该厂对这两种型号挖掘机有几种生产方案?
分析:设生产A型挖掘机x台,则B型挖掘机可生产(100-x)台,由题意得不等式组 ;
∴有三种生产方案:A型38台,B型62台;A型39台,B型61台;A型40台,
B型60台.
解得 37.5≤x≤40
∵x取正整数, ∴x为38、39、40
∴当x=38时,W最大=5620(万元),
即生产A型38台,B型62台时,获得利润最大.
(2)该厂如何生产获得最大利润?
分析:利润与两种挖掘机的数量有关,因此可建立利润与挖掘机数量的函数关系式;
W=50x+60(100-x)
= -10x+6000
解:设获得利润为W(万元),由题意知:
(3)根据市场调查,每台B型挖掘机的售价不会改变,每台A型挖掘机的售价将会提高m万元(m>0),该厂如何生产可以获得最大利润?
③当m>10时,取x=40,W最大,即A型挖掘机生产40台,B型生产60台.
分析:在(2)的基础上,售价改变,则应重新建立利润与挖掘机数量的函数关系式,并注意讨论m的取值范围.
解:由题意知:W=(50+m)x+60(100-x)
= (m-10)x+6000
∴①当0<m<10时,取x=38,W最大 ,即A型挖掘机生产38台,B型挖掘机生产62台;
②当m=10时,m-10=0,三种生产获得利润相等;
例2.抗旱救灾行动中,江津、白沙两地要向中山和广兴每天输送饮用水,其中江津每天输出60车饮用水,白沙每天输出40车饮用水,供给中山和广兴各50车饮用水.由于距离不同,江津到中山需600元/车,到广兴需700元/车;白沙到中山需500元/车,到广兴需650元/车.请你设计一个调运方案使总运费最低?此时总运费为多少元?
广兴
50车
中山
50车
江津
60车
白沙
40车
例2.抗旱救灾行动中,江津、白沙两地要向中山和广兴每天输送饮用水,其中江津每天输出60车饮用水,白沙每天输出40车饮用水,供给中山和广兴各50车饮用水.由于距离不同,江津到中山需600元/车,到广兴需700元/车;白沙到中山需500元/车,到广兴需650元/车.请你设计一个调运方案使总运费最低?此时总运费为多少元?
中山 广兴
江津 x
白沙
解:设每天要从江津运x车到中山
(60-x)
(50-x)
(x-10)
解:设每天要从江津运x车到中山,总运费为y元.由题意可得
y=600x+700(60-x)+500(50-x)+650(x-10)
整理得 y=50x+60500
中山 广兴
江津 x
白沙
(60-x)
(50-x)
(x-10)
由
得
∴
∴ y=50x+60500(10≤x≤50)
∵ k=50>0 ,y随x的增大而增大,
∴当x=10时,y有最小值,y=61000.
答:从江津调往中山10车,从江津调往广兴50车,从白沙调往中山40车,从白沙调往广兴0车,可使总费用最省,为61000元.
中山 广兴
江津 x
白沙
(60-x)
(50-x)
(x-10)
1.某单位需要用车,准备和一个体车主或一国有出租车公司其中的一家签订合同.设汽车每月行驶xkm,应付给个体车主的月租费是y1元,付给出租车公司的月租费是y2元,y1,y2分别与x之间的函数关系图象是如下图的两条直线.观察图象,回答下列问题:
(1)每月行驶的路程等于_____km时,租两家出
租车的费用相同;
(2)每月行驶的路程x_______时,y1租个体车主
的出租车合算;
(3)如果这个单位估计每月行驶的路程为1300km,
那么这个单位租______________的出租车合算.
1500
>1500
国有出租车公司
2.某校实行学案式教学,需印制若干份数学学案.印刷厂有甲、乙两种收费方式,除按份数收取印刷费外,甲种方式还需收取制版费而乙种不需要.两种印刷方式的费用y(元)与印刷份数x(份)之间的函数关系如图所示:
(1)填空:甲种收费方式的解析式为_____________,
乙种收费方式的函数解析式为___________;
(2)该校某年级每次需印制100~450 (含100和450)份
学案,选择哪种印制方式较合算
y=0.1x+6
y=0.12x
(1)填空:甲种收费方式的解析式为_____________,
乙种收费方式的函数解析式为___________;
(2)该校某年级每次需印制100~450 (含100和450)份
学案,选择哪种印制方式较合算
y=0.1x+6
y=0.12x
解: (2)由0.1x+6>0.12x,得x<300,由0.1x+6=0.12x,得x=300,由0.1x+6<0.12x,得x>300.
由此可知:当100≤x<300时,选择乙种方式较合算;当x=300时,选择甲乙两种方式都一样;当300
设商场计划购进空调x台,空调空调彩电和彩电全部销售后商场获得的进价为y元.
(1)试写出y与x的函数关系式;
(2)商场有哪几种进货方案可供选择
(3)选择哪种方案,商场获利最大 最大利润是多少元
解: (1) y= (6100-5400)x+ (3900-3500) (30-x)
化简,得y=300x+12000
3.某商场筹集资金12.8万元,一次性购进空调、彩电共30台.根据市场需要,这些空调、彩电可以全部销售,全部销售后利润不少于1.5万元,其中空调、彩电的进价和售价见表格.
设商场计划购进空调x台,空调空调彩电和彩电全部销售后商场获得的进价为y元.
(1)试写出y与x的函数关系式;
(2)商场有哪几种进货方案可供选择
(3)选择哪种方案,商场获利最大 最大利润是多少元
解: (2) 10≤x≤12
(2)商场有哪几种进货方案可供选择
解: (2) 10≤x≤12
∵x为整数
∴x=10或11或12
∴商场有以下三种方案可供选择:
方案1:购空调10台,购彩电20台;
方案2:购空调11台,购彩电19台;
方案3:购空调12台,购彩电18台.
(3)选择哪种方案,商场获利最大 最大利润是多少元
解: (3)∵y=300x+12000 (10≤x≤12)
其中k=300>0. y随x的增大而增大
∴当x=12时,y有最大值,y最大=300×12+12000=15600元.
故选择方案3:购空调12台,购彩电18台时,商场获利最大,最大利润是15600元.
4.某游泳馆每年夏季推出两种游泳付费方式,方式一:先购买会员证,每张会员证200元,只限本人当年使用,凭证游泳每次再付费10元;方式二:不购买会员证,每次游泳付费18元.设小明计划今年夏季游泳次数为x(x为正整数).
(1)根据题意,填写下表:
(2)若小明计划今年夏季游泳的总费用为540元,则选择哪种付费方式,他游泳的次数比较多
解:(2)方式一:令200+10x=540,解得x=34
方式二:令18x=540,解得x=30
∵34>30,
∴选择方式一付费,他游泳的次数比较多.
(3)当x>20时,小明选择哪种付费方式更合算 请说明理由.
解: (3) 令200+10x<18x,得x>25
令200+10x=18x,得x=25
令200+10x>18x,得x<25
∴当20
当x>25时,小明选择方式一付费合算.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
