20.2.2 数据的波动程度(第二课时)【2024春人教八下数学同步优质课件】(共32张PPT)
文档属性
| 名称 | 20.2.2 数据的波动程度(第二课时)【2024春人教八下数学同步优质课件】(共32张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 4.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-27 10:26:35 | ||
图片预览









文档简介
(共32张PPT)
人教八下数学
同步优质课件
人教版八年级下册
复习回顾
学习目标
知识精讲
典例解析
针对练习
总结提升
达标检测
小结梳理
2024春人教版八(下)数学同步精品课件
20.2 数据的波动程度
20.2.2 数据的波动程度(2)
第二十章 数据的分析
1.能熟练计算一组数据的方差; (重点)
2.能用样本的方差估计总体的方差及根据方差做决策.(难点)
学习目标
s2= [(x1- )2+(x2 - )2+ +(xn - )2]
计算方差的步骤可概括为“先平均,后求差,平方后,再平均”.
方差的计算公式:
方差越大,数据的波动越大;
方差越小,数据的波动越小.
方差的适用条件:
当两组数据的平均数相等或相近时,才利用方差来判断它们的波动情况.
1.某一段时间,小芳测得连续五天的日最高气温后,整理得出下表(有两个数据被遮盖):
被遮盖的两个数据依次是( )
A.3℃,2 B.3℃,4 C.4℃,2 D.4℃,4
D
2.甲、乙两台包装机同时分装质量为400g的奶粉,从它们各自分装的奶粉中随机抽取了10袋,测得它们的实际质量(单位:g)如下:
甲:401 395 408 404 410 406 400 393 392 391
乙:403 404 397 395 402 401 403 395 402 398
哪台包装机包装的奶粉质量比较稳定?
解:甲、乙两台包装机包装的奶粉平均质量分别是
甲:401 395 408 404 410 406 400 393 392 391
乙:403 404 397 395 402 401 403 395 402 398
哪台包装机包装的奶粉质量比较稳定?
它们的方差分别是
由 > 可知,乙包装机包装的奶粉质量比较稳定.
例1.某快餐公司的香辣鸡腿很受消费者欢迎.现有甲、乙两家农副产品加工厂到快餐公司推销鸡腿,两家鸡腿的价格相同,品质相近,快餐公司决定通过检查鸡腿的质量来确定选购哪
家的鸡腿.检查人员从两家的鸡腿中各随机抽取15个,记录它们的质量如下(单位:g)如下
表.根据表中的数据,你认为快餐公司应选购哪家工厂的鸡腿.
解:检查人员从甲、乙两家农副产品加工厂各随机抽取的15个鸡腿分别组成一个样本,样本数据的平均数分别是
样本数据的方差分别是
由 可知,两家加工厂的鸡腿质量大致相等;由 < 可知,甲加工厂的鸡腿质量更稳定,大小更均匀. 因此,快餐公司应该选购甲加工厂生产的鸡腿.
某跳远队准备从甲、乙两名运动员中选取成绩稳定的一名参加比赛.下表是这两名运动员10次测验成绩(单位:m).
你认为应该选择哪名运动员参赛?为什么?
解:甲、乙两名运动员的平均成绩分别是
它们的方差分别是
由 可知,甲、乙两名运动员的平均成绩大至相等;由 < 可知,甲的成绩更稳定.
如果要从中选出一人参加市级比赛,历届比赛表明,成绩达到5.92m就能夺冠,你认为应选谁参加比赛?如果历届比赛成绩表明,成绩达到6.08m就能打破记录,你认为又应该选谁参加这次比赛呢?
解:甲成绩更稳定,如果成绩达到5.92m就能夺冠,应选甲参赛;乙达到6.08m的可能性较大,如果成绩达到6.08m能打破纪录,应选乙参赛.
例2.在某旅游景区上山的一条小路上,有一些断断续续高低不等的台阶.如图是其中的甲、乙两段台阶路的示意图(图中数字表示每一阶的高度,单位:cm).哪段台阶路走起来更舒服?为什么?
21
20
21
19
19
20
甲
17
24
20
17
19
23
乙
分析:通过计算两段台阶的方差,比较波动性大小.
∴走甲台阶的波动性更,走起来更舒适.
解:
∵
例3.某校要从甲、乙两名跳远运动员中挑选一人参加一项校际比赛.在最近10次选拔赛中,他们的成绩(单位: cm)如下:
甲:585 596 610 598 612 597 604 600 613 601
乙:613 618 580 574 618 593 585 590 598 624
(1)这两名运动员的运动成绩各有何特点?
【分析】分别计算出平均数和方差;根据平均数判断出谁的成绩好,根据方差判断出谁的成绩波动大.
解:
(585+596+610+598+612+597+604+600+613+601)
=601.6,s2甲≈65.84;
(613+618+580+574+618+593+585+590+598+624)
=599.3,s2乙≈284.21.
由上面计算结果可知:甲队员的平均成绩较好,也比较稳定,乙队员的成绩相对不稳定.但甲队员的成绩不突出,乙队员和甲队员相比比较突出.
(2)历届比赛表明,成绩达到5.96m就很可能夺冠,你认为为了夺冠应选谁参加这项比赛?如果历届比赛成绩表明,成绩达到6.10m就能打破纪录,那么你认为为了打破纪录应选谁参加这项比赛.
解:从平均数分析可知,甲、乙两队员都有夺冠的可能.但由方差分析可知,甲成绩比较平稳,夺冠的可能性比乙大.
但要打破纪录,成绩要比较突出,因此乙队员打破纪录的可能性大,我认为为了打破纪录,应选乙队员参加这项比赛.
1.“恒盛”超市购进一批大米,大米的标准包装为每袋30kg,售货员任选6袋进行了称重检验,超过标准重量的记作“﹢”,不足标准重量的记作“﹣”,他记录的结果是+0.5,-0. 5,0,-0.5,-0.5,+1,那么这6袋大米重量的平均数和方差分别是( )
A.30,0.4 B.0, C.30, D.30.5,0.4
C
2.四名运动员参加了射击预选赛,他们成绩的平均环数及其方差s2如下表所示,如果选出一个成绩较好且状态稳定的人去参赛,那么应选( )
A.甲 B.乙 C.丙 D.丁
B
3.甲、乙两名同学进行射击训练,在相同条件下各射靶5次,命中环数统计如下:
甲:8,7,8,8,9 乙:9,7,5,10,9
(1)根据以上信息完成下表:
(2)如果乙再射击1次,命中8环,那么乙的射击成绩的方差________(填“变大”“变小”或“不变”).
变小
4.为了从甲、乙两名学生中选择一人参加电脑知识竞赛,在相同条件下对他们的电脑知识进行了10次测验,成绩如下,(单位:分):
(1)请填写下表:
(2)利用以上信息,请从两个不同的角度对甲、乙两名同学的成绩进行分析.
(2)利用以上信息,请从两个不同的角度对甲、乙两名同学的成绩进行分析.
解:甲成绩的众数是84,乙成绩的众数是90,从两人成绩的众数看,乙的成绩较好;甲成绩的方差是14.4,乙成绩的方差是38.4,从成绩的方差看,甲的成绩相对稳定.
5.两台机床同时生产直径是40mm的零件,为了鉴别机床性能好坏,检验产品的质量,从产品抽出10件进行测量(单位:mm),,结果如下表(超过40mm记为“+”,低于40mm记为“-”)所示:
问哪个机床性能更好些
解:样本数据的平均数分别是
它们的方差分别是
由 可知及 > 可知,乙机床的性能更好些.
6.甲、乙两位同学本学年每单元的测验成绩如下(单位:分)
甲:98,100,100,90,91,89, 99, 100, 100, 93
乙:98,99,94,95,92,92,98,96,99, 97
(1)他们的平均成绩分别是多少
(2)甲、乙的10次单元测验成绩的方差分别是多少
(3)这两位同学的成绩各有什么特点
(4)现要从中选出一人参加“希望杯”竞赛,历届比赛成绩表明,平时成绩达到98分以上才可能进入决赛,你认为应选谁参加这项竞赛,为什么
6.甲、乙两位同学本学年每单元的测验成绩如下(单位:分)
甲:98,100,100,90,91,89, 99, 100, 100, 93
乙:98,99,94,95,92,92,98,96,99, 97
(1)他们的平均成绩分别是多少
解: (1) 他们的平均成绩分别是
6.甲、乙两位同学本学年每单元的测验成绩如下(单位:分)
甲:98,100,100,90,91,89, 99, 100, 100, 93
乙:98,99,94,95,92,92,98,96,99, 97
(2)甲、乙的10次单元测验成绩的方差分别是多少
(2)甲、 乙的10次单元测验成绩的方差分别是
6.甲、乙两位同学本学年每单元的测验成绩如下(单位:分)
甲:98,100,100,90,91,89, 99, 100, 100, 93
乙:98,99,94,95,92,92,98,96,99, 97
(3)这两位同学的成绩各有什么特点
(3) 两位同学的平均成绩相同;乙的方差小于甲的方差,故乙的成绩比甲更稳定;甲虽然成绩不稳定,但发挥好时成绩比乙优秀.
6.甲、乙两位同学本学年每单元的测验成绩如下(单位:分)
甲:98,100,100,90,91,89, 99, 100, 100, 93
乙:98,99,94,95,92,92,98,96,99, 97
(4)现要从中选出一人参加“希望杯”竞赛,历届比赛成绩表明,平时成绩达到98分以上才可能进入决赛,你认为应选谁参加这项竞赛,为什么
(4) 选甲去,因为甲的成绩有6次达到98分以上,而乙只有4次.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
人教八下数学
同步优质课件
人教版八年级下册
复习回顾
学习目标
知识精讲
典例解析
针对练习
总结提升
达标检测
小结梳理
2024春人教版八(下)数学同步精品课件
20.2 数据的波动程度
20.2.2 数据的波动程度(2)
第二十章 数据的分析
1.能熟练计算一组数据的方差; (重点)
2.能用样本的方差估计总体的方差及根据方差做决策.(难点)
学习目标
s2= [(x1- )2+(x2 - )2+ +(xn - )2]
计算方差的步骤可概括为“先平均,后求差,平方后,再平均”.
方差的计算公式:
方差越大,数据的波动越大;
方差越小,数据的波动越小.
方差的适用条件:
当两组数据的平均数相等或相近时,才利用方差来判断它们的波动情况.
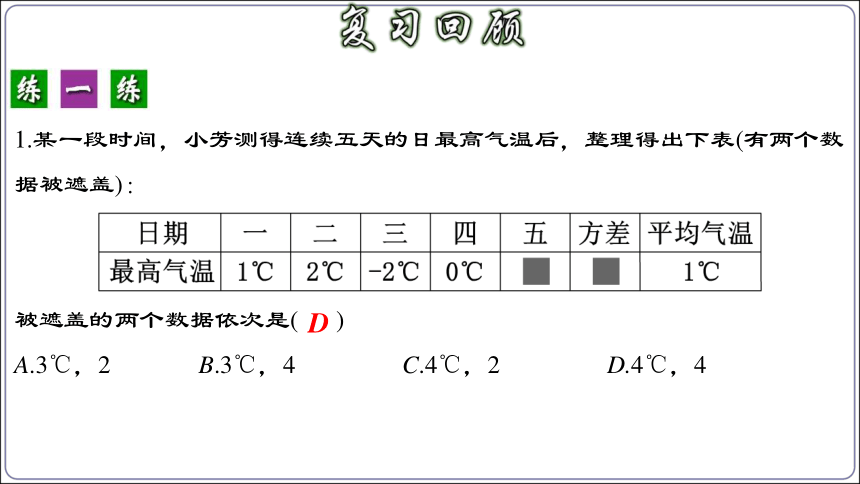
1.某一段时间,小芳测得连续五天的日最高气温后,整理得出下表(有两个数据被遮盖):
被遮盖的两个数据依次是( )
A.3℃,2 B.3℃,4 C.4℃,2 D.4℃,4
D
2.甲、乙两台包装机同时分装质量为400g的奶粉,从它们各自分装的奶粉中随机抽取了10袋,测得它们的实际质量(单位:g)如下:
甲:401 395 408 404 410 406 400 393 392 391
乙:403 404 397 395 402 401 403 395 402 398
哪台包装机包装的奶粉质量比较稳定?
解:甲、乙两台包装机包装的奶粉平均质量分别是
甲:401 395 408 404 410 406 400 393 392 391
乙:403 404 397 395 402 401 403 395 402 398
哪台包装机包装的奶粉质量比较稳定?
它们的方差分别是
由 > 可知,乙包装机包装的奶粉质量比较稳定.
例1.某快餐公司的香辣鸡腿很受消费者欢迎.现有甲、乙两家农副产品加工厂到快餐公司推销鸡腿,两家鸡腿的价格相同,品质相近,快餐公司决定通过检查鸡腿的质量来确定选购哪
家的鸡腿.检查人员从两家的鸡腿中各随机抽取15个,记录它们的质量如下(单位:g)如下
表.根据表中的数据,你认为快餐公司应选购哪家工厂的鸡腿.
解:检查人员从甲、乙两家农副产品加工厂各随机抽取的15个鸡腿分别组成一个样本,样本数据的平均数分别是
样本数据的方差分别是
由 可知,两家加工厂的鸡腿质量大致相等;由 < 可知,甲加工厂的鸡腿质量更稳定,大小更均匀. 因此,快餐公司应该选购甲加工厂生产的鸡腿.
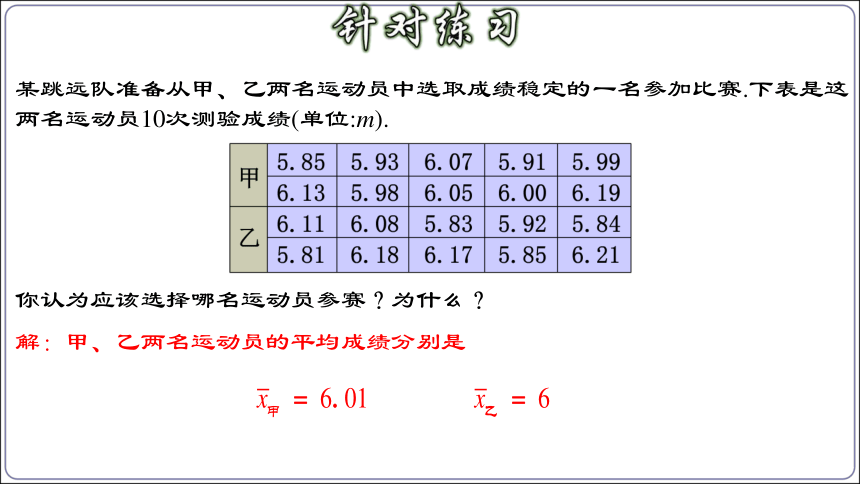
某跳远队准备从甲、乙两名运动员中选取成绩稳定的一名参加比赛.下表是这两名运动员10次测验成绩(单位:m).
你认为应该选择哪名运动员参赛?为什么?
解:甲、乙两名运动员的平均成绩分别是
它们的方差分别是
由 可知,甲、乙两名运动员的平均成绩大至相等;由 < 可知,甲的成绩更稳定.
如果要从中选出一人参加市级比赛,历届比赛表明,成绩达到5.92m就能夺冠,你认为应选谁参加比赛?如果历届比赛成绩表明,成绩达到6.08m就能打破记录,你认为又应该选谁参加这次比赛呢?
解:甲成绩更稳定,如果成绩达到5.92m就能夺冠,应选甲参赛;乙达到6.08m的可能性较大,如果成绩达到6.08m能打破纪录,应选乙参赛.
例2.在某旅游景区上山的一条小路上,有一些断断续续高低不等的台阶.如图是其中的甲、乙两段台阶路的示意图(图中数字表示每一阶的高度,单位:cm).哪段台阶路走起来更舒服?为什么?
21
20
21
19
19
20
甲
17
24
20
17
19
23
乙
分析:通过计算两段台阶的方差,比较波动性大小.
∴走甲台阶的波动性更,走起来更舒适.
解:
∵
例3.某校要从甲、乙两名跳远运动员中挑选一人参加一项校际比赛.在最近10次选拔赛中,他们的成绩(单位: cm)如下:
甲:585 596 610 598 612 597 604 600 613 601
乙:613 618 580 574 618 593 585 590 598 624
(1)这两名运动员的运动成绩各有何特点?
【分析】分别计算出平均数和方差;根据平均数判断出谁的成绩好,根据方差判断出谁的成绩波动大.
解:
(585+596+610+598+612+597+604+600+613+601)
=601.6,s2甲≈65.84;
(613+618+580+574+618+593+585+590+598+624)
=599.3,s2乙≈284.21.
由上面计算结果可知:甲队员的平均成绩较好,也比较稳定,乙队员的成绩相对不稳定.但甲队员的成绩不突出,乙队员和甲队员相比比较突出.
(2)历届比赛表明,成绩达到5.96m就很可能夺冠,你认为为了夺冠应选谁参加这项比赛?如果历届比赛成绩表明,成绩达到6.10m就能打破纪录,那么你认为为了打破纪录应选谁参加这项比赛.
解:从平均数分析可知,甲、乙两队员都有夺冠的可能.但由方差分析可知,甲成绩比较平稳,夺冠的可能性比乙大.
但要打破纪录,成绩要比较突出,因此乙队员打破纪录的可能性大,我认为为了打破纪录,应选乙队员参加这项比赛.
1.“恒盛”超市购进一批大米,大米的标准包装为每袋30kg,售货员任选6袋进行了称重检验,超过标准重量的记作“﹢”,不足标准重量的记作“﹣”,他记录的结果是+0.5,-0. 5,0,-0.5,-0.5,+1,那么这6袋大米重量的平均数和方差分别是( )
A.30,0.4 B.0, C.30, D.30.5,0.4
C
2.四名运动员参加了射击预选赛,他们成绩的平均环数及其方差s2如下表所示,如果选出一个成绩较好且状态稳定的人去参赛,那么应选( )
A.甲 B.乙 C.丙 D.丁
B
3.甲、乙两名同学进行射击训练,在相同条件下各射靶5次,命中环数统计如下:
甲:8,7,8,8,9 乙:9,7,5,10,9
(1)根据以上信息完成下表:
(2)如果乙再射击1次,命中8环,那么乙的射击成绩的方差________(填“变大”“变小”或“不变”).
变小
4.为了从甲、乙两名学生中选择一人参加电脑知识竞赛,在相同条件下对他们的电脑知识进行了10次测验,成绩如下,(单位:分):
(1)请填写下表:
(2)利用以上信息,请从两个不同的角度对甲、乙两名同学的成绩进行分析.
(2)利用以上信息,请从两个不同的角度对甲、乙两名同学的成绩进行分析.
解:甲成绩的众数是84,乙成绩的众数是90,从两人成绩的众数看,乙的成绩较好;甲成绩的方差是14.4,乙成绩的方差是38.4,从成绩的方差看,甲的成绩相对稳定.
5.两台机床同时生产直径是40mm的零件,为了鉴别机床性能好坏,检验产品的质量,从产品抽出10件进行测量(单位:mm),,结果如下表(超过40mm记为“+”,低于40mm记为“-”)所示:
问哪个机床性能更好些
解:样本数据的平均数分别是
它们的方差分别是
由 可知及 > 可知,乙机床的性能更好些.
6.甲、乙两位同学本学年每单元的测验成绩如下(单位:分)
甲:98,100,100,90,91,89, 99, 100, 100, 93
乙:98,99,94,95,92,92,98,96,99, 97
(1)他们的平均成绩分别是多少
(2)甲、乙的10次单元测验成绩的方差分别是多少
(3)这两位同学的成绩各有什么特点
(4)现要从中选出一人参加“希望杯”竞赛,历届比赛成绩表明,平时成绩达到98分以上才可能进入决赛,你认为应选谁参加这项竞赛,为什么
6.甲、乙两位同学本学年每单元的测验成绩如下(单位:分)
甲:98,100,100,90,91,89, 99, 100, 100, 93
乙:98,99,94,95,92,92,98,96,99, 97
(1)他们的平均成绩分别是多少
解: (1) 他们的平均成绩分别是
6.甲、乙两位同学本学年每单元的测验成绩如下(单位:分)
甲:98,100,100,90,91,89, 99, 100, 100, 93
乙:98,99,94,95,92,92,98,96,99, 97
(2)甲、乙的10次单元测验成绩的方差分别是多少
(2)甲、 乙的10次单元测验成绩的方差分别是
6.甲、乙两位同学本学年每单元的测验成绩如下(单位:分)
甲:98,100,100,90,91,89, 99, 100, 100, 93
乙:98,99,94,95,92,92,98,96,99, 97
(3)这两位同学的成绩各有什么特点
(3) 两位同学的平均成绩相同;乙的方差小于甲的方差,故乙的成绩比甲更稳定;甲虽然成绩不稳定,但发挥好时成绩比乙优秀.
6.甲、乙两位同学本学年每单元的测验成绩如下(单位:分)
甲:98,100,100,90,91,89, 99, 100, 100, 93
乙:98,99,94,95,92,92,98,96,99, 97
(4)现要从中选出一人参加“希望杯”竞赛,历届比赛成绩表明,平时成绩达到98分以上才可能进入决赛,你认为应选谁参加这项竞赛,为什么
(4) 选甲去,因为甲的成绩有6次达到98分以上,而乙只有4次.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
