第九章 不等式与不等式组 章节复习【2024春人教七下数学精品课件含动画】
文档属性
| 名称 | 第九章 不等式与不等式组 章节复习【2024春人教七下数学精品课件含动画】 |  | |
| 格式 | pptx | ||
| 文件大小 | 7.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-03 09:47:50 | ||
图片预览








文档简介
(共62张PPT)
人教七下数学同步精品课件
人教版七年级下册
情境引入
学习目标
知识精讲
典例解析
针对练习
总结提升
达标检测
小结梳理
2024春人教版七(下)数学同步精品课件
第九章 章节复习
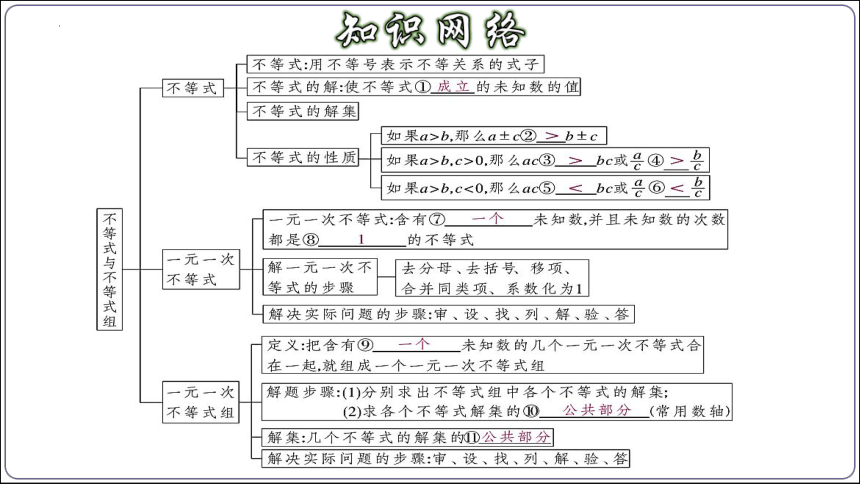
第九章 不等式与不等式组
1.巩固运用不等式的性质; (重点)
2.会解简单的一元一次不等式(组),并能在数轴上表示出解集;(重点)
3.能够根据具体问题中的数量关系,列出一元一次不等式(组), 解决简单的实际问题. (难点)
像<和x>50这样用符号“<”或“>”表示大小关系的式子,叫做不等式.
(1)像a+2≠a-2这样用符号“≠”表示不等关系的式子也是不等式.
(2)不等式中可以含未知数,也可以不含未知数.例如:a+2>5,4b<6;
3<4,-1>-2.
(3)“≥”读作“大于或等于”或“不小于”
“≤”读作“小于或等于”或“不大于”
一、不等式的相关概念
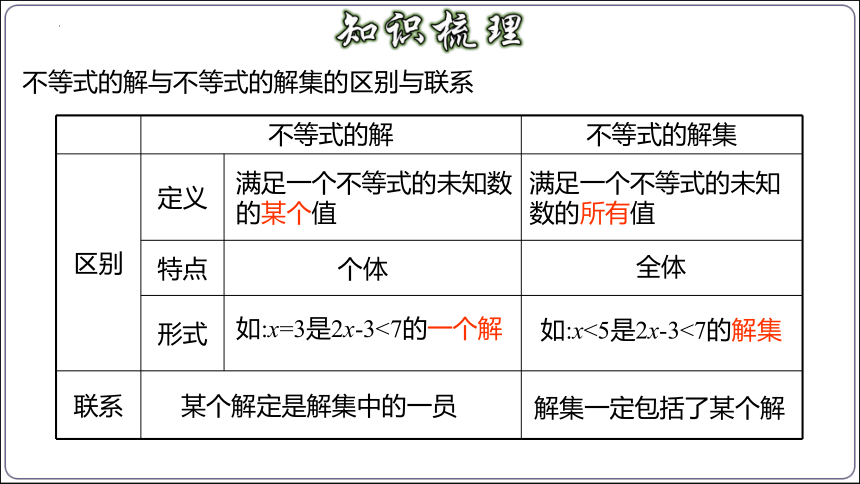
使不等式成立的未知数的值叫做不等式的解.
一般地,一个含有未知数的不等式的所有的解,组成这个不等式的解集.求不等式的解集的过程叫做解不等式.
不等式的解 不等式的解集
区别 定义
特点
形式
联系
满足一个不等式的未知数的某个值
满足一个不等式的未知数的所有值
个体
全体
如:x=3是2x-3<7的一个解
如:x<5是2x-3<7的解集
某个解定是解集中的一员
解集一定包括了某个解
不等式的解与不等式的解集的区别与联系
不等式的性质1:不等式两边加(或减)同一个数(或式子),不等号的方向不变.
如果 a>b,那么 a±c>b±c.
不等式的性质2:不等式两边乘(或除以)同一个正数,不等号的方向不变.
如果 a>b,c>0,那么 ac>bc (或> ).
不等式的性质3:不等式两边乘(或除以)同一个负数,不等号的方向改变.
如果 a>b,c<0,那么 ac<bc (或< ).
二、不等式的性质
类似于一元一次方程,含有一个未知数,未知数的次数是1的不等式,叫做一元一次不等式.
1.解一元一次方程,要根据等式的性质,将方程逐步化为x=a的形式;而解一元一次不等式,则要根据不等式的性质,将不等式逐步化为x<a或x>a的形式.
2.解一元一次不等式与解一元一次方程一样,都是通过“去分母、去括号、移项、合并同类项、系数化为1”几个步骤确定答案.
3.如果未知数的系数为负数,那么在系数化为1时,要改变不等号的方向.
4.在数轴上表示不等式的解集,大于向右画线,小于向左画线,界点有等号画实心圆点,无等号画空心圆圈.
★解一元一次不等式的基本要求:
三、一元一次不等式及其解法
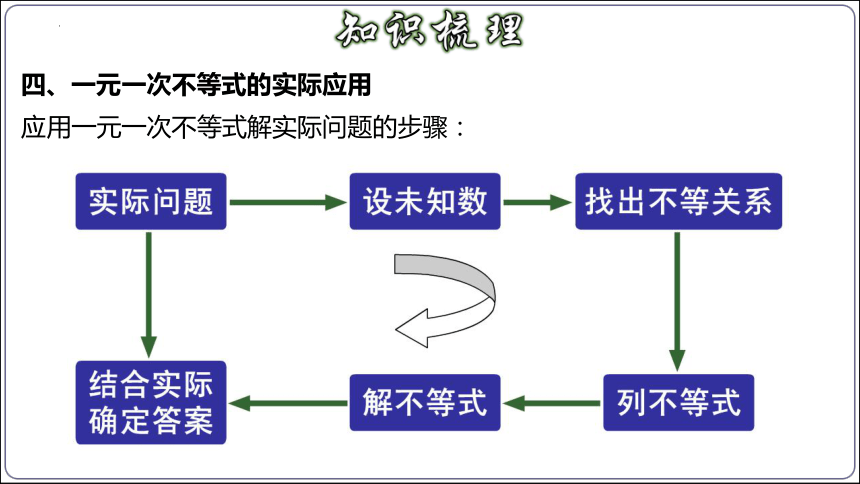
应用一元一次不等式解实际问题的步骤:
四、一元一次不等式的实际应用
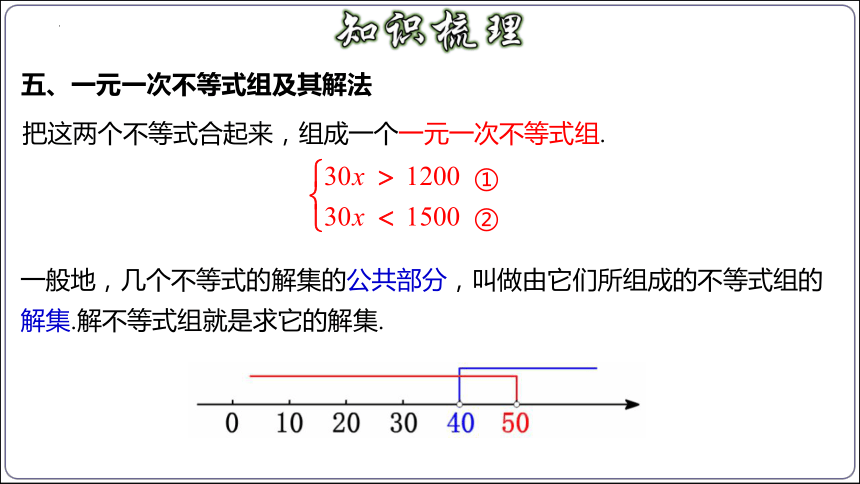
五、一元一次不等式组及其解法
把这两个不等式合起来,组成一个一元一次不等式组.
①
②
一般地,几个不等式的解集的公共部分,叫做由它们所组成的不等式组的解集.解不等式组就是求它的解集.
一元一次不等式组的解集图析(a>b)
应用一元一次不等式组解实际问题的步骤:
六、一元一次不等式组的实际应用
01
不等式的相关概念与性质
例1.下列式子中,一元一次不等式有( )
① 3x-1≥4; ② 2+3x>6; ③ 3-<5; ④ >0;
⑤ ; ⑥ x+xy≥y2; ⑦ x>0.
A.5个 B.4个 C.6个 D.3个
A
例2.若,则下列不等式一定成立的是( )
A. B.C. D.
【分析】解:A.则,故该选项不成立,不符合题意;
B.,则,故该选项成立,符合题意;
C.,不能判断,故该选项不成立,不符合题意;
D.,当时,;当时,;故该选项不成立,不符合题意.
B
【1-1】设 a>b,用“>”或“<”填空,并说出根据哪条性质.
(1) a+4___b+4;________________ (2) a-1___b-1;________________
(3) -3a___-3b; ________________ (4) ___; ________________
(5) 2a-5___2b-5; _____________________
(6) -3a+2___-3b+2;_____________________
(7) +1___ +1; _____________________
不等式基本性质1
不等式基本性质1
不等式基本性质3
不等式基本性质2
不等式基本性质2及1
不等式基本性质3及1
不等式基本性质2及1
>
<
>
>
>
<
>
【1-2】若,且,则的取值范围是_______.
【分析】∵不等式(a﹣3)xa﹣3的解集为x≤1,
∴,
解得:.
【1-3】下列说法中错误的是( )
A.若,则 B.若,则
C.若,则 D.若,则
C
【分析】解:若,则,正确,不合题意;
若,则,正确,不合题意;
若,当时,,错误,符合题意;
若,则,正确,不合题意.
例3.解下列不等式,并在数轴上表示解集:
(1) 5x+15>4x-1 (2) 2(x+5)≤3(x-5) (3) (4)
解:(1)移项,得 5x-4x>-1-15
合并同类项,得 x>-16
解:(2)去括号,得 2x+10≤3x-15
移项,得 2x-3x≤-15-10
合并同类项,得 -x≤-25
系数化为1,得 x≥25
02
解一元一次不等式
例3.解下列不等式,并在数轴上表示解集:
(1) 5x+15>4x-1 (2) 2(x+5)≤3(x-5) (3) (4)
解:(3)去分母,得 3(x-1)<7(2x+5)
去括号,得 3x-3<14x+35
移项,得 3x-14x<35+3
合并同类项,得 -11x<38
系数化为1,得 x>-
解:(4)去分母,得 2(x+1)≥3(2x-5)+12
去括号,得 2x+2≥6x-15+12
移项,得 2x-6x≥-15+12-2
合并同类项,得 -4x≥-5
系数化为1,得 x≤
例4.若关于x,y的二元一次方程组的解满足,求m的取值范围.
解:,
由得:,
由得:,
,
,
解得.
【2-1】在解不等式当 - ≤1时,去分母正确的是( )
A. 2x-3x-3≤6 B.2x-3(x-1)≤6 C.2x-3x-3≤1 D.2x-3(x-1)≤1
【2-2】关于x的不等式3x-a≤0, 只有两个正整数解,则a的取值范围是___________.
B
6≤m<9
【2-3】解不等式,并把它的解集在数轴上表示出来.
(1); (2);
(1)解:去括号得:,
移项得:,
合并同类项得:,
化系数为1得:;
(2)解:去分母得:,
去括号得:,
移项得:,
合并同类项得:,
化系数为1得:;
【2-3】解不等式,并把它的解集在数轴上表示出来.
(3)(4)
(3)解:移项得:,
合并同类项得:,
化系数为1得:;
(4)解:去括号得:,
移项得:,
合并同类项得:,
化系数为1得:.
03
一元一次不等式的应用
例5.某工程队计划在10天内修路6km,施工前2天修完1.2km后,计划发生变化,准备提前2天完成修路任务,以后几天内平均每天至少要修路多少?
解:设以后几天内平均每天修路xkm.依题意得
(10-2-2)x+1.2≥6
解得 x≥0.8
答:以后几天内平均每天至少要修路0.8km.
例6.甲、乙两商场以同样价格出售同样的商品,并且又各自推出不同的优惠方案:在甲商场累计购物超过100元后,超出100元的部分按90%收费;在乙商场累计购物超过50元后,超出50元的部分按95%收费.顾客到哪家商场购物花费少?
例6.甲、乙两商场以同样价格出售同样的商品,并且又各自推出不同的优惠方案:在甲商场累计购物超过100元后,超出100元的部分按90%收费;在乙商场累计购物超过50元后,超出50元的部分按95%收费.顾客到哪家商场购物花费少?
分析:在甲商场购物超过100元后享受优惠,在乙商场购物超过50元后享受优惠.因此,我们需要分三种情况讨论:
(1)累计购物不超过50元;
(2)累计购物超过50元而不超过100元;
(3)累计购物超过100元.
例6.甲、乙两商场以同样价格出售同样的商品,并且又各自推出不同的优惠方案:在甲商场累计购物超过100元后,超出100元的部分按90%收费;在乙商场累计购物超过50元后,超出50元的部分按95%收费.顾客到哪家商场购物花费少?
解:(1)当累计购物不超过50元时,在甲、乙两商场购物都不享受优惠,且两商场以同样价格出售同样的商品,因此到两商场购物花费一样.
(2)当累计购物超过50元而不超过100元时,享受乙商场优惠,不享受甲商场优惠,因此到乙商场购物花费少.
例6.甲、乙两商场以同样价格出售同样的商品,并且又各自推出不同的优惠方案:在甲商场累计购物超过100元后,超出100元的部分按90%收费;在乙商场累计购物超过50元后,超出50元的部分按95%收费.顾客到哪家商场购物花费少?
(3)当累计购物超过100元时,设累计购物x元.(x>100)依题意,得
①若到甲商场购物花费少,则
50+0.95(x-50)>100+0.9(x-100)
解得 x>150
这就是说,累计购物超过150元时,到甲商场购物花费少.
例6.甲、乙两商场以同样价格出售同样的商品,并且又各自推出不同的优惠方案:在甲商场累计购物超过100元后,超出100元的部分按90%收费;在乙商场累计购物超过50元后,超出50元的部分按95%收费.顾客到哪家商场购物花费少?
(3)当累计购物超过100元时,设累计购物x元.(x>100)依题意,得
②若到乙商场购物花费少,则
50+0.95(x-50)<100+0.9(x-100)
解得 x<150
这就是说,累计购物超过100元而不到150元时,到乙商场购物花费少.
例6.甲、乙两商场以同样价格出售同样的商品,并且又各自推出不同的优惠方案:在甲商场累计购物超过100元后,超出100元的部分按90%收费;在乙商场累计购物超过50元后,超出50元的部分按95%收费.顾客到哪家商场购物花费少?
(3)当累计购物超过100元时,设累计购物x元.(x>100)依题意,得
③若50+0.95(x-50)=100+0.9(x-100)
解得 x=150
这就是说,累计购物为150元时,到甲、乙商场购物花费一样.
【3-1】某种商品的进价为800元,出售时标价为1200元,后来由于该商品积压,商店准备打折出售,但要保持利润率不低于5%,则至多可打( )
A.6折 B.7折 C.8折 D.9折
【3-2】某种出租车的收费标准:起步价7元(即行驶距离不超过3千米都需付7元车费),超过3千米后,每增加1千米,加收2. 4元(不足1千米按1千米计).某人乘这种出租车从甲地到乙地共付车费19元,那么甲地到乙地路程的最大值是( )
A. 5千米 B.7千米 C.8千米 D. 15千米
B
C
【3-3】学校为想购买计算器的学生联系了两家公司,两家公司的报价均为50元/个,并且质量和服务承诺相同,且都表示对学生优惠:甲公司表示每个计算器9折出售;乙公司表示购买100个以上,超过100个的部分按8折收费.假如你是校方,你该怎样选择这两家公司
解:设学校集体购买的计算器为x个,依题意得
(1)显然当x≤100时,选择甲公司合算.
(2)当x>100时, ①如果选甲公司合算,则有
0.9×50x<100×50+ (x-100) ×0.8×50
解得 x<200
∴当购买个数超过100而不超过200时,选甲公司合算.
【3-3】学校为想购买计算器的学生联系了两家公司,两家公司的报价均为50元/个,并且质量和服务承诺相同,且都表示对学生优惠:甲公司表示每个计算器9折出售;乙公司表示购买100个以上,超过100个的部分按8折收费.假如你是校方,你该怎样选择这两家公司
(2)当x>100时,
②如果选乙公司合算,则有
0.9×50x>100×50+ (x-100)×0. 8×50
解得 x>200
∴当购买个数超过200时,选乙公司合算.
【3-3】学校为想购买计算器的学生联系了两家公司,两家公司的报价均为50元/个,并且质量和服务承诺相同,且都表示对学生优惠:甲公司表示每个计算器9折出售;乙公司表示购买100个以上,超过100个的部分按8折收费.假如你是校方,你该怎样选择这两家公司
(2)当x>100时,
③如果甲、乙两家公司费用相同,则有
0.9×50x=100×50+ (x-100) × 0.8×50
解得 x=200
∴当购买个数为200时,选择甲、乙两公司都一样.
04
一元一次不等式组的解法
例7.解下列不等式组:
(1) (2) (3)
①
②
①
②
①
②
解:(1)解不等式①,得 x>
解不等式②,得 x>1
∴ 不等式组的解集是 x>1.
解:(2)解不等式①,得 x<-6
解不等式②,得 x>2
∴ 不等式组无解.
例7.解下列不等式组:
(1) (2) (3)
①
②
①
②
①
②
解:(3)解不等式①,得 x>-2.4
解不等式②,得 x≤3.5
∴ 不等式组的解集是 -2.4<x≤3.5
解:解不等式组
解不等式①,得 x>-
解不等式②,得 x≤4
∴ 不等式组的解集是 -<x≤4
∴ x可取的整数值是-2,-1,0,1,2,3,4.
例8.x取哪些整数值时,不等式5x+2>3(x-1)与x-1≤7-x都成立?
【4-1】不等式组的解集在数轴上表示出来如图所示:
则这个不等式组为( )
A. B. C.D.
C
【4-2】解下列不等式组:
(1) (2)
解:不等式①的解集: ,
不等式②的解集: ,
∴不等式组的解集为.
解:不等式①的解集:,
不等式②的解集:,
则不等式组的解集为.
【4-3】x取哪些正整数值时,不等式x+3>6与2x-1<10都成立?
解:解不等式组
解不等式①,得 x>3
解不等式②,得 x<5.5
∴ 不等式组的解集是 3<x<5.5
∴ x可取的正整数值是4,5.
例9.若关于x的不等式组只有4个整数解,求a的取值范围.
05
一元一次不等式组的解法典型应用
解:
解不等式①,得,
解不等式②,得,
∵此不等式组只有4个整数解,
例9.若关于x的不等式组只有4个整数解,求a的取值范围.
∴此不等式组的解集为,
∴它的4个整数解为20、19、18、17,
∴,
解得a的取值范围是:.
例10.若不等式组有解,求实数a的取值范围.
解:解不等式,得
解不等式,得
原不等式组有解,则
解得
例11.已知关于的不等式组解集为,求代数式的值.
解: ,由得,;由得,,
∴,
∵,
∴,,
例11.已知关于的不等式组解集为,求代数式的值.
∴,,
∴,
∴.
【5-1】已知不等式组无解,求m的取值范围.
解:,
由①得,x>8,
∵不等式组无解,
∴8≥4m,
解得:m≤2,
∴m的取值范围是m≤2.
【5-2】已知方程组的解、满足,求的取值范围.
解: ,
得,,即,
,
,
解得.
【5-3】已知关于x的不等式组有四个整数解,求实数a的取值范围.
解:
解不等式①得:,
解不等式②得:
∴
∵不等式组有四个整数解,∴整数解是,,0,1,
∴∴
06
用一元一次不等式组解决实际问题
例12.某班有若干学生住宿,若每间住4人,则有20人没宿舍住;若每间住8人则有一间没有住满人,试求该班宿舍间数及住宿人数?
解:设有x间宿舍,则有(4x+20)人住宿,依题意可得
解得5< x<7
因为宿舍间数是整数;
所以x=6.
住宿人数:4x+20=44(人)
答:该班有6间宿舍及44人住宿.
例13.某超市计划同时购进一批甲、乙两种商品,若购进甲商品10件和乙商品8件,共需要资金880元;若购进甲商品2件和乙商品5件,共需要资金380元.
(1)求甲、乙两种商品每件的进价各是多少元?
(2)该超市计划购进这两种商品共50件,而可用于购买这两种商品的资金不超过2520元.根据市场行情,销售一件甲商品可获利10元,销售一件乙商品可获利15元.该超市希望销售完这两种商品所获利润不少于620元.则该超市有哪几种进货方案?
(1)解:设甲商品每件的进价是元,乙商品每件的进价是元,根据题意得,
解得:
答:甲商品每件的进价是元,乙商品每件的进价是元;
(2)解:设购进甲商品件,则购进乙商品件,根据题意得,
解得:
∵为正整数,故
∴有三种进货方案,
方案一:购进甲商品件,乙商品件;
方案二:购进甲商品件,乙商品件;
方案三:购进甲商品件,乙商品件.
【6-1】为了美化环境,张老师组织班级部分同学在操场植树,班级购买了若干树苗,若每人植棵,还剩棵,若每人植棵,最后一人有树植,但不足棵,这批树苗共有多少棵?
解:设共有人参与植树,则这批树苗共有棵,依题意得:
解得:.
又为正整数,
,
. 答:这批树苗共有棵.
【6-2】甲以5千米/时的速度进行有氧体育锻炼,2小时后,乙骑自行车从同一地出发沿同一条路追赶甲,根据他们两人的约定,乙最快不早于1小时追上甲,最慢不晚于1小时15分追上甲.那么乙骑车的速度应当控制在什么范围
解:设乙骑车的速度为x千米/时,依题意得
解这个不等式组,得13≤x≤15
答:乙骑车的速度应控制在13~15千米/时这个范围内.
【6-3】为了美化环境,园林部门决定利用现有的3490盆甲种花卉和2950盆乙种花卉搭配A、B两种园艺造型共50个摆放在迎宾大道两侧,已知搭配一个A种造型需甲种花卉80盆,乙种花卉40盆,搭配一个B种造型需甲种花卉50盆,乙种花卉90盆.
(1)某校七年级(1)班课外活动小组承接了这个园艺造型搭配方案的设计,问符合题意的搭配方案有几种 请你帮助设计出来.
(2)若搭配一个A种造型的成本是800元,搭配一个B种造型的成本是960元,试说明(1)中哪种方案成本最低 最低成本是多少元
解: (1) 设搭配A种造型x个,则B种造型为(50-x)个,依题意得
解这个不等式组得31≤x≤33
∵x是整数,
∴x可取31、32、 33
∴可设计三种搭配方案:
①A种园艺造型31个,B种园艺造型19个;
②A种园艺造型32个,B种园艺造型18个;
③A种园艺造型33个,B种园艺造型17个.
(2) 方案①需成本: 31×800+ 19×960=43040(元);
方案②需成本: 32×800+ 18×960=42880(元) ;
方案③需成本: 33×800+ 17×960=42720(元).
应选择方案③,成本最低,最低成本为42720元.
(2)若搭配一个A种造型的成本是800元,搭配一个B种造型的成本是960元,试说明(1)中哪种方案成本最低 最低成本是多少元
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
人教七下数学同步精品课件
人教版七年级下册
情境引入
学习目标
知识精讲
典例解析
针对练习
总结提升
达标检测
小结梳理
2024春人教版七(下)数学同步精品课件
第九章 章节复习
第九章 不等式与不等式组
1.巩固运用不等式的性质; (重点)
2.会解简单的一元一次不等式(组),并能在数轴上表示出解集;(重点)
3.能够根据具体问题中的数量关系,列出一元一次不等式(组), 解决简单的实际问题. (难点)
像<和x>50这样用符号“<”或“>”表示大小关系的式子,叫做不等式.
(1)像a+2≠a-2这样用符号“≠”表示不等关系的式子也是不等式.
(2)不等式中可以含未知数,也可以不含未知数.例如:a+2>5,4b<6;
3<4,-1>-2.
(3)“≥”读作“大于或等于”或“不小于”
“≤”读作“小于或等于”或“不大于”
一、不等式的相关概念
使不等式成立的未知数的值叫做不等式的解.
一般地,一个含有未知数的不等式的所有的解,组成这个不等式的解集.求不等式的解集的过程叫做解不等式.
不等式的解 不等式的解集
区别 定义
特点
形式
联系
满足一个不等式的未知数的某个值
满足一个不等式的未知数的所有值
个体
全体
如:x=3是2x-3<7的一个解
如:x<5是2x-3<7的解集
某个解定是解集中的一员
解集一定包括了某个解
不等式的解与不等式的解集的区别与联系
不等式的性质1:不等式两边加(或减)同一个数(或式子),不等号的方向不变.
如果 a>b,那么 a±c>b±c.
不等式的性质2:不等式两边乘(或除以)同一个正数,不等号的方向不变.
如果 a>b,c>0,那么 ac>bc (或> ).
不等式的性质3:不等式两边乘(或除以)同一个负数,不等号的方向改变.
如果 a>b,c<0,那么 ac<bc (或< ).
二、不等式的性质
类似于一元一次方程,含有一个未知数,未知数的次数是1的不等式,叫做一元一次不等式.
1.解一元一次方程,要根据等式的性质,将方程逐步化为x=a的形式;而解一元一次不等式,则要根据不等式的性质,将不等式逐步化为x<a或x>a的形式.
2.解一元一次不等式与解一元一次方程一样,都是通过“去分母、去括号、移项、合并同类项、系数化为1”几个步骤确定答案.
3.如果未知数的系数为负数,那么在系数化为1时,要改变不等号的方向.
4.在数轴上表示不等式的解集,大于向右画线,小于向左画线,界点有等号画实心圆点,无等号画空心圆圈.
★解一元一次不等式的基本要求:
三、一元一次不等式及其解法
应用一元一次不等式解实际问题的步骤:
四、一元一次不等式的实际应用
五、一元一次不等式组及其解法
把这两个不等式合起来,组成一个一元一次不等式组.
①
②
一般地,几个不等式的解集的公共部分,叫做由它们所组成的不等式组的解集.解不等式组就是求它的解集.
一元一次不等式组的解集图析(a>b)
应用一元一次不等式组解实际问题的步骤:
六、一元一次不等式组的实际应用
01
不等式的相关概念与性质
例1.下列式子中,一元一次不等式有( )
① 3x-1≥4; ② 2+3x>6; ③ 3-<5; ④ >0;
⑤ ; ⑥ x+xy≥y2; ⑦ x>0.
A.5个 B.4个 C.6个 D.3个
A
例2.若,则下列不等式一定成立的是( )
A. B.C. D.
【分析】解:A.则,故该选项不成立,不符合题意;
B.,则,故该选项成立,符合题意;
C.,不能判断,故该选项不成立,不符合题意;
D.,当时,;当时,;故该选项不成立,不符合题意.
B
【1-1】设 a>b,用“>”或“<”填空,并说出根据哪条性质.
(1) a+4___b+4;________________ (2) a-1___b-1;________________
(3) -3a___-3b; ________________ (4) ___; ________________
(5) 2a-5___2b-5; _____________________
(6) -3a+2___-3b+2;_____________________
(7) +1___ +1; _____________________
不等式基本性质1
不等式基本性质1
不等式基本性质3
不等式基本性质2
不等式基本性质2及1
不等式基本性质3及1
不等式基本性质2及1
>
<
>
>
>
<
>
【1-2】若,且,则的取值范围是_______.
【分析】∵不等式(a﹣3)xa﹣3的解集为x≤1,
∴,
解得:.
【1-3】下列说法中错误的是( )
A.若,则 B.若,则
C.若,则 D.若,则
C
【分析】解:若,则,正确,不合题意;
若,则,正确,不合题意;
若,当时,,错误,符合题意;
若,则,正确,不合题意.
例3.解下列不等式,并在数轴上表示解集:
(1) 5x+15>4x-1 (2) 2(x+5)≤3(x-5) (3) (4)
解:(1)移项,得 5x-4x>-1-15
合并同类项,得 x>-16
解:(2)去括号,得 2x+10≤3x-15
移项,得 2x-3x≤-15-10
合并同类项,得 -x≤-25
系数化为1,得 x≥25
02
解一元一次不等式
例3.解下列不等式,并在数轴上表示解集:
(1) 5x+15>4x-1 (2) 2(x+5)≤3(x-5) (3) (4)
解:(3)去分母,得 3(x-1)<7(2x+5)
去括号,得 3x-3<14x+35
移项,得 3x-14x<35+3
合并同类项,得 -11x<38
系数化为1,得 x>-
解:(4)去分母,得 2(x+1)≥3(2x-5)+12
去括号,得 2x+2≥6x-15+12
移项,得 2x-6x≥-15+12-2
合并同类项,得 -4x≥-5
系数化为1,得 x≤
例4.若关于x,y的二元一次方程组的解满足,求m的取值范围.
解:,
由得:,
由得:,
,
,
解得.
【2-1】在解不等式当 - ≤1时,去分母正确的是( )
A. 2x-3x-3≤6 B.2x-3(x-1)≤6 C.2x-3x-3≤1 D.2x-3(x-1)≤1
【2-2】关于x的不等式3x-a≤0, 只有两个正整数解,则a的取值范围是___________.
B
6≤m<9
【2-3】解不等式,并把它的解集在数轴上表示出来.
(1); (2);
(1)解:去括号得:,
移项得:,
合并同类项得:,
化系数为1得:;
(2)解:去分母得:,
去括号得:,
移项得:,
合并同类项得:,
化系数为1得:;
【2-3】解不等式,并把它的解集在数轴上表示出来.
(3)(4)
(3)解:移项得:,
合并同类项得:,
化系数为1得:;
(4)解:去括号得:,
移项得:,
合并同类项得:,
化系数为1得:.
03
一元一次不等式的应用
例5.某工程队计划在10天内修路6km,施工前2天修完1.2km后,计划发生变化,准备提前2天完成修路任务,以后几天内平均每天至少要修路多少?
解:设以后几天内平均每天修路xkm.依题意得
(10-2-2)x+1.2≥6
解得 x≥0.8
答:以后几天内平均每天至少要修路0.8km.
例6.甲、乙两商场以同样价格出售同样的商品,并且又各自推出不同的优惠方案:在甲商场累计购物超过100元后,超出100元的部分按90%收费;在乙商场累计购物超过50元后,超出50元的部分按95%收费.顾客到哪家商场购物花费少?
例6.甲、乙两商场以同样价格出售同样的商品,并且又各自推出不同的优惠方案:在甲商场累计购物超过100元后,超出100元的部分按90%收费;在乙商场累计购物超过50元后,超出50元的部分按95%收费.顾客到哪家商场购物花费少?
分析:在甲商场购物超过100元后享受优惠,在乙商场购物超过50元后享受优惠.因此,我们需要分三种情况讨论:
(1)累计购物不超过50元;
(2)累计购物超过50元而不超过100元;
(3)累计购物超过100元.
例6.甲、乙两商场以同样价格出售同样的商品,并且又各自推出不同的优惠方案:在甲商场累计购物超过100元后,超出100元的部分按90%收费;在乙商场累计购物超过50元后,超出50元的部分按95%收费.顾客到哪家商场购物花费少?
解:(1)当累计购物不超过50元时,在甲、乙两商场购物都不享受优惠,且两商场以同样价格出售同样的商品,因此到两商场购物花费一样.
(2)当累计购物超过50元而不超过100元时,享受乙商场优惠,不享受甲商场优惠,因此到乙商场购物花费少.
例6.甲、乙两商场以同样价格出售同样的商品,并且又各自推出不同的优惠方案:在甲商场累计购物超过100元后,超出100元的部分按90%收费;在乙商场累计购物超过50元后,超出50元的部分按95%收费.顾客到哪家商场购物花费少?
(3)当累计购物超过100元时,设累计购物x元.(x>100)依题意,得
①若到甲商场购物花费少,则
50+0.95(x-50)>100+0.9(x-100)
解得 x>150
这就是说,累计购物超过150元时,到甲商场购物花费少.
例6.甲、乙两商场以同样价格出售同样的商品,并且又各自推出不同的优惠方案:在甲商场累计购物超过100元后,超出100元的部分按90%收费;在乙商场累计购物超过50元后,超出50元的部分按95%收费.顾客到哪家商场购物花费少?
(3)当累计购物超过100元时,设累计购物x元.(x>100)依题意,得
②若到乙商场购物花费少,则
50+0.95(x-50)<100+0.9(x-100)
解得 x<150
这就是说,累计购物超过100元而不到150元时,到乙商场购物花费少.
例6.甲、乙两商场以同样价格出售同样的商品,并且又各自推出不同的优惠方案:在甲商场累计购物超过100元后,超出100元的部分按90%收费;在乙商场累计购物超过50元后,超出50元的部分按95%收费.顾客到哪家商场购物花费少?
(3)当累计购物超过100元时,设累计购物x元.(x>100)依题意,得
③若50+0.95(x-50)=100+0.9(x-100)
解得 x=150
这就是说,累计购物为150元时,到甲、乙商场购物花费一样.
【3-1】某种商品的进价为800元,出售时标价为1200元,后来由于该商品积压,商店准备打折出售,但要保持利润率不低于5%,则至多可打( )
A.6折 B.7折 C.8折 D.9折
【3-2】某种出租车的收费标准:起步价7元(即行驶距离不超过3千米都需付7元车费),超过3千米后,每增加1千米,加收2. 4元(不足1千米按1千米计).某人乘这种出租车从甲地到乙地共付车费19元,那么甲地到乙地路程的最大值是( )
A. 5千米 B.7千米 C.8千米 D. 15千米
B
C
【3-3】学校为想购买计算器的学生联系了两家公司,两家公司的报价均为50元/个,并且质量和服务承诺相同,且都表示对学生优惠:甲公司表示每个计算器9折出售;乙公司表示购买100个以上,超过100个的部分按8折收费.假如你是校方,你该怎样选择这两家公司
解:设学校集体购买的计算器为x个,依题意得
(1)显然当x≤100时,选择甲公司合算.
(2)当x>100时, ①如果选甲公司合算,则有
0.9×50x<100×50+ (x-100) ×0.8×50
解得 x<200
∴当购买个数超过100而不超过200时,选甲公司合算.
【3-3】学校为想购买计算器的学生联系了两家公司,两家公司的报价均为50元/个,并且质量和服务承诺相同,且都表示对学生优惠:甲公司表示每个计算器9折出售;乙公司表示购买100个以上,超过100个的部分按8折收费.假如你是校方,你该怎样选择这两家公司
(2)当x>100时,
②如果选乙公司合算,则有
0.9×50x>100×50+ (x-100)×0. 8×50
解得 x>200
∴当购买个数超过200时,选乙公司合算.
【3-3】学校为想购买计算器的学生联系了两家公司,两家公司的报价均为50元/个,并且质量和服务承诺相同,且都表示对学生优惠:甲公司表示每个计算器9折出售;乙公司表示购买100个以上,超过100个的部分按8折收费.假如你是校方,你该怎样选择这两家公司
(2)当x>100时,
③如果甲、乙两家公司费用相同,则有
0.9×50x=100×50+ (x-100) × 0.8×50
解得 x=200
∴当购买个数为200时,选择甲、乙两公司都一样.
04
一元一次不等式组的解法
例7.解下列不等式组:
(1) (2) (3)
①
②
①
②
①
②
解:(1)解不等式①,得 x>
解不等式②,得 x>1
∴ 不等式组的解集是 x>1.
解:(2)解不等式①,得 x<-6
解不等式②,得 x>2
∴ 不等式组无解.
例7.解下列不等式组:
(1) (2) (3)
①
②
①
②
①
②
解:(3)解不等式①,得 x>-2.4
解不等式②,得 x≤3.5
∴ 不等式组的解集是 -2.4<x≤3.5
解:解不等式组
解不等式①,得 x>-
解不等式②,得 x≤4
∴ 不等式组的解集是 -<x≤4
∴ x可取的整数值是-2,-1,0,1,2,3,4.
例8.x取哪些整数值时,不等式5x+2>3(x-1)与x-1≤7-x都成立?
【4-1】不等式组的解集在数轴上表示出来如图所示:
则这个不等式组为( )
A. B. C.D.
C
【4-2】解下列不等式组:
(1) (2)
解:不等式①的解集: ,
不等式②的解集: ,
∴不等式组的解集为.
解:不等式①的解集:,
不等式②的解集:,
则不等式组的解集为.
【4-3】x取哪些正整数值时,不等式x+3>6与2x-1<10都成立?
解:解不等式组
解不等式①,得 x>3
解不等式②,得 x<5.5
∴ 不等式组的解集是 3<x<5.5
∴ x可取的正整数值是4,5.
例9.若关于x的不等式组只有4个整数解,求a的取值范围.
05
一元一次不等式组的解法典型应用
解:
解不等式①,得,
解不等式②,得,
∵此不等式组只有4个整数解,
例9.若关于x的不等式组只有4个整数解,求a的取值范围.
∴此不等式组的解集为,
∴它的4个整数解为20、19、18、17,
∴,
解得a的取值范围是:.
例10.若不等式组有解,求实数a的取值范围.
解:解不等式,得
解不等式,得
原不等式组有解,则
解得
例11.已知关于的不等式组解集为,求代数式的值.
解: ,由得,;由得,,
∴,
∵,
∴,,
例11.已知关于的不等式组解集为,求代数式的值.
∴,,
∴,
∴.
【5-1】已知不等式组无解,求m的取值范围.
解:,
由①得,x>8,
∵不等式组无解,
∴8≥4m,
解得:m≤2,
∴m的取值范围是m≤2.
【5-2】已知方程组的解、满足,求的取值范围.
解: ,
得,,即,
,
,
解得.
【5-3】已知关于x的不等式组有四个整数解,求实数a的取值范围.
解:
解不等式①得:,
解不等式②得:
∴
∵不等式组有四个整数解,∴整数解是,,0,1,
∴∴
06
用一元一次不等式组解决实际问题
例12.某班有若干学生住宿,若每间住4人,则有20人没宿舍住;若每间住8人则有一间没有住满人,试求该班宿舍间数及住宿人数?
解:设有x间宿舍,则有(4x+20)人住宿,依题意可得
解得5< x<7
因为宿舍间数是整数;
所以x=6.
住宿人数:4x+20=44(人)
答:该班有6间宿舍及44人住宿.
例13.某超市计划同时购进一批甲、乙两种商品,若购进甲商品10件和乙商品8件,共需要资金880元;若购进甲商品2件和乙商品5件,共需要资金380元.
(1)求甲、乙两种商品每件的进价各是多少元?
(2)该超市计划购进这两种商品共50件,而可用于购买这两种商品的资金不超过2520元.根据市场行情,销售一件甲商品可获利10元,销售一件乙商品可获利15元.该超市希望销售完这两种商品所获利润不少于620元.则该超市有哪几种进货方案?
(1)解:设甲商品每件的进价是元,乙商品每件的进价是元,根据题意得,
解得:
答:甲商品每件的进价是元,乙商品每件的进价是元;
(2)解:设购进甲商品件,则购进乙商品件,根据题意得,
解得:
∵为正整数,故
∴有三种进货方案,
方案一:购进甲商品件,乙商品件;
方案二:购进甲商品件,乙商品件;
方案三:购进甲商品件,乙商品件.
【6-1】为了美化环境,张老师组织班级部分同学在操场植树,班级购买了若干树苗,若每人植棵,还剩棵,若每人植棵,最后一人有树植,但不足棵,这批树苗共有多少棵?
解:设共有人参与植树,则这批树苗共有棵,依题意得:
解得:.
又为正整数,
,
. 答:这批树苗共有棵.
【6-2】甲以5千米/时的速度进行有氧体育锻炼,2小时后,乙骑自行车从同一地出发沿同一条路追赶甲,根据他们两人的约定,乙最快不早于1小时追上甲,最慢不晚于1小时15分追上甲.那么乙骑车的速度应当控制在什么范围
解:设乙骑车的速度为x千米/时,依题意得
解这个不等式组,得13≤x≤15
答:乙骑车的速度应控制在13~15千米/时这个范围内.
【6-3】为了美化环境,园林部门决定利用现有的3490盆甲种花卉和2950盆乙种花卉搭配A、B两种园艺造型共50个摆放在迎宾大道两侧,已知搭配一个A种造型需甲种花卉80盆,乙种花卉40盆,搭配一个B种造型需甲种花卉50盆,乙种花卉90盆.
(1)某校七年级(1)班课外活动小组承接了这个园艺造型搭配方案的设计,问符合题意的搭配方案有几种 请你帮助设计出来.
(2)若搭配一个A种造型的成本是800元,搭配一个B种造型的成本是960元,试说明(1)中哪种方案成本最低 最低成本是多少元
解: (1) 设搭配A种造型x个,则B种造型为(50-x)个,依题意得
解这个不等式组得31≤x≤33
∵x是整数,
∴x可取31、32、 33
∴可设计三种搭配方案:
①A种园艺造型31个,B种园艺造型19个;
②A种园艺造型32个,B种园艺造型18个;
③A种园艺造型33个,B种园艺造型17个.
(2) 方案①需成本: 31×800+ 19×960=43040(元);
方案②需成本: 32×800+ 18×960=42880(元) ;
方案③需成本: 33×800+ 17×960=42720(元).
应选择方案③,成本最低,最低成本为42720元.
(2)若搭配一个A种造型的成本是800元,搭配一个B种造型的成本是960元,试说明(1)中哪种方案成本最低 最低成本是多少元
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
