沪教版八年级数学上册试题 第18章《 正比例函数和反比例函数》单元综合复习题(含解析)
文档属性
| 名称 | 沪教版八年级数学上册试题 第18章《 正比例函数和反比例函数》单元综合复习题(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-25 20:31:47 | ||
图片预览




文档简介
第18章《 正比例函数和反比例函数》单元综合复习题
一、单选题
1.正比例函数,,的共同特点是( )
A.图象经过相同的象限 B.y随x的增大而减小
C.y随x的增大而增大 D.图象都经过原点
2.已知函数,若函数值,则自变量取值为( )
A. B. C.或 D.
3.对于函数(k是常数,),下列说法不正确的是( )
A.该函数是正比例函数 B.该函数图象过
C.该函数图象经过二、四象限 D.y随着x的增大而增大
4.已知的底边上的高为8cm,当底边从16 cm变化到5 cm时,的面积 ( )
A.从20 cm2变化到64 cm2 B.从40 cm2变化到128 cm2
C.从128 cm2变化到40 cm2 D.从64 cm2变化到20 cm2
5.无论a取什么实数,点都在直线l上,若是直线l上的点,那么的值是( )
A.0 B.1 C.4 D.9
6.如图,点为反比例函数(,)上的一点,点为轴负半轴上一点,连接,将线段绕点逆时针旋转,点的对应点为点.若点恰好也在反比例函数的图像上,且点的横坐标是点横坐标的两倍,则的值为( )
A. B. C. D.
7.已知函数(k为常数且),函数的图象和函数的图象关于直线对称.则下列判断正确的是( )
①函数的图象上的点的横坐标不可能等于2.
②若当时,x的取值范围为或.
A.①②都正确 B.①正确,②错误
C.①错误,②正确 D.①②都错误
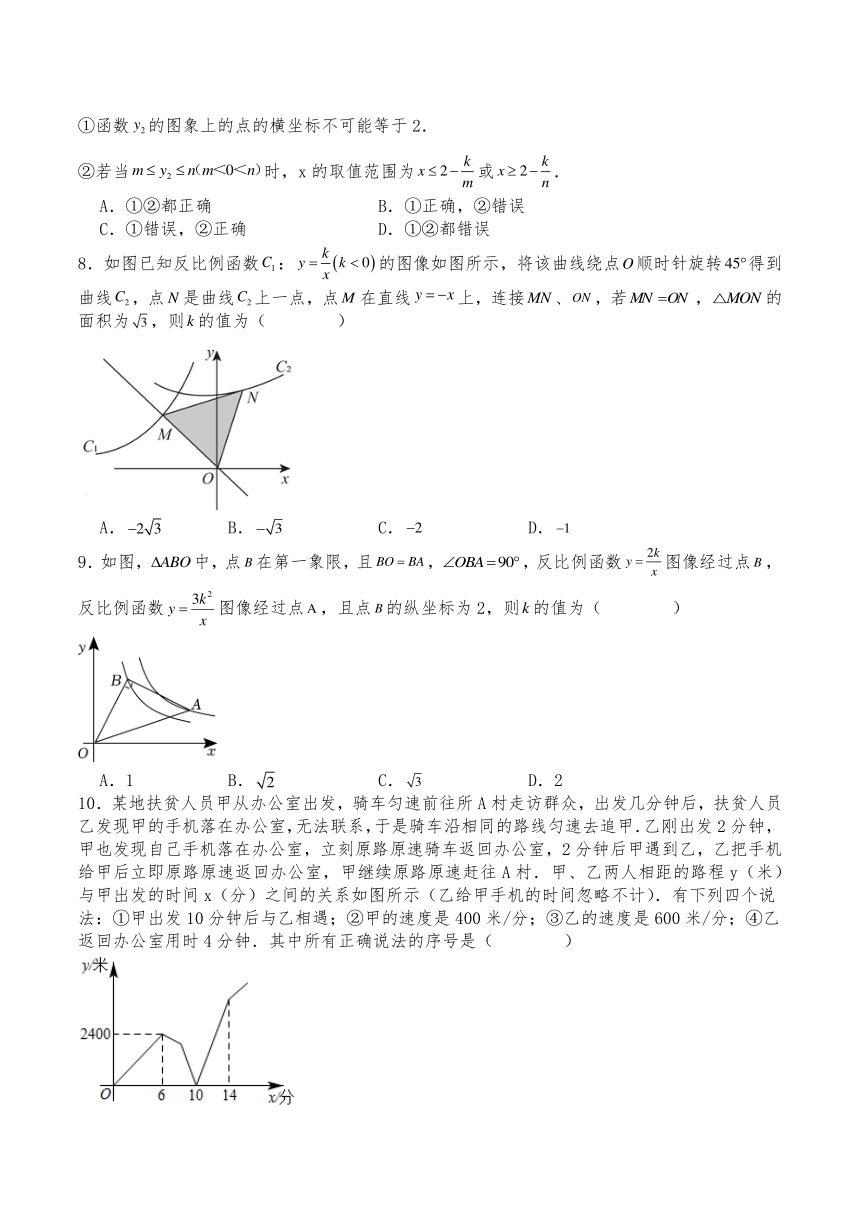
8.如图已知反比例函数:的图像如图所示,将该曲线绕点顺时针旋转得到曲线,点是曲线上一点,点在直线上,连接、,若,的面积为,则的值为( )
A. B. C. D.
9.如图,中,点在第一象限,且,,反比例函数图像经过点,反比例函数图像经过点,且点的纵坐标为2,则的值为( )
A.1 B. C. D.2
10.某地扶贫人员甲从办公室出发,骑车匀速前往所A村走访群众,出发几分钟后,扶贫人员乙发现甲的手机落在办公室,无法联系,于是骑车沿相同的路线匀速去追甲.乙刚出发2分钟,甲也发现自己手机落在办公室,立刻原路原速骑车返回办公室,2分钟后甲遇到乙,乙把手机给甲后立即原路原速返回办公室,甲继续原路原速赶往A村.甲、乙两人相距的路程y(米)与甲出发的时间x(分)之间的关系如图所示(乙给甲手机的时间忽略不计).有下列四个说法:①甲出发10分钟后与乙相遇;②甲的速度是400米/分;③乙的速度是600米/分;④乙返回办公室用时4分钟.其中所有正确说法的序号是( )
A.①②③④ B.②③④ C.①②④ D.②④
二、填空题
11.如果,那么 .
12.如图,点的坐标是,点的坐标是,为的中点,将绕点逆时针旋转后得到.若反比例函数的图象恰好经过的中点D,则k的值是 .
13.如图,在平面直角坐标系中,等边三角形的一条边轴于点B,经过点A的反比例函数(,)的图象交于点D,连结,,若点D是中点,的面积为3,则k的值为 .
14.如图,甲、乙两辆摩托车从相距的A,B两地同时相向而行,分别表示甲、乙两辆摩托车离A地的距离与行驶时问之间的函数关系.下列结论正确的是 .(写出所有正确结论的序号)
①乙摩托车行驶的速度是;
②当时,甲车的行驶路程超过;
③当时,甲摩托车离A地的距离小于乙摩托车离A地的距离;
④甲、乙两车相距不超过时,.
15.设p,q都是实数,且.我们规定:满足不等式的实数的所有取值的全体叫做闭区间,表示为.对于一个函数,如果它的自变量与函数值满足:当时,有,我们就称此函数是闭区间上的“闭函数”.请写出一个闭区间上的“闭函数”: .
16. 如图,直线l1⊥x轴于点(1,0),直线l2⊥x轴于点(2,0),直线l3⊥x轴于点(3,0),…,直线ln⊥x轴于点(n,0).函数y=x的图象与直线l1,l2,l3,…,ln分别交于点A1,A2,A3,…,An;函数y=2x的图象与直线l1,l2,l3,…,ln分别交于点B1,B2,B3,…,Bn.如果△OA1B1的面积记作S1,四边形A1A2B2B1的面积记作S2,四边形A2A3B3B2的面积记作S3,…,四边形An-1AnBnBn-1的面积记作Sn,那么S2019= .
17.在直角坐标系中,O是坐标原点,点P(m,n)在反比例函数的图象上.
(1)若m=k,n=k﹣2,则k= ;
(2)若m+n=k,OP=2,且此反比例函数,满足:当x>0时,y随x的增大而减小,则k= .
18.函数的图像如图所示,下列对该函数性质的论断正确的是
(1)该函数的图像是中心对称图形;
(2)当时,该函数在时取得最小值2;
(3)在每个象限内,的值随值的增大而减小;
(4)的值不可能为1.
三、解答题
19.如图,正方形分割成两个小正方形和两个长方形.
(1)若正方形边长为,正方形的面积是正方形的一半,求正方形的边的长.
(2)若正方形面积为,设,四边形的面积为,求y关于的函数解析式,并写出定义域.
(3)四边形的面积是否能够等于正方形面积的一半,如果能,请求出长,如果不能请说明理由.
20.媒体报道,近期“手足口病”可能进入发病高峰期,某校根据《学校卫生工作条例》,为预防“手足口病”,对教室进行“薰药消毒”.已知药物在燃烧及释放过程中,室内空气中每立方米含药量y(毫克)与燃烧时间x(分钟)之间的关系如图所
示(即图中线段OA和双曲线在A点及其右侧的部分),根据图象所示信息,解答下列问题:
(1)写出从药物释放开始,y与x之间的函数关系式及自变量的取值范围;
(2)据测定,当空气中每立方米的含药量低于2毫克时,对人体无毒害作用,那么从消毒开始,至少在多长时间内,师生不能进入教室?
21.如图,正方形OAPB、ADFE的顶点A、D、B在坐标轴上,点E在AP上,点P、F在函数上,已知正方形OAPB的面积是9.
(1)求k的值和直线OP的解析式;
(2)求正方形ADFE的边长
(3)函数在第三象限的图像上是否存在一点Q,使得△ABQ的面积为10.5?若存在,求出Q点坐标;若不存在,请说明理由.
22.某种原料需要达到及以上才能加工制作零件,如图表示原料的温度与时间之间的关系,其中线段表示原料加热阶段:线段轴,表示原料的恒温阶段;曲线是双曲线的一部分.表示原料的降温阶段.根据图象回答下列问题:
(1)填空:的值为______;
(2)求线段对应的函数解析式;
(3)在图中所示的温度变化过程中,求可进行零件加工的时间长度.
23.如图,在平面直角坐标系中,双曲线经过、两点,为直角三角形,轴,轴,,.
(1)求反比例函数的表达式及点的坐标;
(2)点是轴正半轴上的动点,连接、;
①求的最小值;
②点是反比例函数的图象上的一个点,若是以为直角边的等腰直角三角形时,求所有满足条件的点的坐标.
24.小刚和小聪同住一个小区,商量周日去体育场看一场足球赛.周日下午,小刚先出发去体育场,走了一段路后,在途中停下去便利店买水,后来发现球赛的时间快到了,就加快脚步走向体育场:小聪因家中有事迟出发,离家后跑步去体育场,如图所示:他们从家到体育场所走的路程S(米)与小刚离家时间t(分钟)之间的对应关系,根据图象回答下列问题:
(1)小刚家到体育场的路程是_________米,小聪比小刚早到体育场_________分钟;
(2)小刚出发几分钟后,小聪追上了小刚?
(3)体育场的球赛是下午,小刚在便利店买完水后如果还按原来走路的速度到体育场,是否会迟到?若迟到,请计算出迟到几分钟?若没迟到,请说明理由.
25.我们研究反比例函数图象平移后的性质.
初步探究
(1)将反比例函数的图象向左平移一个单位,可以得到函数的图象(如图①),观察图象,判断以下结论是否正确(正确的打“”,错误的打“”):
①该函数图象与y轴的交点坐标是;(_________)
②该函数图象是中心对称图形,对称中心是;(_________)
③当时,y随x的增大而减小;(_________)
(2)在图②中画出函数的图象,根据图象回答下列问题:
①该函数图象是中心对称图形,对称中心是(________,________)
②当时,则y的范围是______________;
③当时,则x的范围是______________;
问题解决
(3)若函数的图象可以由函数的图象通过平移得到,求m的值;
深入思考
(4)对于任意正数k,方程均无解,直接写出b,k满足的数量关系.
答案
一、单选题
1.D
【分析】根据正比例函数的性质即可求解.正比例函数y=kx的图象是经过原点的一条直线;K>0时,图像经过第一、三象限,y随x的增大而减小;K<0时,图像经过第二、四象限,y随x的增大而增大.
【解析】解:因为,所以的图象经过第一、三象限,y随x的增大而增大.
因为,,所以,的图象均经过第二、四象限,y随x的增大而减小.
故A项、B项、C项均不符合题意;因为三个函数均是正比例函数,所以三个函数的图象都是经过原点的直线,故D项符合题意.
故选D.
2.B
【分析】将分别代入y=2x+1和y=4x中,即可求出的值,结合x的取值范围即可得解.
【解析】解:当时,,
解得:
∵
所以不合题意,舍去;
当时,,
解得:,符合题意,
当函数值时,自变量取值为.
故选:B.
3.D
【分析】由正比例函数定义可判断A,代入点(,k)可判断B,由(k是常数,),是负数可判断C和D.
【解析】A.该函数符合正比例函数定义,故该选项正确,不符合题意;;
B.当,故该选项正确,不符合题意;
C. 由(k是常数,),是负数,则该函数图象经过二、四象限,故该选项正确,不符合题意;
D. y随着x的增大而减小,故该选项不正确,符合题意;
故选D
4.D
【分析】根据(底高)计算分别计算得出最值即可.
【解析】解:当的底边上的高为cm,底边cm时,
cm2;
底边cm时,cm2.
故选:D.
5.B
【分析】根据题意可得出直线l的解析式为y=2x,由Q(m,n)是直线l上的点,利用一次函数图象上点的坐标特征可得出n=2m,再将其代入(2m﹣n﹣1)2中即可求出结论.
【解析】解:∵无论a取什么实数,点P(a+1,2a+2)都在直线l上,且2a+2=2(a+1),
∴直线l的解析式为y=2x.
又∵Q(m,n)是直线l上的点,
∴n=2m,
∴(2m﹣n﹣1)2=(2m﹣2m﹣1)2=1.
故选:B.
6.B
【分析】首先可证得,得出,,再得出点的横坐标,进而得出点的纵坐标,再利用,求出点B的纵坐标,进而得出点的横坐标,最后根据,建立方程求解即可得出结论.
【解析】解:如图,过点作轴于点,过点作轴于点,
,
,
由旋转知,,,
,
,
,
,,
点的横坐标是点横坐标的两倍,且点,
点,
点在反比例函数的图象上,
,
,
,,
,
,
点在反比例函数的图象上,
,
,
,
,
,
,
故选:B.
7.B
【分析】先根据反比例函数的性质、轴对称的性质、函数图象的平移画出图形并得到;①根据解析式即可判断①;②根据反比例函数的增减性结合函数图象即可解答.
【解析】解:如图:由函数,根据函数的图象和函数的图象关于直线对称可知
∵,即,
∴函数的图象上的点的横坐标不可能等于2说法正确,即①正确;
当时,
当时,则,可得:
∵,,
∴,
当时,则,可得:
∵,,
∴,
综上,当时,x的取值范围为且,即②错误.
故选B.
8.B
【分析】将直线和曲线绕点O逆时针旋转,则直线与x轴重合,曲线与曲线重合,即可求解.
【解析】解:∵将直线和曲线绕点O逆时针旋转,
则直线与x轴重合,曲线与曲线重合,
∴旋转后点N落在曲线上,点M落在x轴上,如图所示,
设点M,N的对应点分别是,
过点作轴于点P,连接.
,
,
∴,
∴(舍)或,
故选B.
9.A
【分析】如图:作轴于,轴于,则直线与直线交于点,在确定点B的坐标,进而确定BE、OE的长,再证明得到、,则可确定A点坐标,然后将A点坐标代入求出k,最后再根据函数图像所在的象限解答即可.
【解析】解:如图,作轴于,轴于,则直线与直线交于点,
反比例函数图像经过点,点的纵坐标为2,
点,
,,
,
,
,
,
在和中
,
,,
,
,
反比例函数图像经过点,
,
解得,
反比例函数图像在第一象限,
,
.
故选:A.
10.A
【分析】由图可知甲出发分钟后,甲乙距离为,即可判断①,根据时,,即可判断②,根据第4个拐点,乙返回办公室,判断④,根据函数图象第一个拐点的意义是,乙出发,第二个拐点的意义为:甲返回,继而得出③.
【解析】由图可知甲出发分钟后,甲乙距离为,故甲出发十分钟后与乙相遇,①正确;
甲的速度:(米/分),故②正确;
根据函数图象可知,乙返回办公室用了(分钟),故④正确;
依题意,函数图象第一个拐点的意义是,乙出发;第二个拐点的意义为:2分钟后,甲返回,
∵甲的速度:(米/分)
∴乙的速度:(米/分),故③正确
故选:A.
二、填空题
11.
【分析】将代入计算即可得.
【解析】解:,
,
故答案为:.
12.15
【解析】解:作轴于.
,
,,
,
在中,
,
,
,,
点的坐标是,点的坐标是,
,,
,,
,
,
,
∴D(3,5)
反比例函数的图象经过点,
.
故答案为:15.
13.
【分析】利用反比例函数的几何意义,表示出点A的坐标的关系,利用的面积,求出点A的坐标的积,从而求出答案.
【解析】解:如下图,过C作、轴,作轴,
设点,
∴,,
∵为等边三角形且,
∴,,
∴矩形中,,
∵D是中点,
∴DE=14b,
∵,
∴,
∴,
∴,
∴,
∵,
∴,
∴,
∴,
∴,
∴,
故答案为:.
14.①②④
【分析】先求出甲乙的速度,再逐项分析即可.
【解析】由图可得,甲摩托车行驶的速度是,
乙摩托车行驶的速度是,故①正确;
当时,甲车的行驶路程超过,故②正确;
当时,甲摩托车离A地的距离,乙摩托车离A地的距离,即甲摩托车离A地的距离等于乙摩托车离A地的距离;
由图可得,当时,甲摩托车离A地的距离大于乙摩托车离A地的距离;故③错误;
设小时时甲、乙两车相距为,则,解得或,
故甲、乙两车相距不超过时,,故④正确;
综上,结论正确的是①②④;
故答案为:①②④.
15.
【分析】根据闭函数与反比例函数的特点即可求解.
【解析】由函数的图像可知,当时,函数值y随着自变量x的增大而减少,
而当时, ; 时, ,故也有,
所以函数是闭区间上的“闭函数”,
故答案为:.
16.
【分析】先结合图形确定的长度规律及图形形状为梯形的规律,再根据所得规律将具体值代入梯形面积公式即得.
【解析】解:由题意可得:当时,,
∴
∴,
∵直线l1⊥x轴,直线l2⊥x轴,直线l3⊥x轴,,直线ln⊥x轴
∴l1∥l2∥l3∥∥ln
∴当时四边形An-1AnBnBn-1是梯形
∵平行线间距离处处相等,所以梯形An-1AnBnBn-1的高为1
∴
∴
故答案为:.
17. 3 1+
【分析】(1)函数经过一定点,将此点坐标代入函数解析式(k≠0),即可求得k的值;
(2)根据点(x,y)到原点的距离公式d=,得到关于m,n的方程;
再结合完全平方公式的变形,得到关于k的方程,进一步求得k值.
【解析】解:(1)根据题意,得
k﹣2==1,
∴k=3.
(2)∵点P(m,n)在反比例函数y=的图象上.
∴mn=k
又∵OP=2,
∴=2,
∴(m+n)2﹣2mn﹣4=0,
又m+n=k,mn=k,
得k2﹣2k=4,
(k﹣1)2=5,
∵x>0时,y随x的增大而减小,则k>0.
∴k﹣1=,
k=1+.
18.(1)(2)(4)
【分析】根据中心对称图形的特征判断论断(1);结合函数图像判断论断(2)(3)(4).
【解析】解:(1)由图像可以看出函数图像上的每一个点都可以找到关于原点对称的点,故正确;
(2)结合图像的2个分支可以看出,在第一象限内,最低点的坐标为,故正确;
(3)在每个象限内,不同自变量的取值,函数值的变化是不同的,故错误;
(4)在第一象限y的最小值为2,在第三象限最大值为,故不可能为1,故正确.
∴正确的有(1)(2)(4).
故答案为(1)(2)(4).
三、解答题
19.(1)解:设,
∵正方形边长为,正方形分割成两个小正方形、和两个长方形、,
∴,
根据题意列方程得:,
解得:,(不合题意,舍去),
∴的长是.
(2)∵正方形面积为,
∴,
设,则,
∴,
整理得:,
∴y关于的函数解析式为.
(3)根据题意可知:,
∴,
整理得:,
解得:,(不合题意,舍去),
∴当的长为时,四边形的面积能够等于正方形面积的一半.
20.(1)根据题意,药物释放过程中,室内每立方米空气中的含药量y(毫克)与时间x(分钟)发反比例,
把点(25,6)代入y=得k=25×6=150,
∴y=(x≥15),
(2)把y=2代入y=,
解得x=75,
∴从消毒开始,师生至少在75分钟内不能进入教室.
21.(1)∵正方形OAPB的面积为9,
∴PA=PB=3,
∴P点坐标为(3,3),
把P(3,3)代入得,k=3×3=9,
即;
设直线OP的解析式为y=k1x,
把P(3,3)代入y=k1x得,k1=1,
∴直线OP的解析式为y=x;
(2)设正方形ADFE的边长为a,则F点的坐标为(a+3,a),
把F(a+3,a)代入得,a(a+3)=9,解得a1=,a2=,
∴正方形ADFE的边长为得;
(3)∵P(3,3)且四边形AOBP是正方形,
∴AO=BO=3,
设Q(x,)(x<0),连接QO,QB,QA,AB,如图所示,
假定△ABQ的面积为10.5,则有,
S△BOQ+S△AOQ+S△AOB=10.5
即,
∵x<0
∴方程整理得,
∵△=
∴此方程无实数解,
故函数在第三象限的图像上不存在一点Q,使得△ABQ的面积为10.5
22.(1)解:∵线段轴,且点的纵坐标为100,
∴,解得,
故答案为:21;
(2)解:设线段的解析式为,
把代入得,,
解得,
∴线段的解析式为;
(3)解:当时,,
解得,
当时,,
解得,
∴,
∴在图中所示的温度变化过程中,可进行零件加工的时间长度为.
23.(1)解:,,
,
将代入得:
,
解得,
反比例函数的表达式为,
在中,令得,
的坐标为;
(2)作关于轴的对称点,连接交轴于,此时最小,如图:
,关于轴对称,
,
当,,共线时,最小,即最小,最小值为的长度,
由(1)知,,
,
,
的最小值是;
设,,
当为直角顶点时,过作轴,过作于,过作于,如图:
的等腰直角三角形,
,,
,
≌,
,,
,
解得,
;
当为直角顶点时,过作轴于,过作于,如图:
同理可得,,
,
解得或舍去,
;
综上所述,的坐标为或.
24.(1)解:由图可知:
小刚家到体育场的路程是1200米,
(分钟),
即小聪比小刚早到体育场6分钟,
故答案为:1200,6;
(2)解:小聪的速度:,
,
,
答:小刚出发分钟后,小聪追上了小刚;
(3)解:小刚原来步行速度:,
,
∴小刚到达体育场所用时间:
,
即小刚出门25分钟后球赛开始,
∵,
∴不会迟到.
25.(1)解:①观察图可得,该函数图象与y轴的交点坐标是,故①;
②根据函数图象可知,该函数图象是中心对称图形,对称中心是,故②;
③当时,y随x的增大而减小,当,y随x的增大而减小,但,故③;
故答案为:①;②;③;
(2)解:函数图象,如图所示:
① 该函数图象是中心对称图形,对称中心是;
② 根据函数图象可知,当时,则y的范围是;
③ 根据函数图象可知,当时,则x的范围是或;
故答案为:①;②;③或.
(3)解:,
∵函数的图象可以由函数的图象通过平移得到,
∴,
解得.
(4)解:,
,
,
∵对于任意k,方程均无解,当时分式无意义,
∴.
一、单选题
1.正比例函数,,的共同特点是( )
A.图象经过相同的象限 B.y随x的增大而减小
C.y随x的增大而增大 D.图象都经过原点
2.已知函数,若函数值,则自变量取值为( )
A. B. C.或 D.
3.对于函数(k是常数,),下列说法不正确的是( )
A.该函数是正比例函数 B.该函数图象过
C.该函数图象经过二、四象限 D.y随着x的增大而增大
4.已知的底边上的高为8cm,当底边从16 cm变化到5 cm时,的面积 ( )
A.从20 cm2变化到64 cm2 B.从40 cm2变化到128 cm2
C.从128 cm2变化到40 cm2 D.从64 cm2变化到20 cm2
5.无论a取什么实数,点都在直线l上,若是直线l上的点,那么的值是( )
A.0 B.1 C.4 D.9
6.如图,点为反比例函数(,)上的一点,点为轴负半轴上一点,连接,将线段绕点逆时针旋转,点的对应点为点.若点恰好也在反比例函数的图像上,且点的横坐标是点横坐标的两倍,则的值为( )
A. B. C. D.
7.已知函数(k为常数且),函数的图象和函数的图象关于直线对称.则下列判断正确的是( )
①函数的图象上的点的横坐标不可能等于2.
②若当时,x的取值范围为或.
A.①②都正确 B.①正确,②错误
C.①错误,②正确 D.①②都错误
8.如图已知反比例函数:的图像如图所示,将该曲线绕点顺时针旋转得到曲线,点是曲线上一点,点在直线上,连接、,若,的面积为,则的值为( )
A. B. C. D.
9.如图,中,点在第一象限,且,,反比例函数图像经过点,反比例函数图像经过点,且点的纵坐标为2,则的值为( )
A.1 B. C. D.2
10.某地扶贫人员甲从办公室出发,骑车匀速前往所A村走访群众,出发几分钟后,扶贫人员乙发现甲的手机落在办公室,无法联系,于是骑车沿相同的路线匀速去追甲.乙刚出发2分钟,甲也发现自己手机落在办公室,立刻原路原速骑车返回办公室,2分钟后甲遇到乙,乙把手机给甲后立即原路原速返回办公室,甲继续原路原速赶往A村.甲、乙两人相距的路程y(米)与甲出发的时间x(分)之间的关系如图所示(乙给甲手机的时间忽略不计).有下列四个说法:①甲出发10分钟后与乙相遇;②甲的速度是400米/分;③乙的速度是600米/分;④乙返回办公室用时4分钟.其中所有正确说法的序号是( )
A.①②③④ B.②③④ C.①②④ D.②④
二、填空题
11.如果,那么 .
12.如图,点的坐标是,点的坐标是,为的中点,将绕点逆时针旋转后得到.若反比例函数的图象恰好经过的中点D,则k的值是 .
13.如图,在平面直角坐标系中,等边三角形的一条边轴于点B,经过点A的反比例函数(,)的图象交于点D,连结,,若点D是中点,的面积为3,则k的值为 .
14.如图,甲、乙两辆摩托车从相距的A,B两地同时相向而行,分别表示甲、乙两辆摩托车离A地的距离与行驶时问之间的函数关系.下列结论正确的是 .(写出所有正确结论的序号)
①乙摩托车行驶的速度是;
②当时,甲车的行驶路程超过;
③当时,甲摩托车离A地的距离小于乙摩托车离A地的距离;
④甲、乙两车相距不超过时,.
15.设p,q都是实数,且.我们规定:满足不等式的实数的所有取值的全体叫做闭区间,表示为.对于一个函数,如果它的自变量与函数值满足:当时,有,我们就称此函数是闭区间上的“闭函数”.请写出一个闭区间上的“闭函数”: .
16. 如图,直线l1⊥x轴于点(1,0),直线l2⊥x轴于点(2,0),直线l3⊥x轴于点(3,0),…,直线ln⊥x轴于点(n,0).函数y=x的图象与直线l1,l2,l3,…,ln分别交于点A1,A2,A3,…,An;函数y=2x的图象与直线l1,l2,l3,…,ln分别交于点B1,B2,B3,…,Bn.如果△OA1B1的面积记作S1,四边形A1A2B2B1的面积记作S2,四边形A2A3B3B2的面积记作S3,…,四边形An-1AnBnBn-1的面积记作Sn,那么S2019= .
17.在直角坐标系中,O是坐标原点,点P(m,n)在反比例函数的图象上.
(1)若m=k,n=k﹣2,则k= ;
(2)若m+n=k,OP=2,且此反比例函数,满足:当x>0时,y随x的增大而减小,则k= .
18.函数的图像如图所示,下列对该函数性质的论断正确的是
(1)该函数的图像是中心对称图形;
(2)当时,该函数在时取得最小值2;
(3)在每个象限内,的值随值的增大而减小;
(4)的值不可能为1.
三、解答题
19.如图,正方形分割成两个小正方形和两个长方形.
(1)若正方形边长为,正方形的面积是正方形的一半,求正方形的边的长.
(2)若正方形面积为,设,四边形的面积为,求y关于的函数解析式,并写出定义域.
(3)四边形的面积是否能够等于正方形面积的一半,如果能,请求出长,如果不能请说明理由.
20.媒体报道,近期“手足口病”可能进入发病高峰期,某校根据《学校卫生工作条例》,为预防“手足口病”,对教室进行“薰药消毒”.已知药物在燃烧及释放过程中,室内空气中每立方米含药量y(毫克)与燃烧时间x(分钟)之间的关系如图所
示(即图中线段OA和双曲线在A点及其右侧的部分),根据图象所示信息,解答下列问题:
(1)写出从药物释放开始,y与x之间的函数关系式及自变量的取值范围;
(2)据测定,当空气中每立方米的含药量低于2毫克时,对人体无毒害作用,那么从消毒开始,至少在多长时间内,师生不能进入教室?
21.如图,正方形OAPB、ADFE的顶点A、D、B在坐标轴上,点E在AP上,点P、F在函数上,已知正方形OAPB的面积是9.
(1)求k的值和直线OP的解析式;
(2)求正方形ADFE的边长
(3)函数在第三象限的图像上是否存在一点Q,使得△ABQ的面积为10.5?若存在,求出Q点坐标;若不存在,请说明理由.
22.某种原料需要达到及以上才能加工制作零件,如图表示原料的温度与时间之间的关系,其中线段表示原料加热阶段:线段轴,表示原料的恒温阶段;曲线是双曲线的一部分.表示原料的降温阶段.根据图象回答下列问题:
(1)填空:的值为______;
(2)求线段对应的函数解析式;
(3)在图中所示的温度变化过程中,求可进行零件加工的时间长度.
23.如图,在平面直角坐标系中,双曲线经过、两点,为直角三角形,轴,轴,,.
(1)求反比例函数的表达式及点的坐标;
(2)点是轴正半轴上的动点,连接、;
①求的最小值;
②点是反比例函数的图象上的一个点,若是以为直角边的等腰直角三角形时,求所有满足条件的点的坐标.
24.小刚和小聪同住一个小区,商量周日去体育场看一场足球赛.周日下午,小刚先出发去体育场,走了一段路后,在途中停下去便利店买水,后来发现球赛的时间快到了,就加快脚步走向体育场:小聪因家中有事迟出发,离家后跑步去体育场,如图所示:他们从家到体育场所走的路程S(米)与小刚离家时间t(分钟)之间的对应关系,根据图象回答下列问题:
(1)小刚家到体育场的路程是_________米,小聪比小刚早到体育场_________分钟;
(2)小刚出发几分钟后,小聪追上了小刚?
(3)体育场的球赛是下午,小刚在便利店买完水后如果还按原来走路的速度到体育场,是否会迟到?若迟到,请计算出迟到几分钟?若没迟到,请说明理由.
25.我们研究反比例函数图象平移后的性质.
初步探究
(1)将反比例函数的图象向左平移一个单位,可以得到函数的图象(如图①),观察图象,判断以下结论是否正确(正确的打“”,错误的打“”):
①该函数图象与y轴的交点坐标是;(_________)
②该函数图象是中心对称图形,对称中心是;(_________)
③当时,y随x的增大而减小;(_________)
(2)在图②中画出函数的图象,根据图象回答下列问题:
①该函数图象是中心对称图形,对称中心是(________,________)
②当时,则y的范围是______________;
③当时,则x的范围是______________;
问题解决
(3)若函数的图象可以由函数的图象通过平移得到,求m的值;
深入思考
(4)对于任意正数k,方程均无解,直接写出b,k满足的数量关系.
答案
一、单选题
1.D
【分析】根据正比例函数的性质即可求解.正比例函数y=kx的图象是经过原点的一条直线;K>0时,图像经过第一、三象限,y随x的增大而减小;K<0时,图像经过第二、四象限,y随x的增大而增大.
【解析】解:因为,所以的图象经过第一、三象限,y随x的增大而增大.
因为,,所以,的图象均经过第二、四象限,y随x的增大而减小.
故A项、B项、C项均不符合题意;因为三个函数均是正比例函数,所以三个函数的图象都是经过原点的直线,故D项符合题意.
故选D.
2.B
【分析】将分别代入y=2x+1和y=4x中,即可求出的值,结合x的取值范围即可得解.
【解析】解:当时,,
解得:
∵
所以不合题意,舍去;
当时,,
解得:,符合题意,
当函数值时,自变量取值为.
故选:B.
3.D
【分析】由正比例函数定义可判断A,代入点(,k)可判断B,由(k是常数,),是负数可判断C和D.
【解析】A.该函数符合正比例函数定义,故该选项正确,不符合题意;;
B.当,故该选项正确,不符合题意;
C. 由(k是常数,),是负数,则该函数图象经过二、四象限,故该选项正确,不符合题意;
D. y随着x的增大而减小,故该选项不正确,符合题意;
故选D
4.D
【分析】根据(底高)计算分别计算得出最值即可.
【解析】解:当的底边上的高为cm,底边cm时,
cm2;
底边cm时,cm2.
故选:D.
5.B
【分析】根据题意可得出直线l的解析式为y=2x,由Q(m,n)是直线l上的点,利用一次函数图象上点的坐标特征可得出n=2m,再将其代入(2m﹣n﹣1)2中即可求出结论.
【解析】解:∵无论a取什么实数,点P(a+1,2a+2)都在直线l上,且2a+2=2(a+1),
∴直线l的解析式为y=2x.
又∵Q(m,n)是直线l上的点,
∴n=2m,
∴(2m﹣n﹣1)2=(2m﹣2m﹣1)2=1.
故选:B.
6.B
【分析】首先可证得,得出,,再得出点的横坐标,进而得出点的纵坐标,再利用,求出点B的纵坐标,进而得出点的横坐标,最后根据,建立方程求解即可得出结论.
【解析】解:如图,过点作轴于点,过点作轴于点,
,
,
由旋转知,,,
,
,
,
,,
点的横坐标是点横坐标的两倍,且点,
点,
点在反比例函数的图象上,
,
,
,,
,
,
点在反比例函数的图象上,
,
,
,
,
,
,
故选:B.
7.B
【分析】先根据反比例函数的性质、轴对称的性质、函数图象的平移画出图形并得到;①根据解析式即可判断①;②根据反比例函数的增减性结合函数图象即可解答.
【解析】解:如图:由函数,根据函数的图象和函数的图象关于直线对称可知
∵,即,
∴函数的图象上的点的横坐标不可能等于2说法正确,即①正确;
当时,
当时,则,可得:
∵,,
∴,
当时,则,可得:
∵,,
∴,
综上,当时,x的取值范围为且,即②错误.
故选B.
8.B
【分析】将直线和曲线绕点O逆时针旋转,则直线与x轴重合,曲线与曲线重合,即可求解.
【解析】解:∵将直线和曲线绕点O逆时针旋转,
则直线与x轴重合,曲线与曲线重合,
∴旋转后点N落在曲线上,点M落在x轴上,如图所示,
设点M,N的对应点分别是,
过点作轴于点P,连接.
,
,
∴,
∴(舍)或,
故选B.
9.A
【分析】如图:作轴于,轴于,则直线与直线交于点,在确定点B的坐标,进而确定BE、OE的长,再证明得到、,则可确定A点坐标,然后将A点坐标代入求出k,最后再根据函数图像所在的象限解答即可.
【解析】解:如图,作轴于,轴于,则直线与直线交于点,
反比例函数图像经过点,点的纵坐标为2,
点,
,,
,
,
,
,
在和中
,
,,
,
,
反比例函数图像经过点,
,
解得,
反比例函数图像在第一象限,
,
.
故选:A.
10.A
【分析】由图可知甲出发分钟后,甲乙距离为,即可判断①,根据时,,即可判断②,根据第4个拐点,乙返回办公室,判断④,根据函数图象第一个拐点的意义是,乙出发,第二个拐点的意义为:甲返回,继而得出③.
【解析】由图可知甲出发分钟后,甲乙距离为,故甲出发十分钟后与乙相遇,①正确;
甲的速度:(米/分),故②正确;
根据函数图象可知,乙返回办公室用了(分钟),故④正确;
依题意,函数图象第一个拐点的意义是,乙出发;第二个拐点的意义为:2分钟后,甲返回,
∵甲的速度:(米/分)
∴乙的速度:(米/分),故③正确
故选:A.
二、填空题
11.
【分析】将代入计算即可得.
【解析】解:,
,
故答案为:.
12.15
【解析】解:作轴于.
,
,,
,
在中,
,
,
,,
点的坐标是,点的坐标是,
,,
,,
,
,
,
∴D(3,5)
反比例函数的图象经过点,
.
故答案为:15.
13.
【分析】利用反比例函数的几何意义,表示出点A的坐标的关系,利用的面积,求出点A的坐标的积,从而求出答案.
【解析】解:如下图,过C作、轴,作轴,
设点,
∴,,
∵为等边三角形且,
∴,,
∴矩形中,,
∵D是中点,
∴DE=14b,
∵,
∴,
∴,
∴,
∴,
∵,
∴,
∴,
∴,
∴,
∴,
故答案为:.
14.①②④
【分析】先求出甲乙的速度,再逐项分析即可.
【解析】由图可得,甲摩托车行驶的速度是,
乙摩托车行驶的速度是,故①正确;
当时,甲车的行驶路程超过,故②正确;
当时,甲摩托车离A地的距离,乙摩托车离A地的距离,即甲摩托车离A地的距离等于乙摩托车离A地的距离;
由图可得,当时,甲摩托车离A地的距离大于乙摩托车离A地的距离;故③错误;
设小时时甲、乙两车相距为,则,解得或,
故甲、乙两车相距不超过时,,故④正确;
综上,结论正确的是①②④;
故答案为:①②④.
15.
【分析】根据闭函数与反比例函数的特点即可求解.
【解析】由函数的图像可知,当时,函数值y随着自变量x的增大而减少,
而当时, ; 时, ,故也有,
所以函数是闭区间上的“闭函数”,
故答案为:.
16.
【分析】先结合图形确定的长度规律及图形形状为梯形的规律,再根据所得规律将具体值代入梯形面积公式即得.
【解析】解:由题意可得:当时,,
∴
∴,
∵直线l1⊥x轴,直线l2⊥x轴,直线l3⊥x轴,,直线ln⊥x轴
∴l1∥l2∥l3∥∥ln
∴当时四边形An-1AnBnBn-1是梯形
∵平行线间距离处处相等,所以梯形An-1AnBnBn-1的高为1
∴
∴
故答案为:.
17. 3 1+
【分析】(1)函数经过一定点,将此点坐标代入函数解析式(k≠0),即可求得k的值;
(2)根据点(x,y)到原点的距离公式d=,得到关于m,n的方程;
再结合完全平方公式的变形,得到关于k的方程,进一步求得k值.
【解析】解:(1)根据题意,得
k﹣2==1,
∴k=3.
(2)∵点P(m,n)在反比例函数y=的图象上.
∴mn=k
又∵OP=2,
∴=2,
∴(m+n)2﹣2mn﹣4=0,
又m+n=k,mn=k,
得k2﹣2k=4,
(k﹣1)2=5,
∵x>0时,y随x的增大而减小,则k>0.
∴k﹣1=,
k=1+.
18.(1)(2)(4)
【分析】根据中心对称图形的特征判断论断(1);结合函数图像判断论断(2)(3)(4).
【解析】解:(1)由图像可以看出函数图像上的每一个点都可以找到关于原点对称的点,故正确;
(2)结合图像的2个分支可以看出,在第一象限内,最低点的坐标为,故正确;
(3)在每个象限内,不同自变量的取值,函数值的变化是不同的,故错误;
(4)在第一象限y的最小值为2,在第三象限最大值为,故不可能为1,故正确.
∴正确的有(1)(2)(4).
故答案为(1)(2)(4).
三、解答题
19.(1)解:设,
∵正方形边长为,正方形分割成两个小正方形、和两个长方形、,
∴,
根据题意列方程得:,
解得:,(不合题意,舍去),
∴的长是.
(2)∵正方形面积为,
∴,
设,则,
∴,
整理得:,
∴y关于的函数解析式为.
(3)根据题意可知:,
∴,
整理得:,
解得:,(不合题意,舍去),
∴当的长为时,四边形的面积能够等于正方形面积的一半.
20.(1)根据题意,药物释放过程中,室内每立方米空气中的含药量y(毫克)与时间x(分钟)发反比例,
把点(25,6)代入y=得k=25×6=150,
∴y=(x≥15),
(2)把y=2代入y=,
解得x=75,
∴从消毒开始,师生至少在75分钟内不能进入教室.
21.(1)∵正方形OAPB的面积为9,
∴PA=PB=3,
∴P点坐标为(3,3),
把P(3,3)代入得,k=3×3=9,
即;
设直线OP的解析式为y=k1x,
把P(3,3)代入y=k1x得,k1=1,
∴直线OP的解析式为y=x;
(2)设正方形ADFE的边长为a,则F点的坐标为(a+3,a),
把F(a+3,a)代入得,a(a+3)=9,解得a1=,a2=,
∴正方形ADFE的边长为得;
(3)∵P(3,3)且四边形AOBP是正方形,
∴AO=BO=3,
设Q(x,)(x<0),连接QO,QB,QA,AB,如图所示,
假定△ABQ的面积为10.5,则有,
S△BOQ+S△AOQ+S△AOB=10.5
即,
∵x<0
∴方程整理得,
∵△=
∴此方程无实数解,
故函数在第三象限的图像上不存在一点Q,使得△ABQ的面积为10.5
22.(1)解:∵线段轴,且点的纵坐标为100,
∴,解得,
故答案为:21;
(2)解:设线段的解析式为,
把代入得,,
解得,
∴线段的解析式为;
(3)解:当时,,
解得,
当时,,
解得,
∴,
∴在图中所示的温度变化过程中,可进行零件加工的时间长度为.
23.(1)解:,,
,
将代入得:
,
解得,
反比例函数的表达式为,
在中,令得,
的坐标为;
(2)作关于轴的对称点,连接交轴于,此时最小,如图:
,关于轴对称,
,
当,,共线时,最小,即最小,最小值为的长度,
由(1)知,,
,
,
的最小值是;
设,,
当为直角顶点时,过作轴,过作于,过作于,如图:
的等腰直角三角形,
,,
,
≌,
,,
,
解得,
;
当为直角顶点时,过作轴于,过作于,如图:
同理可得,,
,
解得或舍去,
;
综上所述,的坐标为或.
24.(1)解:由图可知:
小刚家到体育场的路程是1200米,
(分钟),
即小聪比小刚早到体育场6分钟,
故答案为:1200,6;
(2)解:小聪的速度:,
,
,
答:小刚出发分钟后,小聪追上了小刚;
(3)解:小刚原来步行速度:,
,
∴小刚到达体育场所用时间:
,
即小刚出门25分钟后球赛开始,
∵,
∴不会迟到.
25.(1)解:①观察图可得,该函数图象与y轴的交点坐标是,故①;
②根据函数图象可知,该函数图象是中心对称图形,对称中心是,故②;
③当时,y随x的增大而减小,当,y随x的增大而减小,但,故③;
故答案为:①;②;③;
(2)解:函数图象,如图所示:
① 该函数图象是中心对称图形,对称中心是;
② 根据函数图象可知,当时,则y的范围是;
③ 根据函数图象可知,当时,则x的范围是或;
故答案为:①;②;③或.
(3)解:,
∵函数的图象可以由函数的图象通过平移得到,
∴,
解得.
(4)解:,
,
,
∵对于任意k,方程均无解,当时分式无意义,
∴.
