19.2.1 正比例函数 课件(共14张PPT) 2023-2024学年人教版八年级数学下册
文档属性
| 名称 | 19.2.1 正比例函数 课件(共14张PPT) 2023-2024学年人教版八年级数学下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 24.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-25 16:25:37 | ||
图片预览






文档简介
(共15张PPT)
人教版八年级下册第十九章《一次函数》
19.2.1 正比例函数
情境引入:
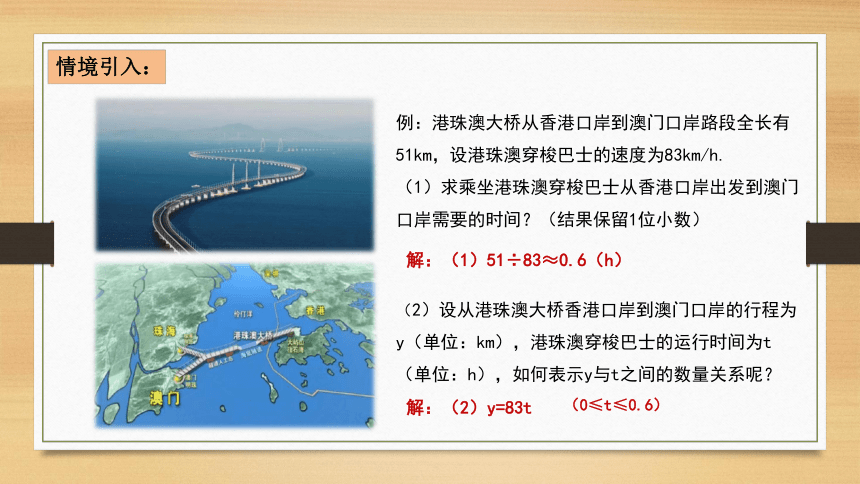
例:港珠澳大桥从香港口岸到澳门口岸路段全长有51km,设港珠澳穿梭巴士的速度为83km/h.
(1)求乘坐港珠澳穿梭巴士从香港口岸出发到澳门口岸需要的时间?(结果保留1位小数)
(2)设从港珠澳大桥香港口岸到澳门口岸的行程为y(单位:km),港珠澳穿梭巴士的运行时间为t(单位:h),如何表示y与t之间的数量关系呢?
解:(1)51÷83≈0.6(h)
解:(2)y=83t
(0≤t≤0.6)
探究1:正比例函数的定义
例1:自主完成下面练习题,先判断变量之间的对应关系是否是函数关系?如果是,请写出函数解析式
(1)圆的周长l随半径r的变化而变化.
(2)铁的密度是7.8g/cm3,铁块的质量m(单位:g)随它的体积V(单位:cm3)的变化而变化.
(3)每个练习本的厚度为0.5cm,一些练习本摞在一起的总厚度h(单位:cm)随练习本的本数n的变化而变化.
解:(3)h = 0.5 n
解:(1)l = 2πr
解:(2)m = 7.8 V
探究1:正比例函数的定义
定义:一般地,形如y=kx(k是常数,k≠0)的函数,叫做正比例函数,其中k叫做比例系数.
(1)l = 2π r
(2)m = 7.8 V
(3)h = 0.5 n
函数=常量×自变量
思考:观察三个函数解析式的结构,你能发现什么共同之处?
随堂检测:
1.下列式子,哪些表示y是x的正比例函数?如果是,请你指出比例系数k的值.
(1) (2) (3)
(4) 3-1 (5) 2( -)+2 (6)
是,k=
不是
不是
不是
是,k=2
是,k=
随堂检测:
2.若是 关于 的正比例函数,则 = .
3.已知与成正比例,且=1时,=-6,则当=-2时,= .
4.已知 关于+1 成正比例函数,当 =3时, =-9,求 与 的关系式 ?
12
解(1)∵ 关于+1 成正比例函数
∴ =k (+1 )
∵当 =3时, =-9
∴ =k(+1 )
∴k=
∴y= +1)
数缺形时少直观,形缺数时难入微
数形结合千般好,数形分家万事休
华罗庚
探究2:正比例函数的图像和性质
例2:画出下列正比例函数的图像.
(1); (2)
讨论:
1、正比例函数的图像有什么共同点?
2、正比例函数的图像与k值有何联系?
3、正比例函数中y如何随x的变化而变化的?
第一象限
第三象限
第二象限
第四象限
探究2:正比例函数的图像和性质
性质:一般地,正比例函数y=kx(k是常数,k≠0)的图像是一条经过原点的直线,我们称它为直线y=kx.当k>0时,直线 y=kx的图像经过一、三象限,从左向右上升, 即随着x增大,y也增大。当k<0时,直线y=kx的图像经过二、四象限,从左向右下降, 即随着x增大,y反而减小。
数形结合
随堂检测:
1.在下列图像中,表示函数y=kx(k<0)的图像是( )
2.函数y=4x的图象过第 象限, 经过点(0, )与点(1, ),y随x的增大而 .
3.设正比例函数y=mx的图像经过点A(m,4),且y的值随x值的增大而减小,则m= .
4. 若函数y=(m-1)是正比例函数,则该函数的图像经过第 象限.
x
y
0
A
x
y
0
B
x
y
0
C
x
y
0
D
c
一、三
0
4
增大
-2
二、四
随堂检测:
5.已知正比例函数y=(2m+4)x,求:
(1)当m为何值时,函数图像经过第一、三象限?
(2)当m为何值时,y随x的增大而减小?
(3)当m为何值时,点(1,3)在该函数图像上?
解(1)∵函数图像经过第一、三象限
∴2m+4>0
∴m>-2
(2)∵ y随x的增大而减小
∴2m+4<0
∴m<-2
(3)∵点(1,3)在该函数图像上
∴3=(2m+4)×1
∴m=
正比例函数
正比例函数:形如y=kx(k是常数,k≠0)
图像
总结归纳:
实际问题
归纳
观察
猜想
验证
正比例函数的性质
数形结合
特殊
一般
布置作业:
1.《巅峰对决》作业本p77
2.了解正比例函数的由来和发展史
f(x)=+sin(axπ)
将冰冷的美丽转化为火热的思考!
人教版八年级下册第十九章《一次函数》
19.2.1 正比例函数
情境引入:
例:港珠澳大桥从香港口岸到澳门口岸路段全长有51km,设港珠澳穿梭巴士的速度为83km/h.
(1)求乘坐港珠澳穿梭巴士从香港口岸出发到澳门口岸需要的时间?(结果保留1位小数)
(2)设从港珠澳大桥香港口岸到澳门口岸的行程为y(单位:km),港珠澳穿梭巴士的运行时间为t(单位:h),如何表示y与t之间的数量关系呢?
解:(1)51÷83≈0.6(h)
解:(2)y=83t
(0≤t≤0.6)
探究1:正比例函数的定义
例1:自主完成下面练习题,先判断变量之间的对应关系是否是函数关系?如果是,请写出函数解析式
(1)圆的周长l随半径r的变化而变化.
(2)铁的密度是7.8g/cm3,铁块的质量m(单位:g)随它的体积V(单位:cm3)的变化而变化.
(3)每个练习本的厚度为0.5cm,一些练习本摞在一起的总厚度h(单位:cm)随练习本的本数n的变化而变化.
解:(3)h = 0.5 n
解:(1)l = 2πr
解:(2)m = 7.8 V
探究1:正比例函数的定义
定义:一般地,形如y=kx(k是常数,k≠0)的函数,叫做正比例函数,其中k叫做比例系数.
(1)l = 2π r
(2)m = 7.8 V
(3)h = 0.5 n
函数=常量×自变量
思考:观察三个函数解析式的结构,你能发现什么共同之处?
随堂检测:
1.下列式子,哪些表示y是x的正比例函数?如果是,请你指出比例系数k的值.
(1) (2) (3)
(4) 3-1 (5) 2( -)+2 (6)
是,k=
不是
不是
不是
是,k=2
是,k=
随堂检测:
2.若是 关于 的正比例函数,则 = .
3.已知与成正比例,且=1时,=-6,则当=-2时,= .
4.已知 关于+1 成正比例函数,当 =3时, =-9,求 与 的关系式 ?
12
解(1)∵ 关于+1 成正比例函数
∴ =k (+1 )
∵当 =3时, =-9
∴ =k(+1 )
∴k=
∴y= +1)
数缺形时少直观,形缺数时难入微
数形结合千般好,数形分家万事休
华罗庚
探究2:正比例函数的图像和性质
例2:画出下列正比例函数的图像.
(1); (2)
讨论:
1、正比例函数的图像有什么共同点?
2、正比例函数的图像与k值有何联系?
3、正比例函数中y如何随x的变化而变化的?
第一象限
第三象限
第二象限
第四象限
探究2:正比例函数的图像和性质
性质:一般地,正比例函数y=kx(k是常数,k≠0)的图像是一条经过原点的直线,我们称它为直线y=kx.当k>0时,直线 y=kx的图像经过一、三象限,从左向右上升, 即随着x增大,y也增大。当k<0时,直线y=kx的图像经过二、四象限,从左向右下降, 即随着x增大,y反而减小。
数形结合
随堂检测:
1.在下列图像中,表示函数y=kx(k<0)的图像是( )
2.函数y=4x的图象过第 象限, 经过点(0, )与点(1, ),y随x的增大而 .
3.设正比例函数y=mx的图像经过点A(m,4),且y的值随x值的增大而减小,则m= .
4. 若函数y=(m-1)是正比例函数,则该函数的图像经过第 象限.
x
y
0
A
x
y
0
B
x
y
0
C
x
y
0
D
c
一、三
0
4
增大
-2
二、四
随堂检测:
5.已知正比例函数y=(2m+4)x,求:
(1)当m为何值时,函数图像经过第一、三象限?
(2)当m为何值时,y随x的增大而减小?
(3)当m为何值时,点(1,3)在该函数图像上?
解(1)∵函数图像经过第一、三象限
∴2m+4>0
∴m>-2
(2)∵ y随x的增大而减小
∴2m+4<0
∴m<-2
(3)∵点(1,3)在该函数图像上
∴3=(2m+4)×1
∴m=
正比例函数
正比例函数:形如y=kx(k是常数,k≠0)
图像
总结归纳:
实际问题
归纳
观察
猜想
验证
正比例函数的性质
数形结合
特殊
一般
布置作业:
1.《巅峰对决》作业本p77
2.了解正比例函数的由来和发展史
f(x)=+sin(axπ)
将冰冷的美丽转化为火热的思考!
