第十章 概率 章末小结复习课(共37张PPT)
文档属性
| 名称 | 第十章 概率 章末小结复习课(共37张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-26 21:18:02 | ||
图片预览











文档简介
(共37张PPT)
第十章 概率 章末复习小结课
人教A版(2019)
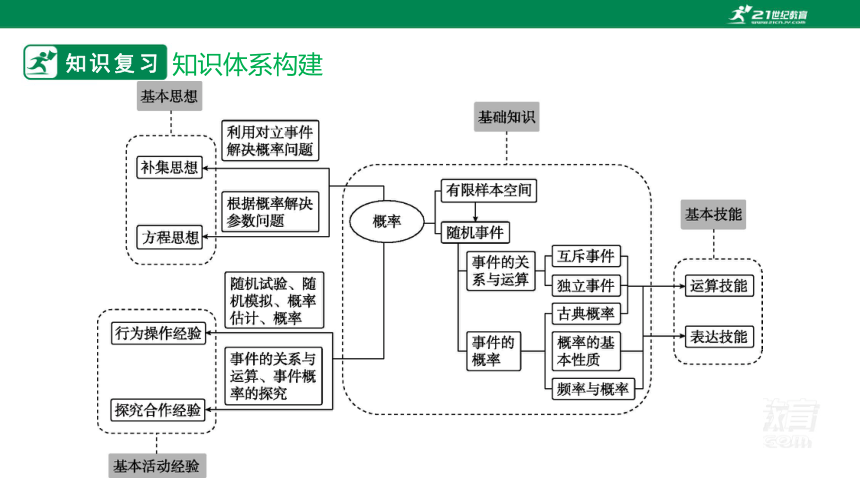
知识复习
知识体系构建
题型探究
知识回顾
1.随机试验的特点
⑴试验可以在相同条件下重复进行;
可重复性
⑵试验的所有可能结果是明确可知的,并且不止一个;
可预知性
⑶每次试验总是恰好出现这些可能结果中的一个,但事先不能确定出现哪一个结果.
随机性
2.样本空间与随机事件
样本点:随机试验E的每个可能的基本结果,用ω表示.
样本空间:全体样本点的集合,用Ω表示.
基本事件:只包含一个样本点的事件.
随机事件(简称事件):样本空间Ω的子集.
必然事件:在每次试验中总有一个样本点发生.
Ω为必然事件.
不可能事件:在每次试验中都不会发生.
为不可能事件.
题型探究
知识回顾
3.事件的关系和运算
含义 符号表示
事件的关系 包含关系
相等关系
互斥关系
对立关系
事件的运算 并事件
交事件
若事件A发生,则必有事件B发生.
A B
如果事件B包含事件A,事件A也包含事件B,即B A且A B.
A=B
事件A与事件B不能同时发生
A∩B=
事件A和事件B在任何一次试验中有且仅有一个发生
A∪B=Ω,且A∩B=
事件A与事件B至少有一个发生
A∪B或A+B
事件A与事件B同时发生
A∩B或AB
题型探究
知识回顾
4.古典概型
⑴特征:
有限性,
等可能性.
⑵计算公式:
P(A).其中n(A)和n(Ω)分别表示事件A和样本空间Ω包含的样本点个数.
5.概率的基本性质
性质1 对任意的事件A,都有P(A)≥0.
性质2 必然事件的概率为1,不可能事件的概率为0.即P(Ω)=1,P( )=0.
性质3 如果事件A与事件B互斥,那么P(A∪B)=P(A)+P(B).
推论 如果事件A1, A2, …, Am两两互斥,那么事件A1∪A2∪…∪Am发生的概率等于这m个事件分别发生的概率之和.即P(A1∪A2∪…∪Am)=P(A1)+P(A2)+…+P(Am).
性质4 如果事件A与事件B互为对立事件,那么P(B)=1-P(A),P(A)=1-P(B).
性质5 如果A B,那么P(A)≤P(B). 对于任意事件A,有0≤P(A)≤1.即P(A)∈[0,1].
性质6 设A、B是一个随机试验中的两个事件,则有P(A∪B)=P(A)+P(B)-P(A∩B).
题型探究
知识回顾
6.独立事件与互斥事件的比较
7.频率与概率
互斥事件 相互独立事件
定义
概率公式
不可能同时发生的两个事件
P(A+B)=P(A)+P(B)
事件A是否发生对事件B发生的概率没有影响
P(AB)=P(A)P(B)
频率 概率
区别 本身是随机的,是一个变量,在试验前不能确定. 是一个确定的数,是客观存在的,与每次的试验无关.
联系 随着试验次数的增加,频率逐渐稳定在概率附近,所以当试验次数比较大时,我们常常用频率估计概率.
题型探究
题型1:互斥事件与对立事件的概率
⑴互斥事件的概率加法公式P(A∪B)=P(A)+P(B)是一个非常重要的公式,运用该公式解题时,首先要分清事件间是否互斥,同时要学会把一个事件拆分为几个互斥事件,然后求出各事件的概率,用概率加法公式得出结果.
⑵当直接计算符合条件的事件个数比较烦琐时,可先计算出其对立事件的个数,求得对立事件的概率,然后利用对立事件的概率加法公式P(A)+P(B)=1,求出符合条件的事件的概率.
题型探究
【例1】玻璃盒子中装有各色球12个,其中5红、4黑、2白、1绿,这些球除颜色外其他完全相同.从中任取1球.设事件A=“取出1个红球”,事件B=“取出1个黑球”,事件C=“取出1个白球”,事件D=“取出1个绿球”.求:
⑴P(A),P(B),P(C),P(D);
⑵“取出1球为红球或黑球”的概率;
⑶“取出1球为红球或黑球或白球”的概率.
解:
⑴P(A)=,P(B)=,P(C)=,P(D)=.
⑵事件A,B,C,D彼此为互斥事件.
“取出1球为红球或黑球”的概率为
题型1:互斥事件与对立事件的概率
P(A∪B)=P(A)+P(B)=.
题型探究
【例1】玻璃盒子中装有各色球12个,其中5红、4黑、2白、1绿,这些球除颜色外其他完全相同.从中任取1球.设事件A=“取出1个红球”,事件B=“取出1个黑球”,事件C=“取出1个白球”,事件D=“取出1个绿球”.求:
⑴P(A),P(B),P(C),P(D);
⑵“取出1球为红球或黑球”的概率;
⑶“取出1球为红球或黑球或白球”的概率.
解:
⑶方法一:“取出1球为红球或黑球或白球”的概率为
P(A∪B∪C)=P(A)+P(B)+P(C)=.
方法二:A∪B∪C的对立事件为D,所以
题型1:互斥事件与对立事件的概率
P(A∪B∪C)=1-P(D)=.
题型探究
题型1:互斥事件与对立事件的概率
求复杂事件的概率通常有两种方法:
⑴将所求事件转化为几个彼此互斥的事件的和事件;
⑵将一个较复杂的事件转化为几个互斥事件的和事件,需要分类较多,而其对立面的分类较少时,可考虑利用对立事件的概率公式,即“正难则反”.它常用来求“至少……”或“至多……”型事件的概率.
初试身手
1.甲、乙两人参加普法知识竞赛,共有5个不同的题目.其中,选择题3个,判断题2个,甲、乙两人各抽一题.
⑴甲、乙两人中有一个抽到选择题,另一个抽到判断题的概率是多少
解:
把3个选择题记为x1,x2,x3,2个判断题记为p1,p2,则试验的样本空间包含的样本点数为5×4=20(个).
⑴设事件A=“甲抽到选择题,乙抽到判断题”,B=“甲抽到判断题,乙抽到选择
题”,M=“甲、乙两人中有一个抽到选择题,另一个抽到判断题”,则M=A∪B.
因为A={(x1,p1),(x1,p2),(x2,p1),(x2,p2),(x3,p1),(x3,p2)},共有6个样本点,B={(p1,x1),
(p1,x2),(p1,x3),(p2,x1),(p2,x2),(p2,x3)},共有6个样本点,
所以P(A)=,P(B)=,
因为事件A与事件B互斥,所以
P(M)=P(A∪B)=P(A)+P(B)=.
则“甲、乙两人中有一个抽到选择题,另一个抽到判断题”的概率为.
题型1:互斥事件与对立事件的概率
初试身手
1.甲、乙两人参加普法知识竞赛,共有5个不同的题目.其中,选择题3个,判断题2个,甲、乙两人各抽一题.
⑵甲、乙两人中至少有一人抽到选择题的概率是多少
解:
⑵设设事件C=“甲、乙两人至少有一人抽到选择题”,则=“甲、乙两人都抽到判断题”={(p1,p2),(p2,p1)},共有2个样本点,P()==,
所以P(C)=1-P()=.
则“甲、乙两人至少有一人抽到选择题”的概率为.
题型1:互斥事件与对立事件的概率
题型探究
题型2:古典概型
求解古典概型概率的“四步”法
注意:
1.试验必须具有古典概型的两大特征——有限性和等可能性.
2.计算基本事件的数目时,要做到不重不漏,常借助坐标系、表格及树状图等列出所有基本事件.
题型探究
【例3】一个袋中装有四个大小、质地完全相同的球,球的编号分别为1,2,3,4.
⑴从袋中随机摸出两个球,求摸出的两个球的编号之和不大于4的概率;
⑵先从袋中随机摸出一个球,该球的编号为m,将球放回袋中,再从袋中随机摸出一个球,该球的编号为n,求n题型2:古典概型
解:
⑴从袋中随机摸出两个球,其样本空间Ω={(1,2),(1,3),(1,4),(2,3),(2,4),(3,4)},共有6个样本点.
设事件A=“摸出的两个球的编号之和不大于4”,
则A={(1,2),(1,3)},共有2个样本点.
因此P(A)=.
题型探究
【例2】一个袋中装有四个大小、质地完全相同的球,球的编号分别为1,2,3,4.
⑴从袋中随机摸出两个球,求摸出的两个球的编号之和不大于4的概率;
⑵先从袋中随机摸出一个球,该球的编号为m,将球放回袋中,再从袋中随机摸出一个球,该球的编号为n,求n题型2:古典概型
解:
⑵先从袋中随机摸出一个球,记下编号为m,放回后,再从袋中随机摸出一个球,记下编号为n,其样本空间
设事件B=“n则P()=.
因此P(B)=1-.
Ω={(1,1),(1,2),(1,3),(1,4),(2,1),(2,2),(2,3),(2,4),(3,1),(3,2),(3,3),
(3,4),(4,1),(4,2),(4,3),(4,4)},共有16个样本点.
题型探究
题型2:古典概型
解决有序和无序问题应注意两点:
⑴关于不放回抽样,计算样本点个数时,既可以看作是有顺序的,也可以看作是无顺序的,其最后结果是一致的.但不论选择哪一种方式,观察的角度必须一致,否则会产生错误.
⑵关于有放回抽样,应注意在连续取出两次的过程中,因为先后顺序不同,所以(a,b),(b,a)不是同一个样本点.
初试身手
2.某科研管理部门为了解下辖的甲、乙、丙三个科研所对重点领域项目的推进情况以便后期工作实施,准备用分层随机抽样的方法从三个科研所中抽取7名科技工作者进行调研,已知三个科研所的人数分别为480,320,320.
⑴应从甲、乙、丙三个科研所中分别抽取多少人
题型2:古典概型
解:
⑴抽样比为,
所以480×=3,320×=2,320×=2,
所以应从甲、乙、丙三个科研所中分别抽取3人、2人、2人.
初试身手
2.某科研管理部门为了解下辖的甲、乙、丙三个科研所对重点领域项目的推进情况以便后期工作实施,准备用分层随机抽样的方法从三个科研所中抽取7名科技工作者进行调研,已知三个科研所的人数分别为480,320,320.
⑵设抽出的7个人分别用A,B,C,D,E,F,G表示,现从中随机抽取2名科研工作者就某一重大项目进行主题发言,求“抽取到的2人来自同一科研所”的概率.
题型2:古典概型
解:
⑵不妨设甲科研所中的3个人为A,B,C,乙科研所中的2个人为D,E,丙科研所的2个为F,G,则从7个人中随机抽取2名科研工作者的基本事件有AB,AC,AD,AE,AF,AG,BC,BD,BE,BF,BG,CD,CE,CF,CG,DE,DF,DG,EF,EG,FG,共有21种,
其中“抽取到的2人来自同一科研所”AB,AC,BC,DE,FG,共5种,
所以“抽取到的2人来自同一科研所”的概率为.
新知探究
题型3:相互独立事件的概率
判断两个事件相互独立的方法:
①直接法:由事件本身的性质直接判断两个事件的发生是否相互影响.
②定义法:P(AB)=P(A)P(B).
P(AB)=P(A)P(B)是事件相互独立的充要条件,也是解答相互独立事件概率问题的唯一工具.另外,公式“P(A∪B)=1-P( )”常用于求相互独立事件至少有一个发生的概率.当题目内涉及“至多”“至少”“恰有”等字眼的概率问题时,要分清事件间的关系.
题型探究
【例3】计算机考试分理论考试与实际操作两部分,每部分考试成绩只记“合格”与“不合格”,两部分考试都“合格”者,则计算机考试“合格”,并颁发合格证书.甲、乙、丙三人在理论考试中“合格”的概率依次为,,,在实际操作考试中“合格”的概率依次为,,,所有考试是否合格相互之间没有影响.
⑴假设甲、乙、丙三人同时进行理论与实际操作两项考试,谁获得合格证书的可能性最大?
解:
⑴设“甲获得合格证书”为事件A,“乙获得合格证书”为事件B,“丙获得合格证书”为事件C,则
所以丙获得合格证书的可能性最大.
P(A)=,
P(B)=,
P(C)=.
因为P(C)>P(B)>P(A),
题型3:相互独立事件的概率
题型探究
【例3】计算机考试分理论考试与实际操作两部分,每部分考试成绩只记“合格”与“不合格”,两部分考试都“合格”者,则计算机考试“合格”,并颁发合格证书.甲、乙、丙三人在理论考试中“合格”的概率依次为,,,在实际操作考试中“合格”的概率依次为,,,所有考试是否合格相互之间没有影响.
⑵这三人进行理论与实际操作两项考试后,求恰有两人获得合格证书的概率.
解:
⑵设“三人考试后恰有两人获得合格证书”为事件D,则
所以恰有两人获得合格证书的概率为.
P(D)=P(AB)+P(AC)+P(BC)
=,
题型3:相互独立事件的概率
题型探究
题型3:相互独立事件的概率
应用相互独立事件同时发生的概率的乘法公式求概率的解题步骤:
⑴确定各事件是相互独立的.
⑵确定各事件会同时发生.
⑶先求每个事件发生的概率,再求其积.
初试身手
3.在某校年度足球比赛中,经过激烈角逐后,最终A,B,C,D四个班级的球队闯入半决赛.在半决赛中,对阵形式为:A对阵C,B对阵D,获胜球队进入决赛争夺冠、亚军,失利球队争夺三、四名.若每场比赛是相互独立的,四支球队间相互对阵获胜的概率如下表所示:
则A队最终获得冠军的概率为________.
题型3:相互独立事件的概率
A B C D
A获胜概率 0.3 0.4 0.8
B获胜概率 0.7 0.7 0.5
C获胜概率 0.6 0.3 0.3
D获胜概率 0.2 0.5 0.7
A胜C的概率为0.4,B胜D且A胜B的概率为0.5×0.3=0.15,D胜B且A胜D的概率为0.5×0.8=0.4,
解:
则A队最终获得冠军的概率为0.4×0.15+0.4×0.4=0.22.
0.22
题型探究
题型4:用频率估计概率
用频率估计概率的步骤:
⑴进行大量的随机试验,得频数;
⑶由频率与概率的关系,估计概率值.
⑵由频率计算公式,得频率;
在大量重复进行同一试验时,事件A发生的频率总接近于某个常数,并在这个常数附近摆动,这时就把这个常数称为事件A的概率,记作P(A).
根据定义可知0≤P(A)≤1,显然必然事件的概率是1,不可能事件的概率是0.
题型探究
【例4】对一批U盘进行抽检,结果见下表:
⑴计算表中次品的频率(结果保留到小数点后三位);
⑵从这批U盘中任意抽取一个是次品的概率约是多少
⑶为保证买到次品的顾客能够及时更换,要销售2 000个U盘,至少需进货多少个U盘
题型4:用频率估计概率
抽出件数a/件 50 100 200 300 400 500
次品件数b/件 3 4 5 5 8 9
次品频率
解:
⑴表中次品频率从左到右依次为0.060,0.040,0.025,0.017,0.020,0.018.
⑵当抽取件数a越来越大时,出现次品的频率在0.02附近摆动,所以从这批U盘中任意抽取一个是次品的概率约是0.02.
⑶设需要进货x个U盘,为保证其中有2000个正品U盘,则
x(1-0.02)≥2000,解得x≥2041,
因为x是正整数,则至少需进货2041个U盘.
初试身手
4.某射击运动员为某运动会做准备,在相同条件下进行射击训练,结果如下:
⑴该射击运动员射击一次,击中靶心的概率大约是多少
⑵假设该射击运动员射击了300次,则击中靶心的次数大约是多少
题型4:用频率估计概率
射击次数n 10 20 50 100 200 500
击中靶心次数m 8 19 44 92 178 455
击中靶心的频率 0.8 0.95 0.88 0.92 0.89 0.91
解:
⑴由题意,击中靶心的频率与0.9接近,则概率约为0.9.
⑵由⑴可得,击中靶心的次数大约为300×0.9=270(次).
初试身手
4.某射击运动员为某运动会做准备,在相同条件下进行射击训练,结果如下:
⑶假如该射击运动员射击了300次,前270次都击中靶心,那么后30次一定都击不中靶心吗
⑷假如该射击运动员射击了10次,前9次中有8次击中靶心,那么第10次一定击中靶心吗
题型4:用频率估计概率
射击次数n 10 20 50 100 200 500
击中靶心次数m 8 19 44 92 178 455
击中靶心的频率 0.8 0.95 0.88 0.92 0.89 0.91
解:
⑶由概率的意义,可知概率是个常数,不因试验次数的变化而变化.后30次中,每次击中靶心的概率仍是0.9,所以不一定不击中靶心.
⑷不一定.
题型探究
题型5:概率与统计的综合应用
概率与统计相结合,所涉及的统计知识是基础知识,所涉及的概率往往是古典概型,虽然是综合题,但是难度不大.关键是把相关的知识转化为事件,然后利用古典概型的有关知识解决,一般步骤为:
⑴将题目条件中的相关知识转化为事件;
⑵判断事件是否为古典概型;
⑶选用合适的方法确定基本事件个数;
⑷代入古典概型的概率公式求解.
题型探究
【例5】某班同学利用国庆节进行社会实践,对[25,55]岁的人群随机抽取n人进行了一次生活习惯是否符合低碳观念的调查,若生活习惯符合低碳观念的称为“低碳族”,否则称为“非低碳族”,得到如下表和各年龄段人数的频率分布直方图:
⑴补全频率分布直方图并求n,a,p的值;
⑵从年龄段在[40,50)的“低碳族”中采用样本量按比例分配的分层抽样法抽取6人参加户外低碳体验活动,其中选取2人作为领队,求选取的2名领队中恰有1人年龄在[40,45)岁的概率.
题型5:概率与统计的综合应用
题型探究
解:
⑴∵第二组频率为1-(0.04+0.04+0.03+0.02+0.01)×5=0.3
∴高为=0.06,频率直方图如右图.
第一组人数为=200,频率为0.04×5=0.2.
∴n==1000
∴第二组的人数为0.3×1000=300,
∴p==0.65.
由图知第四组的频率为0.03×5=0.15,
∴第四组的人数为0.15×1000=150,
∴a=0.4×150=60.
⑵∵[40,45)年龄段的“低碳族”与[45,50)年龄段的“低碳族”的比值为 60:30
=2:1,∴采取分层抽样抽取6人,[40,45)岁中有4人,[45,50)岁中有2人.
设[40,45)岁中的4人为a,b,c,d,[45,50)岁中的2人为m,n,则选取2人作为领队的有(a,b),(a,c),(a.d),(a,m),(a,n),(b,c),(b,d),(b,m),(b,n),(c,d),(c,m),(c,n),(d,m),(d,n),
(m,n),共15种.
其中恰有1人年龄在[40,45)岁的有(a,m),(a,n),(b,m),(b,n),(c,m),(c,n),(d,m),(d,n)共8种.
∴选取的2名领队中恰有1人年龄在[40,45)岁的概率为.
题型5:概率与统计的综合应用
初试身手
5.某市城管委对所在城市约6 000个流动个体经营者进行调查
统计,发现所售商品多为小吃、衣帽、果蔬、玩具、饰品等,
各类个体经营者所占比例如图1.
⑴该市城管委为了更好地服务百姓,打算从流动个体经营者经
营点中随机抽取100个进行政策问询.如果按照分层随机抽样
的方法抽取,请问应抽取小吃类、果蔬类流动个体经营者各多少
解:
按照分层随机抽样的方法抽取,应抽取小吃类流动个体经营者为
100×40%=40(个),
果蔬类流动个体经营者为100×15%=15(个).
题型5:概率与统计的综合应用
⑴由题意知,小吃类流动个体经营者所占比例为1-25%-15%-10%-5%-5%=40%,
初试身手
5.某市城管委对所在城市约6 000个流动个体经营者进行调查
统计,发现所售商品多为小吃、衣帽、果蔬、玩具、饰品等,
各类个体经营者所占比例如图1.
⑵为了更好地了解流动个体经营者的收入情况,工作人员还对
某果蔬经营点最近40天的日收入(单位:元)进行了统计,所得
频率分布直方图如图2.若从该果蔬经营点的日收入超过200元的天数中随机抽取两天,求这两天的日收入至少有一天超过250元的概率.
题型5:概率与统计的综合应用
初试身手
5.某市城管委对所在城市约6 000个流动个体经营者进行调查
统计,发现所售商品多为小吃、衣帽、果蔬、玩具、饰品等,
各类个体经营者所占比例如图1.
⑵为了更好地了解流动个体经营者的收入情况,工作人员还对
某果蔬经营点最近40天的日收入(单位:元)进行了统计,所得
频率分布直方图如图2.若从该果蔬经营点的日收入超过200元的天数中随机抽取两天,求这两天的日收入至少有一天超过250元的概率.
解:
记日收入超过250元的2天为a1,a2,其余4天为b1,b2,b3,b4,随机抽取两天的所有可能情况有(a1,a2),(a1,b1),(a1,b2),(a1,b3),(a1,b4),(a2,b1),(a2,b2),(a2,b3),
(a2,b4),(b1,b2),(b1,b3),(b1,b4),(b2,b3),(b2,b4),(b3,b4),共15种,
所以这两天的日收入至少有一天超过250元的概率为P=.
题型5:概率与统计的综合应用
⑵该果蔬经营点的日收入超过200元的天数为(0.002+0.001)×50×40=6(天),
其中超过250元的有40×0.001×50=2(天).
其中至少有一天超过250元的所有可能情况有(a1,a2),(a1,b1),(a1,b2),(a1,b3),(a1,b4),
(a2,b1),(a2,b2),(a2,b3),(a2,b4),共9种.
作业布置
作业: p266-267 复习参考题10 第3,4,5,6,7题.
尽情享受学习数学的快乐吧!
我们下节课再见!
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
第十章 概率 章末复习小结课
人教A版(2019)
知识复习
知识体系构建
题型探究
知识回顾
1.随机试验的特点
⑴试验可以在相同条件下重复进行;
可重复性
⑵试验的所有可能结果是明确可知的,并且不止一个;
可预知性
⑶每次试验总是恰好出现这些可能结果中的一个,但事先不能确定出现哪一个结果.
随机性
2.样本空间与随机事件
样本点:随机试验E的每个可能的基本结果,用ω表示.
样本空间:全体样本点的集合,用Ω表示.
基本事件:只包含一个样本点的事件.
随机事件(简称事件):样本空间Ω的子集.
必然事件:在每次试验中总有一个样本点发生.
Ω为必然事件.
不可能事件:在每次试验中都不会发生.
为不可能事件.
题型探究
知识回顾
3.事件的关系和运算
含义 符号表示
事件的关系 包含关系
相等关系
互斥关系
对立关系
事件的运算 并事件
交事件
若事件A发生,则必有事件B发生.
A B
如果事件B包含事件A,事件A也包含事件B,即B A且A B.
A=B
事件A与事件B不能同时发生
A∩B=
事件A和事件B在任何一次试验中有且仅有一个发生
A∪B=Ω,且A∩B=
事件A与事件B至少有一个发生
A∪B或A+B
事件A与事件B同时发生
A∩B或AB
题型探究
知识回顾
4.古典概型
⑴特征:
有限性,
等可能性.
⑵计算公式:
P(A).其中n(A)和n(Ω)分别表示事件A和样本空间Ω包含的样本点个数.
5.概率的基本性质
性质1 对任意的事件A,都有P(A)≥0.
性质2 必然事件的概率为1,不可能事件的概率为0.即P(Ω)=1,P( )=0.
性质3 如果事件A与事件B互斥,那么P(A∪B)=P(A)+P(B).
推论 如果事件A1, A2, …, Am两两互斥,那么事件A1∪A2∪…∪Am发生的概率等于这m个事件分别发生的概率之和.即P(A1∪A2∪…∪Am)=P(A1)+P(A2)+…+P(Am).
性质4 如果事件A与事件B互为对立事件,那么P(B)=1-P(A),P(A)=1-P(B).
性质5 如果A B,那么P(A)≤P(B). 对于任意事件A,有0≤P(A)≤1.即P(A)∈[0,1].
性质6 设A、B是一个随机试验中的两个事件,则有P(A∪B)=P(A)+P(B)-P(A∩B).
题型探究
知识回顾
6.独立事件与互斥事件的比较
7.频率与概率
互斥事件 相互独立事件
定义
概率公式
不可能同时发生的两个事件
P(A+B)=P(A)+P(B)
事件A是否发生对事件B发生的概率没有影响
P(AB)=P(A)P(B)
频率 概率
区别 本身是随机的,是一个变量,在试验前不能确定. 是一个确定的数,是客观存在的,与每次的试验无关.
联系 随着试验次数的增加,频率逐渐稳定在概率附近,所以当试验次数比较大时,我们常常用频率估计概率.
题型探究
题型1:互斥事件与对立事件的概率
⑴互斥事件的概率加法公式P(A∪B)=P(A)+P(B)是一个非常重要的公式,运用该公式解题时,首先要分清事件间是否互斥,同时要学会把一个事件拆分为几个互斥事件,然后求出各事件的概率,用概率加法公式得出结果.
⑵当直接计算符合条件的事件个数比较烦琐时,可先计算出其对立事件的个数,求得对立事件的概率,然后利用对立事件的概率加法公式P(A)+P(B)=1,求出符合条件的事件的概率.
题型探究
【例1】玻璃盒子中装有各色球12个,其中5红、4黑、2白、1绿,这些球除颜色外其他完全相同.从中任取1球.设事件A=“取出1个红球”,事件B=“取出1个黑球”,事件C=“取出1个白球”,事件D=“取出1个绿球”.求:
⑴P(A),P(B),P(C),P(D);
⑵“取出1球为红球或黑球”的概率;
⑶“取出1球为红球或黑球或白球”的概率.
解:
⑴P(A)=,P(B)=,P(C)=,P(D)=.
⑵事件A,B,C,D彼此为互斥事件.
“取出1球为红球或黑球”的概率为
题型1:互斥事件与对立事件的概率
P(A∪B)=P(A)+P(B)=.
题型探究
【例1】玻璃盒子中装有各色球12个,其中5红、4黑、2白、1绿,这些球除颜色外其他完全相同.从中任取1球.设事件A=“取出1个红球”,事件B=“取出1个黑球”,事件C=“取出1个白球”,事件D=“取出1个绿球”.求:
⑴P(A),P(B),P(C),P(D);
⑵“取出1球为红球或黑球”的概率;
⑶“取出1球为红球或黑球或白球”的概率.
解:
⑶方法一:“取出1球为红球或黑球或白球”的概率为
P(A∪B∪C)=P(A)+P(B)+P(C)=.
方法二:A∪B∪C的对立事件为D,所以
题型1:互斥事件与对立事件的概率
P(A∪B∪C)=1-P(D)=.
题型探究
题型1:互斥事件与对立事件的概率
求复杂事件的概率通常有两种方法:
⑴将所求事件转化为几个彼此互斥的事件的和事件;
⑵将一个较复杂的事件转化为几个互斥事件的和事件,需要分类较多,而其对立面的分类较少时,可考虑利用对立事件的概率公式,即“正难则反”.它常用来求“至少……”或“至多……”型事件的概率.
初试身手
1.甲、乙两人参加普法知识竞赛,共有5个不同的题目.其中,选择题3个,判断题2个,甲、乙两人各抽一题.
⑴甲、乙两人中有一个抽到选择题,另一个抽到判断题的概率是多少
解:
把3个选择题记为x1,x2,x3,2个判断题记为p1,p2,则试验的样本空间包含的样本点数为5×4=20(个).
⑴设事件A=“甲抽到选择题,乙抽到判断题”,B=“甲抽到判断题,乙抽到选择
题”,M=“甲、乙两人中有一个抽到选择题,另一个抽到判断题”,则M=A∪B.
因为A={(x1,p1),(x1,p2),(x2,p1),(x2,p2),(x3,p1),(x3,p2)},共有6个样本点,B={(p1,x1),
(p1,x2),(p1,x3),(p2,x1),(p2,x2),(p2,x3)},共有6个样本点,
所以P(A)=,P(B)=,
因为事件A与事件B互斥,所以
P(M)=P(A∪B)=P(A)+P(B)=.
则“甲、乙两人中有一个抽到选择题,另一个抽到判断题”的概率为.
题型1:互斥事件与对立事件的概率
初试身手
1.甲、乙两人参加普法知识竞赛,共有5个不同的题目.其中,选择题3个,判断题2个,甲、乙两人各抽一题.
⑵甲、乙两人中至少有一人抽到选择题的概率是多少
解:
⑵设设事件C=“甲、乙两人至少有一人抽到选择题”,则=“甲、乙两人都抽到判断题”={(p1,p2),(p2,p1)},共有2个样本点,P()==,
所以P(C)=1-P()=.
则“甲、乙两人至少有一人抽到选择题”的概率为.
题型1:互斥事件与对立事件的概率
题型探究
题型2:古典概型
求解古典概型概率的“四步”法
注意:
1.试验必须具有古典概型的两大特征——有限性和等可能性.
2.计算基本事件的数目时,要做到不重不漏,常借助坐标系、表格及树状图等列出所有基本事件.
题型探究
【例3】一个袋中装有四个大小、质地完全相同的球,球的编号分别为1,2,3,4.
⑴从袋中随机摸出两个球,求摸出的两个球的编号之和不大于4的概率;
⑵先从袋中随机摸出一个球,该球的编号为m,将球放回袋中,再从袋中随机摸出一个球,该球的编号为n,求n
解:
⑴从袋中随机摸出两个球,其样本空间Ω={(1,2),(1,3),(1,4),(2,3),(2,4),(3,4)},共有6个样本点.
设事件A=“摸出的两个球的编号之和不大于4”,
则A={(1,2),(1,3)},共有2个样本点.
因此P(A)=.
题型探究
【例2】一个袋中装有四个大小、质地完全相同的球,球的编号分别为1,2,3,4.
⑴从袋中随机摸出两个球,求摸出的两个球的编号之和不大于4的概率;
⑵先从袋中随机摸出一个球,该球的编号为m,将球放回袋中,再从袋中随机摸出一个球,该球的编号为n,求n
解:
⑵先从袋中随机摸出一个球,记下编号为m,放回后,再从袋中随机摸出一个球,记下编号为n,其样本空间
设事件B=“n
因此P(B)=1-.
Ω={(1,1),(1,2),(1,3),(1,4),(2,1),(2,2),(2,3),(2,4),(3,1),(3,2),(3,3),
(3,4),(4,1),(4,2),(4,3),(4,4)},共有16个样本点.
题型探究
题型2:古典概型
解决有序和无序问题应注意两点:
⑴关于不放回抽样,计算样本点个数时,既可以看作是有顺序的,也可以看作是无顺序的,其最后结果是一致的.但不论选择哪一种方式,观察的角度必须一致,否则会产生错误.
⑵关于有放回抽样,应注意在连续取出两次的过程中,因为先后顺序不同,所以(a,b),(b,a)不是同一个样本点.
初试身手
2.某科研管理部门为了解下辖的甲、乙、丙三个科研所对重点领域项目的推进情况以便后期工作实施,准备用分层随机抽样的方法从三个科研所中抽取7名科技工作者进行调研,已知三个科研所的人数分别为480,320,320.
⑴应从甲、乙、丙三个科研所中分别抽取多少人
题型2:古典概型
解:
⑴抽样比为,
所以480×=3,320×=2,320×=2,
所以应从甲、乙、丙三个科研所中分别抽取3人、2人、2人.
初试身手
2.某科研管理部门为了解下辖的甲、乙、丙三个科研所对重点领域项目的推进情况以便后期工作实施,准备用分层随机抽样的方法从三个科研所中抽取7名科技工作者进行调研,已知三个科研所的人数分别为480,320,320.
⑵设抽出的7个人分别用A,B,C,D,E,F,G表示,现从中随机抽取2名科研工作者就某一重大项目进行主题发言,求“抽取到的2人来自同一科研所”的概率.
题型2:古典概型
解:
⑵不妨设甲科研所中的3个人为A,B,C,乙科研所中的2个人为D,E,丙科研所的2个为F,G,则从7个人中随机抽取2名科研工作者的基本事件有AB,AC,AD,AE,AF,AG,BC,BD,BE,BF,BG,CD,CE,CF,CG,DE,DF,DG,EF,EG,FG,共有21种,
其中“抽取到的2人来自同一科研所”AB,AC,BC,DE,FG,共5种,
所以“抽取到的2人来自同一科研所”的概率为.
新知探究
题型3:相互独立事件的概率
判断两个事件相互独立的方法:
①直接法:由事件本身的性质直接判断两个事件的发生是否相互影响.
②定义法:P(AB)=P(A)P(B).
P(AB)=P(A)P(B)是事件相互独立的充要条件,也是解答相互独立事件概率问题的唯一工具.另外,公式“P(A∪B)=1-P( )”常用于求相互独立事件至少有一个发生的概率.当题目内涉及“至多”“至少”“恰有”等字眼的概率问题时,要分清事件间的关系.
题型探究
【例3】计算机考试分理论考试与实际操作两部分,每部分考试成绩只记“合格”与“不合格”,两部分考试都“合格”者,则计算机考试“合格”,并颁发合格证书.甲、乙、丙三人在理论考试中“合格”的概率依次为,,,在实际操作考试中“合格”的概率依次为,,,所有考试是否合格相互之间没有影响.
⑴假设甲、乙、丙三人同时进行理论与实际操作两项考试,谁获得合格证书的可能性最大?
解:
⑴设“甲获得合格证书”为事件A,“乙获得合格证书”为事件B,“丙获得合格证书”为事件C,则
所以丙获得合格证书的可能性最大.
P(A)=,
P(B)=,
P(C)=.
因为P(C)>P(B)>P(A),
题型3:相互独立事件的概率
题型探究
【例3】计算机考试分理论考试与实际操作两部分,每部分考试成绩只记“合格”与“不合格”,两部分考试都“合格”者,则计算机考试“合格”,并颁发合格证书.甲、乙、丙三人在理论考试中“合格”的概率依次为,,,在实际操作考试中“合格”的概率依次为,,,所有考试是否合格相互之间没有影响.
⑵这三人进行理论与实际操作两项考试后,求恰有两人获得合格证书的概率.
解:
⑵设“三人考试后恰有两人获得合格证书”为事件D,则
所以恰有两人获得合格证书的概率为.
P(D)=P(AB)+P(AC)+P(BC)
=,
题型3:相互独立事件的概率
题型探究
题型3:相互独立事件的概率
应用相互独立事件同时发生的概率的乘法公式求概率的解题步骤:
⑴确定各事件是相互独立的.
⑵确定各事件会同时发生.
⑶先求每个事件发生的概率,再求其积.
初试身手
3.在某校年度足球比赛中,经过激烈角逐后,最终A,B,C,D四个班级的球队闯入半决赛.在半决赛中,对阵形式为:A对阵C,B对阵D,获胜球队进入决赛争夺冠、亚军,失利球队争夺三、四名.若每场比赛是相互独立的,四支球队间相互对阵获胜的概率如下表所示:
则A队最终获得冠军的概率为________.
题型3:相互独立事件的概率
A B C D
A获胜概率 0.3 0.4 0.8
B获胜概率 0.7 0.7 0.5
C获胜概率 0.6 0.3 0.3
D获胜概率 0.2 0.5 0.7
A胜C的概率为0.4,B胜D且A胜B的概率为0.5×0.3=0.15,D胜B且A胜D的概率为0.5×0.8=0.4,
解:
则A队最终获得冠军的概率为0.4×0.15+0.4×0.4=0.22.
0.22
题型探究
题型4:用频率估计概率
用频率估计概率的步骤:
⑴进行大量的随机试验,得频数;
⑶由频率与概率的关系,估计概率值.
⑵由频率计算公式,得频率;
在大量重复进行同一试验时,事件A发生的频率总接近于某个常数,并在这个常数附近摆动,这时就把这个常数称为事件A的概率,记作P(A).
根据定义可知0≤P(A)≤1,显然必然事件的概率是1,不可能事件的概率是0.
题型探究
【例4】对一批U盘进行抽检,结果见下表:
⑴计算表中次品的频率(结果保留到小数点后三位);
⑵从这批U盘中任意抽取一个是次品的概率约是多少
⑶为保证买到次品的顾客能够及时更换,要销售2 000个U盘,至少需进货多少个U盘
题型4:用频率估计概率
抽出件数a/件 50 100 200 300 400 500
次品件数b/件 3 4 5 5 8 9
次品频率
解:
⑴表中次品频率从左到右依次为0.060,0.040,0.025,0.017,0.020,0.018.
⑵当抽取件数a越来越大时,出现次品的频率在0.02附近摆动,所以从这批U盘中任意抽取一个是次品的概率约是0.02.
⑶设需要进货x个U盘,为保证其中有2000个正品U盘,则
x(1-0.02)≥2000,解得x≥2041,
因为x是正整数,则至少需进货2041个U盘.
初试身手
4.某射击运动员为某运动会做准备,在相同条件下进行射击训练,结果如下:
⑴该射击运动员射击一次,击中靶心的概率大约是多少
⑵假设该射击运动员射击了300次,则击中靶心的次数大约是多少
题型4:用频率估计概率
射击次数n 10 20 50 100 200 500
击中靶心次数m 8 19 44 92 178 455
击中靶心的频率 0.8 0.95 0.88 0.92 0.89 0.91
解:
⑴由题意,击中靶心的频率与0.9接近,则概率约为0.9.
⑵由⑴可得,击中靶心的次数大约为300×0.9=270(次).
初试身手
4.某射击运动员为某运动会做准备,在相同条件下进行射击训练,结果如下:
⑶假如该射击运动员射击了300次,前270次都击中靶心,那么后30次一定都击不中靶心吗
⑷假如该射击运动员射击了10次,前9次中有8次击中靶心,那么第10次一定击中靶心吗
题型4:用频率估计概率
射击次数n 10 20 50 100 200 500
击中靶心次数m 8 19 44 92 178 455
击中靶心的频率 0.8 0.95 0.88 0.92 0.89 0.91
解:
⑶由概率的意义,可知概率是个常数,不因试验次数的变化而变化.后30次中,每次击中靶心的概率仍是0.9,所以不一定不击中靶心.
⑷不一定.
题型探究
题型5:概率与统计的综合应用
概率与统计相结合,所涉及的统计知识是基础知识,所涉及的概率往往是古典概型,虽然是综合题,但是难度不大.关键是把相关的知识转化为事件,然后利用古典概型的有关知识解决,一般步骤为:
⑴将题目条件中的相关知识转化为事件;
⑵判断事件是否为古典概型;
⑶选用合适的方法确定基本事件个数;
⑷代入古典概型的概率公式求解.
题型探究
【例5】某班同学利用国庆节进行社会实践,对[25,55]岁的人群随机抽取n人进行了一次生活习惯是否符合低碳观念的调查,若生活习惯符合低碳观念的称为“低碳族”,否则称为“非低碳族”,得到如下表和各年龄段人数的频率分布直方图:
⑴补全频率分布直方图并求n,a,p的值;
⑵从年龄段在[40,50)的“低碳族”中采用样本量按比例分配的分层抽样法抽取6人参加户外低碳体验活动,其中选取2人作为领队,求选取的2名领队中恰有1人年龄在[40,45)岁的概率.
题型5:概率与统计的综合应用
题型探究
解:
⑴∵第二组频率为1-(0.04+0.04+0.03+0.02+0.01)×5=0.3
∴高为=0.06,频率直方图如右图.
第一组人数为=200,频率为0.04×5=0.2.
∴n==1000
∴第二组的人数为0.3×1000=300,
∴p==0.65.
由图知第四组的频率为0.03×5=0.15,
∴第四组的人数为0.15×1000=150,
∴a=0.4×150=60.
⑵∵[40,45)年龄段的“低碳族”与[45,50)年龄段的“低碳族”的比值为 60:30
=2:1,∴采取分层抽样抽取6人,[40,45)岁中有4人,[45,50)岁中有2人.
设[40,45)岁中的4人为a,b,c,d,[45,50)岁中的2人为m,n,则选取2人作为领队的有(a,b),(a,c),(a.d),(a,m),(a,n),(b,c),(b,d),(b,m),(b,n),(c,d),(c,m),(c,n),(d,m),(d,n),
(m,n),共15种.
其中恰有1人年龄在[40,45)岁的有(a,m),(a,n),(b,m),(b,n),(c,m),(c,n),(d,m),(d,n)共8种.
∴选取的2名领队中恰有1人年龄在[40,45)岁的概率为.
题型5:概率与统计的综合应用
初试身手
5.某市城管委对所在城市约6 000个流动个体经营者进行调查
统计,发现所售商品多为小吃、衣帽、果蔬、玩具、饰品等,
各类个体经营者所占比例如图1.
⑴该市城管委为了更好地服务百姓,打算从流动个体经营者经
营点中随机抽取100个进行政策问询.如果按照分层随机抽样
的方法抽取,请问应抽取小吃类、果蔬类流动个体经营者各多少
解:
按照分层随机抽样的方法抽取,应抽取小吃类流动个体经营者为
100×40%=40(个),
果蔬类流动个体经营者为100×15%=15(个).
题型5:概率与统计的综合应用
⑴由题意知,小吃类流动个体经营者所占比例为1-25%-15%-10%-5%-5%=40%,
初试身手
5.某市城管委对所在城市约6 000个流动个体经营者进行调查
统计,发现所售商品多为小吃、衣帽、果蔬、玩具、饰品等,
各类个体经营者所占比例如图1.
⑵为了更好地了解流动个体经营者的收入情况,工作人员还对
某果蔬经营点最近40天的日收入(单位:元)进行了统计,所得
频率分布直方图如图2.若从该果蔬经营点的日收入超过200元的天数中随机抽取两天,求这两天的日收入至少有一天超过250元的概率.
题型5:概率与统计的综合应用
初试身手
5.某市城管委对所在城市约6 000个流动个体经营者进行调查
统计,发现所售商品多为小吃、衣帽、果蔬、玩具、饰品等,
各类个体经营者所占比例如图1.
⑵为了更好地了解流动个体经营者的收入情况,工作人员还对
某果蔬经营点最近40天的日收入(单位:元)进行了统计,所得
频率分布直方图如图2.若从该果蔬经营点的日收入超过200元的天数中随机抽取两天,求这两天的日收入至少有一天超过250元的概率.
解:
记日收入超过250元的2天为a1,a2,其余4天为b1,b2,b3,b4,随机抽取两天的所有可能情况有(a1,a2),(a1,b1),(a1,b2),(a1,b3),(a1,b4),(a2,b1),(a2,b2),(a2,b3),
(a2,b4),(b1,b2),(b1,b3),(b1,b4),(b2,b3),(b2,b4),(b3,b4),共15种,
所以这两天的日收入至少有一天超过250元的概率为P=.
题型5:概率与统计的综合应用
⑵该果蔬经营点的日收入超过200元的天数为(0.002+0.001)×50×40=6(天),
其中超过250元的有40×0.001×50=2(天).
其中至少有一天超过250元的所有可能情况有(a1,a2),(a1,b1),(a1,b2),(a1,b3),(a1,b4),
(a2,b1),(a2,b2),(a2,b3),(a2,b4),共9种.
作业布置
作业: p266-267 复习参考题10 第3,4,5,6,7题.
尽情享受学习数学的快乐吧!
我们下节课再见!
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
