山东省东营市东凯实验学校2022-2023学年六年级下学期期中考试数学试卷(A卷)(五四制)(含解析)
文档属性
| 名称 | 山东省东营市东凯实验学校2022-2023学年六年级下学期期中考试数学试卷(A卷)(五四制)(含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 639.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-25 00:00:00 | ||
图片预览



文档简介
山东省东营市东凯实验学校2022-2023学年六年级(下)期中数学试卷(A卷)(五四学制)
一.选择题(共10小题,每题3分,满分30分)
1.(3分)下列所示的图案分别是奔驰、雪铁龙、大众、三菱汽车的车标,其中可以看作由“基本图案”经过平移得到的是( )
A. B. C. D.
2.(3分)如图是一跳远运动员跳落沙坑时留下的痕迹,P1,P2,P3是三次跳远的落点,则表示该运动员成绩的是( )
A.线段AP1的长 B.线段AP2的长
C.线段BP3的长 D.线段CP3的长
3.(3分)如图,将正方体的平面展开图重新折成正方体后,“数”字对面的字是( )
A.喜 B.欢 C.我 D.学
4.(3分)如图,下列说法错误的是( )
A.∠C与∠1是内错角 B.∠2与∠A是内错角
C.∠A与∠B是同旁内角 D.∠A与∠3是同位角
5.(3分)一个正方形的面积是30,估计它的边长的大小在( )
A.3与4之间 B.4与5之间 C.5与6之间 D.6与7之间
6.(3分)下列命题中真命题的个数有( )
(1)过一点有且只有一条直线与已知直线垂直
(2)负数没有算术平方根
(3)两条平行线被第三条直线所截,内错角的平分线互相平行
(4)射线AO和射线OA是同一条射线
(5)若一个角的两边与另一个角的两边平行,则这两个角相等
A.1个 B.2个 C.3个 D.4个
7.(3分)如图,已知线段AB,延长AB至C,使得BC=AB,若D是BC的中点,CD=2cm,则AC的长等于( )
A.4cm B.8cm C.10cm D.12cm
8.(3分)如图,直线AB,CD相交于点O,EO⊥AB,垂足为O,∠AOC=50°,则∠DOE的度数为( )
A.50° B.40° C.30° D.20°
9.(3分)如图,长方形纸带ABCD中,AB∥CD,将纸带沿EF折叠,A、D两点分别落在A'、D′处,若∠1=62°,则∠2的大小是( )
A.46° B.56° C.62° D.72°
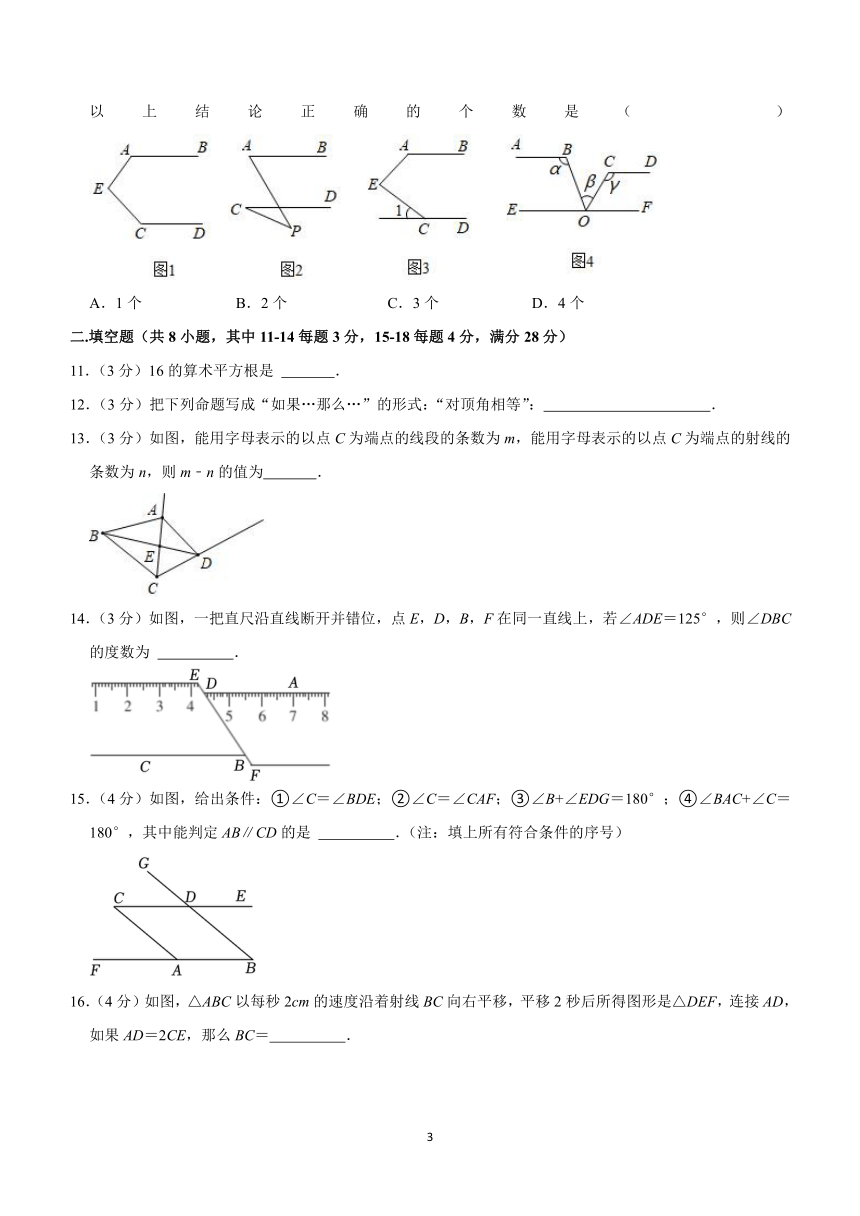
10.(3分)①如图1,AB∥CD,则∠A+∠E+∠C=360°;
②如图2,AB∥CD,则∠P=∠A﹣∠C;
③如图3,AB∥CD,则∠E=∠A+∠1;
④如图4,直线AB∥CD∥EF,点O在直线EF上,则∠α﹣∠β+∠γ=180°.
以上结论正确的个数是( )
A.1个 B.2个 C.3个 D.4个
二.填空题(共8小题,其中11-14每题3分,15-18每题4分,满分28分)
11.(3分)16的算术平方根是 .
12.(3分)把下列命题写成“如果…那么…”的形式:“对顶角相等”: .
13.(3分)如图,能用字母表示的以点C为端点的线段的条数为m,能用字母表示的以点C为端点的射线的条数为n,则m﹣n的值为 .
14.(3分)如图,一把直尺沿直线断开并错位,点E,D,B,F在同一直线上,若∠ADE=125°,则∠DBC的度数为 .
15.(4分)如图,给出条件:①∠C=∠BDE;②∠C=∠CAF;③∠B+∠EDG=180°;④∠BAC+∠C=180°,其中能判定AB∥CD的是 .(注:填上所有符合条件的序号)
16.(4分)如图,△ABC以每秒2cm的速度沿着射线BC向右平移,平移2秒后所得图形是△DEF,连接AD,如果AD=2CE,那么BC= .
17.(4分)如图摆放的一副学生用直角三角板,∠F=30°,∠C=45°,AB与DE相交于点G,当EF∥BC时,∠EGB的度数是 .
18.(4分)下面是一个按某种规律排列的数阵:
根据数阵排列的规律,第n(n是整数,且n≥3)行从左向右数第n﹣2个数是 (用含n的代数式表示)
三、解答题(共7小题,满分62分)
19.(8分)如图,已知直线l和直线外三点A,B,C,按下列要求画图:
(1)画射线CA,画直线BC;(只画图,不写作法不写结论)
(2)画点A到l的垂线段,垂足为D;(只画图,不写作法不写结论)
(3)过点B作直线l的平行直线m;(只画图,不写作法不写结论)
(4)在直线l上确定出点BE,使得AE+BE最小,理由是 .
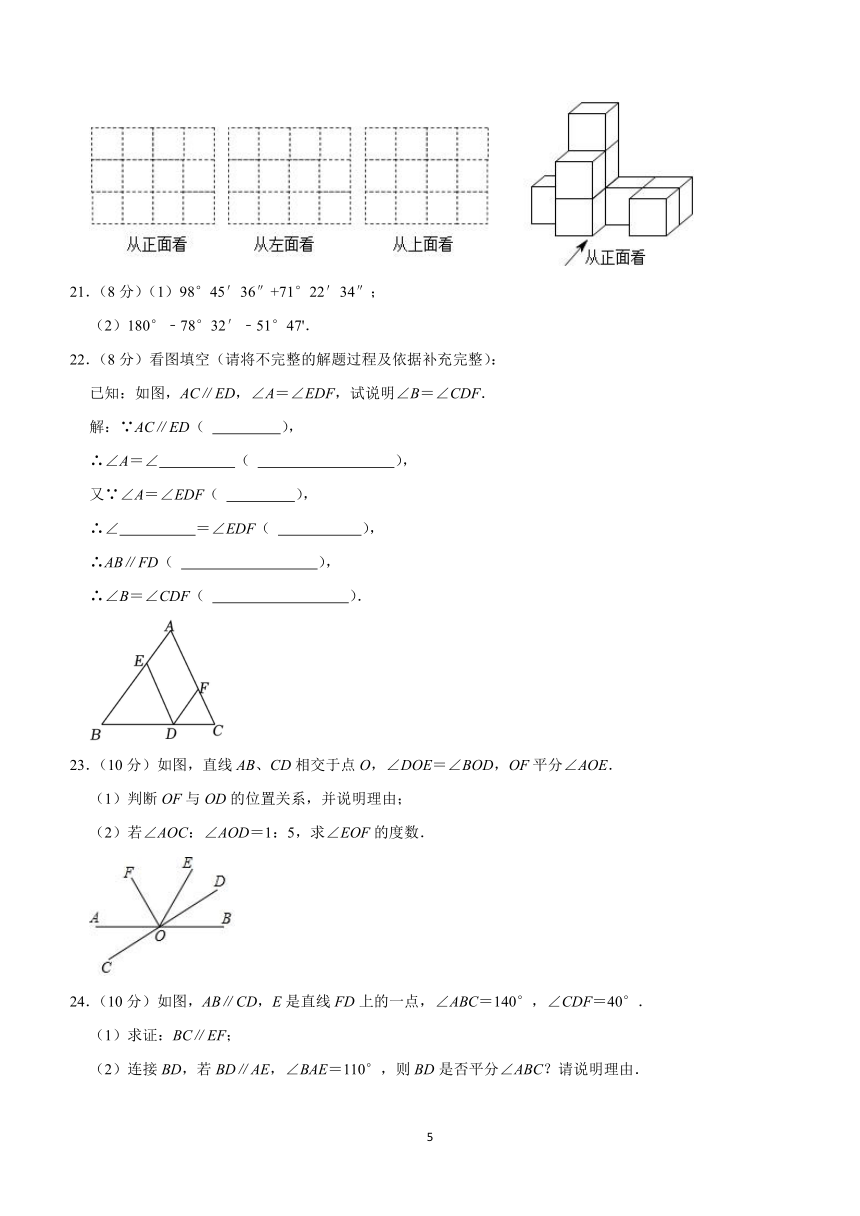
20.(6分)如图,由几个相同的小正方体搭成一个几何体,请画出这个几何体的三种视图.(在所提供的方格内涂上相应的阴影即可)
21.(8分)(1)98°45′36″+71°22′34″;
(2)180°﹣78°32′﹣51°47'.
22.(8分)看图填空(请将不完整的解题过程及依据补充完整):
已知:如图,AC∥ED,∠A=∠EDF,试说明∠B=∠CDF.
解:∵AC∥ED( ),
∴∠A=∠ ( ),
又∵∠A=∠EDF( ),
∴∠ =∠EDF( ),
∴AB∥FD( ),
∴∠B=∠CDF( ).
23.(10分)如图,直线AB、CD相交于点O,∠DOE=∠BOD,OF平分∠AOE.
(1)判断OF与OD的位置关系,并说明理由;
(2)若∠AOC:∠AOD=1:5,求∠EOF的度数.
24.(10分)如图,AB∥CD,E是直线FD上的一点,∠ABC=140°,∠CDF=40°.
(1)求证:BC∥EF;
(2)连接BD,若BD∥AE,∠BAE=110°,则BD是否平分∠ABC?请说明理由.
25.(12分)如图1,直线MN与直线AB、CD分别交于点E、F,∠1与∠2互补.
(1)试判断直线AB与直线CD的位置关系,并说明理由;
(2)如图2,∠BEF与∠EFD的角平分线交于点P,EP与CD交于点G,点H是MN上一点,且GH⊥EG,求证:PF∥GH;
(3)如图3,在(2)的条件下,连接PH,K是GH上一点使∠PHK=∠HPK,作PQ平分∠EPK,问∠HPQ的大小是否发生变化?请判断结论,直接写出答案,不用说明理由.
参考答案与试题解析
一.选择题(共10小题,每题3分,满分30分)
1.(3分)下列所示的图案分别是奔驰、雪铁龙、大众、三菱汽车的车标,其中可以看作由“基本图案”经过平移得到的是( )
A. B. C. D.
【解答】解:根据平移的性质可知:
平移改变方向和距离,
所以B选项可以看作由“基本图案”经过平移得到.
故选:B.
2.(3分)如图是一跳远运动员跳落沙坑时留下的痕迹,P1,P2,P3是三次跳远的落点,则表示该运动员成绩的是( )
A.线段AP1的长 B.线段AP2的长
C.线段BP3的长 D.线段CP3的长
【解答】解:表示该运动员成绩的AP2的长.
故选:B.
3.(3分)如图,将正方体的平面展开图重新折成正方体后,“数”字对面的字是( )
A.喜 B.欢 C.我 D.学
【解答】解:这是一个正方体的平面展开图,共有六个面,其中面“我”与面“学”相对,面“数”与面“喜”相对,面“们”与面“欢”相对.
故选:A.
4.(3分)如图,下列说法错误的是( )
A.∠C与∠1是内错角 B.∠2与∠A是内错角
C.∠A与∠B是同旁内角 D.∠A与∠3是同位角
【解答】解:A、∠C与∠1是内错角,故说法正确;
B、∠2与∠A是同位角,故说法错误;
C、∠A与∠B是同旁内角,故说法正确;
D、∠A与∠3是同位角,故说法正确;
故选:B.
5.(3分)一个正方形的面积是30,估计它的边长的大小在( )
A.3与4之间 B.4与5之间 C.5与6之间 D.6与7之间
【解答】解:∵正方形的面积是30,
∴它的边长为,
∵,
∴它的边长的大小在3和4之间,
故选:A.
6.(3分)下列命题中真命题的个数有( )
(1)过一点有且只有一条直线与已知直线垂直
(2)负数没有算术平方根
(3)两条平行线被第三条直线所截,内错角的平分线互相平行
(4)射线AO和射线OA是同一条射线
(5)若一个角的两边与另一个角的两边平行,则这两个角相等
A.1个 B.2个 C.3个 D.4个
【解答】解:(1)过一点有且只有一条直线与已知直线垂直,真命题;
(2)负数没有算术平方根,真命题;
(3)两条平行线被第三条直线所截,内错角的平分线互相平行,真命题;
(4)射线AO和射线OA不是同一条射线,不是真命题;
(5)若一个角的两边与另一个角的两边平行,则这两个角相等或互补,不是真命题;
所以真命题有3个,
故选:C.
7.(3分)如图,已知线段AB,延长AB至C,使得BC=AB,若D是BC的中点,CD=2cm,则AC的长等于( )
A.4cm B.8cm C.10cm D.12cm
【解答】解:∵D是BC的中点,CD=2cm,
∴BC=2CD=4cm,
∵BC=AB,
∴AB=2BC=8cm,
∴AC=AB+BC=8+4=12cm.
故选:D.
8.(3分)如图,直线AB,CD相交于点O,EO⊥AB,垂足为O,∠AOC=50°,则∠DOE的度数为( )
A.50° B.40° C.30° D.20°
【解答】解:∵EO⊥AB,
∴∠EOA=90°,
∴∠AOC+∠DOE=90°,
∵∠AOC=50°,
∴∠DOE=90°﹣∠AOC=40°,
故选:B.
9.(3分)如图,长方形纸带ABCD中,AB∥CD,将纸带沿EF折叠,A、D两点分别落在A'、D′处,若∠1=62°,则∠2的大小是( )
A.46° B.56° C.62° D.72°
【解答】解:∵AB∥CD,
∴∠AEF=∠1=62°,
由折叠知∠A'EF=∠AEF=62°,
∴∠2=180°﹣∠AEF﹣∠A'EF=56°.
故选:B.
10.(3分)①如图1,AB∥CD,则∠A+∠E+∠C=360°;
②如图2,AB∥CD,则∠P=∠A﹣∠C;
③如图3,AB∥CD,则∠E=∠A+∠1;
④如图4,直线AB∥CD∥EF,点O在直线EF上,则∠α﹣∠β+∠γ=180°.
以上结论正确的个数是( )
A.1个 B.2个 C.3个 D.4个
【解答】解:
①如图1,过点E作直线EF∥AB,
∵AB∥CD,
∴AB∥CD∥EF,
∴∠A+∠1=180°,∠2+∠C=180°,
∴∠A+∠C+∠AEC=360°,
故本结论正确,符合题意;
②如图2,∵∠1是△CEP的外角,
∴∠1=∠C+∠P,
∵AB∥CD,
∴∠A=∠1,
∴∠A=∠C+∠P,
∴∠P=∠A﹣∠C,
故本结论正确,符合题意;
③如图3,过点E作直线EF∥AB,
∵AB∥CD,
∴AB∥CD∥EF,
∴∠A+∠3=180°,∠1=∠2,
∴∠A+∠AEC﹣∠1=180°,
即∠AEC=180°+∠1﹣∠A,
故本结论错误,不符合题意;
④如图4,∵AB∥EF,
∴∠α=∠BOF,
∵CD∥EF,
∴∠γ+∠COF=180°,
∵∠BOF=∠COF+∠β,
∴∠COF=∠α﹣∠β,
∴∠γ+∠α﹣∠β=180°,
故本结论正确,符合题意;
故正确的结论为:①②④.
故选:C.
二.填空题(共8小题,其中11-14每题3分,15-18每题4分,满分28分)
11.(3分)16的算术平方根是 4 .
【解答】解:∵(±4)2=16,
∴16的算术平方根为4,
故答案为:4.
12.(3分)把下列命题写成“如果…那么…”的形式:“对顶角相等”: 如果两个角是对顶角,那么这两个角相等 .
【解答】解:把“对顶角相等”写成“如果…那么…”的形式:如果两个角是对顶角,那么这两个角相等.
故答案为:如果两个角是对顶角,那么这两个角相等.
13.(3分)如图,能用字母表示的以点C为端点的线段的条数为m,能用字母表示的以点C为端点的射线的条数为n,则m﹣n的值为 2 .
【解答】解:由图可得,能用字母表示的以点C为端点的线段的条数m=4,
能用字母表示的以点C为端点的射线的条数n=2,
∴m﹣n的值为2,
故答案为:2.
14.(3分)如图,一把直尺沿直线断开并错位,点E,D,B,F在同一直线上,若∠ADE=125°,则∠DBC的度数为 55° .
【解答】解:∵∠ADE=125°,
∴∠ADB=180°﹣125°=55°,
∵AD∥BC,
∴∠DBC=∠ADB=55°,
故答案为:55°.
15.(4分)如图,给出条件:①∠C=∠BDE;②∠C=∠CAF;③∠B+∠EDG=180°;④∠BAC+∠C=180°,其中能判定AB∥CD的是 ②③④ .(注:填上所有符合条件的序号)
【解答】解:∵∠C=∠BDE,
∴AC∥BG,
故①不符合题意;
∵∠C=∠CAF,
∴AB∥CD,
故②符合题意;
∵∠B+∠EDG=180°,∠BDE+∠EDG=180°,
∴∠B=∠BDE,
∴AB∥CD,
故③符合题意;
∵∠BAC+∠C=180°,
∴AB∥CD,
故④符合题意;
故答案为:②③④.
16.(4分)如图,△ABC以每秒2cm的速度沿着射线BC向右平移,平移2秒后所得图形是△DEF,连接AD,如果AD=2CE,那么BC= 6cm .
【解答】解:∵△ABC以每秒2cm的速度沿着射线BC向右平移,平移2秒后所得图形是△DEF,
∴AD=4cm,AD=BE,
∵AD=2CE,
∴CE=2cm,
∴BC=BE+CE=4+2=6(cm).
故答案为:6cm.
17.(4分)如图摆放的一副学生用直角三角板,∠F=30°,∠C=45°,AB与DE相交于点G,当EF∥BC时,∠EGB的度数是 105° .
【解答】解:过点G作HG∥BC,
∵EF∥BC,
∴GH∥BC∥EF,
∴∠HGB=∠B,∠HGE=∠E,
在Rt△DEF和Rt△ABC中,∠F=30°,∠C=45°,
∴∠E=60°,∠B=45°,
∴∠HGB=∠B=45°,∠HGE=∠E=60°,
∴∠EGB=∠HGE+∠HGB=60°+45°=105°,
故∠EGB的度数是105°,
故答案为:105°.
18.(4分)下面是一个按某种规律排列的数阵:
根据数阵排列的规律,第n(n是整数,且n≥3)行从左向右数第n﹣2个数是 (用含n的代数式表示)
【解答】解:前(n﹣1)行的数据的个数为2+4+6+…+2(n﹣1)=n(n﹣1),
所以,第n(n是整数,且n≥3)行从左到右数第n﹣2个数的被开方数是n(n﹣1)+n﹣2=n2﹣2,
所以,第n(n是整数,且n≥3)行从左到右数第n﹣2个数是.
故答案为:.
三、解答题(共7小题,满分62分)
19.(8分)如图,已知直线l和直线外三点A,B,C,按下列要求画图:
(1)画射线CA,画直线BC;(只画图,不写作法不写结论)
(2)画点A到l的垂线段,垂足为D;(只画图,不写作法不写结论)
(3)过点B作直线l的平行直线m;(只画图,不写作法不写结论)
(4)在直线l上确定出点BE,使得AE+BE最小,理由是 两点之间线段最短 .
【解答】解:(1)如图,射线CA,直线BC即为所求;
(2)如图,线段AD即为所求;
(3)如图,直线m即为所求;
(4)如图,点E即为所求.理由是,两点之间线段最短.
故答案为:两点之间线段最短.
20.(6分)如图,由几个相同的小正方体搭成一个几何体,请画出这个几何体的三种视图.(在所提供的方格内涂上相应的阴影即可)
【解答】解:如图所示:
21.(8分)(1)98°45′36″+71°22′34″;
(2)180°﹣78°32′﹣51°47'.
【解答】解:(1)98°45′36″+71°22′34″
=169°67′70″
=169°68′10″
=170°8′10″;
(2)180°﹣78°32′﹣51°47'
=179°60′﹣78°32′﹣51°47'
=101°28′﹣51°47'
=100°88′﹣51°47'
=49°41′.
22.(8分)看图填空(请将不完整的解题过程及依据补充完整):
已知:如图,AC∥ED,∠A=∠EDF,试说明∠B=∠CDF.
解:∵AC∥ED( 已知 ),
∴∠A=∠ BED ( 两直线平行,同位角相等 ),
又∵∠A=∠EDF( 已知 ),
∴∠ BED =∠EDF( 等量代换 ),
∴AB∥FD( 内错角相等,两直线平行 ),
∴∠B=∠CDF( 两直线平行,同位角相等 ).
【解答】解:∵AC∥ED(已知),
∴∠A=∠BED(两直线平行,同位角相等),
又∵∠A=∠EDF(已知),
∴∠BED=∠EDF(等量代换),
∴AB∥FD(内错角相等,两直线平行),
∴∠B=∠CDF(两直线平行,同位角相等).
23.(10分)如图,直线AB、CD相交于点O,∠DOE=∠BOD,OF平分∠AOE.
(1)判断OF与OD的位置关系,并说明理由;
(2)若∠AOC:∠AOD=1:5,求∠EOF的度数.
【解答】解:(1)OF与OD的位置关系:互相垂直,
理由:∵OF平分∠AOE,
∴∠AOF=∠FOE,
∵∠DOE=∠BOD,
∴∠AOF+∠BOD=∠FOE+∠DOE=×180°=90°,
∴OF与OD的位置关系:互相垂直;
(2)∵∠AOC:∠AOD=1:5,
∴∠AOC=×180°=30°,
∴∠BOD=∠EOD=30°,
∴∠AOE=120°,
∴∠EOF=∠AOE=60°.
24.(10分)如图,AB∥CD,E是直线FD上的一点,∠ABC=140°,∠CDF=40°.
(1)求证:BC∥EF;
(2)连接BD,若BD∥AE,∠BAE=110°,则BD是否平分∠ABC?请说明理由.
【解答】(1)证明:∵AB∥CD,
∴∠ABC+∠BCD=180°,
∵∠ABC=140°,
∴∠BCD=40°,
∵∠CDF=40°,
∴∠BCD=∠CDF,
∴BC∥EF.
(2)解:结论:BD平分∠ABC.
理由:∵AE∥BD,
∴∠BAE+∠ABD=180°,
∵∠BAE=110°,
∴∠ABD=70°,
∵∠ABC=140°,
∴∠ABD=∠DBC=70°,
∴BD平分∠ABC.
25.(12分)如图1,直线MN与直线AB、CD分别交于点E、F,∠1与∠2互补.
(1)试判断直线AB与直线CD的位置关系,并说明理由;
(2)如图2,∠BEF与∠EFD的角平分线交于点P,EP与CD交于点G,点H是MN上一点,且GH⊥EG,求证:PF∥GH;
(3)如图3,在(2)的条件下,连接PH,K是GH上一点使∠PHK=∠HPK,作PQ平分∠EPK,问∠HPQ的大小是否发生变化?请判断结论,直接写出答案,不用说明理由.
【解答】(1)解:AB∥CD,理由如下:
如图1,∵∠1与∠2互补,
∴∠1+∠2=180°,
∵∠1=∠AEF,∠2=∠CFE,
∴∠AEF+∠CFE=180°,
∴AB∥CD;
(2)证明:如图2,由(1)知,AB∥CD,
∴∠BEF+∠EFD=180°,
∵∠BEF与∠EFD的角平分线交于点P,
∴∠FEP+∠EFP=(∠BEF+∠EFD)=90°,
∴∠EPF=90°,即EG⊥PF,
∵GH⊥EG,
∴PF∥GH;
(3)解:∠HPQ的大小不会发生变化,理由如下:
∵∠PHK=∠HPK,
∴∠PKG=2∠HPK,
∵GH⊥EG,
∴∠KPG=90°﹣∠PKG=90°﹣2∠HPK,
∴∠EPK=180°﹣∠KPG=90°+2∠HPK,
∵PQ平分∠EPK,
∴∠QPK=∠EPK=45°+∠HPK,
∴∠HPQ=∠QPK﹣∠HPK=45°,
∴∠HPQ的大小不会发生变化,其值为45°.
一.选择题(共10小题,每题3分,满分30分)
1.(3分)下列所示的图案分别是奔驰、雪铁龙、大众、三菱汽车的车标,其中可以看作由“基本图案”经过平移得到的是( )
A. B. C. D.
2.(3分)如图是一跳远运动员跳落沙坑时留下的痕迹,P1,P2,P3是三次跳远的落点,则表示该运动员成绩的是( )
A.线段AP1的长 B.线段AP2的长
C.线段BP3的长 D.线段CP3的长
3.(3分)如图,将正方体的平面展开图重新折成正方体后,“数”字对面的字是( )
A.喜 B.欢 C.我 D.学
4.(3分)如图,下列说法错误的是( )
A.∠C与∠1是内错角 B.∠2与∠A是内错角
C.∠A与∠B是同旁内角 D.∠A与∠3是同位角
5.(3分)一个正方形的面积是30,估计它的边长的大小在( )
A.3与4之间 B.4与5之间 C.5与6之间 D.6与7之间
6.(3分)下列命题中真命题的个数有( )
(1)过一点有且只有一条直线与已知直线垂直
(2)负数没有算术平方根
(3)两条平行线被第三条直线所截,内错角的平分线互相平行
(4)射线AO和射线OA是同一条射线
(5)若一个角的两边与另一个角的两边平行,则这两个角相等
A.1个 B.2个 C.3个 D.4个
7.(3分)如图,已知线段AB,延长AB至C,使得BC=AB,若D是BC的中点,CD=2cm,则AC的长等于( )
A.4cm B.8cm C.10cm D.12cm
8.(3分)如图,直线AB,CD相交于点O,EO⊥AB,垂足为O,∠AOC=50°,则∠DOE的度数为( )
A.50° B.40° C.30° D.20°
9.(3分)如图,长方形纸带ABCD中,AB∥CD,将纸带沿EF折叠,A、D两点分别落在A'、D′处,若∠1=62°,则∠2的大小是( )
A.46° B.56° C.62° D.72°
10.(3分)①如图1,AB∥CD,则∠A+∠E+∠C=360°;
②如图2,AB∥CD,则∠P=∠A﹣∠C;
③如图3,AB∥CD,则∠E=∠A+∠1;
④如图4,直线AB∥CD∥EF,点O在直线EF上,则∠α﹣∠β+∠γ=180°.
以上结论正确的个数是( )
A.1个 B.2个 C.3个 D.4个
二.填空题(共8小题,其中11-14每题3分,15-18每题4分,满分28分)
11.(3分)16的算术平方根是 .
12.(3分)把下列命题写成“如果…那么…”的形式:“对顶角相等”: .
13.(3分)如图,能用字母表示的以点C为端点的线段的条数为m,能用字母表示的以点C为端点的射线的条数为n,则m﹣n的值为 .
14.(3分)如图,一把直尺沿直线断开并错位,点E,D,B,F在同一直线上,若∠ADE=125°,则∠DBC的度数为 .
15.(4分)如图,给出条件:①∠C=∠BDE;②∠C=∠CAF;③∠B+∠EDG=180°;④∠BAC+∠C=180°,其中能判定AB∥CD的是 .(注:填上所有符合条件的序号)
16.(4分)如图,△ABC以每秒2cm的速度沿着射线BC向右平移,平移2秒后所得图形是△DEF,连接AD,如果AD=2CE,那么BC= .
17.(4分)如图摆放的一副学生用直角三角板,∠F=30°,∠C=45°,AB与DE相交于点G,当EF∥BC时,∠EGB的度数是 .
18.(4分)下面是一个按某种规律排列的数阵:
根据数阵排列的规律,第n(n是整数,且n≥3)行从左向右数第n﹣2个数是 (用含n的代数式表示)
三、解答题(共7小题,满分62分)
19.(8分)如图,已知直线l和直线外三点A,B,C,按下列要求画图:
(1)画射线CA,画直线BC;(只画图,不写作法不写结论)
(2)画点A到l的垂线段,垂足为D;(只画图,不写作法不写结论)
(3)过点B作直线l的平行直线m;(只画图,不写作法不写结论)
(4)在直线l上确定出点BE,使得AE+BE最小,理由是 .
20.(6分)如图,由几个相同的小正方体搭成一个几何体,请画出这个几何体的三种视图.(在所提供的方格内涂上相应的阴影即可)
21.(8分)(1)98°45′36″+71°22′34″;
(2)180°﹣78°32′﹣51°47'.
22.(8分)看图填空(请将不完整的解题过程及依据补充完整):
已知:如图,AC∥ED,∠A=∠EDF,试说明∠B=∠CDF.
解:∵AC∥ED( ),
∴∠A=∠ ( ),
又∵∠A=∠EDF( ),
∴∠ =∠EDF( ),
∴AB∥FD( ),
∴∠B=∠CDF( ).
23.(10分)如图,直线AB、CD相交于点O,∠DOE=∠BOD,OF平分∠AOE.
(1)判断OF与OD的位置关系,并说明理由;
(2)若∠AOC:∠AOD=1:5,求∠EOF的度数.
24.(10分)如图,AB∥CD,E是直线FD上的一点,∠ABC=140°,∠CDF=40°.
(1)求证:BC∥EF;
(2)连接BD,若BD∥AE,∠BAE=110°,则BD是否平分∠ABC?请说明理由.
25.(12分)如图1,直线MN与直线AB、CD分别交于点E、F,∠1与∠2互补.
(1)试判断直线AB与直线CD的位置关系,并说明理由;
(2)如图2,∠BEF与∠EFD的角平分线交于点P,EP与CD交于点G,点H是MN上一点,且GH⊥EG,求证:PF∥GH;
(3)如图3,在(2)的条件下,连接PH,K是GH上一点使∠PHK=∠HPK,作PQ平分∠EPK,问∠HPQ的大小是否发生变化?请判断结论,直接写出答案,不用说明理由.
参考答案与试题解析
一.选择题(共10小题,每题3分,满分30分)
1.(3分)下列所示的图案分别是奔驰、雪铁龙、大众、三菱汽车的车标,其中可以看作由“基本图案”经过平移得到的是( )
A. B. C. D.
【解答】解:根据平移的性质可知:
平移改变方向和距离,
所以B选项可以看作由“基本图案”经过平移得到.
故选:B.
2.(3分)如图是一跳远运动员跳落沙坑时留下的痕迹,P1,P2,P3是三次跳远的落点,则表示该运动员成绩的是( )
A.线段AP1的长 B.线段AP2的长
C.线段BP3的长 D.线段CP3的长
【解答】解:表示该运动员成绩的AP2的长.
故选:B.
3.(3分)如图,将正方体的平面展开图重新折成正方体后,“数”字对面的字是( )
A.喜 B.欢 C.我 D.学
【解答】解:这是一个正方体的平面展开图,共有六个面,其中面“我”与面“学”相对,面“数”与面“喜”相对,面“们”与面“欢”相对.
故选:A.
4.(3分)如图,下列说法错误的是( )
A.∠C与∠1是内错角 B.∠2与∠A是内错角
C.∠A与∠B是同旁内角 D.∠A与∠3是同位角
【解答】解:A、∠C与∠1是内错角,故说法正确;
B、∠2与∠A是同位角,故说法错误;
C、∠A与∠B是同旁内角,故说法正确;
D、∠A与∠3是同位角,故说法正确;
故选:B.
5.(3分)一个正方形的面积是30,估计它的边长的大小在( )
A.3与4之间 B.4与5之间 C.5与6之间 D.6与7之间
【解答】解:∵正方形的面积是30,
∴它的边长为,
∵,
∴它的边长的大小在3和4之间,
故选:A.
6.(3分)下列命题中真命题的个数有( )
(1)过一点有且只有一条直线与已知直线垂直
(2)负数没有算术平方根
(3)两条平行线被第三条直线所截,内错角的平分线互相平行
(4)射线AO和射线OA是同一条射线
(5)若一个角的两边与另一个角的两边平行,则这两个角相等
A.1个 B.2个 C.3个 D.4个
【解答】解:(1)过一点有且只有一条直线与已知直线垂直,真命题;
(2)负数没有算术平方根,真命题;
(3)两条平行线被第三条直线所截,内错角的平分线互相平行,真命题;
(4)射线AO和射线OA不是同一条射线,不是真命题;
(5)若一个角的两边与另一个角的两边平行,则这两个角相等或互补,不是真命题;
所以真命题有3个,
故选:C.
7.(3分)如图,已知线段AB,延长AB至C,使得BC=AB,若D是BC的中点,CD=2cm,则AC的长等于( )
A.4cm B.8cm C.10cm D.12cm
【解答】解:∵D是BC的中点,CD=2cm,
∴BC=2CD=4cm,
∵BC=AB,
∴AB=2BC=8cm,
∴AC=AB+BC=8+4=12cm.
故选:D.
8.(3分)如图,直线AB,CD相交于点O,EO⊥AB,垂足为O,∠AOC=50°,则∠DOE的度数为( )
A.50° B.40° C.30° D.20°
【解答】解:∵EO⊥AB,
∴∠EOA=90°,
∴∠AOC+∠DOE=90°,
∵∠AOC=50°,
∴∠DOE=90°﹣∠AOC=40°,
故选:B.
9.(3分)如图,长方形纸带ABCD中,AB∥CD,将纸带沿EF折叠,A、D两点分别落在A'、D′处,若∠1=62°,则∠2的大小是( )
A.46° B.56° C.62° D.72°
【解答】解:∵AB∥CD,
∴∠AEF=∠1=62°,
由折叠知∠A'EF=∠AEF=62°,
∴∠2=180°﹣∠AEF﹣∠A'EF=56°.
故选:B.
10.(3分)①如图1,AB∥CD,则∠A+∠E+∠C=360°;
②如图2,AB∥CD,则∠P=∠A﹣∠C;
③如图3,AB∥CD,则∠E=∠A+∠1;
④如图4,直线AB∥CD∥EF,点O在直线EF上,则∠α﹣∠β+∠γ=180°.
以上结论正确的个数是( )
A.1个 B.2个 C.3个 D.4个
【解答】解:
①如图1,过点E作直线EF∥AB,
∵AB∥CD,
∴AB∥CD∥EF,
∴∠A+∠1=180°,∠2+∠C=180°,
∴∠A+∠C+∠AEC=360°,
故本结论正确,符合题意;
②如图2,∵∠1是△CEP的外角,
∴∠1=∠C+∠P,
∵AB∥CD,
∴∠A=∠1,
∴∠A=∠C+∠P,
∴∠P=∠A﹣∠C,
故本结论正确,符合题意;
③如图3,过点E作直线EF∥AB,
∵AB∥CD,
∴AB∥CD∥EF,
∴∠A+∠3=180°,∠1=∠2,
∴∠A+∠AEC﹣∠1=180°,
即∠AEC=180°+∠1﹣∠A,
故本结论错误,不符合题意;
④如图4,∵AB∥EF,
∴∠α=∠BOF,
∵CD∥EF,
∴∠γ+∠COF=180°,
∵∠BOF=∠COF+∠β,
∴∠COF=∠α﹣∠β,
∴∠γ+∠α﹣∠β=180°,
故本结论正确,符合题意;
故正确的结论为:①②④.
故选:C.
二.填空题(共8小题,其中11-14每题3分,15-18每题4分,满分28分)
11.(3分)16的算术平方根是 4 .
【解答】解:∵(±4)2=16,
∴16的算术平方根为4,
故答案为:4.
12.(3分)把下列命题写成“如果…那么…”的形式:“对顶角相等”: 如果两个角是对顶角,那么这两个角相等 .
【解答】解:把“对顶角相等”写成“如果…那么…”的形式:如果两个角是对顶角,那么这两个角相等.
故答案为:如果两个角是对顶角,那么这两个角相等.
13.(3分)如图,能用字母表示的以点C为端点的线段的条数为m,能用字母表示的以点C为端点的射线的条数为n,则m﹣n的值为 2 .
【解答】解:由图可得,能用字母表示的以点C为端点的线段的条数m=4,
能用字母表示的以点C为端点的射线的条数n=2,
∴m﹣n的值为2,
故答案为:2.
14.(3分)如图,一把直尺沿直线断开并错位,点E,D,B,F在同一直线上,若∠ADE=125°,则∠DBC的度数为 55° .
【解答】解:∵∠ADE=125°,
∴∠ADB=180°﹣125°=55°,
∵AD∥BC,
∴∠DBC=∠ADB=55°,
故答案为:55°.
15.(4分)如图,给出条件:①∠C=∠BDE;②∠C=∠CAF;③∠B+∠EDG=180°;④∠BAC+∠C=180°,其中能判定AB∥CD的是 ②③④ .(注:填上所有符合条件的序号)
【解答】解:∵∠C=∠BDE,
∴AC∥BG,
故①不符合题意;
∵∠C=∠CAF,
∴AB∥CD,
故②符合题意;
∵∠B+∠EDG=180°,∠BDE+∠EDG=180°,
∴∠B=∠BDE,
∴AB∥CD,
故③符合题意;
∵∠BAC+∠C=180°,
∴AB∥CD,
故④符合题意;
故答案为:②③④.
16.(4分)如图,△ABC以每秒2cm的速度沿着射线BC向右平移,平移2秒后所得图形是△DEF,连接AD,如果AD=2CE,那么BC= 6cm .
【解答】解:∵△ABC以每秒2cm的速度沿着射线BC向右平移,平移2秒后所得图形是△DEF,
∴AD=4cm,AD=BE,
∵AD=2CE,
∴CE=2cm,
∴BC=BE+CE=4+2=6(cm).
故答案为:6cm.
17.(4分)如图摆放的一副学生用直角三角板,∠F=30°,∠C=45°,AB与DE相交于点G,当EF∥BC时,∠EGB的度数是 105° .
【解答】解:过点G作HG∥BC,
∵EF∥BC,
∴GH∥BC∥EF,
∴∠HGB=∠B,∠HGE=∠E,
在Rt△DEF和Rt△ABC中,∠F=30°,∠C=45°,
∴∠E=60°,∠B=45°,
∴∠HGB=∠B=45°,∠HGE=∠E=60°,
∴∠EGB=∠HGE+∠HGB=60°+45°=105°,
故∠EGB的度数是105°,
故答案为:105°.
18.(4分)下面是一个按某种规律排列的数阵:
根据数阵排列的规律,第n(n是整数,且n≥3)行从左向右数第n﹣2个数是 (用含n的代数式表示)
【解答】解:前(n﹣1)行的数据的个数为2+4+6+…+2(n﹣1)=n(n﹣1),
所以,第n(n是整数,且n≥3)行从左到右数第n﹣2个数的被开方数是n(n﹣1)+n﹣2=n2﹣2,
所以,第n(n是整数,且n≥3)行从左到右数第n﹣2个数是.
故答案为:.
三、解答题(共7小题,满分62分)
19.(8分)如图,已知直线l和直线外三点A,B,C,按下列要求画图:
(1)画射线CA,画直线BC;(只画图,不写作法不写结论)
(2)画点A到l的垂线段,垂足为D;(只画图,不写作法不写结论)
(3)过点B作直线l的平行直线m;(只画图,不写作法不写结论)
(4)在直线l上确定出点BE,使得AE+BE最小,理由是 两点之间线段最短 .
【解答】解:(1)如图,射线CA,直线BC即为所求;
(2)如图,线段AD即为所求;
(3)如图,直线m即为所求;
(4)如图,点E即为所求.理由是,两点之间线段最短.
故答案为:两点之间线段最短.
20.(6分)如图,由几个相同的小正方体搭成一个几何体,请画出这个几何体的三种视图.(在所提供的方格内涂上相应的阴影即可)
【解答】解:如图所示:
21.(8分)(1)98°45′36″+71°22′34″;
(2)180°﹣78°32′﹣51°47'.
【解答】解:(1)98°45′36″+71°22′34″
=169°67′70″
=169°68′10″
=170°8′10″;
(2)180°﹣78°32′﹣51°47'
=179°60′﹣78°32′﹣51°47'
=101°28′﹣51°47'
=100°88′﹣51°47'
=49°41′.
22.(8分)看图填空(请将不完整的解题过程及依据补充完整):
已知:如图,AC∥ED,∠A=∠EDF,试说明∠B=∠CDF.
解:∵AC∥ED( 已知 ),
∴∠A=∠ BED ( 两直线平行,同位角相等 ),
又∵∠A=∠EDF( 已知 ),
∴∠ BED =∠EDF( 等量代换 ),
∴AB∥FD( 内错角相等,两直线平行 ),
∴∠B=∠CDF( 两直线平行,同位角相等 ).
【解答】解:∵AC∥ED(已知),
∴∠A=∠BED(两直线平行,同位角相等),
又∵∠A=∠EDF(已知),
∴∠BED=∠EDF(等量代换),
∴AB∥FD(内错角相等,两直线平行),
∴∠B=∠CDF(两直线平行,同位角相等).
23.(10分)如图,直线AB、CD相交于点O,∠DOE=∠BOD,OF平分∠AOE.
(1)判断OF与OD的位置关系,并说明理由;
(2)若∠AOC:∠AOD=1:5,求∠EOF的度数.
【解答】解:(1)OF与OD的位置关系:互相垂直,
理由:∵OF平分∠AOE,
∴∠AOF=∠FOE,
∵∠DOE=∠BOD,
∴∠AOF+∠BOD=∠FOE+∠DOE=×180°=90°,
∴OF与OD的位置关系:互相垂直;
(2)∵∠AOC:∠AOD=1:5,
∴∠AOC=×180°=30°,
∴∠BOD=∠EOD=30°,
∴∠AOE=120°,
∴∠EOF=∠AOE=60°.
24.(10分)如图,AB∥CD,E是直线FD上的一点,∠ABC=140°,∠CDF=40°.
(1)求证:BC∥EF;
(2)连接BD,若BD∥AE,∠BAE=110°,则BD是否平分∠ABC?请说明理由.
【解答】(1)证明:∵AB∥CD,
∴∠ABC+∠BCD=180°,
∵∠ABC=140°,
∴∠BCD=40°,
∵∠CDF=40°,
∴∠BCD=∠CDF,
∴BC∥EF.
(2)解:结论:BD平分∠ABC.
理由:∵AE∥BD,
∴∠BAE+∠ABD=180°,
∵∠BAE=110°,
∴∠ABD=70°,
∵∠ABC=140°,
∴∠ABD=∠DBC=70°,
∴BD平分∠ABC.
25.(12分)如图1,直线MN与直线AB、CD分别交于点E、F,∠1与∠2互补.
(1)试判断直线AB与直线CD的位置关系,并说明理由;
(2)如图2,∠BEF与∠EFD的角平分线交于点P,EP与CD交于点G,点H是MN上一点,且GH⊥EG,求证:PF∥GH;
(3)如图3,在(2)的条件下,连接PH,K是GH上一点使∠PHK=∠HPK,作PQ平分∠EPK,问∠HPQ的大小是否发生变化?请判断结论,直接写出答案,不用说明理由.
【解答】(1)解:AB∥CD,理由如下:
如图1,∵∠1与∠2互补,
∴∠1+∠2=180°,
∵∠1=∠AEF,∠2=∠CFE,
∴∠AEF+∠CFE=180°,
∴AB∥CD;
(2)证明:如图2,由(1)知,AB∥CD,
∴∠BEF+∠EFD=180°,
∵∠BEF与∠EFD的角平分线交于点P,
∴∠FEP+∠EFP=(∠BEF+∠EFD)=90°,
∴∠EPF=90°,即EG⊥PF,
∵GH⊥EG,
∴PF∥GH;
(3)解:∠HPQ的大小不会发生变化,理由如下:
∵∠PHK=∠HPK,
∴∠PKG=2∠HPK,
∵GH⊥EG,
∴∠KPG=90°﹣∠PKG=90°﹣2∠HPK,
∴∠EPK=180°﹣∠KPG=90°+2∠HPK,
∵PQ平分∠EPK,
∴∠QPK=∠EPK=45°+∠HPK,
∴∠HPQ=∠QPK﹣∠HPK=45°,
∴∠HPQ的大小不会发生变化,其值为45°.
同课章节目录
