25.1.1随机事件（41张PPT）

课件41张PPT。
在第二次世界大战中，美国曾经宣布：一名优秀数学家的作用超过10个师的兵力．这句话有一个非同寻常的来历．
1943年以前，在大西洋上英美运输船队常常受到德国潜艇的袭击，当时，英美两国限于实力，无力增派更多的护航舰。一时间，德军的“潜艇战”搞得盟军焦头烂额。
为此，有位美国海军将领专门去请教了一位数学家，数学家们运用概率分析后认为：舰队与敌潜艇相遇是一个随机事件，从数学角度来看这一问题，它具有一定的规律性。一定数量的船（为100艘）编队规模越小，编次就越多（为每次20艘，就要有5个编次）。编次越多，与敌人相遇的概率就越大．
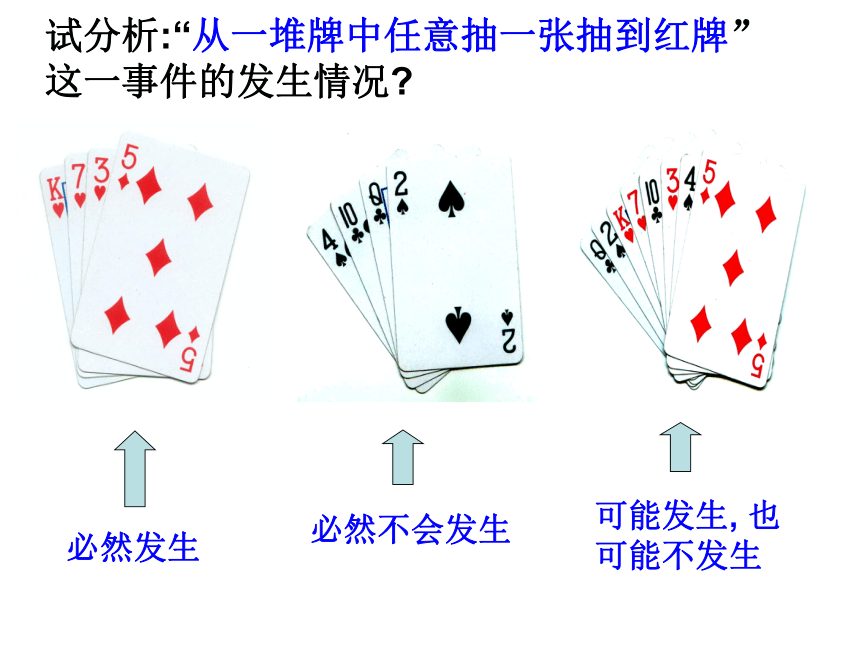
美国海军接受了数学家的建议，命令舰队在指定海域集合，再集体通过危险海域，然后各自驶向预定港口。结果奇迹出现了：盟军舰队遭袭被击沉的概率由原来的25％降为1％，大大减少了损失，保证了物资的及时供应．1名数学家＝10个师天有不测风云 刮风 下雨晴天25.1.1随机事件试分析:“从一堆牌中任意抽一张抽到红牌”这一事件的发生情况?可能发生, 也可能不发生必然发生必然不会发生 在一定条件下重复进行试验时,有的事件在每次试验中必然发生,相反,有的事件在每次试验中都不会发生.而有的事件在试验中有可能发生，也有可能不发生。问：一块铁放入水中，会不会下沉？在一定条件下，必然会发生的事件叫做必然事件。答：铁必然会沉入水中，即100%沉入水中。问：跑一百米只用5秒钟，信不信？答：绝对不可能，即可能性为0。一定条件下，必然不会发生的事件叫做
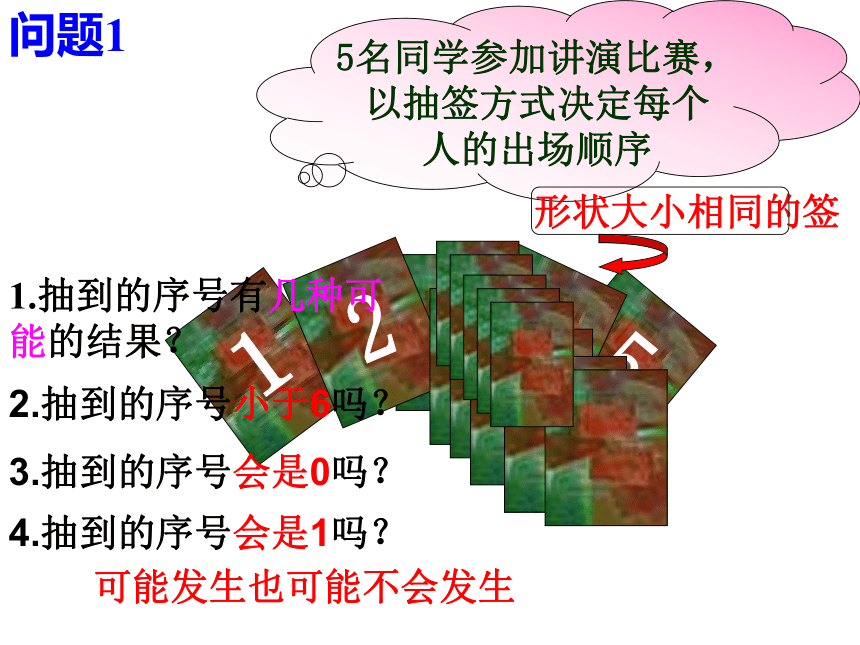
不可能事件。问：买100万张彩票，那么你一定能买到一等奖吗？答：买到一等奖有可能发生，也有可能不发生。在一定条件下，可能发生也可能不发生的事件叫做随机事件。只要功夫深，铁杵磨成针。“拔苗助长”煮熟的鸭子，飞了1、在地球上，太阳每天从东方升起。2、有一匹马奔跑的速度是70千米/秒。3、明天，我买一注体育彩票，得500万大奖。例1　 判断下列事件中哪些是必然事件，哪些是不可能事件，哪些是随机事件？4、用长为3cm、4cm、7cm的三条线段首尾顺次连结，构成一个三角形。5、掷一枚均匀的硬币，正面朝上。6、2015年12月11日当天我县下雨。7.手电简的电池没电，灯炮发亮；8、当x是实数时，x2≥0;5名同学参加讲演比赛，以抽签方式决定每个人的出场顺序1.抽到的序号有几种可能的结果？2.抽到的序号小于6吗？3.抽到的序号会是0吗？4.抽到的序号会是1吗？形状大小相同的签可能发生也可能不会发生问题1我们一起玩①可能出现哪些点数？请考虑以下问题：掷一次骰
子，在骰子向上的一面上：②出现的点数大于0吗？③出现的点数会是7吗？④出现的点数会是4吗？问题2 　　　　　 冠军属于外国选手是不可能事件 冠军属于王楠是随机事件冠军属于中国是必然事件 我国运动员张怡宁、王楠在最后决赛中会师冠军属于中国 冠军属于王楠冠军属于外国选手（5）经过城市中某一有交通信号灯的路口，遇到红灯；（4）度量三角形的内角和，结果是360°；（3）掷一枚骰子，向上的一面是6点；（2）篮球队员在罚线上投篮一次，未投中； 下列事件中，哪些是必然事件，哪些是不可能事件，哪些是随机事件。（1）通常加热到100℃时，水沸腾；必然事件随机事件随机事件不可能事件随机事件世界是你们的,我听你说（6）汽车累积行驶1万公里,从未出现故障。随机事件你能列举一些生活中的随机事件、不可能事件和必然事件的例子吗？ 相传古代有个王国，国王非常阴险而多疑，一位正直的大臣得罪了国王，被叛死刑，这个国家世代沿袭着一条奇特的法规：凡是死囚，在临刑前都要抽一次“生死签”（写着“生”和“死”的两张纸条），犯人当众抽签，若抽到“死”签，则立即处死，若抽到“生”签，则当众赦免。国王一心想处死大臣，与几个心腹密谋，想出一条毒计：嘿嘿,这次非让你死不可!毒计：暗中让执行官把“生死签”上都写成“死”，两死抽一，必死无疑。然而，在断头台前，聪明的大臣迅速抽出一张签纸塞进嘴里，等到执行官反应过来，签纸早已吞下，大臣故作叹息说：“我听天意，将苦果吞下，只要看剩下的签是什么字就清楚了。”剩下的当然写着“死”字，国王怕犯众怒，只好当众释放了大臣。 嘿嘿,这次非让你死不可!嘿嘿,这次非让你死不可!老臣自有妙计！概念巩固思考：（1）在法规中，大臣被处死是什么事件？（2）在国王的阴谋中，大臣被处死是什么事件？（3）在大臣的计策中，大臣被处死是什么事件？
现在有一个盒子，5个红球，4个
白球，每个球除颜色外全部相同。在看不到球的条件下，随机地从袋子中摸出一个球。
问题：
（2）摸出白球和摸出红球的可能性一样大吗？ （1）这个球是白球还是红球？（3）哪种可能性大,为什么?归纳：一般地，随机事件发生的可能性是有大小的，不同的随机事件发生的可能性的大小有可能不同。思考：能否通过改变袋子中某种颜色的球的数量，使“摸出黑球”和“摸出白球”的可能性大小相同？问题3本节课你有什么收获让大家与你分享快乐！ 同学们听过“天有不测风云”这句话吧!它的原意是指刮风、下雨、阴天、晴天这些天气状况很难预料，后来它被引申为：世界上很多事情具有偶然性，人们不能事先判定这些事情是否会发生。 降水概率90%现在概率的应用日益广泛。本章中，我们将学习一些概率初步知识，从而提高对随机事件发生规律的认识。降水概率90% 人们果真对这
类随机事件完全无
法把握、束手无策
吗？不是！随着对
事件发生的可能性
的深入研究，人们
发现许多随机事件
的发生也具有规律
可循的。概率这个
重要的数字概念
正是在研究这些规律中产生的。人们用它描叙事件发生的可能性的大小。例如，天气预报说明天的降水概率为90%，就意味着明天有很大可能下雨。25.1.2概率 在同样条件下，随机事件可能发生，也可能不发生，那么它发生的可能性有多大呢？能否用数值来刻画呢？这是我们下面要讨论的问题。我们从抛掷硬币这个简单问题说起。探究：概率动手试一试：全班4个同学一组，每组同学掷一枚硬币30次，
记录好“正面向上”的次数，
计算出“正面向上”的频率.注意好小组分工哟！抛掷次数n
“正面向上”的频数m“正面向上”的频率随着抛掷次数的增加,“正面向上”
的频率的变化趋势有何规律?仔细看一看nnnm实验结论: 当抛硬币的次数很多时,出现正面向上的频率值是稳定的,接近于常数0.5,在它附近摆动.　　一般地，在大量重复试验中，如果事件Ａ发生的频率稳定在某个常数p附近，那么这个常数p就叫做事件Ａ的概率，记为P(A)=p.事件一般用大写英文字母Ａ，Ｂ，Ｃ，Ｄ．．．表示求概率的方法：通过大量的重复试验，统计出这个事件的频率近似地作为它的概率。例2：对一批衬衫进行抽查，结果如下表：0.880.890.9010.905求抽取一件衬衫是优等品的概率约是多少？抽取衬衫2000件，约有优质品几件？某射手进行射击，结果如下表所示：(1)填表(2)这个射手射击一次，击中靶心的概率是多少？０.５(3)这射手射击1600次，击中靶心的次数是　　。8000.650.580.520.510.5055名同学参加讲演比赛，以抽签方式决定每个人的出场顺序形状大小相同的签以上两个试验具有什么共同特点：1、每一次试验中，可能出现的结果只有有限个。
2、每一次试验中，各种结果出现的可能性相等。具有上述特点的事件称为等可能性事件等可能性事件概率的求法：等可能性事件中总共会出现n种结果，
事件Ａ出现了m种结果，则P(A)=因为m. n满足0≦ m ≦ n ，所以0 ≦ m/n ≦ 1 ，小组议一议：p的取值范围　因此0≤P(A) ≤1.
必然事件的概率是1，
不可能事件的概率是0.练习拓展1. 抛掷一个骰子，它落地时
（1）向上的点数为1的概率是多少？（2）向上点数不超过4的概率是多少？
2.有三张牌，抽到Ｊ的概率是０.22，抽到Ｑ的概率是０.38,则抽到Ｋ的概率是　　 0.43.一次抽奖活动中，印发奖券10 000张，其中一等奖一名,奖金5000元，那么第一位抽奖者，（仅买一张）中奖概率为————。课堂小结：1、必然事件Ａ，则Ｐ（Ａ）＝１；
　　不可能事件Ｂ，则Ｐ（Ｂ）＝０；
　　随机事件Ｃ，则０＜Ｐ（Ｃ）＜１。2、求概率的方法：通过大量反复试验，统计出这件事发生的频率近似地做为它的概率。3、等可能事件的概率简单求法。