江苏省无锡市锡东高级中学2023-2024学年高一下学期5月月考数学试卷(含解析)
文档属性
| 名称 | 江苏省无锡市锡东高级中学2023-2024学年高一下学期5月月考数学试卷(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-26 10:38:13 | ||
图片预览




文档简介
2023-2024学年度第二学期5月阶段性考试
高一数学试卷
一、单项选择题:本小题共8题,每小题5分,共40分。在每小题给出的四个选项中,只有一个选项是符合题目要求的。
1.用斜二测画法画一个水平放置的平面图形的直观图为如图所示的等腰三角形,其中,则原平面图形的面积为( )
A.1 B. C. D.2
2.在中,,,,则这个三角形的面积是( )
A. B. C. D.1
3.已知向量,,若与共线,则实数的值为( )
A. B.1 C. D.0
4.已知α、β是平面,m、n是直线,下列命题中不正确的是( )
A.若,,则 B.若,,则
C.若,,则 D.若,,则
5.某高校12名毕业生的起始月薪如下表所示:
毕业生 1 2 3 4 5 6 7 8 9 10 11 12
起始月薪 2850 2950 3050 2880 2755 2710 2890 3130 2940 3325 2920 2880
则第85百分位数是( )
A.3325 B.3130 C.3050 D.2950
6.如图,某登山队在山脚A处测得山顶B的仰角为,沿倾斜角为的斜坡前进若干米后到达D处,又测得山顶的仰角为,已知山的高度BC为1千米,则该登山队从A到D前进了( )
A.千米 B.千米 C.1千米 D.1.5千米
7.在中,已知边上的两条中线相交于点,则( )
A. B. C. D.
8.设内角,,所对的边分别为,,.若,,则面积的最大值为( )
A. B. C. D.3
二、选择题:本题共3小题,每小题6分,共18分。在每小题给出的选项中,有多项符合题目要求。全部选对的得6分,部分选对的得部分分,有选错的得0分。
9.正方体中,下列叙述正确的有( )
A.直线与所成角为
B.直线与所成角为
C.直线与平面所成角为
D.直线与平面所成角为
10.给定一组数5,5,4,3,3,3,2,2,2,1,则( )
A.平均数为3 B.标准差为
C.众数为2 D.85%分位数为5
11.在中,角、、所对的边分别为、、,且,则下列说法正确的是( )
A.
B.若,则面积的最大值为
C.若,且只有一解,则的取值范围为
D.为的外心,则
三、填空题:本题共3小题,每小题5分,共15分。
12.下表是关于某校高一年级男女生选科意向的调查数据,人数如表所示:
选修物理 选修历史
男生 160 40
女生 80 120
现要在所有参与调查的人中用分层抽样的方法抽取n个人做进一步的调查,若在“选修物理的男生”中抽取了8人,则n的值为 .
13.已知直三棱柱中,,,,其外接球的表面积为,则该三棱柱的侧棱长为 .
14.已知平面向量,满足,与的夹角为,记,则的取值范围为 .
四、解答题:本题共5小题,共77分。解答应写出文字说明、证明过程或演算步骤。
15.如图,在三棱柱中,平面平面,侧面是矩形,点E,F分别为,的中点.求证:
(1);
(2)平面.
16.平面直角坐标系中,为坐标原点,已知,为两个夹角成的单位向量,,.
(1)求;
(2)设,问是否存在实数,使得是以为斜边的直角三角形?若存在,求的值;若不存在,请说明理由.
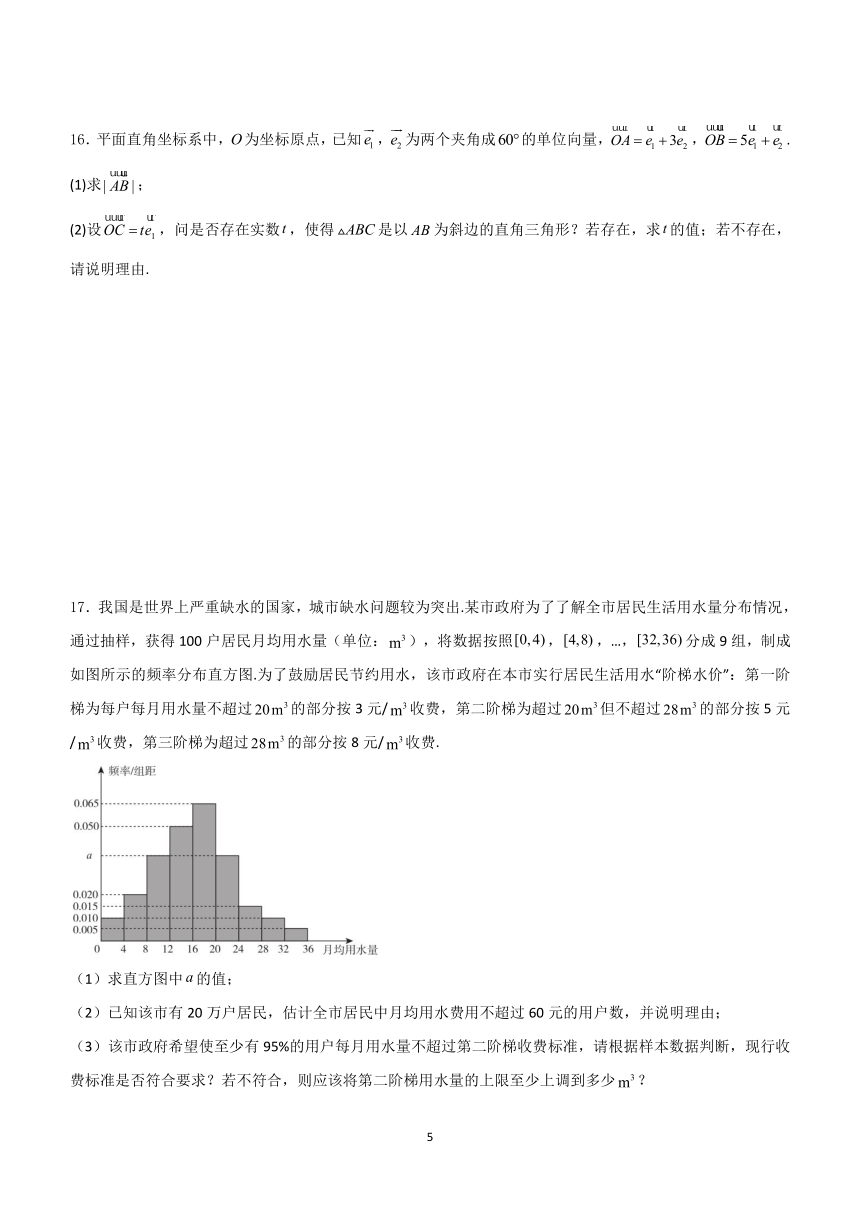
17.我国是世界上严重缺水的国家,城市缺水问题较为突出.某市政府为了了解全市居民生活用水量分布情况,通过抽样,获得100户居民月均用水量(单位:),将数据按照,,…,分成9组,制成如图所示的频率分布直方图.为了鼓励居民节约用水,该市政府在本市实行居民生活用水“阶梯水价”:第一阶梯为每户每月用水量不超过的部分按3元/收费,第二阶梯为超过但不超过的部分按5元/收费,第三阶梯为超过的部分按8元/收费.
(1)求直方图中的值;
(2)已知该市有20万户居民,估计全市居民中月均用水费用不超过60元的用户数,并说明理由;
(3)该市政府希望使至少有95%的用户每月用水量不超过第二阶梯收费标准,请根据样本数据判断,现行收费标准是否符合要求?若不符合,则应该将第二阶梯用水量的上限至少上调到多少?
18.在中,角,,的对边分别为,,,已知,且,.
(1)求证:;
(2)求的面积.
19.《几何原本》是古希腊数学家欧几里得创作的一部传世巨著,该书以基本定义、公设和公理作为推理的出发点,第一次实现了几何学的系绕化、条理化,成为用公理化方法建立数学演绎体系的最早典范.书中第Ⅰ卷第47号命题是著名的毕达哥拉斯(勾股定理),证明过程中以直角三角形中的各边为边分别向外作了正方形(如图1).某校数学兴趣小组对上述图形结构作拓广探究,提出了如下问题,请帮忙解答.
问题:如图2,已知满足,,设(),四边形、四边形、四边形都是正方形.
(1)当时,求的长度;
(2)求长度的最大值.
2023-2024学年度第二学期5月阶段性考试
高一数学试卷答案解析
一、单项选择题:本小题共8题,每小题5分,共40分。在每小题给出的四个选项中,只有一个选项是符合题目要求的。
1.用斜二测画法画一个水平放置的平面图形的直观图为如图所示的等腰三角形,其中,则原平面图形的面积为( )
A.1 B. C. D.2
【答案】A
【解析】还原后的图形可知OB=2,OA=1,所以面积为
2.在中,,,,则这个三角形的面积是( )
A. B. C. D.1
【答案】D
【解析】因为在中,,,,所以.故选:D.
3.已知向量,,若与共线,则实数的值为( )
A. B.1 C. D.0
【答案】C
【解析】由已知,,
又与共线,所以,解得.
4.已知α、β是平面,m、n是直线,下列命题中不正确的是( )
A.若,,则 B.若,,则
C.若,,则 D.若,,则
【答案】A
【解析】对于A,若,,则或者相交或者异面,A错误,
对于B,若,,则,B正确,
对于C,若,,则,C正确,
对于D,若,,则,D正确,
5.某高校12名毕业生的起始月薪如下表所示:
毕业生 1 2 3 4 5 6 7 8 9 10 11 12
起始月薪 2850 2950 3050 2880 2755 2710 2890 3130 2940 3325 2920 2880
则第85百分位数是( )
A.3325 B.3130 C.3050 D.2950
【答案】B
【解析】将这12个数从小到大的顺序排列:2710,2755,2850,2880,2880,2890, 2920,2940,2950,3050,3130,3325.
又因为第,所以第第85百分位数是第11个数据,为3130.
6.如图,某登山队在山脚A处测得山顶B的仰角为,沿倾斜角为的斜坡前进若干米后到达D处,又测得山顶的仰角为,已知山的高度BC为1千米,则该登山队从A到D前进了( )
A.千米 B.千米 C.1千米 D.1.5千米
【答案】C
【解析】如图,过D作交于点,交于点,
由题意得则
在D处测得山顶的仰角为, 即,,则
设,在中由正弦定理得:
,
,因为,即,即从A到D前进了1千米,
7.在中,已知边上的两条中线相交于点,则( )
A. B. C. D.
【答案】B
【解析】解:因为所以,所以,
又因为,所以三角形为直角三角,
建立如图所示的坐标系,则,
因为分别为中点,所以,所以,,
所以==.
8.设内角,,所对的边分别为,,.若,,则面积的最大值为( )
A. B. C. D.3
【答案】B
【解析】因为,所以由正弦定理可得,得,
由余弦定理得,,
所以,当且仅当时取等号,所以,
所以,所以,当且仅当时取等号,
所以面积的最大值为,
二、选择题:本题共3小题,每小题6分,共18分。在每小题给出的选项中,有多项符合题目要求。全部选对的得6分,部分选对的得部分分,有选错的得0分。
9.正方体中,下列叙述正确的有( )
A.直线与所成角为
B.直线与所成角为
C.直线与平面所成角为
D.直线与平面所成角为
【答案】AB
【解析】在正方体ABCD - A1B1C1D1中,由BC∥A1D1,BC = A1D1 可得四边形BCD1A1为平行四边形,
则A1 B∥D1C,则∠B1CD1为直线A1B与B1C所成角,
连接B1D1,可得△BCD1为等边三角形,
则直线A1B与B1C所成角为60°,A正确;
在正方体ABCD - A1B1C1D1中,A1D1⊥平面CC1D1D,
则A1D1⊥C1D,而C1D⊥DC1,A1D1∩D1C = D1,∴C1D⊥平面A1CD1则C1D⊥A1C,B正确;
∵AA1⊥底面ABCD,∴∠A1CA为直线 A1C与平面ABCD所成角,
在Rt△A1AC中,∵AA1∵A1B1⊥平面BCC1B1,∴∠A1BB1为直线A1B与平面BCC1B1所成角,为45°,D错误.
10.给定一组数5,5,4,3,3,3,2,2,2,1,则( )
A.平均数为3 B.标准差为
C.众数为2 D.85%分位数为5
【答案】AD
【解析】由平均数的计算公式,可得,A正确;
由方程的公式,可得,
所以标准差为,B错误;
由众数的定义,可得数据的众数为2和3,C错误;
将数据从小到大排序得1,2,2,2,3,3,3,4,5,5,可得,所以第85百分位数为5,D正确.
11.在中,角、、所对的边分别为、、,且,则下列说法正确的是( )
A.
B.若,则面积的最大值为
C.若,且只有一解,则的取值范围为
D.为的外心,则
【答案】ABD
【解析】因为,由正弦定理可得
因为,所以,所以,A正确;
若,且,所以,
由余弦定理得,
由,可得,当且仅当时,等号成立,所以,
则面积,所以面积的最大值为,B正确;
若,且,由正弦定理得,可得所以,
当时,可得,所以时有一解,C错误;
对于D中,如图所示,作交于点点,则点为的中点,且,
设,所以,
所以,D正确.
三、填空题:本题共3小题,每小题5分,共15分。
12.下表是关于某校高一年级男女生选科意向的调查数据,人数如表所示:
选修物理 选修历史
男生 160 40
女生 80 120
现要在所有参与调查的人中用分层抽样的方法抽取n个人做进一步的调查,若在“选修物理的男生”中抽取了8人,则n的值为 .
【答案】20
【解析】根据分层抽样方法得:,解得.
13.已知直三棱柱中,,,,其外接球的表面积为,则该三棱柱的侧棱长为 .
【答案】2
【解析】由题意,该直三棱柱可补形为长方体,
则长方体的外接球即是直三棱柱的外接球.
所以体对角线的长为球的直径,设球的半径为,则.所以
设侧棱为,则,解得,即侧棱为2.
14.已知平面向量,满足,与的夹角为,记,则的取值范围为 .
【答案】
【解析】因为平面向量,满足,与的夹角为,
设,,,
则,所以,,
,、、三点共线,
又到直线的距离,,即的取值范围为.
四、解答题:本题共5小题,共77分。解答应写出文字说明、证明过程或演算步骤。
15.如图,在三棱柱中,平面平面,侧面是矩形,点E,F分别为,的中点.求证:
(1);
(2)平面.
【解析】(1)因为侧面是矩形,所以,
因为平面平面,平面平面,在平面内,
所以平面,
因为在平面内,所以;
(2)取的中点,连结,,
在△中,,分别是,的中点,
所以,且,
在矩形中,是的中点,
所以,且,
所以,且,
所以四边形为平行四边形,所以,
又因为在平面外,在平面内,
所以平面.
16.平面直角坐标系中,为坐标原点,已知,为两个夹角成的单位向量,,.
(1)求;
(2)设,问是否存在实数,使得是以为斜边的直角三角形?若存在,求的值;若不存在,请说明理由.
【答案】(1) ; (2)存在,
【解析】(1),
.
(2),,
若是以为斜边的直角三角形,则,
,
化简得:,解得. 存在满足条件.
17.我国是世界上严重缺水的国家,城市缺水问题较为突出.某市政府为了了解全市居民生活用水量分布情况,通过抽样,获得100户居民月均用水量(单位:),将数据按照,,…,分成9组,制成如图所示的频率分布直方图.为了鼓励居民节约用水,该市政府在本市实行居民生活用水“阶梯水价”:第一阶梯为每户每月用水量不超过的部分按3元/收费,第二阶梯为超过但不超过的部分按5元/收费,第三阶梯为超过的部分按8元/收费.
(1)求直方图中的值;
(2)已知该市有20万户居民,估计全市居民中月均用水费用不超过60元的用户数,并说明理由;
(3)该市政府希望使至少有95%的用户每月用水量不超过第二阶梯收费标准,请根据样本数据判断,现行收费标准是否符合要求?若不符合,则应该将第二阶梯用水量的上限至少上调到多少?
【答案】(1);(2),理由见解析
(3)现行收费标准不符合要求,需将第二阶梯用水量的上限至少上调到
【解析】(1)由频率分布直方图可得
,解得.
(2)由“阶梯水价”知“用户月均用水费用不超过60元即“用户月均用水不超过”,则100户居民中有,由此可以估计全市7320万户居民中月均用水费用不超过60元的用户数为.
(3)抽取的100户居民月均用水量不超过的频率为:
,
,所以现行收费标准不符合要求.
抽取的100户居民月均用水量不超过的频率为:
,
,
现行收费标准不符合要求,需将第二阶梯用水量的上限至少上调到.
18.在中,角,,的对边分别为,,,已知,且,.
(1)求证:;
(2)求的面积.
【答案】(1)证明见解析 ; (2)
【解析】(1)证明:,,所以,
根据正弦定理得,,
又所以,即
(2)由余弦定理得,
由(1),得,结合可得.
即,解得或 (舍去),所以
19.《几何原本》是古希腊数学家欧几里得创作的一部传世巨著,该书以基本定义、公设和公理作为推理的出发点,第一次实现了几何学的系绕化、条理化,成为用公理化方法建立数学演绎体系的最早典范.书中第Ⅰ卷第47号命题是著名的毕达哥拉斯(勾股定理),证明过程中以直角三角形中的各边为边分别向外作了正方形(如图1).某校数学兴趣小组对上述图形结构作拓广探究,提出了如下问题,请帮忙解答.
问题:如图2,已知满足,,设(),四边形、四边形、四边形都是正方形.
(1)当时,求的长度;
(2)求长度的最大值.
【答案】(1)6 ; (2)6
【解析】(1)在中,,,,则,,
因为,所以
在中,,,
由余弦定理
所以的长度为.
(2)在中,由余弦定理得,所以,
设,在中,由余弦定理得,
所以 ①
在中,由正弦定理得,
所以,
代入①可得,
因为,
所以,
当即时,的最大值为,
所以长度的最大值为6.
高一数学试卷
一、单项选择题:本小题共8题,每小题5分,共40分。在每小题给出的四个选项中,只有一个选项是符合题目要求的。
1.用斜二测画法画一个水平放置的平面图形的直观图为如图所示的等腰三角形,其中,则原平面图形的面积为( )
A.1 B. C. D.2
2.在中,,,,则这个三角形的面积是( )
A. B. C. D.1
3.已知向量,,若与共线,则实数的值为( )
A. B.1 C. D.0
4.已知α、β是平面,m、n是直线,下列命题中不正确的是( )
A.若,,则 B.若,,则
C.若,,则 D.若,,则
5.某高校12名毕业生的起始月薪如下表所示:
毕业生 1 2 3 4 5 6 7 8 9 10 11 12
起始月薪 2850 2950 3050 2880 2755 2710 2890 3130 2940 3325 2920 2880
则第85百分位数是( )
A.3325 B.3130 C.3050 D.2950
6.如图,某登山队在山脚A处测得山顶B的仰角为,沿倾斜角为的斜坡前进若干米后到达D处,又测得山顶的仰角为,已知山的高度BC为1千米,则该登山队从A到D前进了( )
A.千米 B.千米 C.1千米 D.1.5千米
7.在中,已知边上的两条中线相交于点,则( )
A. B. C. D.
8.设内角,,所对的边分别为,,.若,,则面积的最大值为( )
A. B. C. D.3
二、选择题:本题共3小题,每小题6分,共18分。在每小题给出的选项中,有多项符合题目要求。全部选对的得6分,部分选对的得部分分,有选错的得0分。
9.正方体中,下列叙述正确的有( )
A.直线与所成角为
B.直线与所成角为
C.直线与平面所成角为
D.直线与平面所成角为
10.给定一组数5,5,4,3,3,3,2,2,2,1,则( )
A.平均数为3 B.标准差为
C.众数为2 D.85%分位数为5
11.在中,角、、所对的边分别为、、,且,则下列说法正确的是( )
A.
B.若,则面积的最大值为
C.若,且只有一解,则的取值范围为
D.为的外心,则
三、填空题:本题共3小题,每小题5分,共15分。
12.下表是关于某校高一年级男女生选科意向的调查数据,人数如表所示:
选修物理 选修历史
男生 160 40
女生 80 120
现要在所有参与调查的人中用分层抽样的方法抽取n个人做进一步的调查,若在“选修物理的男生”中抽取了8人,则n的值为 .
13.已知直三棱柱中,,,,其外接球的表面积为,则该三棱柱的侧棱长为 .
14.已知平面向量,满足,与的夹角为,记,则的取值范围为 .
四、解答题:本题共5小题,共77分。解答应写出文字说明、证明过程或演算步骤。
15.如图,在三棱柱中,平面平面,侧面是矩形,点E,F分别为,的中点.求证:
(1);
(2)平面.
16.平面直角坐标系中,为坐标原点,已知,为两个夹角成的单位向量,,.
(1)求;
(2)设,问是否存在实数,使得是以为斜边的直角三角形?若存在,求的值;若不存在,请说明理由.
17.我国是世界上严重缺水的国家,城市缺水问题较为突出.某市政府为了了解全市居民生活用水量分布情况,通过抽样,获得100户居民月均用水量(单位:),将数据按照,,…,分成9组,制成如图所示的频率分布直方图.为了鼓励居民节约用水,该市政府在本市实行居民生活用水“阶梯水价”:第一阶梯为每户每月用水量不超过的部分按3元/收费,第二阶梯为超过但不超过的部分按5元/收费,第三阶梯为超过的部分按8元/收费.
(1)求直方图中的值;
(2)已知该市有20万户居民,估计全市居民中月均用水费用不超过60元的用户数,并说明理由;
(3)该市政府希望使至少有95%的用户每月用水量不超过第二阶梯收费标准,请根据样本数据判断,现行收费标准是否符合要求?若不符合,则应该将第二阶梯用水量的上限至少上调到多少?
18.在中,角,,的对边分别为,,,已知,且,.
(1)求证:;
(2)求的面积.
19.《几何原本》是古希腊数学家欧几里得创作的一部传世巨著,该书以基本定义、公设和公理作为推理的出发点,第一次实现了几何学的系绕化、条理化,成为用公理化方法建立数学演绎体系的最早典范.书中第Ⅰ卷第47号命题是著名的毕达哥拉斯(勾股定理),证明过程中以直角三角形中的各边为边分别向外作了正方形(如图1).某校数学兴趣小组对上述图形结构作拓广探究,提出了如下问题,请帮忙解答.
问题:如图2,已知满足,,设(),四边形、四边形、四边形都是正方形.
(1)当时,求的长度;
(2)求长度的最大值.
2023-2024学年度第二学期5月阶段性考试
高一数学试卷答案解析
一、单项选择题:本小题共8题,每小题5分,共40分。在每小题给出的四个选项中,只有一个选项是符合题目要求的。
1.用斜二测画法画一个水平放置的平面图形的直观图为如图所示的等腰三角形,其中,则原平面图形的面积为( )
A.1 B. C. D.2
【答案】A
【解析】还原后的图形可知OB=2,OA=1,所以面积为
2.在中,,,,则这个三角形的面积是( )
A. B. C. D.1
【答案】D
【解析】因为在中,,,,所以.故选:D.
3.已知向量,,若与共线,则实数的值为( )
A. B.1 C. D.0
【答案】C
【解析】由已知,,
又与共线,所以,解得.
4.已知α、β是平面,m、n是直线,下列命题中不正确的是( )
A.若,,则 B.若,,则
C.若,,则 D.若,,则
【答案】A
【解析】对于A,若,,则或者相交或者异面,A错误,
对于B,若,,则,B正确,
对于C,若,,则,C正确,
对于D,若,,则,D正确,
5.某高校12名毕业生的起始月薪如下表所示:
毕业生 1 2 3 4 5 6 7 8 9 10 11 12
起始月薪 2850 2950 3050 2880 2755 2710 2890 3130 2940 3325 2920 2880
则第85百分位数是( )
A.3325 B.3130 C.3050 D.2950
【答案】B
【解析】将这12个数从小到大的顺序排列:2710,2755,2850,2880,2880,2890, 2920,2940,2950,3050,3130,3325.
又因为第,所以第第85百分位数是第11个数据,为3130.
6.如图,某登山队在山脚A处测得山顶B的仰角为,沿倾斜角为的斜坡前进若干米后到达D处,又测得山顶的仰角为,已知山的高度BC为1千米,则该登山队从A到D前进了( )
A.千米 B.千米 C.1千米 D.1.5千米
【答案】C
【解析】如图,过D作交于点,交于点,
由题意得则
在D处测得山顶的仰角为, 即,,则
设,在中由正弦定理得:
,
,因为,即,即从A到D前进了1千米,
7.在中,已知边上的两条中线相交于点,则( )
A. B. C. D.
【答案】B
【解析】解:因为所以,所以,
又因为,所以三角形为直角三角,
建立如图所示的坐标系,则,
因为分别为中点,所以,所以,,
所以==.
8.设内角,,所对的边分别为,,.若,,则面积的最大值为( )
A. B. C. D.3
【答案】B
【解析】因为,所以由正弦定理可得,得,
由余弦定理得,,
所以,当且仅当时取等号,所以,
所以,所以,当且仅当时取等号,
所以面积的最大值为,
二、选择题:本题共3小题,每小题6分,共18分。在每小题给出的选项中,有多项符合题目要求。全部选对的得6分,部分选对的得部分分,有选错的得0分。
9.正方体中,下列叙述正确的有( )
A.直线与所成角为
B.直线与所成角为
C.直线与平面所成角为
D.直线与平面所成角为
【答案】AB
【解析】在正方体ABCD - A1B1C1D1中,由BC∥A1D1,BC = A1D1 可得四边形BCD1A1为平行四边形,
则A1 B∥D1C,则∠B1CD1为直线A1B与B1C所成角,
连接B1D1,可得△BCD1为等边三角形,
则直线A1B与B1C所成角为60°,A正确;
在正方体ABCD - A1B1C1D1中,A1D1⊥平面CC1D1D,
则A1D1⊥C1D,而C1D⊥DC1,A1D1∩D1C = D1,∴C1D⊥平面A1CD1则C1D⊥A1C,B正确;
∵AA1⊥底面ABCD,∴∠A1CA为直线 A1C与平面ABCD所成角,
在Rt△A1AC中,∵AA1
10.给定一组数5,5,4,3,3,3,2,2,2,1,则( )
A.平均数为3 B.标准差为
C.众数为2 D.85%分位数为5
【答案】AD
【解析】由平均数的计算公式,可得,A正确;
由方程的公式,可得,
所以标准差为,B错误;
由众数的定义,可得数据的众数为2和3,C错误;
将数据从小到大排序得1,2,2,2,3,3,3,4,5,5,可得,所以第85百分位数为5,D正确.
11.在中,角、、所对的边分别为、、,且,则下列说法正确的是( )
A.
B.若,则面积的最大值为
C.若,且只有一解,则的取值范围为
D.为的外心,则
【答案】ABD
【解析】因为,由正弦定理可得
因为,所以,所以,A正确;
若,且,所以,
由余弦定理得,
由,可得,当且仅当时,等号成立,所以,
则面积,所以面积的最大值为,B正确;
若,且,由正弦定理得,可得所以,
当时,可得,所以时有一解,C错误;
对于D中,如图所示,作交于点点,则点为的中点,且,
设,所以,
所以,D正确.
三、填空题:本题共3小题,每小题5分,共15分。
12.下表是关于某校高一年级男女生选科意向的调查数据,人数如表所示:
选修物理 选修历史
男生 160 40
女生 80 120
现要在所有参与调查的人中用分层抽样的方法抽取n个人做进一步的调查,若在“选修物理的男生”中抽取了8人,则n的值为 .
【答案】20
【解析】根据分层抽样方法得:,解得.
13.已知直三棱柱中,,,,其外接球的表面积为,则该三棱柱的侧棱长为 .
【答案】2
【解析】由题意,该直三棱柱可补形为长方体,
则长方体的外接球即是直三棱柱的外接球.
所以体对角线的长为球的直径,设球的半径为,则.所以
设侧棱为,则,解得,即侧棱为2.
14.已知平面向量,满足,与的夹角为,记,则的取值范围为 .
【答案】
【解析】因为平面向量,满足,与的夹角为,
设,,,
则,所以,,
,、、三点共线,
又到直线的距离,,即的取值范围为.
四、解答题:本题共5小题,共77分。解答应写出文字说明、证明过程或演算步骤。
15.如图,在三棱柱中,平面平面,侧面是矩形,点E,F分别为,的中点.求证:
(1);
(2)平面.
【解析】(1)因为侧面是矩形,所以,
因为平面平面,平面平面,在平面内,
所以平面,
因为在平面内,所以;
(2)取的中点,连结,,
在△中,,分别是,的中点,
所以,且,
在矩形中,是的中点,
所以,且,
所以,且,
所以四边形为平行四边形,所以,
又因为在平面外,在平面内,
所以平面.
16.平面直角坐标系中,为坐标原点,已知,为两个夹角成的单位向量,,.
(1)求;
(2)设,问是否存在实数,使得是以为斜边的直角三角形?若存在,求的值;若不存在,请说明理由.
【答案】(1) ; (2)存在,
【解析】(1),
.
(2),,
若是以为斜边的直角三角形,则,
,
化简得:,解得. 存在满足条件.
17.我国是世界上严重缺水的国家,城市缺水问题较为突出.某市政府为了了解全市居民生活用水量分布情况,通过抽样,获得100户居民月均用水量(单位:),将数据按照,,…,分成9组,制成如图所示的频率分布直方图.为了鼓励居民节约用水,该市政府在本市实行居民生活用水“阶梯水价”:第一阶梯为每户每月用水量不超过的部分按3元/收费,第二阶梯为超过但不超过的部分按5元/收费,第三阶梯为超过的部分按8元/收费.
(1)求直方图中的值;
(2)已知该市有20万户居民,估计全市居民中月均用水费用不超过60元的用户数,并说明理由;
(3)该市政府希望使至少有95%的用户每月用水量不超过第二阶梯收费标准,请根据样本数据判断,现行收费标准是否符合要求?若不符合,则应该将第二阶梯用水量的上限至少上调到多少?
【答案】(1);(2),理由见解析
(3)现行收费标准不符合要求,需将第二阶梯用水量的上限至少上调到
【解析】(1)由频率分布直方图可得
,解得.
(2)由“阶梯水价”知“用户月均用水费用不超过60元即“用户月均用水不超过”,则100户居民中有,由此可以估计全市7320万户居民中月均用水费用不超过60元的用户数为.
(3)抽取的100户居民月均用水量不超过的频率为:
,
,所以现行收费标准不符合要求.
抽取的100户居民月均用水量不超过的频率为:
,
,
现行收费标准不符合要求,需将第二阶梯用水量的上限至少上调到.
18.在中,角,,的对边分别为,,,已知,且,.
(1)求证:;
(2)求的面积.
【答案】(1)证明见解析 ; (2)
【解析】(1)证明:,,所以,
根据正弦定理得,,
又所以,即
(2)由余弦定理得,
由(1),得,结合可得.
即,解得或 (舍去),所以
19.《几何原本》是古希腊数学家欧几里得创作的一部传世巨著,该书以基本定义、公设和公理作为推理的出发点,第一次实现了几何学的系绕化、条理化,成为用公理化方法建立数学演绎体系的最早典范.书中第Ⅰ卷第47号命题是著名的毕达哥拉斯(勾股定理),证明过程中以直角三角形中的各边为边分别向外作了正方形(如图1).某校数学兴趣小组对上述图形结构作拓广探究,提出了如下问题,请帮忙解答.
问题:如图2,已知满足,,设(),四边形、四边形、四边形都是正方形.
(1)当时,求的长度;
(2)求长度的最大值.
【答案】(1)6 ; (2)6
【解析】(1)在中,,,,则,,
因为,所以
在中,,,
由余弦定理
所以的长度为.
(2)在中,由余弦定理得,所以,
设,在中,由余弦定理得,
所以 ①
在中,由正弦定理得,
所以,
代入①可得,
因为,
所以,
当即时,的最大值为,
所以长度的最大值为6.
同课章节目录
