14.2全等三角形的性质与判定综合练习(无答案)
文档属性
| 名称 | 14.2全等三角形的性质与判定综合练习(无答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 84.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-03-04 00:00:00 | ||
图片预览

文档简介
全等三角形的性质与判定综合应用(一)
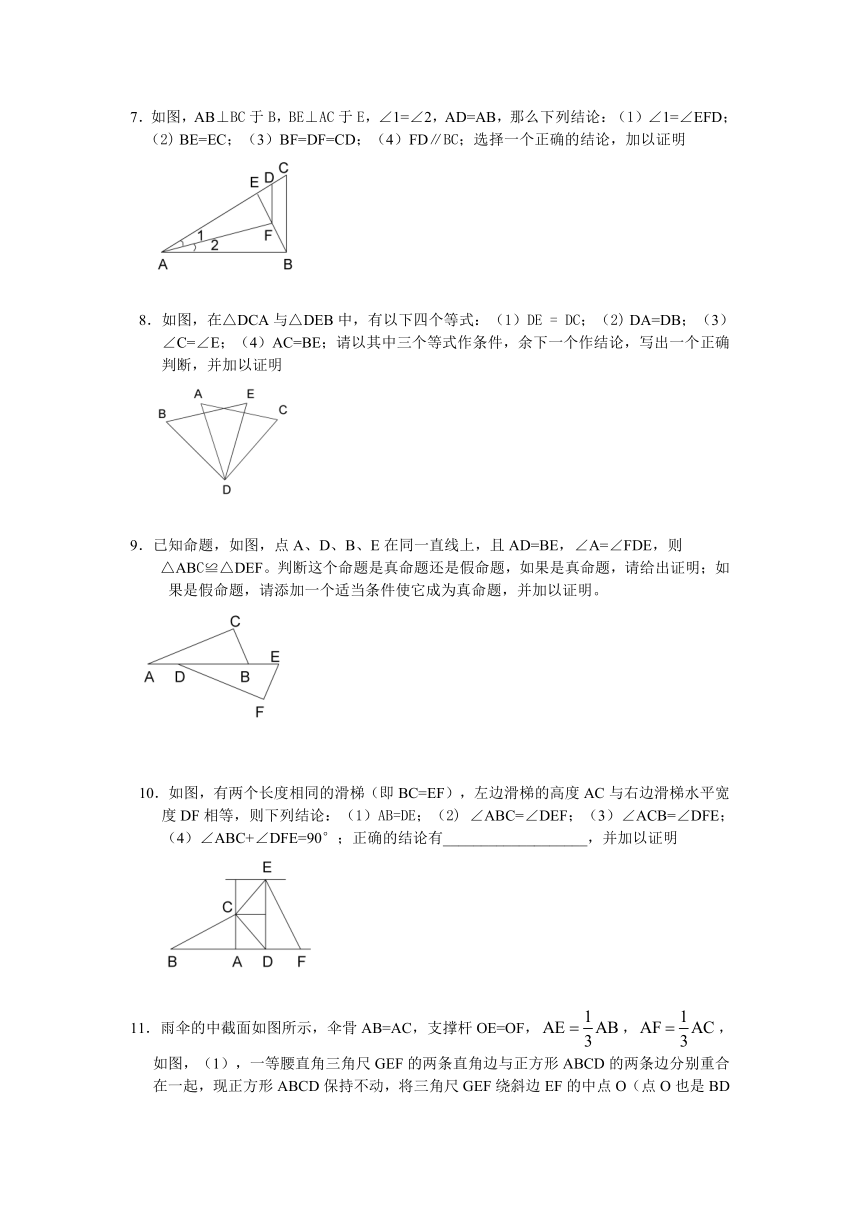
1.如图,在△ABC中,M在BC上,D 2.如图,已知AB=DC,AC=DB,
在AM上,AB=AC,DB=DC。 求证:∠1=∠2
求证:MB=MC
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
3.雨伞的中截面如图所示,伞骨AB=AC,支撑杆OE=OF,,,当O沿AD滑动时,雨伞开闭,问雨伞开闭过程中,∠BAD与∠CAD有何关系?说明理由
( http: / / www.21cnjy.com )
4.如图,AC⊥BC,BD⊥AD,AC、 ( http: / / www.21cnjy.com )BD交于点O,如果AC=BD,那么下列结论:(1)AD=BC;(2) ∠ABC=∠BAD;(3)∠DAC=∠CBD;(4)OC=OD;选择一个正确的结论,加以证明
( http: / / www.21cnjy.com )
5.如图所示,已知AB=AC,AD=AE, 6.如图,已知AB=AC,AE = AD,
∠BAC=∠DAE,BD=7cm,求CE 请写出一个与点D有关的正确结论,
的值 并加以证明
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
7.如图,AB⊥BC于B,BE⊥AC于E, ( http: / / www.21cnjy.com )∠1=∠2,AD=AB,那么下列结论:(1)∠1=∠EFD;(2) BE=EC;(3)BF=DF=CD;(4)FD∥BC;选择一个正确的结论,加以证明
( http: / / www.21cnjy.com )
8.如图,在△DCA与△DEB中,有以下四 ( http: / / www.21cnjy.com )个等式:(1)DE = DC;(2) DA=DB;(3)∠C=∠E;(4)AC=BE;请以其中三个等式作条件,余下一个作结论,写出一个正确判断,并加以证明
( http: / / www.21cnjy.com )
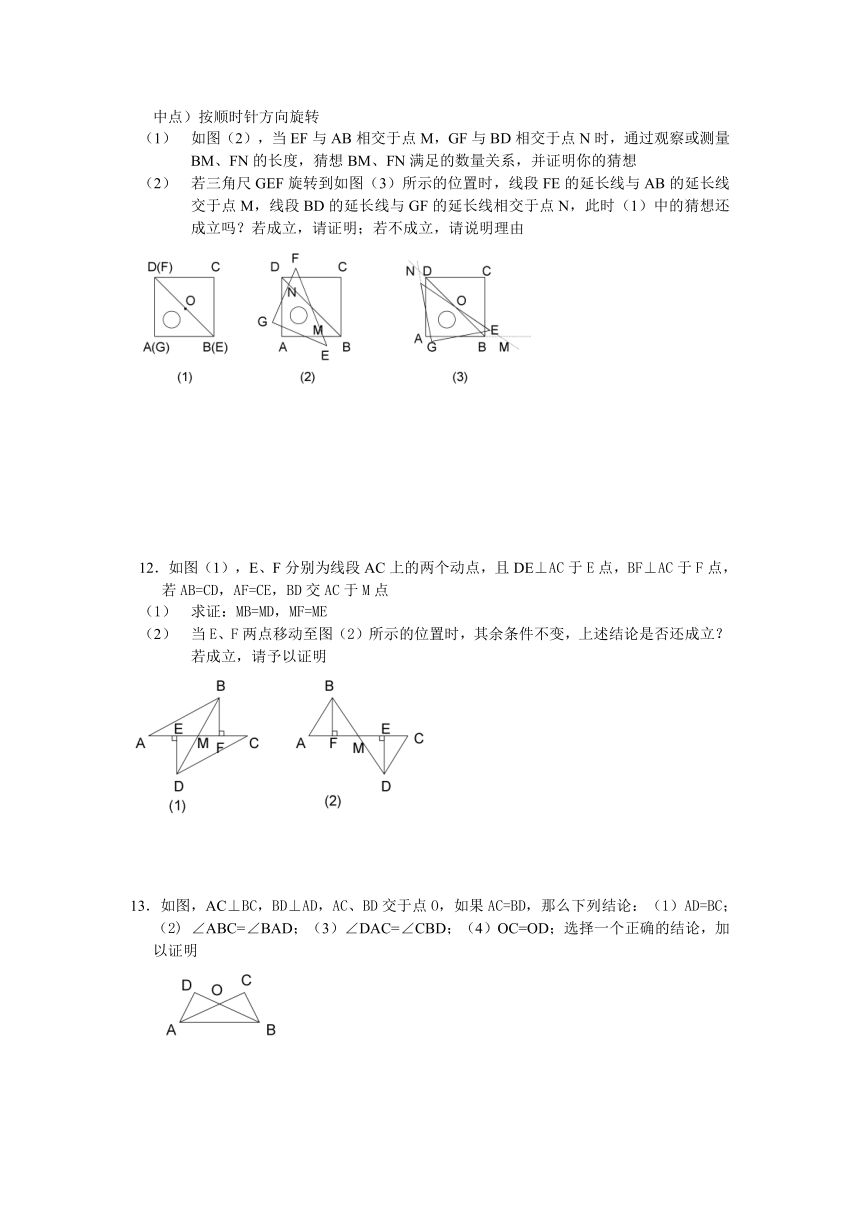
9.已知命题,如图,点A、D、B、E在同一直线上,且AD=BE,∠A=∠FDE,则
△ABC≌△DEF。判断这个命题是真命题还是假命题,如果是真命题,请给出证明;如果是假命题,请添加一个适当条件使它成为真命题,并加以证明。
( http: / / www.21cnjy.com )
10.如图,有两个长度相同 ( http: / / www.21cnjy.com )的滑梯(即BC=EF),左边滑梯的高度AC与右边滑梯水平宽度DF相等,则下列结论:(1)AB=DE;(2) ∠ABC=∠DEF;(3)∠ACB=∠DFE;(4)∠ABC+∠DFE=90°;正确的结论有___________________,并加以证明
( http: / / www.21cnjy.com )
11.雨伞的中截面如图所示,伞骨AB=AC,支撑杆OE=OF,,,如图,(1),一等腰直角三角尺GEF的两条直角边与正方形ABCD的两条边分别重合在一起,现正方形ABCD保持不动,将三角尺GEF绕斜边EF的中点O(点O也是BD中点)按顺时针方向旋转
如图(2),当EF与AB相交于点M,GF与BD相交于点N时,通过观察或测量BM、FN的长度,猜想BM、FN满足的数量关系,并证明你的猜想
若三角尺GEF旋转到如图(3)所示的位 ( http: / / www.21cnjy.com )置时,线段FE的延长线与AB的延长线交于点M,线段BD的延长线与GF的延长线相交于点N,此时(1)中的猜想还成立吗?若成立,请证明;若不成立,请说明理由
( http: / / www.21cnjy.com )
12.如图(1),E、F分别为线段AC上的两个动点,且DE⊥AC于E点,BF⊥AC于F点,若AB=CD,AF=CE,BD交AC于M点
求证:MB=MD,MF=ME
当E、F两点移动至图(2)所示的位置时,其余条件不变,上述结论是否还成立?若成立,请予以证明
( http: / / www.21cnjy.com )
13.如图,AC⊥BC,BD⊥AD ( http: / / www.21cnjy.com ),AC、BD交于点O,如果AC=BD,那么下列结论:(1)AD=BC;(2) ∠ABC=∠BAD;(3)∠DAC=∠CBD;(4)OC=OD;选择一个正确的结论,加以证明
( http: / / www.21cnjy.com )
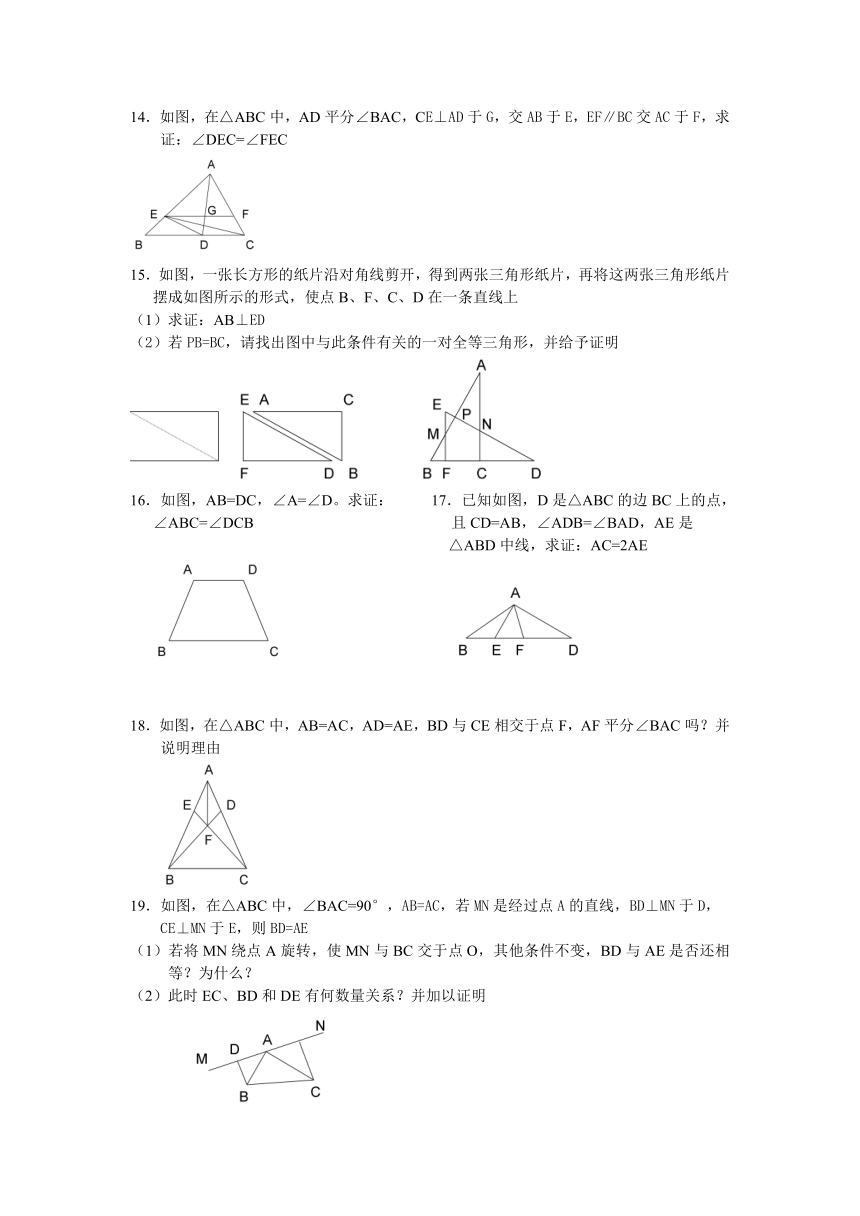
14.如图,在△ABC中,AD平分∠BAC,CE⊥AD于G,交AB于E,EF∥BC交AC于F,求证:∠DEC=∠FEC
( http: / / www.21cnjy.com )
15.如图,一张长方形的纸片沿对角线剪开,得到两张三角形纸片,再将这两张三角形纸片摆成如图所示的形式,使点B、F、C、D在一条直线上
(1)求证:AB⊥ED
(2)若PB=BC,请找出图中与此条件有关的一对全等三角形,并给予证明
( http: / / www.21cnjy.com )
16.如图,AB=DC,∠A=∠D。求证: 17.已知如图,D是△ABC的边BC上的点,
∠ABC=∠DCB 且CD=AB,∠ADB=∠BAD,AE是
△ABD中线,求证:AC=2AE
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
18.如图,在△ABC中,AB=AC,AD=AE,BD与CE相交于点F,AF平分∠BAC吗?并说明理由
( http: / / www.21cnjy.com )
19.如图,在△ABC中,∠BAC=90°,AB=AC,若MN是经过点A的直线,BD⊥MN于D,
CE⊥MN于E,则BD=AE
(1)若将MN绕点A旋转,使MN与BC交于点O,其他条件不变,BD与AE是否还相等?为什么?
(2)此时EC、BD和DE有何数量关系?并加以证明
( http: / / www.21cnjy.com )
全等三角形的性质与判定综合应用(二)
如图,AB=AC,AD=AE,∠BAC=∠DAE,△ABD与△ACE全等吗?请说明理由
( http: / / www.21cnjy.com )
如图△ABC≌△DEF,AM、DN分别是△ABC和△DEF的角平分线,AM与DN相对吗?请说明理由
( http: / / www.21cnjy.com )
如图,点E、F在BC上,BE=CF,AB=DC,∠B=∠C,求证:∠A=∠D
( http: / / www.21cnjy.com )
如图,∠1=∠2,请你添加一个条件,求证:AB=AC
( http: / / www.21cnjy.com )
5.如图,在△ABC和△ADE中,∠BAC=∠DAE,AB=AE,AC=AD,连接BD、CE。求证:△ABD≌△AEC
( http: / / www.21cnjy.com )
7.如图,AB=CD,AE=DF,CE=FB。求证:AF=DE
( http: / / www.21cnjy.com )
8.如图,D是△ABC中BC边的中点,EB=EC,∠ABE=∠ACE,求证:∠BAE=∠CAE
( http: / / www.21cnjy.com )
9.如图,AB=AC,BD=CD,DE⊥AB于点E,DF⊥AC于点F,求证:DE=DF
( http: / / www.21cnjy.com )
10.如图,在△ABC中,AB=C ( http: / / www.21cnjy.com )B,∠ABC=90°,D为AB延长线上一点,点E在BC边上,且BE=BD,连接AE、DE、DC。(1)求证:△ABE≌△CBD;(2)若∠CAE=30°,求
∠BDC
( http: / / www.21cnjy.com )
11.如图,AB=AE,BC=ED,∠B=∠E,AF⊥CD,F为垂足,求证:CF=DF
( http: / / www.21cnjy.com )
12.如图,点D为锐角∠ABC内一点,点M在边BA上,点N在边BC上,且DM=DN,∠BMD+∠BND=180°.求证:BD平分∠ABC
( http: / / www.21cnjy.com )
13.如图,在△ABC中,∠ABC=2∠C,∠BAC的平分线交BC于点D。求证:AB+BD=AC
( http: / / www.21cnjy.com )
16.如图,在梯形ABCD中,AD∥BC,B ( http: / / www.21cnjy.com )C=DC,CF平分∠BCD,DF∥AB,BF的延长线交DC于点E。求证:(1)△BFC≌△DFC;(2)AD=DE
( http: / / www.21cnjy.com )
17.如图,在△ABC中, ( http: / / www.21cnjy.com )AB=CB,∠ABC=90°,D为AB延长线上一点,点E在BC边上,且BE=BD,连接AE、DE、DC。(1)求证:△ABE≌△CBD;(2)若∠CAE=30°,求
∠BDC
( http: / / www.21cnjy.com )
18.在△ABC和△A1 ( http: / / www.21cnjy.com )B1C1中,AD是BC边上的高,A1D1是B1C1边上的高,若AD= A1D1,AB= A1B1,AC= A1C1,试猜想∠C与∠A1 C1B1的关系,并加以说明。
1.如图,在△ABC中,M在BC上,D 2.如图,已知AB=DC,AC=DB,
在AM上,AB=AC,DB=DC。 求证:∠1=∠2
求证:MB=MC
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
3.雨伞的中截面如图所示,伞骨AB=AC,支撑杆OE=OF,,,当O沿AD滑动时,雨伞开闭,问雨伞开闭过程中,∠BAD与∠CAD有何关系?说明理由
( http: / / www.21cnjy.com )
4.如图,AC⊥BC,BD⊥AD,AC、 ( http: / / www.21cnjy.com )BD交于点O,如果AC=BD,那么下列结论:(1)AD=BC;(2) ∠ABC=∠BAD;(3)∠DAC=∠CBD;(4)OC=OD;选择一个正确的结论,加以证明
( http: / / www.21cnjy.com )
5.如图所示,已知AB=AC,AD=AE, 6.如图,已知AB=AC,AE = AD,
∠BAC=∠DAE,BD=7cm,求CE 请写出一个与点D有关的正确结论,
的值 并加以证明
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
7.如图,AB⊥BC于B,BE⊥AC于E, ( http: / / www.21cnjy.com )∠1=∠2,AD=AB,那么下列结论:(1)∠1=∠EFD;(2) BE=EC;(3)BF=DF=CD;(4)FD∥BC;选择一个正确的结论,加以证明
( http: / / www.21cnjy.com )
8.如图,在△DCA与△DEB中,有以下四 ( http: / / www.21cnjy.com )个等式:(1)DE = DC;(2) DA=DB;(3)∠C=∠E;(4)AC=BE;请以其中三个等式作条件,余下一个作结论,写出一个正确判断,并加以证明
( http: / / www.21cnjy.com )
9.已知命题,如图,点A、D、B、E在同一直线上,且AD=BE,∠A=∠FDE,则
△ABC≌△DEF。判断这个命题是真命题还是假命题,如果是真命题,请给出证明;如果是假命题,请添加一个适当条件使它成为真命题,并加以证明。
( http: / / www.21cnjy.com )
10.如图,有两个长度相同 ( http: / / www.21cnjy.com )的滑梯(即BC=EF),左边滑梯的高度AC与右边滑梯水平宽度DF相等,则下列结论:(1)AB=DE;(2) ∠ABC=∠DEF;(3)∠ACB=∠DFE;(4)∠ABC+∠DFE=90°;正确的结论有___________________,并加以证明
( http: / / www.21cnjy.com )
11.雨伞的中截面如图所示,伞骨AB=AC,支撑杆OE=OF,,,如图,(1),一等腰直角三角尺GEF的两条直角边与正方形ABCD的两条边分别重合在一起,现正方形ABCD保持不动,将三角尺GEF绕斜边EF的中点O(点O也是BD中点)按顺时针方向旋转
如图(2),当EF与AB相交于点M,GF与BD相交于点N时,通过观察或测量BM、FN的长度,猜想BM、FN满足的数量关系,并证明你的猜想
若三角尺GEF旋转到如图(3)所示的位 ( http: / / www.21cnjy.com )置时,线段FE的延长线与AB的延长线交于点M,线段BD的延长线与GF的延长线相交于点N,此时(1)中的猜想还成立吗?若成立,请证明;若不成立,请说明理由
( http: / / www.21cnjy.com )
12.如图(1),E、F分别为线段AC上的两个动点,且DE⊥AC于E点,BF⊥AC于F点,若AB=CD,AF=CE,BD交AC于M点
求证:MB=MD,MF=ME
当E、F两点移动至图(2)所示的位置时,其余条件不变,上述结论是否还成立?若成立,请予以证明
( http: / / www.21cnjy.com )
13.如图,AC⊥BC,BD⊥AD ( http: / / www.21cnjy.com ),AC、BD交于点O,如果AC=BD,那么下列结论:(1)AD=BC;(2) ∠ABC=∠BAD;(3)∠DAC=∠CBD;(4)OC=OD;选择一个正确的结论,加以证明
( http: / / www.21cnjy.com )
14.如图,在△ABC中,AD平分∠BAC,CE⊥AD于G,交AB于E,EF∥BC交AC于F,求证:∠DEC=∠FEC
( http: / / www.21cnjy.com )
15.如图,一张长方形的纸片沿对角线剪开,得到两张三角形纸片,再将这两张三角形纸片摆成如图所示的形式,使点B、F、C、D在一条直线上
(1)求证:AB⊥ED
(2)若PB=BC,请找出图中与此条件有关的一对全等三角形,并给予证明
( http: / / www.21cnjy.com )
16.如图,AB=DC,∠A=∠D。求证: 17.已知如图,D是△ABC的边BC上的点,
∠ABC=∠DCB 且CD=AB,∠ADB=∠BAD,AE是
△ABD中线,求证:AC=2AE
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
18.如图,在△ABC中,AB=AC,AD=AE,BD与CE相交于点F,AF平分∠BAC吗?并说明理由
( http: / / www.21cnjy.com )
19.如图,在△ABC中,∠BAC=90°,AB=AC,若MN是经过点A的直线,BD⊥MN于D,
CE⊥MN于E,则BD=AE
(1)若将MN绕点A旋转,使MN与BC交于点O,其他条件不变,BD与AE是否还相等?为什么?
(2)此时EC、BD和DE有何数量关系?并加以证明
( http: / / www.21cnjy.com )
全等三角形的性质与判定综合应用(二)
如图,AB=AC,AD=AE,∠BAC=∠DAE,△ABD与△ACE全等吗?请说明理由
( http: / / www.21cnjy.com )
如图△ABC≌△DEF,AM、DN分别是△ABC和△DEF的角平分线,AM与DN相对吗?请说明理由
( http: / / www.21cnjy.com )
如图,点E、F在BC上,BE=CF,AB=DC,∠B=∠C,求证:∠A=∠D
( http: / / www.21cnjy.com )
如图,∠1=∠2,请你添加一个条件,求证:AB=AC
( http: / / www.21cnjy.com )
5.如图,在△ABC和△ADE中,∠BAC=∠DAE,AB=AE,AC=AD,连接BD、CE。求证:△ABD≌△AEC
( http: / / www.21cnjy.com )
7.如图,AB=CD,AE=DF,CE=FB。求证:AF=DE
( http: / / www.21cnjy.com )
8.如图,D是△ABC中BC边的中点,EB=EC,∠ABE=∠ACE,求证:∠BAE=∠CAE
( http: / / www.21cnjy.com )
9.如图,AB=AC,BD=CD,DE⊥AB于点E,DF⊥AC于点F,求证:DE=DF
( http: / / www.21cnjy.com )
10.如图,在△ABC中,AB=C ( http: / / www.21cnjy.com )B,∠ABC=90°,D为AB延长线上一点,点E在BC边上,且BE=BD,连接AE、DE、DC。(1)求证:△ABE≌△CBD;(2)若∠CAE=30°,求
∠BDC
( http: / / www.21cnjy.com )
11.如图,AB=AE,BC=ED,∠B=∠E,AF⊥CD,F为垂足,求证:CF=DF
( http: / / www.21cnjy.com )
12.如图,点D为锐角∠ABC内一点,点M在边BA上,点N在边BC上,且DM=DN,∠BMD+∠BND=180°.求证:BD平分∠ABC
( http: / / www.21cnjy.com )
13.如图,在△ABC中,∠ABC=2∠C,∠BAC的平分线交BC于点D。求证:AB+BD=AC
( http: / / www.21cnjy.com )
16.如图,在梯形ABCD中,AD∥BC,B ( http: / / www.21cnjy.com )C=DC,CF平分∠BCD,DF∥AB,BF的延长线交DC于点E。求证:(1)△BFC≌△DFC;(2)AD=DE
( http: / / www.21cnjy.com )
17.如图,在△ABC中, ( http: / / www.21cnjy.com )AB=CB,∠ABC=90°,D为AB延长线上一点,点E在BC边上,且BE=BD,连接AE、DE、DC。(1)求证:△ABE≌△CBD;(2)若∠CAE=30°,求
∠BDC
( http: / / www.21cnjy.com )
18.在△ABC和△A1 ( http: / / www.21cnjy.com )B1C1中,AD是BC边上的高,A1D1是B1C1边上的高,若AD= A1D1,AB= A1B1,AC= A1C1,试猜想∠C与∠A1 C1B1的关系,并加以说明。
