专题6.4 平行四边形的判定(分层练习)(基础练)(含解析)
文档属性
| 名称 | 专题6.4 平行四边形的判定(分层练习)(基础练)(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-26 22:23:40 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
专题6.4 平行四边形的判定(分层练习)(基础练)
一、单选题(本大题共10小题,每小题3分,共30分)
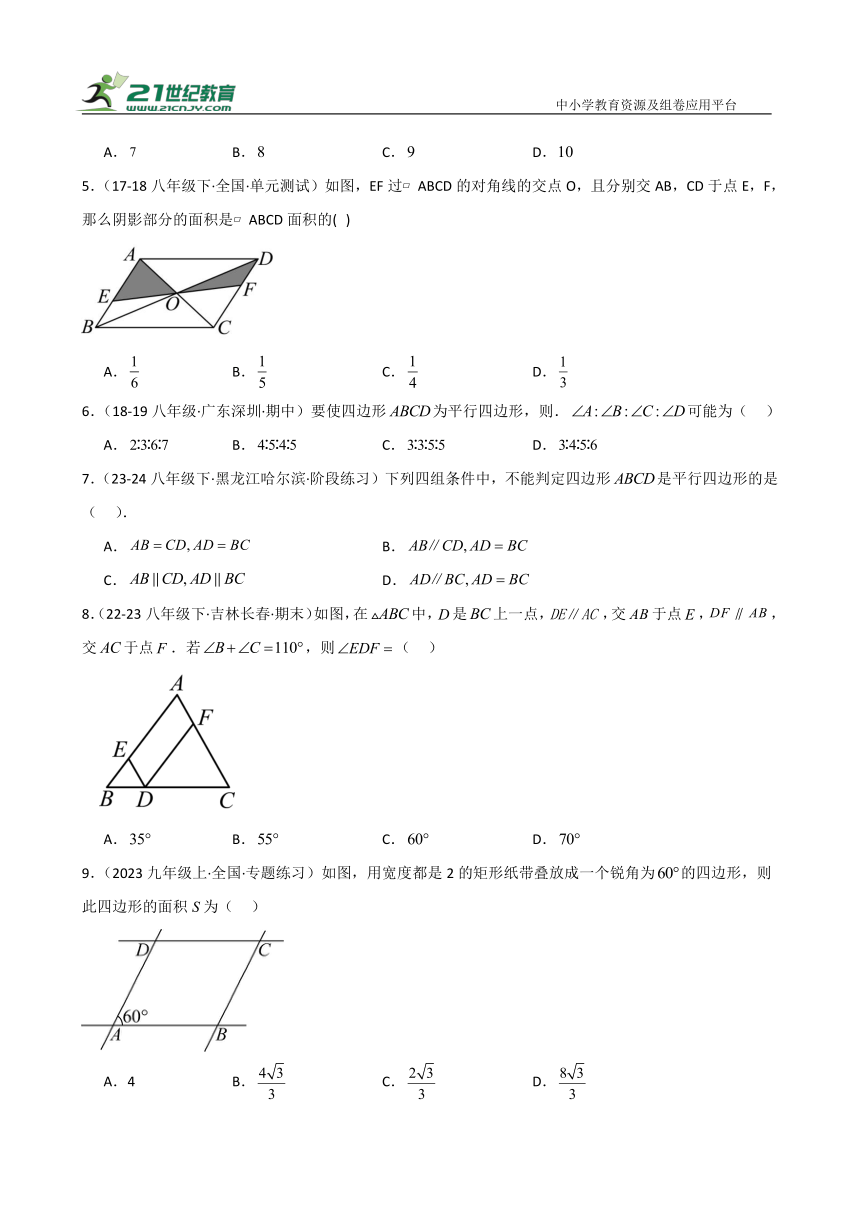
1.(23-24八年级下·吉林松原·期中)如图,已知,增加下列条件可以使四边形成为平行四边形的是( )
A. B. C. D.
2.(23-24八年级下·福建福州·期中)如图,,,,,的面积为,则四边形的面积为( )
A.6 B.10 C.20 D.40
3.(2023·四川成都·模拟预测)如图,在中,,分别以点A,C为圆心,长为半径画弧,两弧在直线上方交于点D,连接,则的度数是( )
A. B. C. D.
4.(2023·浙江舟山·模拟预测)如图,在中,点分别在的延长线上,且满足.若,,则的长为( )
A. B. C. D.
5.(17-18八年级下·全国·单元测试)如图,EF过 ABCD的对角线的交点O,且分别交AB,CD于点E,F,那么阴影部分的面积是 ABCD面积的( )
A. B. C. D.
6.(18-19八年级·广东深圳·期中)要使四边形为平行四边形,则.可能为( )
A. B. C. D.
7.(23-24八年级下·黑龙江哈尔滨·阶段练习)下列四组条件中,不能判定四边形是平行四边形的是( ).
A. B.
C. D.
8.(22-23八年级下·吉林长春·期末)如图,在中,是上一点,,交于点,,交于点.若,则( )
A. B. C. D.
9.(2023九年级上·全国·专题练习)如图,用宽度都是2的矩形纸带叠放成一个锐角为的四边形,则此四边形的面积S为( )
A.4 B. C. D.
10.(2023·湖北黄石·模拟预测)如图所示平面直角坐标系, 中,. 将绕着的中点M旋转,则点O的对应点的坐标为( )
A. B. C. D.
二、填空题(本大题共8小题,每小题4分,共32分)
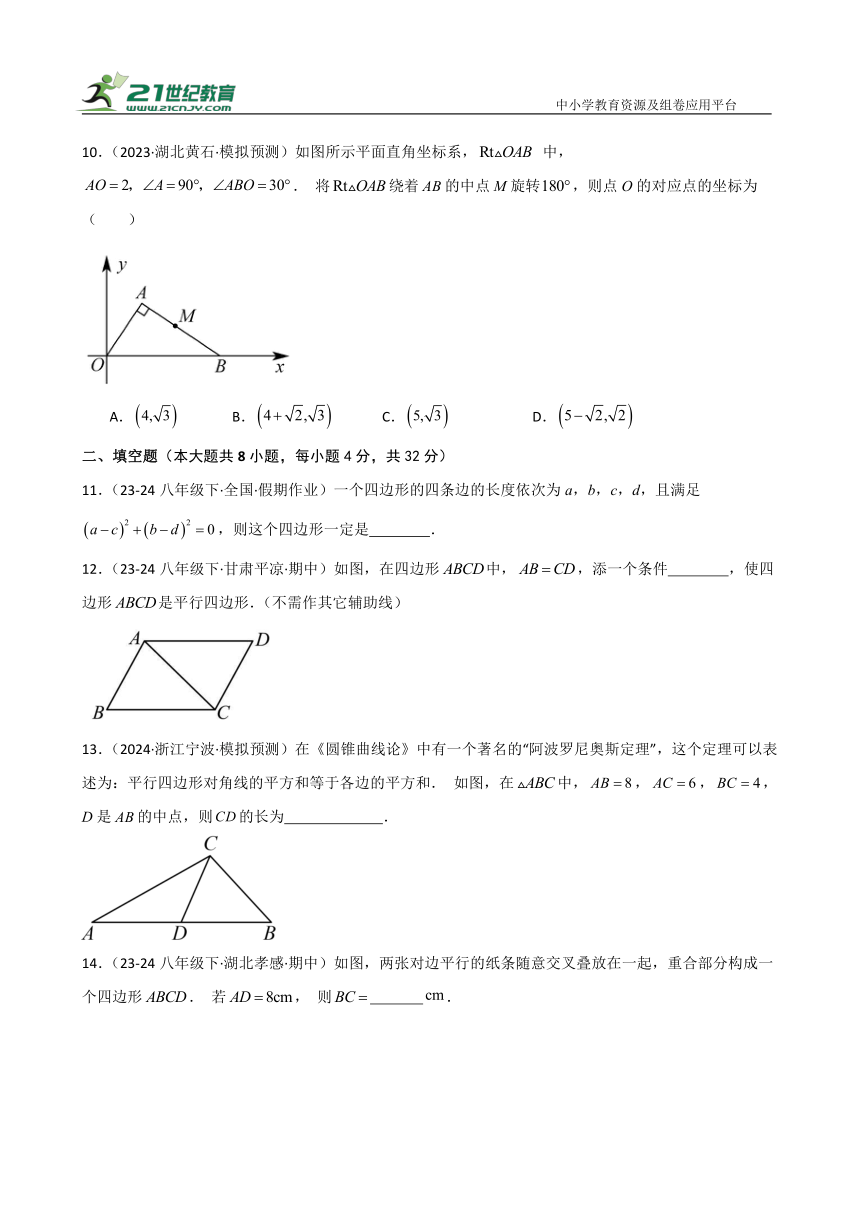
11.(23-24八年级下·全国·假期作业)一个四边形的四条边的长度依次为a,b,c,d,且满足,则这个四边形一定是 .
12.(23-24八年级下·甘肃平凉·期中)如图,在四边形中,,添一个条件 ,使四边形是平行四边形.(不需作其它辅助线)
13.(2024·浙江宁波·模拟预测)在《圆锥曲线论》中有一个著名的“阿波罗尼奥斯定理”,这个定理可以表述为:平行四边形对角线的平方和等于各边的平方和. 如图,在中,,,,D是的中点,则的长为 .
14.(23-24八年级下·湖北孝感·期中)如图,两张对边平行的纸条随意交叉叠放在一起,重合部分构成一个四边形. 若, 则 .
15.(23-24八年级下·湖北黄冈·期中)在四边形中,,,,则 .
16.(2012·贵州黔西·中考真题)如图,在△ABC中,∠ACB=90°,D是BC的中点,DE⊥BC,CE//AD,若AC=2,CE=4,则四边形ACEB的周长为 .
17.(2024·辽宁·模拟预测)如图,在中,,连接,过点A作交的延长线于点E,过点E作交的延长线于点F,若,则 .
18.(21-22八年级下·北京朝阳·期末)已知直线及线段,点在直线上,点在直线外.如图.
(1)在直线上取一点(不与点重合),连接;
(2)以点为圆心,长为半径作弧,以点为圆心,长为半径作弧,两弧交于点(与点位于直线异侧);
(3)连接交于点,连接,.
根据以上作图过程及所作图形,在下列结论①;②;③中,一定正确的是 (填写所有正确的序号).
三、解答题(本大题共6小题,共58分)
19.(8分)19.(23-24九年级下·浙江杭州·期中)如图,已知,,.
(1)求证:;
(2)连接,那么相等吗?请说明理由.
20.(8分)(2024·湖南岳阳·一模)如图,点、、、在一条直线上,且,.
(1)求证:;
(2)求证:四边形是平行四边形.
21.(10分)(2024八年级下·北京·专题练习)如图,在平行四边形中,F是的中点,延长到点E.使,连接、.
(1)求证:;
(2)若,,.求的长.
22.(10分)(23-24八年级下·山东济南·期中)如图,中,E、F为对角线上的两点,且,连接,.
(1)求证:.
(2)连接、,求证:四边形是平行四边形.
23.(10分)(23-24八年级下·河南商丘·期中)如图,以的三边为边,在的同一侧分别作等边三角形,等边三角形,等边三角形,连接.
(1)判断四边形的形状,并证明你的结论.
(2)若,求的度数.
24.(12分)(22-23八年级下·北京海淀·期末)(1)探究规律:
已知:如图,点为平行四边形内一点, 、 的面积分别记为 、 ,平行四边形的面积记为,试探究与之间的关系.
(2)解决问题:
如图矩形中,,,点、、、分别在、、、上,且,.点为矩形内一点,四边形、四边形 的面积分别记为、,求.
中小学教育资源及组卷应用平台
试卷第1页,共3页
参考答案:
1.C
【分析】此题考查了平行四边形的判定,全等三角形的判定与性质,根据平行四边形的判定定理逐项判断即可,解题的关键是熟知平行四边形的判定定理.
【详解】、由可得,结合题意,不能证明四边形成为平行四边形,不符合题意;
、由,结合题意,不能证明四边形成为平行四边形,不符合题意;
、∵,
∴,
又,,
∴,
∴,
∴四边形是平行四边形,符合题意;
、由,结合题意,不能证明四边形成为平行四边形,不符合题意;
故选:.
2.C
【分析】本题考查了平行四边形的判定和性质以及三角形的面积.先判断四边形为平行四边形得到,则,再利用得到点和点到的距离相等,设点到的距离为,利用的面积为可计算出,然后根据平行四边形的面积公式计算四边形的面积.
【详解】解:,
四边形为平行四边形,
,
,
,
点和点到直线的距离相等,
设点到的距离为,
的面积为,
,
解得,
四边形的面积.
故选:C.
3.D
【分析】本题考查了平行四边形的判定与性质,熟练掌握平行四边形的判定与性质是解题关键.先判断出四边形是平行四边形,再根据平行四边形的性质求解即可得.
【详解】解:由题意得:,
∴四边形是平行四边形,
∴,
故选:D.
4.B
【分析】根据平行四边形的性质,,可得是等腰三角形,再根据,可得四边形是平行四边形,根据,由此即可求解.
【详解】解:∵四边形是平四边形,
∴,,
∵,
∴,
∵,
∴,
∴是等腰三角形,即,
∵,,点在的延长线上,
∴,
∴四边形是平行四边形,
∴,
∴,
∴,
故选:.
【点拨】本题主要考查平行四边形的判定和性质,等腰三角形的判定和性质的综合,掌握以上知识的综合运用是解题的关键.
5.C
【分析】利用平行四边形对角线互相平分,中线将三角形面积平分这一性质解题.
【详解】∵四边形ABCD是平行四边形,EF经过对角线交点O,
∴易得S△BEO=S△DFO,
∴S阴影部分=S△AOB=S ABCD
故选C.
【点拨】本题考查了平行四边形的面积,属于简单题,熟悉平行四边形性质和中线性质是解题关键.
6.B
【分析】本题考查了平行四边形的判定,在应用判定定理判定平行四边形时,应仔细观察题目所给的条件,仔细选择适合于题目的判定方法进行解答,避免混用判定方法.根据平行四边形的判定:两组对角分别相等的四边形是平行四边形,据此判断即可.
【详解】解:根据平行四边形的判定:两组对角分别相等的四边形是平行四边形,和是对角,和是对角,对角的份数应相等.只有选项B符合.
故选:B
7.B
【分析】此题主要考查了平行四边形的判定,解题的关键是掌握平行四边形的判定定理.根据平行四边形的判定定理分别进行分析即可.
【详解】解:A、,根据两组对边分别相等的四边形是平行四边形可判定四边形为平行四边形,故此选项不合题意;
B、,不能判定四边形是平行四边形,可能是等腰梯形,故此选项符合题意;
C、,根据两组对边分别平行的四边形是平行四边形可判定四边形为平行四边形,故此选项不合题意;
D、,根据一组对边平行且相等的四边形是平行四边形可判定四边形为平行四边形,故此选项不合题;
故选:B
8.D
【分析】根据已知判定四边形是平行四边形,得到,再根据三角形内角和定理求解.
【详解】解:∵,,
∴四边形是平行四边形,
∴,
∵,
∴,
故选:D.
【点拨】本题考查了平行四边形的判定和性质,三角形内角和,解题的关键是根据平行四边形得到.
9.D
【分析】先根据两组对边分别平行证明四边形是平行四边形,再根据两张纸条的宽度相等,利用面积求出,然后根据邻边相等的平行四边形是菱形即可证明;根据宽度是2与求出菱形的边长,然后利用菱形的面积底高计算即可.
【详解】解:纸条的对边平行,即,,
∴四边形是平行四边形,
过A作,垂足为E,
∵两张纸条的宽度都是2,
∴,
∵,
∴,
∴,
在中,,
即,
∴,负值舍去,
∴.
故选:D.
【点拨】本题考查了平行四边形的判定与性质,勾股定理,直角三角形的性质,解题的关键是根据勾股定理求出.
10.C
【分析】连接并延长交y轴于E,连接,求出的长度即可求解.
【详解】解:连接并延长交y轴于E,连接,
∵,
∴四边形是平行四边形,
∴x轴,,
∴y轴,
∵,
∴,
∴,
∴
∵,
∴,
∴点O的对应点的坐标为,
故选:C.
【点拨】本题考查了旋转的性质、含的直角三角形.掌握相关结论是解题关键.
11.平行四边形
【解析】略
12.(或或者)答案不唯一
【分析】本题考查了平行四边形的判定,是开放题,答案不唯一,利用平行四边形的判定方法来添加条件,平行四边形的判定方法共有五种,在四边形中如果有:1、四边形的两组对边分别平行,2、一组对边平行且相等,3、两组对边分别相等,4、对角线互相平分,5、两组对角分别相等.则四边形是平行四边形.
根据平行四边形的判定方法,可以再加一个:的条件,利用两组对边分别相等的四边形是平行四边形而得证.
【详解】解:根据平行四边形的判定,可添加:(答案不唯一).
故答案为:(或或).
13.
【分析】本题考查了平行四边形的判定和性质,熟练运用阿波罗尼奥斯定理是解题的关键.
延长到E,使,连接,,根据线段中点的定义得到,推出四边形是平行四边形,得到,,根据阿波罗尼奥斯定理解方程即可得出结论.
【详解】解:延长到E,使,连接,,
点D是的中点,
,
,
四边形是平行四边形,
,,
由阿波罗尼奥斯定理得:,
,
,
,
故答案为:.
14.8
【分析】本题主要考查平行四边形的判定和性质,掌握平行四边形的判定和性质是解题的关键.由条件可知,可证明四边形为平行四边形,可得到.
【详解】解:∵,
∴四边形为平行四边形,
∴.
故答案为:8
15./50度
【分析】本题考查平行四边形的判定和性质,解题的关键是熟练掌握基本知识,属于中考基础题.
证明四边形是平行四边形,再利用其性质即可解决问题
【详解】
解:,,
四边形是平行四边形,
,
,
,
故答案为:.
16./
【分析】先证明四边形ACED是平行四边形,可得DE=AC=2.由勾股定理和中线的定义可求AB和EB的长,从而求出四边形ACEB的周长.
【详解】∵∠ACB=90°,DE⊥BC,
∴AC∥DE.
又∵CE∥AD,
∴四边形ACED是平行四边形.
∴DE=AC=2.
在Rt△CDE中,DE= 2,CE=4,由勾股定理得.
∵D是BC的中点,
∴BC=2CD=4.
在△ABC中,∠ACB=90°,由勾股定理得.
∵D是BC的中点,DE⊥BC,
∴EB=EC=4.
∴四边形ACEB的周长=AC+CE+EB+BA=10+.
故答案为:10+.
17.
【分析】本题考查了平行四边形的判定与性质、含30度角的直角三角形的性质,熟练掌握平行四边形的判定与性质是解题关键.
先根据平行四边形的判定与性质可得四边形是平行四边形,根据平行四边形的性质可得,从而可得,再根据含30度角的直角三角形的性质可得,由此即可得.
【详解】解:∵四边形是平行四边形,,
∴,,
∵,
∴四边形是平行四边形,
∴,
∴,
∵,
∴,
∵,
∴,
∴,
∴,
故答案为:2.
18.①②/②①
【分析】
根据作图可得,则四边形是平行四边形,进而即可求解.
【详解】解:根据作图可得,则四边形是平行四边形,
∴,;故①②正确,
∵不一定相等,则不一定成立,即③不一定正确;
故答案为:①②.
【点拨】本题考查了平行四边形的性质与判定,熟练掌握基本作图以及平行四边形的性质与判定是解题的关键.
19.(1)见解析
(2)相等,见解析
【分析】本题考查全等三角形的判定与性质,平行线的判定与性质,平行四边形的判定与性质.
(1)由得,即,由得,进而可得,再用边角边证明其全等即可;
(2)由得,,故,得出四边形是平行四边形即可.
【详解】(1)证明:∵,
∴,即
∵,
∴,
∵,
∴
在和中
∴;
(2)解:相等.理由如下:
∵
∴,,
∴
∴四边形是平行四边形
∴.
20.(1)见解析
(2)见解析
【分析】本题考查了平行线的判定与性质,全等三角形的判定与性质,平行四边形的判定,解题关键是掌握全等三角形的判定与性质及平行四边形的判定方法.
(1)根据平行线的性质“两直线平行,内错角相等”得,再根据,等量交换得,结合已知条件,根据全等三角形判定(边角边),得,即可得;
(2)根据(1)得,由全等三角形的性质得,,根据平行线的判定“内错角相等,两直线平行”得,再根据平行四边形的判定“一组对边平行且相等的四边形是平行四边形”,即可证得结论.
【详解】(1)证明:,
,
又,
,
即,
在和中,
,
,
.
(2)证明:由(1)得,
,,
,
四边形是平行四边形.
21.(1)见解析
(2)
【分析】本题主要考查了平行四边形的判定以及性质,平行线的性质以及勾股定理解三角形等知识点.
(1)由平行四边形的性质得出,且,由中点的定义得出,结合已知条件即可得出,进一步证明四边形是平行四边形,再由平行四边形的性质可得出.
(2)过点C作于点H.由平行线的性质得出,则,由勾股定理求出,由平行四边形的性质得出,即可求出,再利用勾股定理即可求出.
【详解】(1)证明:∵四边形是平行四边形,
∴,且,
∵F是的中点,
∴,
又∵,
∴,
∵,
∴四边形是平行四边形,
∴;
(2)如图,过点C作于点H.
在中,,,
∴.
∵,,
∴,,
在中,,
∴,
∴,
由(1)可知,四边形是平行四边形,
∴,
∴,
在,根据勾股定理得:
.
22.(1)见解析
(2)见解析
【分析】本题主要考查了全等三角形的判定和性质,平行四边形的判定和性质,平行线的判定和性质,解题的关键是熟练掌握相关的判定和性质.
(1)根据四边形的性质得出,,证明,得出即可;
(2)根据,得出,,证明,即可证明结论.
【详解】(1)证明:∵四边形为平行四边形,
∴,,
∴,
在与中
,
∴,
∴.
(2)证明:连接、.
由(1)得,,
∴,,
∵,,
∴,
∴,
∴四边形为平行四边形.
23.(1)四边形是平行四边形,证明见详解
(2)
【分析】(1)根据等边三角形的性质推出,求出,证,推出,同理得出,即可得出结论.
(2)先根据等边三角形的性质,得出,结合周角概念列式,得出,根据平行四边形的性质,即可作答.
此题主要考查了等边三角形的性质和平行四边形的判定.
【详解】(1)证明:四边形是平行四边形,证明如下:
、、都是等边三角形,
,,,,
,
即,
在和中,
,
,
,
,
,
同理,
四边形是平行四边形.
(2)解:∵都是等边三角形,
∴
∵
∴
∵四边形是平行四边形.
∴.
24.(1),证明见解析;(2)
【分析】(1)如图所示,过点作,作延长线于点,延长交于点,可得平行四边形与同底同高,平行四边形与同底同高,由此即可求解;
(2)如图所示,连接、、、得四边形,可证,,即四边形是平行四边形,并可求出,,由此可求出平行四边形的面积,由(1)的计算方法即可求解.
【详解】证明:(1),理由如下,
如图所示,过点作,作延长线于点,延长交于点,
∵四边形是平行四边形,
∴,
∴,,,
∴,,,
∴,.
∵,
,
.
解:(2)如图所示,连接、、、得四边形,
∵四边形是矩形,
∴,,,
∵,,,
∴,
∴,且,
同理可得,,,,,,
∴四边形为平行四边形,,
∴,
由(1)可得,
∴.
【点拨】本题主要考查平行四边形的性质、矩形的性质及不规则图形面积的计算方法,掌握已知知识的综合运用是解题的关键.
专题6.4 平行四边形的判定(分层练习)(基础练)
一、单选题(本大题共10小题,每小题3分,共30分)
1.(23-24八年级下·吉林松原·期中)如图,已知,增加下列条件可以使四边形成为平行四边形的是( )
A. B. C. D.
2.(23-24八年级下·福建福州·期中)如图,,,,,的面积为,则四边形的面积为( )
A.6 B.10 C.20 D.40
3.(2023·四川成都·模拟预测)如图,在中,,分别以点A,C为圆心,长为半径画弧,两弧在直线上方交于点D,连接,则的度数是( )
A. B. C. D.
4.(2023·浙江舟山·模拟预测)如图,在中,点分别在的延长线上,且满足.若,,则的长为( )
A. B. C. D.
5.(17-18八年级下·全国·单元测试)如图,EF过 ABCD的对角线的交点O,且分别交AB,CD于点E,F,那么阴影部分的面积是 ABCD面积的( )
A. B. C. D.
6.(18-19八年级·广东深圳·期中)要使四边形为平行四边形,则.可能为( )
A. B. C. D.
7.(23-24八年级下·黑龙江哈尔滨·阶段练习)下列四组条件中,不能判定四边形是平行四边形的是( ).
A. B.
C. D.
8.(22-23八年级下·吉林长春·期末)如图,在中,是上一点,,交于点,,交于点.若,则( )
A. B. C. D.
9.(2023九年级上·全国·专题练习)如图,用宽度都是2的矩形纸带叠放成一个锐角为的四边形,则此四边形的面积S为( )
A.4 B. C. D.
10.(2023·湖北黄石·模拟预测)如图所示平面直角坐标系, 中,. 将绕着的中点M旋转,则点O的对应点的坐标为( )
A. B. C. D.
二、填空题(本大题共8小题,每小题4分,共32分)
11.(23-24八年级下·全国·假期作业)一个四边形的四条边的长度依次为a,b,c,d,且满足,则这个四边形一定是 .
12.(23-24八年级下·甘肃平凉·期中)如图,在四边形中,,添一个条件 ,使四边形是平行四边形.(不需作其它辅助线)
13.(2024·浙江宁波·模拟预测)在《圆锥曲线论》中有一个著名的“阿波罗尼奥斯定理”,这个定理可以表述为:平行四边形对角线的平方和等于各边的平方和. 如图,在中,,,,D是的中点,则的长为 .
14.(23-24八年级下·湖北孝感·期中)如图,两张对边平行的纸条随意交叉叠放在一起,重合部分构成一个四边形. 若, 则 .
15.(23-24八年级下·湖北黄冈·期中)在四边形中,,,,则 .
16.(2012·贵州黔西·中考真题)如图,在△ABC中,∠ACB=90°,D是BC的中点,DE⊥BC,CE//AD,若AC=2,CE=4,则四边形ACEB的周长为 .
17.(2024·辽宁·模拟预测)如图,在中,,连接,过点A作交的延长线于点E,过点E作交的延长线于点F,若,则 .
18.(21-22八年级下·北京朝阳·期末)已知直线及线段,点在直线上,点在直线外.如图.
(1)在直线上取一点(不与点重合),连接;
(2)以点为圆心,长为半径作弧,以点为圆心,长为半径作弧,两弧交于点(与点位于直线异侧);
(3)连接交于点,连接,.
根据以上作图过程及所作图形,在下列结论①;②;③中,一定正确的是 (填写所有正确的序号).
三、解答题(本大题共6小题,共58分)
19.(8分)19.(23-24九年级下·浙江杭州·期中)如图,已知,,.
(1)求证:;
(2)连接,那么相等吗?请说明理由.
20.(8分)(2024·湖南岳阳·一模)如图,点、、、在一条直线上,且,.
(1)求证:;
(2)求证:四边形是平行四边形.
21.(10分)(2024八年级下·北京·专题练习)如图,在平行四边形中,F是的中点,延长到点E.使,连接、.
(1)求证:;
(2)若,,.求的长.
22.(10分)(23-24八年级下·山东济南·期中)如图,中,E、F为对角线上的两点,且,连接,.
(1)求证:.
(2)连接、,求证:四边形是平行四边形.
23.(10分)(23-24八年级下·河南商丘·期中)如图,以的三边为边,在的同一侧分别作等边三角形,等边三角形,等边三角形,连接.
(1)判断四边形的形状,并证明你的结论.
(2)若,求的度数.
24.(12分)(22-23八年级下·北京海淀·期末)(1)探究规律:
已知:如图,点为平行四边形内一点, 、 的面积分别记为 、 ,平行四边形的面积记为,试探究与之间的关系.
(2)解决问题:
如图矩形中,,,点、、、分别在、、、上,且,.点为矩形内一点,四边形、四边形 的面积分别记为、,求.
中小学教育资源及组卷应用平台
试卷第1页,共3页
参考答案:
1.C
【分析】此题考查了平行四边形的判定,全等三角形的判定与性质,根据平行四边形的判定定理逐项判断即可,解题的关键是熟知平行四边形的判定定理.
【详解】、由可得,结合题意,不能证明四边形成为平行四边形,不符合题意;
、由,结合题意,不能证明四边形成为平行四边形,不符合题意;
、∵,
∴,
又,,
∴,
∴,
∴四边形是平行四边形,符合题意;
、由,结合题意,不能证明四边形成为平行四边形,不符合题意;
故选:.
2.C
【分析】本题考查了平行四边形的判定和性质以及三角形的面积.先判断四边形为平行四边形得到,则,再利用得到点和点到的距离相等,设点到的距离为,利用的面积为可计算出,然后根据平行四边形的面积公式计算四边形的面积.
【详解】解:,
四边形为平行四边形,
,
,
,
点和点到直线的距离相等,
设点到的距离为,
的面积为,
,
解得,
四边形的面积.
故选:C.
3.D
【分析】本题考查了平行四边形的判定与性质,熟练掌握平行四边形的判定与性质是解题关键.先判断出四边形是平行四边形,再根据平行四边形的性质求解即可得.
【详解】解:由题意得:,
∴四边形是平行四边形,
∴,
故选:D.
4.B
【分析】根据平行四边形的性质,,可得是等腰三角形,再根据,可得四边形是平行四边形,根据,由此即可求解.
【详解】解:∵四边形是平四边形,
∴,,
∵,
∴,
∵,
∴,
∴是等腰三角形,即,
∵,,点在的延长线上,
∴,
∴四边形是平行四边形,
∴,
∴,
∴,
故选:.
【点拨】本题主要考查平行四边形的判定和性质,等腰三角形的判定和性质的综合,掌握以上知识的综合运用是解题的关键.
5.C
【分析】利用平行四边形对角线互相平分,中线将三角形面积平分这一性质解题.
【详解】∵四边形ABCD是平行四边形,EF经过对角线交点O,
∴易得S△BEO=S△DFO,
∴S阴影部分=S△AOB=S ABCD
故选C.
【点拨】本题考查了平行四边形的面积,属于简单题,熟悉平行四边形性质和中线性质是解题关键.
6.B
【分析】本题考查了平行四边形的判定,在应用判定定理判定平行四边形时,应仔细观察题目所给的条件,仔细选择适合于题目的判定方法进行解答,避免混用判定方法.根据平行四边形的判定:两组对角分别相等的四边形是平行四边形,据此判断即可.
【详解】解:根据平行四边形的判定:两组对角分别相等的四边形是平行四边形,和是对角,和是对角,对角的份数应相等.只有选项B符合.
故选:B
7.B
【分析】此题主要考查了平行四边形的判定,解题的关键是掌握平行四边形的判定定理.根据平行四边形的判定定理分别进行分析即可.
【详解】解:A、,根据两组对边分别相等的四边形是平行四边形可判定四边形为平行四边形,故此选项不合题意;
B、,不能判定四边形是平行四边形,可能是等腰梯形,故此选项符合题意;
C、,根据两组对边分别平行的四边形是平行四边形可判定四边形为平行四边形,故此选项不合题意;
D、,根据一组对边平行且相等的四边形是平行四边形可判定四边形为平行四边形,故此选项不合题;
故选:B
8.D
【分析】根据已知判定四边形是平行四边形,得到,再根据三角形内角和定理求解.
【详解】解:∵,,
∴四边形是平行四边形,
∴,
∵,
∴,
故选:D.
【点拨】本题考查了平行四边形的判定和性质,三角形内角和,解题的关键是根据平行四边形得到.
9.D
【分析】先根据两组对边分别平行证明四边形是平行四边形,再根据两张纸条的宽度相等,利用面积求出,然后根据邻边相等的平行四边形是菱形即可证明;根据宽度是2与求出菱形的边长,然后利用菱形的面积底高计算即可.
【详解】解:纸条的对边平行,即,,
∴四边形是平行四边形,
过A作,垂足为E,
∵两张纸条的宽度都是2,
∴,
∵,
∴,
∴,
在中,,
即,
∴,负值舍去,
∴.
故选:D.
【点拨】本题考查了平行四边形的判定与性质,勾股定理,直角三角形的性质,解题的关键是根据勾股定理求出.
10.C
【分析】连接并延长交y轴于E,连接,求出的长度即可求解.
【详解】解:连接并延长交y轴于E,连接,
∵,
∴四边形是平行四边形,
∴x轴,,
∴y轴,
∵,
∴,
∴,
∴
∵,
∴,
∴点O的对应点的坐标为,
故选:C.
【点拨】本题考查了旋转的性质、含的直角三角形.掌握相关结论是解题关键.
11.平行四边形
【解析】略
12.(或或者)答案不唯一
【分析】本题考查了平行四边形的判定,是开放题,答案不唯一,利用平行四边形的判定方法来添加条件,平行四边形的判定方法共有五种,在四边形中如果有:1、四边形的两组对边分别平行,2、一组对边平行且相等,3、两组对边分别相等,4、对角线互相平分,5、两组对角分别相等.则四边形是平行四边形.
根据平行四边形的判定方法,可以再加一个:的条件,利用两组对边分别相等的四边形是平行四边形而得证.
【详解】解:根据平行四边形的判定,可添加:(答案不唯一).
故答案为:(或或).
13.
【分析】本题考查了平行四边形的判定和性质,熟练运用阿波罗尼奥斯定理是解题的关键.
延长到E,使,连接,,根据线段中点的定义得到,推出四边形是平行四边形,得到,,根据阿波罗尼奥斯定理解方程即可得出结论.
【详解】解:延长到E,使,连接,,
点D是的中点,
,
,
四边形是平行四边形,
,,
由阿波罗尼奥斯定理得:,
,
,
,
故答案为:.
14.8
【分析】本题主要考查平行四边形的判定和性质,掌握平行四边形的判定和性质是解题的关键.由条件可知,可证明四边形为平行四边形,可得到.
【详解】解:∵,
∴四边形为平行四边形,
∴.
故答案为:8
15./50度
【分析】本题考查平行四边形的判定和性质,解题的关键是熟练掌握基本知识,属于中考基础题.
证明四边形是平行四边形,再利用其性质即可解决问题
【详解】
解:,,
四边形是平行四边形,
,
,
,
故答案为:.
16./
【分析】先证明四边形ACED是平行四边形,可得DE=AC=2.由勾股定理和中线的定义可求AB和EB的长,从而求出四边形ACEB的周长.
【详解】∵∠ACB=90°,DE⊥BC,
∴AC∥DE.
又∵CE∥AD,
∴四边形ACED是平行四边形.
∴DE=AC=2.
在Rt△CDE中,DE= 2,CE=4,由勾股定理得.
∵D是BC的中点,
∴BC=2CD=4.
在△ABC中,∠ACB=90°,由勾股定理得.
∵D是BC的中点,DE⊥BC,
∴EB=EC=4.
∴四边形ACEB的周长=AC+CE+EB+BA=10+.
故答案为:10+.
17.
【分析】本题考查了平行四边形的判定与性质、含30度角的直角三角形的性质,熟练掌握平行四边形的判定与性质是解题关键.
先根据平行四边形的判定与性质可得四边形是平行四边形,根据平行四边形的性质可得,从而可得,再根据含30度角的直角三角形的性质可得,由此即可得.
【详解】解:∵四边形是平行四边形,,
∴,,
∵,
∴四边形是平行四边形,
∴,
∴,
∵,
∴,
∵,
∴,
∴,
∴,
故答案为:2.
18.①②/②①
【分析】
根据作图可得,则四边形是平行四边形,进而即可求解.
【详解】解:根据作图可得,则四边形是平行四边形,
∴,;故①②正确,
∵不一定相等,则不一定成立,即③不一定正确;
故答案为:①②.
【点拨】本题考查了平行四边形的性质与判定,熟练掌握基本作图以及平行四边形的性质与判定是解题的关键.
19.(1)见解析
(2)相等,见解析
【分析】本题考查全等三角形的判定与性质,平行线的判定与性质,平行四边形的判定与性质.
(1)由得,即,由得,进而可得,再用边角边证明其全等即可;
(2)由得,,故,得出四边形是平行四边形即可.
【详解】(1)证明:∵,
∴,即
∵,
∴,
∵,
∴
在和中
∴;
(2)解:相等.理由如下:
∵
∴,,
∴
∴四边形是平行四边形
∴.
20.(1)见解析
(2)见解析
【分析】本题考查了平行线的判定与性质,全等三角形的判定与性质,平行四边形的判定,解题关键是掌握全等三角形的判定与性质及平行四边形的判定方法.
(1)根据平行线的性质“两直线平行,内错角相等”得,再根据,等量交换得,结合已知条件,根据全等三角形判定(边角边),得,即可得;
(2)根据(1)得,由全等三角形的性质得,,根据平行线的判定“内错角相等,两直线平行”得,再根据平行四边形的判定“一组对边平行且相等的四边形是平行四边形”,即可证得结论.
【详解】(1)证明:,
,
又,
,
即,
在和中,
,
,
.
(2)证明:由(1)得,
,,
,
四边形是平行四边形.
21.(1)见解析
(2)
【分析】本题主要考查了平行四边形的判定以及性质,平行线的性质以及勾股定理解三角形等知识点.
(1)由平行四边形的性质得出,且,由中点的定义得出,结合已知条件即可得出,进一步证明四边形是平行四边形,再由平行四边形的性质可得出.
(2)过点C作于点H.由平行线的性质得出,则,由勾股定理求出,由平行四边形的性质得出,即可求出,再利用勾股定理即可求出.
【详解】(1)证明:∵四边形是平行四边形,
∴,且,
∵F是的中点,
∴,
又∵,
∴,
∵,
∴四边形是平行四边形,
∴;
(2)如图,过点C作于点H.
在中,,,
∴.
∵,,
∴,,
在中,,
∴,
∴,
由(1)可知,四边形是平行四边形,
∴,
∴,
在,根据勾股定理得:
.
22.(1)见解析
(2)见解析
【分析】本题主要考查了全等三角形的判定和性质,平行四边形的判定和性质,平行线的判定和性质,解题的关键是熟练掌握相关的判定和性质.
(1)根据四边形的性质得出,,证明,得出即可;
(2)根据,得出,,证明,即可证明结论.
【详解】(1)证明:∵四边形为平行四边形,
∴,,
∴,
在与中
,
∴,
∴.
(2)证明:连接、.
由(1)得,,
∴,,
∵,,
∴,
∴,
∴四边形为平行四边形.
23.(1)四边形是平行四边形,证明见详解
(2)
【分析】(1)根据等边三角形的性质推出,求出,证,推出,同理得出,即可得出结论.
(2)先根据等边三角形的性质,得出,结合周角概念列式,得出,根据平行四边形的性质,即可作答.
此题主要考查了等边三角形的性质和平行四边形的判定.
【详解】(1)证明:四边形是平行四边形,证明如下:
、、都是等边三角形,
,,,,
,
即,
在和中,
,
,
,
,
,
同理,
四边形是平行四边形.
(2)解:∵都是等边三角形,
∴
∵
∴
∵四边形是平行四边形.
∴.
24.(1),证明见解析;(2)
【分析】(1)如图所示,过点作,作延长线于点,延长交于点,可得平行四边形与同底同高,平行四边形与同底同高,由此即可求解;
(2)如图所示,连接、、、得四边形,可证,,即四边形是平行四边形,并可求出,,由此可求出平行四边形的面积,由(1)的计算方法即可求解.
【详解】证明:(1),理由如下,
如图所示,过点作,作延长线于点,延长交于点,
∵四边形是平行四边形,
∴,
∴,,,
∴,,,
∴,.
∵,
,
.
解:(2)如图所示,连接、、、得四边形,
∵四边形是矩形,
∴,,,
∵,,,
∴,
∴,且,
同理可得,,,,,,
∴四边形为平行四边形,,
∴,
由(1)可得,
∴.
【点拨】本题主要考查平行四边形的性质、矩形的性质及不规则图形面积的计算方法,掌握已知知识的综合运用是解题的关键.
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
