六年级上册数学人教版《扇形的认识》(课件)(共32张PPT)
文档属性
| 名称 | 六年级上册数学人教版《扇形的认识》(课件)(共32张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 14.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-27 09:24:10 | ||
图片预览







文档简介
(共32张PPT)
人教版小学数学六年级上册第五单元
学习目标
目标一
弧、圆心角、扇形的概念
目标二
扇形的大小与什么有关
目标三
能按要求画扇形,能准确求出扇形的面积和周长
复习巩固
扇贝
折扇
扇形藻
这些物体的名称都含有“扇”字,那什么是扇形呢?
这些物体的外形有什么相同的地方?
了解扇形
生活中处处都有扇形。
先自学73页再交流
1.什么是弧,弧怎么读、写?
2.什么是扇形,扇形的各部分的名称是什么?
3.扇形的大小和什么有关系?
完成时间2分钟
认识扇形
一起了解什么是扇形以及扇形的组成。
O
A
B
弧
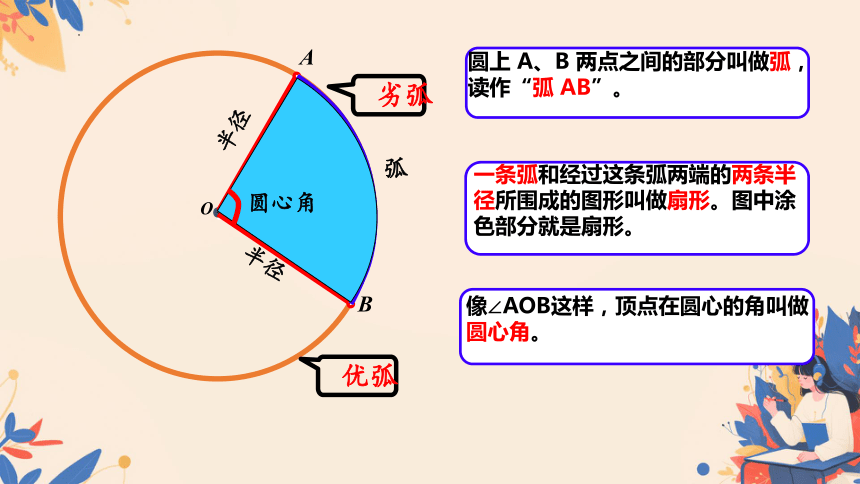
圆上 A、B 两点之间的部分叫做弧,读作“弧 AB”。
半径
半径
一条弧和经过这条弧两端的两条半径所围成的图形叫做扇形。图中涂色部分就是扇形。
圆心角
像∠AOB这样,顶点在圆心的角叫做圆心角。
劣弧
优弧
扇形
√
√
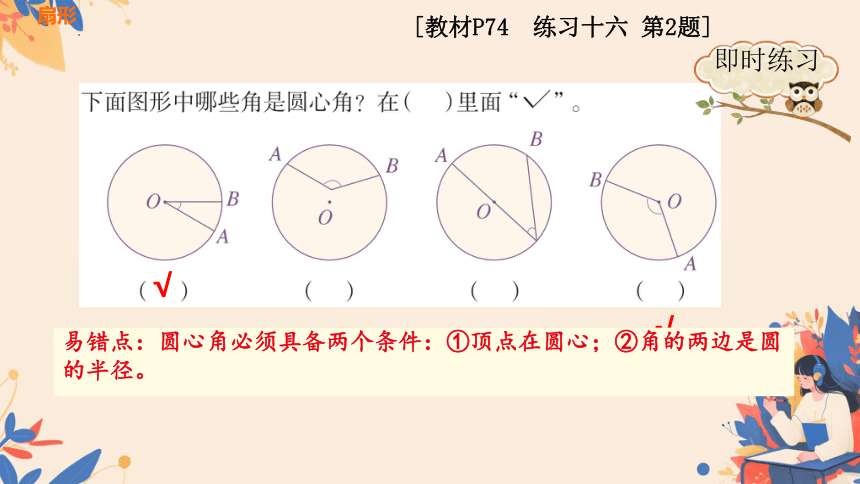
即时练习
[教材P74 练习十六 第2题]
易错点:圆心角必须具备两个条件:①顶点在圆心;②角的两边是圆的半径。
先画一个半径是2cm的圆,再在圆中画一个圆心角是100O的扇形。
活动要求:
1.借助圆规和量角器;
2.标出圆心O和弧的两端A、B。
3.标记清楚其中的弧、半径和圆心角。
完成时间2分钟
[教材P74 练习十六 第3题]
r=2cm
100°
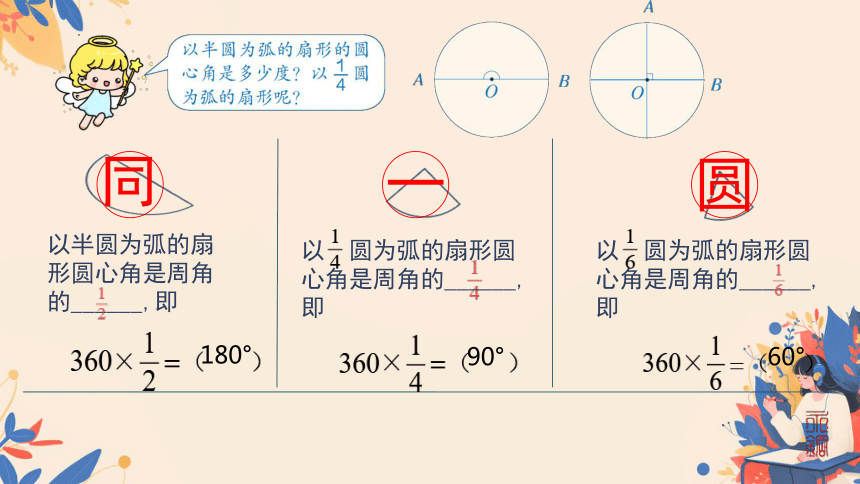
以半圆为弧的扇形圆心角是周角的______,即
以 圆为弧的扇形圆心角是周角的______,即
以 圆为弧的扇形圆心角是周角的______,即
一
圆
同
180°
90°
60°
比较下面图形中扇形的大小,你有什么发现?
在同一个圆里,圆心角越大,所对应的扇形越大;圆心角越小,所对应的扇形越小。
圆心角相同的扇形,半径越长,扇形越大
圆心角一样大,扇形就一定一样大吗?
扇形的大小和圆心角、半径都有关。
扇形的大小与什么有关?
小结
在同一个圆中(半径不变),圆心角越大,扇形(面积)就越大
圆心角不变,半径越大,扇形(面积)越大。
1条
扇形有几条对称轴?
归纳:扇形是轴对称图形,它只有一条对称轴。通过扇形圆心和弧中点的直线就是扇形的对称轴。
扇形周长=弧长+2条半径
如何求扇形的周长?
90O
180O
270O
90O
180O
270O
如何求扇形的面积?
知识扩展
你会计算扇形的面积吗?
下面圆中的扇形面积各是圆面积的几分之几?并说明理由。
270
36
120
扇形面积公式:
扇形的面积
A
B
O
r
圆心角为n0的扇形面积是圆面积的 。
圆的面积为 。
求扇形的面积。
A
B
O
你会求扇形的面积吗?
归纳:
扇形的周长=弧长+半径×2
1. 指出下列物体中的扇形。
[教材P74 练习十六 第1题]
巩固运用,拓展深化
巩固练习
3.下面各图中阴影部分的图形是扇形吗?说出你的理由。
4.下面图形中的扇形是几分之几的圆?
你在生活中见过下面这些图案吗?
[教材P74 练习十六 第4题]
拓展延伸,认识扇环
像下面这样一个圆环被截得的部分叫作扇环。你能求出下面各扇环的面积吗?
大扇形面积-小扇形面积
S扇环=
观察发现,这个图形是有两个扇环组成
旋转下面的扇环,与上面的扇环,拼接在一起,就成了一个半圆形的扇环
原来的图形面积,就是这个扇环的面积
扇环的面积等于大扇形(大半圆)的面积减去小扇形(小半圆)的面积
1dm
r=4dm
大圆半径是4dm,大扇形面积是:3.14×4 ÷2=25.12dm
小圆半径是(4-1)=3dm,小扇形面积是:3.14×3 ÷2=14.13dm
扇环面积:25.12-14.13=10.99dm
S扇环=
小结
半径
半径
弧
圆心角
课后作业
完成练习册本课时的习题。
人教版小学数学六年级上册第五单元
学习目标
目标一
弧、圆心角、扇形的概念
目标二
扇形的大小与什么有关
目标三
能按要求画扇形,能准确求出扇形的面积和周长
复习巩固
扇贝
折扇
扇形藻
这些物体的名称都含有“扇”字,那什么是扇形呢?
这些物体的外形有什么相同的地方?
了解扇形
生活中处处都有扇形。
先自学73页再交流
1.什么是弧,弧怎么读、写?
2.什么是扇形,扇形的各部分的名称是什么?
3.扇形的大小和什么有关系?
完成时间2分钟
认识扇形
一起了解什么是扇形以及扇形的组成。
O
A
B
弧
圆上 A、B 两点之间的部分叫做弧,读作“弧 AB”。
半径
半径
一条弧和经过这条弧两端的两条半径所围成的图形叫做扇形。图中涂色部分就是扇形。
圆心角
像∠AOB这样,顶点在圆心的角叫做圆心角。
劣弧
优弧
扇形
√
√
即时练习
[教材P74 练习十六 第2题]
易错点:圆心角必须具备两个条件:①顶点在圆心;②角的两边是圆的半径。
先画一个半径是2cm的圆,再在圆中画一个圆心角是100O的扇形。
活动要求:
1.借助圆规和量角器;
2.标出圆心O和弧的两端A、B。
3.标记清楚其中的弧、半径和圆心角。
完成时间2分钟
[教材P74 练习十六 第3题]
r=2cm
100°
以半圆为弧的扇形圆心角是周角的______,即
以 圆为弧的扇形圆心角是周角的______,即
以 圆为弧的扇形圆心角是周角的______,即
一
圆
同
180°
90°
60°
比较下面图形中扇形的大小,你有什么发现?
在同一个圆里,圆心角越大,所对应的扇形越大;圆心角越小,所对应的扇形越小。
圆心角相同的扇形,半径越长,扇形越大
圆心角一样大,扇形就一定一样大吗?
扇形的大小和圆心角、半径都有关。
扇形的大小与什么有关?
小结
在同一个圆中(半径不变),圆心角越大,扇形(面积)就越大
圆心角不变,半径越大,扇形(面积)越大。
1条
扇形有几条对称轴?
归纳:扇形是轴对称图形,它只有一条对称轴。通过扇形圆心和弧中点的直线就是扇形的对称轴。
扇形周长=弧长+2条半径
如何求扇形的周长?
90O
180O
270O
90O
180O
270O
如何求扇形的面积?
知识扩展
你会计算扇形的面积吗?
下面圆中的扇形面积各是圆面积的几分之几?并说明理由。
270
36
120
扇形面积公式:
扇形的面积
A
B
O
r
圆心角为n0的扇形面积是圆面积的 。
圆的面积为 。
求扇形的面积。
A
B
O
你会求扇形的面积吗?
归纳:
扇形的周长=弧长+半径×2
1. 指出下列物体中的扇形。
[教材P74 练习十六 第1题]
巩固运用,拓展深化
巩固练习
3.下面各图中阴影部分的图形是扇形吗?说出你的理由。
4.下面图形中的扇形是几分之几的圆?
你在生活中见过下面这些图案吗?
[教材P74 练习十六 第4题]
拓展延伸,认识扇环
像下面这样一个圆环被截得的部分叫作扇环。你能求出下面各扇环的面积吗?
大扇形面积-小扇形面积
S扇环=
观察发现,这个图形是有两个扇环组成
旋转下面的扇环,与上面的扇环,拼接在一起,就成了一个半圆形的扇环
原来的图形面积,就是这个扇环的面积
扇环的面积等于大扇形(大半圆)的面积减去小扇形(小半圆)的面积
1dm
r=4dm
大圆半径是4dm,大扇形面积是:3.14×4 ÷2=25.12dm
小圆半径是(4-1)=3dm,小扇形面积是:3.14×3 ÷2=14.13dm
扇环面积:25.12-14.13=10.99dm
S扇环=
小结
半径
半径
弧
圆心角
课后作业
完成练习册本课时的习题。
