北师大版小学数学三年级下册 总复习 课件(共82张PPT)
文档属性
| 名称 | 北师大版小学数学三年级下册 总复习 课件(共82张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 31.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-27 00:00:00 | ||
图片预览









文档简介
(共82张PPT)
北师大版小学数学三年级下册
总复习
数的运算
复习导入
数 的 运 算
1、说一说与日常生活密切相关的数。
整数除法的计算法则:
1、从最高位除起
2、除到被除数的哪一位,就在哪一位上写上商;
3、每次除得的余数必须比除数小。
判断商是几位数
被除数百位上的数 ≥ 除数
商三位数
被除数百位上的数 < 除数
商两位数
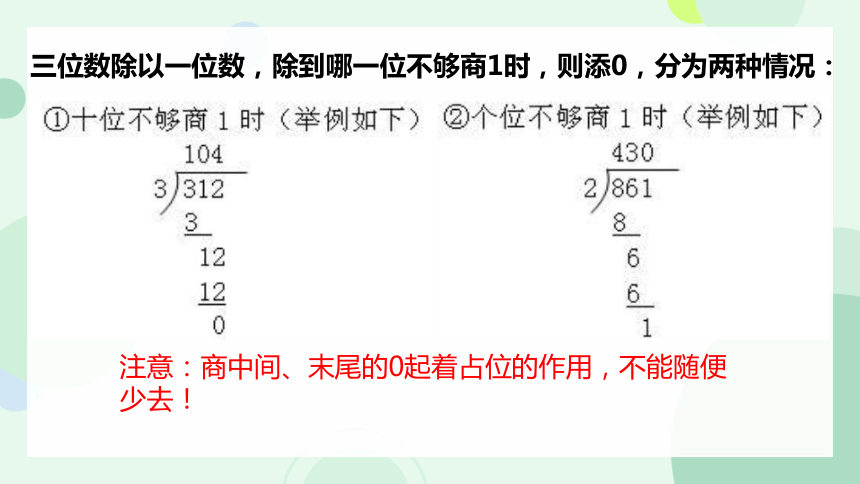
注意:商中间、末尾的0起着占位的作用,不能随便少去!
三位数除以一位数,除到哪一位不够商1时,则添0,分为两种情况:
除法的估算:在实际生活中有时候不必算出准确的结果,而是把一些数看成和它接近的整十、整百、整千,然后进行计算,这样的计算就叫做估算。
除法估算举例:312÷3≈300÷3=100
除法的验算:
能除尽:被除数=商×除数
有余数:被除数=商×除数+余数
计算时要养成先估算,再计算,最后再验算的好习惯。
例:①甲是176,乙是甲的6倍,乙是多少?(“的”字左边的“甲”已知时,用“乘法”)
乙:176×6
②甲是1584,是乙的6倍,乙是多少?(“的”字左边的“乙”未知时,用“除法”)
乙:1584÷6
辨析容易混淆的文字题:
6 乘除法混合运算法则:
①算式里只有乘除法,要依次计算。
②一个数连续除以另外两个数,相当于除以那两个数的乘积。
例如:200÷2÷4=200÷(2×4)。
数的运算
0和1的运算
任何数加0得原数,任何数减0得原数。
0乘任何数得0,
0除以任何非0的数得0,0不能作除数。
任何数乘1得原数,任何数除以1得原数。
1 两位数乘两位数,积可能是(三)位数,也可能是(四)位数。
2 口算乘法:
整十、整百的数相乘,只需把前面数字相乘,再看两个乘数一 共有几个0,就在结果后面添上几个0。
3 两位数乘整十数的计算方法:
直接用两位数乘以整十数十位上的数,然后在乘积末尾加0即 可。
例如:23×50=? 先用23×5=115,再在115后面添0,得到 23×50=1150。
4 两位数乘两位数的竖式计算方法:
43×54=?
5 估算:
在实际生活中有时候不必算出准确的结果,而是把一些数看成和它接近的整十、整百、整千,然后进行计算,这样的计算就叫做估算。估算时,横式要写“≈”(约等号),答句中要加上“大约”。
如:估算18×22,可以先把因数看成整十、整百的数,再去计算。
(可以把一个乘数看成近似数,也可以把两个乘数都同时看成近似数。)
6 凡是问够不够,能不能等的题目,都要三大步:
①计算、②比较、③答题。
别忘了比较这一步。
7 笔算乘法:
先把第一个乘数同第二个乘数个位上的数相乘,再与第二个乘数十位上的数相乘。
8 相关公式:
乘数×乘因数=积
积÷乘数=另一个乘数
9 运算顺序:
先乘除,再算加减;
同级运算,应按从左到右的顺序进行计算;
如果有括号,要先算括号内的运算。
10 乘法计算规律:
一个乘数不变,另一个乘数扩大若干倍,积也扩大相同的倍数。
例如:23×4=92,若23这个乘数不变,另一个乘数4扩大10倍,则积也扩大10倍,为920。
小数加法的计算方法:
1、把小数点对齐,从低位加起,
2、哪一位上的数相加满十,就向前一位进1,
点上小数点。
小数减法的计算方法:
1、把小数点对齐,从低位减起,
2、被减数的小数末尾位数不够,可以添“0”再 减。
3、哪一位上的数不够减,要从前一位退1,在本 位加十再减。
小数
1、分数的意义:
把一个整体平均分成若干份,表示其中的几份就是这个整体的几分之几,所分的份数作分母,所占的份数作分子。
认识几分之一:把一个整体平均分成几份,每一份就是它的几分之一。
认识几分之几:把一个整体平均分成几份,取其中的几份,就是这个整体的几分之几。
把一个整体平均分得的份数越多,它的每一份所表示的数就越小。
2、比较大小的方法:
分子相同比分母,分母小的分数反而大,分母大的分数反而小。
分母相同比分子,分子大的分数就大,分子小的分数就小。
3、分数加、减法:
① 同分母分数相加、减法的计算方法:分母不变,分子相加减;
② 1减几分之几的计算方法:计算1减几分之几时,先把1写成与减数分母相同的分数(1可以看作是分子分母相同的分数),再计算。
4、请分别画图表示 和 ,并画一画、说一说如何
计算 , 。
分母相同的分数,( )
分子相同的分数,( )
3、举例说一说怎样比较分数的大小。
复习乘法、除法和四则混合运算:
有乘法又有加减法,先算( )再算( )
有除法又有加减法,先算( )再算( )
只有乘除法要按照( )的次序进行计算。
只有加减法要按照( )的次序进行计算。
有括号的要先算括号( ),再算括号( )。
(1)根据下图,你能提出哪些数学问题?与同伴说一说。
(2)在解决问题的过程中,你使用了哪些运算?
小小商店
90个
45个
一共进了200个球。
进的足球有多少个?
90+45=
135(个)
200-135=
65(个)
答:进的足球有65个。
运用了加法和减法运算。
(答案不唯一)
2.
(1)根据下图,你能提出哪些数学问题?与同伴说一说。
(2)在解决问题的过程中,你使用了哪些运算?
植 树
有15行,每行32棵树。
一共有多少棵树?
15×32=
480(棵)
答:一共有480棵树。
运用了乘法运算。
(答案不唯一)
2.
(1)根据下图,你能提出哪些数学问题?与同伴说一说。
(2)在解决问题的过程中,你使用了哪些运算?
装鸡蛋
平均每篮装多少个鸡蛋?
150÷2=
75(个)
答:平均每篮装75个鸡蛋。
150个
运用了除法运算。
(答案不唯一)
2.
14×12=
14×2=28
14×10=140
140+28=168
168
693÷3=
231
(1). 圈一圈,算一算,说一说你是怎样计的?
(2)算一算,说一说为什么小数点要对齐。
3 . 2
+ 4 . 5
7 . 8
+ 1 2 . 6
1 9 . 2
- 7 . 2
5
- 1 . 9
元 角
元 角
元 角
元 角
7
7
.
4
0
.
2
0
2
.
1
0
1
.
3
.
(3)涂一涂,算一算。
5.(1)先画图理解题意,再解决问题。
每条12元
应该找回多少元?
我买3条。
100元
12×3=
36(元)
100-36=64(元)
答:应该找回64元。
5.(1)先画图理解题意,再解决问题。
它们一共收了多少个?
180-20=
160(个)
180+160=340(个)
答:它们一共收了340个。
我收了180个。
我收的比你少20个。
5.(1)先画图理解题意,再解决问题。
平均每行站多少人?
72÷2=
36(人)
36÷6=6(人)
答:平均每行站6人。
一共有72人,平均分成2个方阵。
每个方阵有6行。
解决问题的一般步骤
(1)审清题意,并找出已知条件和所求问题;
(2)分析数量关系,确定先算什么,再算什 么,最后算什么;
(3)列式计算;
(4)检验并写出答。
数的运算
算一算。
240×2÷6 840÷4×3 128+18×6
300-129÷3 (128+132)÷5 312×(300-296)
=480÷6
=80
=210×3
=630
=300-43
=257
=260÷5
=52
=128+108
=236
=312×4
=1248
数的运算
门票
每张3元
97名学生去公园,带300元买门票够不够?
求97名学生需要多少钱?
97×3=291(元)
291<300
答:带300元买门票够。
数的运算
学校成立了“红领巾爱心捐助站”。第一周同学们
捐献课外书56本,第二周捐献的比第一周的2倍还多
14本,第二周同学们捐献了多少本课外书?
先求第一周的2倍是多少,
然后再加上14本。
56×2+14
=112+14
答:第二周同学们捐献了126本课外书。
=126(本)
数的运算
为了参加溜溜球比赛,王老师买了4盒溜溜球,每盒2个,
一共花了96元,平均每个溜溜球多少元
方法一:
先求出平均每盒溜溜球多少元?
求平均每个溜溜球多
少元?
96÷4=24(元)
24÷2=12(元)
答:平均每个溜溜球12元。
96÷4÷2
=24÷2
=12(元)
数的运算
方法二:
先求出4盒溜溜球一共有多少个?
求平均每个溜溜球多
少元?
2×4=8(个)
96÷8=12(元)
96÷(2×4)
=96÷8
=12(元)
为了参加溜溜球比赛,王老师买了4盒溜溜球,每盒2个,一共花了96元,平均每个溜溜球多少元
答:平均每个溜溜球12元。
数的运算
买7个文具盒需要多少钱?
36÷3=12(元)
答:买7个文具盒需要84元钱。
12×7=84(元)
两位老师带领53名同学到公园划船,
每条大船可以坐6人,租金60元;每条小船可以坐4人,租金48元。
小组合作,请至少写出4种租船方案,并比较它们的租金。
9
1
9×6+4=58
9×60+48=588
8
2
8×6+2×4=56
8×60+2×48=576
7
3
7×6+4×3=54
7×60+3×48=564
6
5
6×6+5×4=56
6×60+5×48=600
因为564<576<588<600,所以方案三最省钱。
常 见 的 量
2012年伦敦奥运会上,16岁的叶诗文在女子400米混合泳决赛中,以4分28秒43的成绩夺得冠军,并打破世界纪录。
周璐璐在女子75千克以上举重决赛中,以333千克的总成绩打破了世界纪录,摘得金牌。
上面的信息中有哪些量?哪些是质量单位?哪些是……
举例说明4分大约有多长,300千克大约有多重.
你还知道哪些关于时间、人民币和质量单位?举例说一说。
常见的质量单位:
我们学过质量单位( )。
相邻的质量单位的进率是( )。
你知道质量单位如何用字母表示吗?
常见的人民币单位
我们学过人民币单位( )。
相邻的人民币单位的进率是( )。
常见的时间单位
我们学过时间单位( )。
相邻的时间单位的进率是( )。
你还知道哪些时间单位?
“年、月、日”的知识
年、月、日
1年12个月
大月:31天
小月:30天
特殊月:28天或29天
平年、闰年
计时法:
普通计时法
24时计时法
+12
-12
经过时间
数:在钟表上数一数
计算
一三五七八十腊,
三十一天永不差,
平年二月二十八,
闰年二月把一加。
采 蘑 菇
平年
上午8时( ) 晚上9时 ( )
早上7时半( ) 下午2时20分( )
16时( ) 23时50分( )
6时 ( ) 15时15分 ( )
(1)火车6:34从北京开出,10:49到沈阳, 经过 ( )分。
(2)一场足球赛从14时30分开始,经过100分 钟,结束时间是( )。
图形的认识
图形与测量
1、面积定义:
物体的表面或封闭图形的大小,就是它们的面积。
封闭图形一周的长度叫周长。
长度单位和面积单位的单位不同,无法比较。
2、认识面积单位:
平方米 (m ) 平方分米(dm ) 平方厘米(cm )
3、面积单位的换算
1平方米=100 平方分米
1平方分米=100平方厘米
1平方厘米=100平方毫米
1平方米=10000 平方厘米
相邻两个常用的面积单位之间的进率是100。
4、测量与比较
① 比较两个图形面积的大小,要用统一的面积单位来测量。
② 区分长度单位和面积单位的不同:长度单位测量线段的长短,面积单位测量面的大小。
③ 在生活中找出接近于1平方厘米、1平方分米、1平方米的例子。如1平方厘米(指甲盖)、1平方分米(电线插座)、1平方米(黑板一面)。
④ 周长相等的两个长方形,面积不一定相等。
⑤ 面积相等的两个长方形,周长也不一定相等。
5、长方形:
长方形的面积=长×宽
长方形的周长=(长+宽)×2
求长:长=长方形面积÷宽
已知周长求长:
长=长方形周长÷2-宽
求宽:宽=长方形面积÷长
已知周长求宽:
宽=长方形周长÷2-长
6、正方形:
正方形的面积=边长×边长
正方形的周长=边长×4
边长=正方形面积÷边长
已知周长求边长=正方形周长÷4
图形的运动
1 轴对称图形:
对折后两边能完全重合的图形是轴对称图形。
2 对称轴:
对折后能使两边重合的线叫做对称轴。
3 轴对称图形特点:
对称轴是一条直线,对称轴两侧的对应点到对称轴两侧的距离相等,沿对称轴将它对折,左右两边完全重合。
4 轴对称图形的有:
角、五角星、等腰三角形、等边三角形、等腰梯形、正方形、长方形、圆和正多边形等都是轴对称图形等.
5 有的轴对称图形有不止一条对称轴:
圆有无数条对称轴,每条圆的直径所在的直线都是圆的对称轴.
6 既不是轴对称图形又不是中心对称图形有:
不等边三角形,非等腰梯形等
7 平移:
是指在平面内,将一个图形上的所有点都按照某个方向作相同距离的移动,这样的图形运动叫做图形的平移运动,简称平移。平移不改变图形的形状和大小。图形经过平移,对应线段相等,对应角相等,对应点所连的线段相等。
8 平移的特征:
图形平移前后的形状和大小没有变化,只是位置发生变化。
9 对平移和旋转现象的初步认识:
①张叔叔在笔直的公路上开车,方向盘的运动是(旋转)现象。
②升国旗时,国旗的升降运动是(平移)现象。
③妈妈用拖布擦地,是(平移)现象。
④自行车的车轮转了一圈又一圈是(旋转)现象。
10 镜子内外的左右方向是相反的。
统 计
数据的整理和表示
1、对调查数据的整理和表示:
可以通过写“正”字或者画条形图的方式。
2、信息应用:
可以通过数据统计得到哪个选项得票最多或最少,从而决定该怎样选择。还可以知道任意两个选项的得票数量差。
北师大版小学数学三年级下册
总复习
数的运算
复习导入
数 的 运 算
1、说一说与日常生活密切相关的数。
整数除法的计算法则:
1、从最高位除起
2、除到被除数的哪一位,就在哪一位上写上商;
3、每次除得的余数必须比除数小。
判断商是几位数
被除数百位上的数 ≥ 除数
商三位数
被除数百位上的数 < 除数
商两位数
注意:商中间、末尾的0起着占位的作用,不能随便少去!
三位数除以一位数,除到哪一位不够商1时,则添0,分为两种情况:
除法的估算:在实际生活中有时候不必算出准确的结果,而是把一些数看成和它接近的整十、整百、整千,然后进行计算,这样的计算就叫做估算。
除法估算举例:312÷3≈300÷3=100
除法的验算:
能除尽:被除数=商×除数
有余数:被除数=商×除数+余数
计算时要养成先估算,再计算,最后再验算的好习惯。
例:①甲是176,乙是甲的6倍,乙是多少?(“的”字左边的“甲”已知时,用“乘法”)
乙:176×6
②甲是1584,是乙的6倍,乙是多少?(“的”字左边的“乙”未知时,用“除法”)
乙:1584÷6
辨析容易混淆的文字题:
6 乘除法混合运算法则:
①算式里只有乘除法,要依次计算。
②一个数连续除以另外两个数,相当于除以那两个数的乘积。
例如:200÷2÷4=200÷(2×4)。
数的运算
0和1的运算
任何数加0得原数,任何数减0得原数。
0乘任何数得0,
0除以任何非0的数得0,0不能作除数。
任何数乘1得原数,任何数除以1得原数。
1 两位数乘两位数,积可能是(三)位数,也可能是(四)位数。
2 口算乘法:
整十、整百的数相乘,只需把前面数字相乘,再看两个乘数一 共有几个0,就在结果后面添上几个0。
3 两位数乘整十数的计算方法:
直接用两位数乘以整十数十位上的数,然后在乘积末尾加0即 可。
例如:23×50=? 先用23×5=115,再在115后面添0,得到 23×50=1150。
4 两位数乘两位数的竖式计算方法:
43×54=?
5 估算:
在实际生活中有时候不必算出准确的结果,而是把一些数看成和它接近的整十、整百、整千,然后进行计算,这样的计算就叫做估算。估算时,横式要写“≈”(约等号),答句中要加上“大约”。
如:估算18×22,可以先把因数看成整十、整百的数,再去计算。
(可以把一个乘数看成近似数,也可以把两个乘数都同时看成近似数。)
6 凡是问够不够,能不能等的题目,都要三大步:
①计算、②比较、③答题。
别忘了比较这一步。
7 笔算乘法:
先把第一个乘数同第二个乘数个位上的数相乘,再与第二个乘数十位上的数相乘。
8 相关公式:
乘数×乘因数=积
积÷乘数=另一个乘数
9 运算顺序:
先乘除,再算加减;
同级运算,应按从左到右的顺序进行计算;
如果有括号,要先算括号内的运算。
10 乘法计算规律:
一个乘数不变,另一个乘数扩大若干倍,积也扩大相同的倍数。
例如:23×4=92,若23这个乘数不变,另一个乘数4扩大10倍,则积也扩大10倍,为920。
小数加法的计算方法:
1、把小数点对齐,从低位加起,
2、哪一位上的数相加满十,就向前一位进1,
点上小数点。
小数减法的计算方法:
1、把小数点对齐,从低位减起,
2、被减数的小数末尾位数不够,可以添“0”再 减。
3、哪一位上的数不够减,要从前一位退1,在本 位加十再减。
小数
1、分数的意义:
把一个整体平均分成若干份,表示其中的几份就是这个整体的几分之几,所分的份数作分母,所占的份数作分子。
认识几分之一:把一个整体平均分成几份,每一份就是它的几分之一。
认识几分之几:把一个整体平均分成几份,取其中的几份,就是这个整体的几分之几。
把一个整体平均分得的份数越多,它的每一份所表示的数就越小。
2、比较大小的方法:
分子相同比分母,分母小的分数反而大,分母大的分数反而小。
分母相同比分子,分子大的分数就大,分子小的分数就小。
3、分数加、减法:
① 同分母分数相加、减法的计算方法:分母不变,分子相加减;
② 1减几分之几的计算方法:计算1减几分之几时,先把1写成与减数分母相同的分数(1可以看作是分子分母相同的分数),再计算。
4、请分别画图表示 和 ,并画一画、说一说如何
计算 , 。
分母相同的分数,( )
分子相同的分数,( )
3、举例说一说怎样比较分数的大小。
复习乘法、除法和四则混合运算:
有乘法又有加减法,先算( )再算( )
有除法又有加减法,先算( )再算( )
只有乘除法要按照( )的次序进行计算。
只有加减法要按照( )的次序进行计算。
有括号的要先算括号( ),再算括号( )。
(1)根据下图,你能提出哪些数学问题?与同伴说一说。
(2)在解决问题的过程中,你使用了哪些运算?
小小商店
90个
45个
一共进了200个球。
进的足球有多少个?
90+45=
135(个)
200-135=
65(个)
答:进的足球有65个。
运用了加法和减法运算。
(答案不唯一)
2.
(1)根据下图,你能提出哪些数学问题?与同伴说一说。
(2)在解决问题的过程中,你使用了哪些运算?
植 树
有15行,每行32棵树。
一共有多少棵树?
15×32=
480(棵)
答:一共有480棵树。
运用了乘法运算。
(答案不唯一)
2.
(1)根据下图,你能提出哪些数学问题?与同伴说一说。
(2)在解决问题的过程中,你使用了哪些运算?
装鸡蛋
平均每篮装多少个鸡蛋?
150÷2=
75(个)
答:平均每篮装75个鸡蛋。
150个
运用了除法运算。
(答案不唯一)
2.
14×12=
14×2=28
14×10=140
140+28=168
168
693÷3=
231
(1). 圈一圈,算一算,说一说你是怎样计的?
(2)算一算,说一说为什么小数点要对齐。
3 . 2
+ 4 . 5
7 . 8
+ 1 2 . 6
1 9 . 2
- 7 . 2
5
- 1 . 9
元 角
元 角
元 角
元 角
7
7
.
4
0
.
2
0
2
.
1
0
1
.
3
.
(3)涂一涂,算一算。
5.(1)先画图理解题意,再解决问题。
每条12元
应该找回多少元?
我买3条。
100元
12×3=
36(元)
100-36=64(元)
答:应该找回64元。
5.(1)先画图理解题意,再解决问题。
它们一共收了多少个?
180-20=
160(个)
180+160=340(个)
答:它们一共收了340个。
我收了180个。
我收的比你少20个。
5.(1)先画图理解题意,再解决问题。
平均每行站多少人?
72÷2=
36(人)
36÷6=6(人)
答:平均每行站6人。
一共有72人,平均分成2个方阵。
每个方阵有6行。
解决问题的一般步骤
(1)审清题意,并找出已知条件和所求问题;
(2)分析数量关系,确定先算什么,再算什 么,最后算什么;
(3)列式计算;
(4)检验并写出答。
数的运算
算一算。
240×2÷6 840÷4×3 128+18×6
300-129÷3 (128+132)÷5 312×(300-296)
=480÷6
=80
=210×3
=630
=300-43
=257
=260÷5
=52
=128+108
=236
=312×4
=1248
数的运算
门票
每张3元
97名学生去公园,带300元买门票够不够?
求97名学生需要多少钱?
97×3=291(元)
291<300
答:带300元买门票够。
数的运算
学校成立了“红领巾爱心捐助站”。第一周同学们
捐献课外书56本,第二周捐献的比第一周的2倍还多
14本,第二周同学们捐献了多少本课外书?
先求第一周的2倍是多少,
然后再加上14本。
56×2+14
=112+14
答:第二周同学们捐献了126本课外书。
=126(本)
数的运算
为了参加溜溜球比赛,王老师买了4盒溜溜球,每盒2个,
一共花了96元,平均每个溜溜球多少元
方法一:
先求出平均每盒溜溜球多少元?
求平均每个溜溜球多
少元?
96÷4=24(元)
24÷2=12(元)
答:平均每个溜溜球12元。
96÷4÷2
=24÷2
=12(元)
数的运算
方法二:
先求出4盒溜溜球一共有多少个?
求平均每个溜溜球多
少元?
2×4=8(个)
96÷8=12(元)
96÷(2×4)
=96÷8
=12(元)
为了参加溜溜球比赛,王老师买了4盒溜溜球,每盒2个,一共花了96元,平均每个溜溜球多少元
答:平均每个溜溜球12元。
数的运算
买7个文具盒需要多少钱?
36÷3=12(元)
答:买7个文具盒需要84元钱。
12×7=84(元)
两位老师带领53名同学到公园划船,
每条大船可以坐6人,租金60元;每条小船可以坐4人,租金48元。
小组合作,请至少写出4种租船方案,并比较它们的租金。
9
1
9×6+4=58
9×60+48=588
8
2
8×6+2×4=56
8×60+2×48=576
7
3
7×6+4×3=54
7×60+3×48=564
6
5
6×6+5×4=56
6×60+5×48=600
因为564<576<588<600,所以方案三最省钱。
常 见 的 量
2012年伦敦奥运会上,16岁的叶诗文在女子400米混合泳决赛中,以4分28秒43的成绩夺得冠军,并打破世界纪录。
周璐璐在女子75千克以上举重决赛中,以333千克的总成绩打破了世界纪录,摘得金牌。
上面的信息中有哪些量?哪些是质量单位?哪些是……
举例说明4分大约有多长,300千克大约有多重.
你还知道哪些关于时间、人民币和质量单位?举例说一说。
常见的质量单位:
我们学过质量单位( )。
相邻的质量单位的进率是( )。
你知道质量单位如何用字母表示吗?
常见的人民币单位
我们学过人民币单位( )。
相邻的人民币单位的进率是( )。
常见的时间单位
我们学过时间单位( )。
相邻的时间单位的进率是( )。
你还知道哪些时间单位?
“年、月、日”的知识
年、月、日
1年12个月
大月:31天
小月:30天
特殊月:28天或29天
平年、闰年
计时法:
普通计时法
24时计时法
+12
-12
经过时间
数:在钟表上数一数
计算
一三五七八十腊,
三十一天永不差,
平年二月二十八,
闰年二月把一加。
采 蘑 菇
平年
上午8时( ) 晚上9时 ( )
早上7时半( ) 下午2时20分( )
16时( ) 23时50分( )
6时 ( ) 15时15分 ( )
(1)火车6:34从北京开出,10:49到沈阳, 经过 ( )分。
(2)一场足球赛从14时30分开始,经过100分 钟,结束时间是( )。
图形的认识
图形与测量
1、面积定义:
物体的表面或封闭图形的大小,就是它们的面积。
封闭图形一周的长度叫周长。
长度单位和面积单位的单位不同,无法比较。
2、认识面积单位:
平方米 (m ) 平方分米(dm ) 平方厘米(cm )
3、面积单位的换算
1平方米=100 平方分米
1平方分米=100平方厘米
1平方厘米=100平方毫米
1平方米=10000 平方厘米
相邻两个常用的面积单位之间的进率是100。
4、测量与比较
① 比较两个图形面积的大小,要用统一的面积单位来测量。
② 区分长度单位和面积单位的不同:长度单位测量线段的长短,面积单位测量面的大小。
③ 在生活中找出接近于1平方厘米、1平方分米、1平方米的例子。如1平方厘米(指甲盖)、1平方分米(电线插座)、1平方米(黑板一面)。
④ 周长相等的两个长方形,面积不一定相等。
⑤ 面积相等的两个长方形,周长也不一定相等。
5、长方形:
长方形的面积=长×宽
长方形的周长=(长+宽)×2
求长:长=长方形面积÷宽
已知周长求长:
长=长方形周长÷2-宽
求宽:宽=长方形面积÷长
已知周长求宽:
宽=长方形周长÷2-长
6、正方形:
正方形的面积=边长×边长
正方形的周长=边长×4
边长=正方形面积÷边长
已知周长求边长=正方形周长÷4
图形的运动
1 轴对称图形:
对折后两边能完全重合的图形是轴对称图形。
2 对称轴:
对折后能使两边重合的线叫做对称轴。
3 轴对称图形特点:
对称轴是一条直线,对称轴两侧的对应点到对称轴两侧的距离相等,沿对称轴将它对折,左右两边完全重合。
4 轴对称图形的有:
角、五角星、等腰三角形、等边三角形、等腰梯形、正方形、长方形、圆和正多边形等都是轴对称图形等.
5 有的轴对称图形有不止一条对称轴:
圆有无数条对称轴,每条圆的直径所在的直线都是圆的对称轴.
6 既不是轴对称图形又不是中心对称图形有:
不等边三角形,非等腰梯形等
7 平移:
是指在平面内,将一个图形上的所有点都按照某个方向作相同距离的移动,这样的图形运动叫做图形的平移运动,简称平移。平移不改变图形的形状和大小。图形经过平移,对应线段相等,对应角相等,对应点所连的线段相等。
8 平移的特征:
图形平移前后的形状和大小没有变化,只是位置发生变化。
9 对平移和旋转现象的初步认识:
①张叔叔在笔直的公路上开车,方向盘的运动是(旋转)现象。
②升国旗时,国旗的升降运动是(平移)现象。
③妈妈用拖布擦地,是(平移)现象。
④自行车的车轮转了一圈又一圈是(旋转)现象。
10 镜子内外的左右方向是相反的。
统 计
数据的整理和表示
1、对调查数据的整理和表示:
可以通过写“正”字或者画条形图的方式。
2、信息应用:
可以通过数据统计得到哪个选项得票最多或最少,从而决定该怎样选择。还可以知道任意两个选项的得票数量差。
