八年级数学上册试题 19.9勾股定理(含解析)-沪教版
文档属性
| 名称 | 八年级数学上册试题 19.9勾股定理(含解析)-沪教版 |
|
|
| 格式 | docx | ||
| 文件大小 | 250.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-27 15:30:36 | ||
图片预览




文档简介
19.9勾股定理
一、选择题.
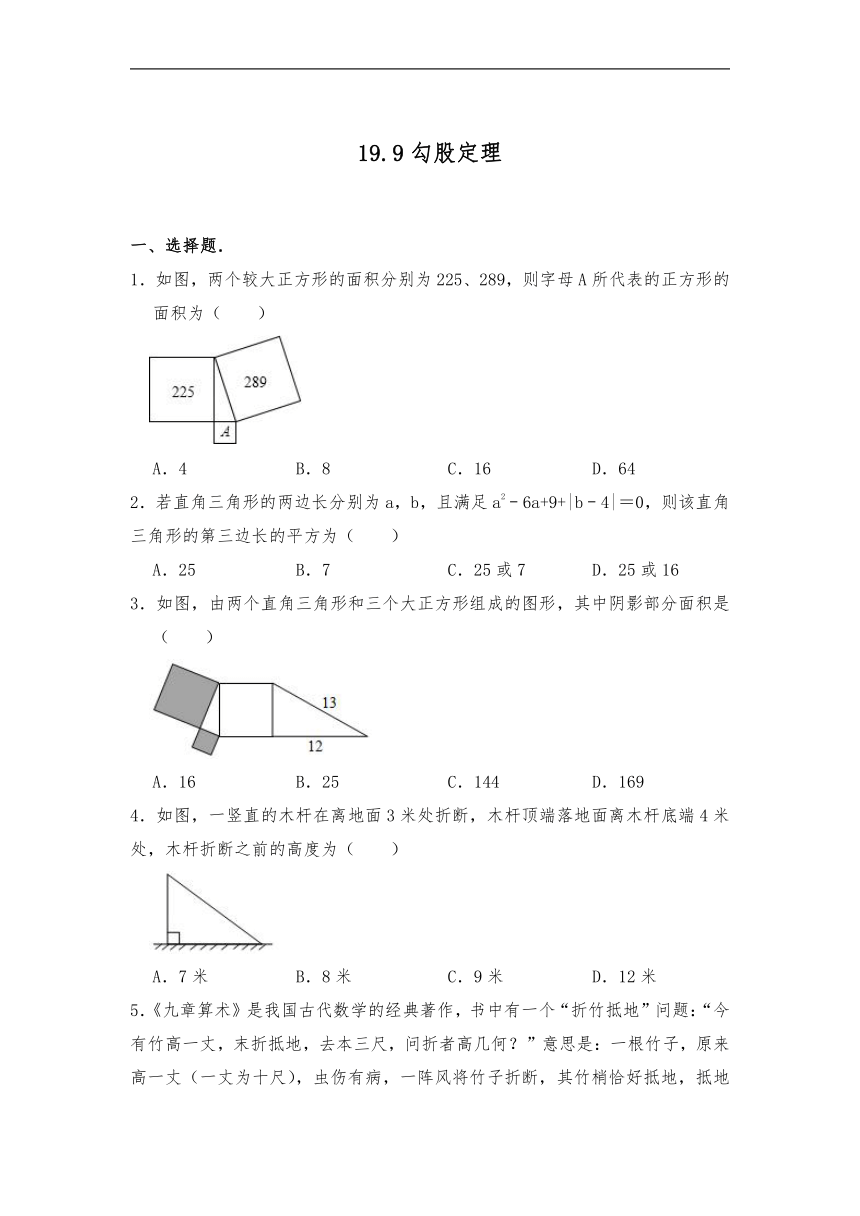
1.如图,两个较大正方形的面积分别为225、289,则字母A所代表的正方形的面积为( )
A.4 B.8 C.16 D.64
2.若直角三角形的两边长分别为a,b,且满足a2﹣6a+9+|b﹣4|=0,则该直角三角形的第三边长的平方为( )
A.25 B.7 C.25或7 D.25或16
3.如图,由两个直角三角形和三个大正方形组成的图形,其中阴影部分面积是( )
A.16 B.25 C.144 D.169
4.如图,一竖直的木杆在离地面3米处折断,木杆顶端落地面离木杆底端4米处,木杆折断之前的高度为( )
A.7米 B.8米 C.9米 D.12米
5.《九章算术》是我国古代数学的经典著作,书中有一个“折竹抵地”问题:“今有竹高一丈,末折抵地,去本三尺,问折者高几何?”意思是:一根竹子,原来高一丈(一丈为十尺),虫伤有病,一阵风将竹子折断,其竹梢恰好抵地,抵地处离原竹子根部三尺远,问:原处还有多高的竹子?( )
A.4尺 B.4.55尺 C.5尺 D.5.55尺
6.两个边长分别为a,b,c的直角三角形和一个两条直角边都是c的直角三角形拼成如图所示的图形,用两种不同的计算方法计算这个图形的面积,则可得等式为( )
A.(a+b)2=c2 B.(a﹣b)2=c2 C.a2+b2=c2 D.a2﹣b2=c2
7.如图,是由四个全等的直角三角形与中间一个小正方形拼成的个大正方形,若大正方形的面积是17,小正方形的面积是1,直角三角形的两直角边分别为a,b,则(a+b)2的值是( )
A.13 B.25 C.33 D.144
8.如图,∠ACD是△ABC的外角,CE平分∠ACB,交AB于E,CF平分∠ACD,且EF∥BC交AC、CF于M、F,若EM=3,则CE2+CF2的值为( )
A.36 B.9 C.6 D.18
9.如图,四个全等的直角三角形和中间的小正方形可以拼成一个大正方形,若直角三角形的较长直角边长为a,较短直角边长为b,大正方形面积为S1,小正方形面积为S2,则(a+b)2可以表示为( )
A.S1﹣S2 B.S1+S2 C.2S1﹣S2 D.S1+2S2
10.如图所示的是一种“羊头”形图案,全部由正方形与等腰直角三角形构成,其作法是从正方形①开始,以它的一条边为斜边,向外作等腰直角三角形,然后再以其直角边为边,分别向外作正方形②和②′,再分别以正方形②和②′的一条边为斜边,向外作等腰直角三角形,…,若正方形⑤的面积为2cm2,则正方形①的面积为( )
A.8cm2 B.16cm2 C.32cm2 D.64ccm2
二、填空题
11.已知一个直角三角形的两边长分别是a,b且a,b满足|b﹣4|=0.则斜边长是 .
12.在Rt△ABC中,∠C=90°,如果AB=15,AC=12,那么Rt△ABC的面积是 .
13.如图,已知正方形ABCD的面积为4,正方形FHIJ的面积为3,点D、C、G、J、I在同一水平面上,则正方形BEFG的面积为 .
14.《九章算术》中有一个“折竹抵地”问题:“今有竹高九尺,末折抵地,去本三尺,问折者高几何?”意思是:现有竹子高9尺,折后竹尖抵地与竹子底部的距离为3尺,问折处高几尺?即:如图,AB+AC=9尺,BC=3尺,则AC= 尺.
15.如图,每个小正方形的边长都为1,则△ABC的周长为 .
16.如图,已知在Rt△ABC中,∠ACB=90°,分别以AC,BC,AB为直径作半圆,面积分别记为S1,S2,S3,若S3=9π,则S1+S2等于 .
17.将一根24cm的筷子,置于底面直径为5cm、高为12cm的圆柱体中,如图,设筷子露出在杯子外面长为hcm,则h的最小值 ,h的最大值 .
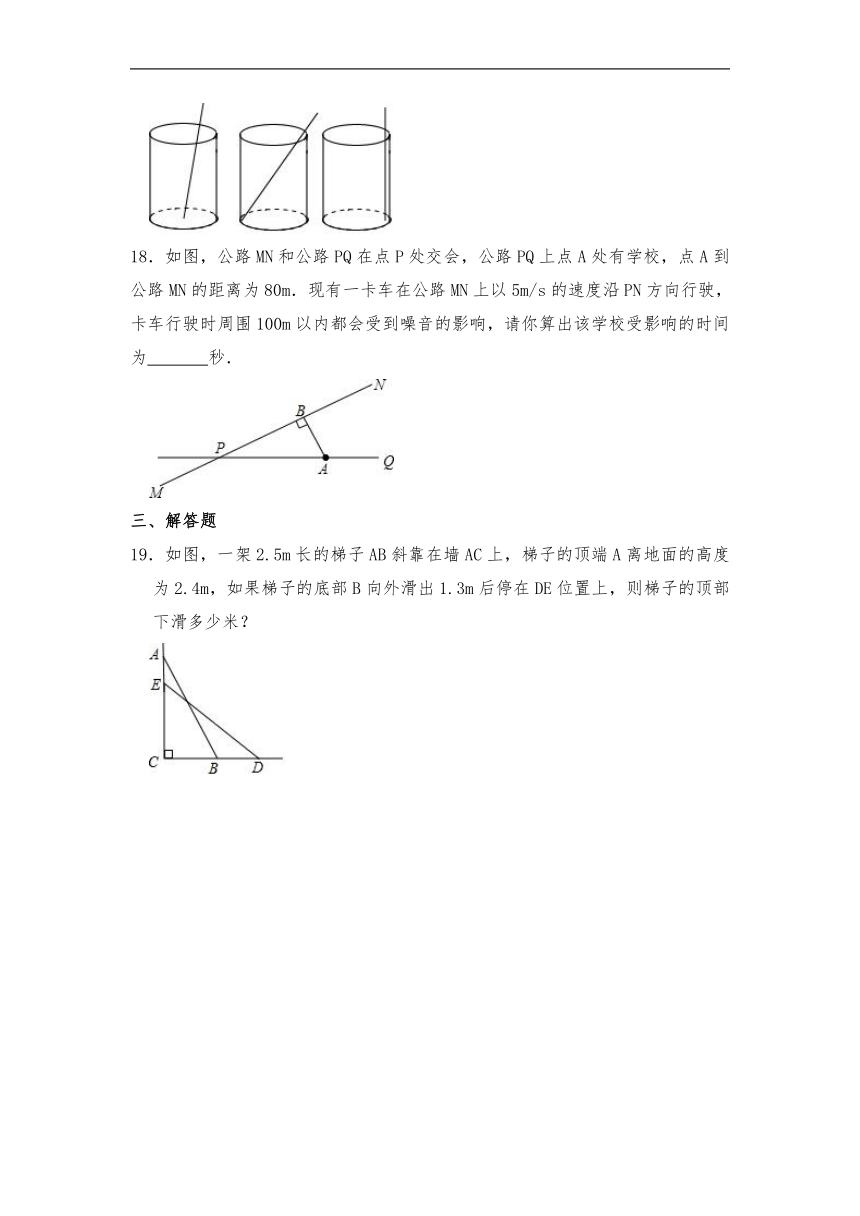
18.如图,公路MN和公路PQ在点P处交会,公路PQ上点A处有学校,点A到公路MN的距离为80m.现有一卡车在公路MN上以5m/s的速度沿PN方向行驶,卡车行驶时周围100m以内都会受到噪音的影响,请你算出该学校受影响的时间为 秒.
三、解答题
19.如图,一架2.5m长的梯子AB斜靠在墙AC上,梯子的顶端A离地面的高度为2.4m,如果梯子的底部B向外滑出1.3m后停在DE位置上,则梯子的顶部下滑多少米?
20.“交通管理条例第三十五条”规定:小汽车在城街路上行驶速度不得超过70千米/小时,如图,一辆小汽车在一条城市街路上直道行驶,某一时刻刚好行驶到路面对车速检测仪正前方50米处,过了6秒后,测得小汽车与车速检测仪间距离为130米,这辆小汽车超速了吗?
21.《九章算术》是我国古代最重要的数学著作之一,在“勾股”章中记载了一道“折竹抵地”问题:“今有竹高一丈,末折抵地,去本三尺,问折者高几何?”可翻译为:有一根竹子高一丈,今在A处折断,竹梢落在地面的B处,B与竹根部C相距3尺,求折断点A与地面的高度AC.(注:1丈=10尺)
22.如图是一底面周长为24m,高为6m的圆柱形油罐,一只老鼠欲从距地面1m的A处沿侧面爬行到对角B处吃食物,请算出老鼠爬行的最短路程为多少?
23.勾股定理神奇而美妙,它的证法多种多样,在学习了教材中介绍的拼图证法以后,小华突发灵感,给出了如图拼图:
两个全等的直角三角板ABC和直角三角板DEF,顶点F在BC边上,顶点C、D重合,连接AE、EB.设AB、DE交于点G.∠ACB=∠DFE=90°,BC=EF=a,AC=DF=b(a>b),AB=DE=c.请你回答以下问题:
(1)填空:∠AGE= °,S四边形ADBE= c2.
(2)请用两种方法计算四边形ACBE的面积,并以此为基础证明勾股定理.
24.知识探究:
如图1是两直角边长分别为m,n(m>n)的直角三角形,如果用四个与图1完全一样的直角三角形可以拼成如图2和图3的几何图形.其中图2和图3的四边形ABCD、四边形EFGH都是正方形.请你根据几何图形部分与整体的关系完成第(1)(2)题.
请选择(m+n)2,(m﹣n)2,mn中的有关代数式表示:
图2中正方形ABCD的面积: .
图3中正方形ABCD的面积: .
(2)请你根据题(1),写出下列三个代数式:(m+n)2,(m﹣n)2,mn之间的等量关系 .
知识应用:
(3)根据(2)题中的等量关系,解决如下问题:
①已知:a﹣b=5,ab=﹣6,求:(a+b)2的值;
②已知:a>0,a,求:a的值.
答案
一、选择题.
1.
【分析】根据正方形的面积等于边长的平方,由正方形PQED的面积和正方形PRQF的面积分别表示出PR的平方及PQ的平方,又三角形PQR为直角三角形,根据勾股定理求出QR的平方,即为所求正方形的面积.
【解析】∵正方形PQED的面积等于225,
∴即PQ2=225,
∵正方形PRGF的面积为289,
∴PR2=289,
又△PQR为直角三角形,根据勾股定理得:
PR2=PQ2+QR2,
∴QR2=PR2﹣PQ2=289﹣225=64,
则正方形QMNR的面积为64.
故选:D.
2.
【分析】根据非负数的性质列出方程求出a、b的值,根据勾股定理即可得到结论.
【解析】∵a2﹣6a+9+|b﹣4|=0,
∴(a﹣3)2=0,b﹣4=0,
∴a=3,b=4,
∴直角三角形的第三边长5,或直角三角形的第三边长,
∴直角三角形的第三平方为25或7,
故选:C.
3.
【分析】根据勾股定理解答即可.
【解析】
根据勾股定理得出:AB,
∴EF=AB=5,
∴阴影部分面积是25,
故选:B.
4.
【分析】由题意得,在直角三角形中,知道了两直角边,运用勾股定理即可求出斜边,从而得出这棵树折断之前的高度.
【解析】∵一竖直的木杆在离地面3米处折断,木杆顶端落地面离木杆底端4米处,
∴折断的部分长为5(米),
∴折断前高度为5+3=8(米).
故选:B.
5.
【分析】竹子折断后刚好构成一直角三角形,设竹子折断处离地面x尺,则斜边为(10﹣x)尺.利用勾股定理解题即可.
【解析】设竹子折断处离地面x尺,则斜边为(10﹣x)尺,
根据勾股定理得:x2+32=(10﹣x)2
解得:x=4.55.
答:原处还有4.55尺高的竹子.
故选:B.
6.
【分析】用两种方法求图形面积,一是直接利用梯形面积公式来求;一是利用三个三角形面积之和来求.
【解析】根据题意得:S(a+b)(a+b),Sababc2,
∴(a+b)(a+b)ababc2,即(a+b)(a+b)=ab+ab+c2,
整理得:a2+b2=c2.
故选:C.
7.
【分析】根据正方形的面积公式以及勾股定理,结合图形进行分析发现:大正方形的面积即直角三角形斜边的平方17,也就是两条直角边的平方和是17,四个直角三角形的面积和是大正方形的面积减去小正方形的面积即2ab=16.根据完全平方公式即可求解.
【解析】根据题意,结合勾股定理a2+b2=17,
四个三角形的面积=4ab=17﹣1,
∴2ab=16,
联立解得:(a+b)2=17+16=33.
故选:C.
8.
【分析】根据角平分线的定义可以证明出△CEF是直角三角形,再根据平行线的性质以及角平分线的定义证明得到EM=CM=MF然后求出EF的长度,然后利用勾股定理列式计算即可求解.
【解析】∵CE平分∠ACB交AB于E,CF平分∠ACD,
∴∠1=∠2∠ACB,∠3=∠4∠ACD,
∴∠2+∠3(∠ACB+∠ACD)=90°,
∴△CEF是直角三角形,
∵EF∥BC,
∴∠1=∠5,∠4=∠F,
∴∠2=∠5,∠3=∠F,
∴EM=CM,CM=MF,
∵EM=3,
∴EF=3+3=6,
在Rt△CEF中,CE2+CF2=EF2=62=36.
故选:A.
9.
【分析】根据图形和勾股定理可知S1=c2=a2+b2,再由完全平方公式即可得到结果.
【解析】如图所示:设直角三角形的斜边为c,
则S1=c2=a2+b2
S2=(a﹣b)2=a2+b2﹣2ab,
∴2ab=S1﹣S2,
∴(a+b)2=a2+2ab+b2=S1+S1﹣S2=2S1﹣S2,
故选:C.
10.
【分析】根据题意可知第一个正方形的面积是S,则第二个正方形的面积是,…,进而可找出规律得出第n个正方形的面积,即可得出结果.
【解析】第一个正方形的面积是S;
第二个正方形的面积是;
第三个正方形的面积是;
…
第n个正方形的面积是,
∵正方形⑤的面积是2,
∴正方形①的面积32.
故选:C.
二、填空题
11.
【分析】由绝对值和算术平方根的非负性质求出a=3,b=4,再分两种情况求解即可.
【解析】∵直角三角形的两边长分别是a,b且a,b满足|b﹣4|=0,
∴a﹣3=0,且b﹣4=0,
∴a=3,b=4,
分两种情况:
①4为直角边长时,斜边长5;
②4为斜边长时,斜边长=4;
故答案为:5或4.
12.
【分析】在Rt△ABC中,利用勾股定理可求出BC的长度,即可解决问题.
【解析】∵在Rt△ABC中,∠C=90°,AB=15,AC=12,
∴BC9.
∴S△ABC9×12=54
故答案为:54.
13.
【分析】由正方形的性质及“一线三等角“得出条件,判定△BCG≌△GJF(AAS),则BC=GJ,根据正方形ABCD的面积为4,正方形FHIJ的面积为3,以及勾股定理可得答案.
【解析】∵四边形ABCD、四边形FHIJ和四边形BEFG都是正方形,
∴∠BCG=∠BGF=∠GJF=90°,BG=GF,
∴∠CBG+∠BGC=90°,∠JGF+∠BGC=90°,
∴∠CBG=∠JGF,
在△BCG和△GJF中,
,
∴△BCG≌△GJF(AAS),
∴BC=GJ,
∵正方形ABCD的面积为4,正方形FHIJ的面积为3,
∴BC2=4,FJ2=3,
∴GJ2=4,
在Rt△GJF中,由勾股定理得:
FG2=GJ2+FJ2=4+3=7,
∴正方形BEFG的面积为7.
故答案为:7.
14.
【分析】竹子折断后刚好构成一直角三角形,设竹子折断处离地面x尺,则斜边为(9﹣x)尺,利用勾股定理解题即可.
【解析】设竹子折断处离地面x尺,则斜边为(9﹣x)尺,
根据勾股定理得:x2+32=(9﹣x)2.
解得:x=4,
答:折断处离地面的高度为4尺.
故答案为:4.
15.
【分析】根据题意和勾股定理,可以求得AB、BC、AC的长,然后即可得到△ABC的周长.
【解析】由题意可得,
AB,BC,AC2,
∴△ABC的周长为:2,
故答案为:2.
16.
【分析】根据勾股定理和圆的面积公式,可以得到S1+S2的值,从而可以解答本题.
【解析】∵∠ACB=90°,
∴AC2+BC2=AB2,
∵S1=π()2,S2=π()2,S3=π()2,
∴S1+S2=π()2π()2π()2S3,
∵S3=9π,
∴S1+S2=9π,
故答案为:9π.
17.
【分析】当筷子与杯底垂直时h最大,当筷子与杯底及杯高构成直角三角形时h最小,据此可以得到h的取值范围.
【解析】当筷子与杯底垂直时h最大,h最大=24﹣12=12(cm).
当筷子与杯底及杯高构成直角三角形时h最小,
此时,在杯子内部分13(cm),
故h=24﹣13=11(cm).
故h的取值范围是11≤h≤12.
故答案为:11cm;12cm.
18.
【分析】设卡车开到C处刚好开始受到影响,行驶到D处时结束,在Rt△ACB中求出CB,继而得出CD,再由卡车的速度可得出所需时间.
【解析】设卡车开到C处刚好开始受到影响,行驶到D处时结束了噪声的影响.
则有CA=DA=100m,
在Rt△ABC中,CB60(m),
∴CD=2CB=120(m),
则该校受影响的时间为:120÷5=24(s).
答:该学校受影响的时间为24秒,
故答案为:24.
三、解答题
19.由题意得,AB=DE=2.5,AC=2.4,BD=1.3,
∵∠C=90°,
∴BC0.7,
∴CD=BC+BD=2,
∵CE1.5,
∴AE=AC﹣CE=2.4﹣1.5=0.9,
答:梯子的顶部下滑0.9米.
20.
【分析】利用勾股定理列式求出BC,再根据速度=路程÷时间求出小汽车的速度,然后化为千米/小时的单位即可得解.
【解析】由勾股定理得,BC120米,
v=120÷6=20米/秒,
∵20×3.6=72,
∴20米/秒=72千米/小时,72>70,
∴这辆小汽车超速了.
21.设AC=x,
∵AC+AB=10,
∴AB=10﹣x.
∵在Rt△ABC中,∠ACB=90°,
∴AC2+BC2=AB2,即x2+32=(10﹣x)2.
解得:x=4.55,
即AC=4.55.
22.
【解析】
延AC和BD剪开,将曲面平铺在平面上,过AE作AE⊥BD于E,如图,
∵底面周长为24m,高为6m的圆柱形油罐,
∴AE=12m,BE=6﹣1=5(m),
在Rt△AEB中,由勾股定理得:AB13(m),
∴老鼠爬行的最短路程为13m.
23.(1)∵△ABC≌△DEF,
∴∠EDF=∠CAB,
∵∠EDF+∠CAE=90°,
∴∠ACE+∠CAB=90°,
∴∠AGC=90°,
∴∠AGE=180°﹣∠AGC=90°;
∴DE⊥AB,
∴S四边形ADBE=S△ACB+S△ABEAB DGAB EGAB (DG+EG)AB DEc2,
故答案为:90,;
(2)∵四边形ACBE的面积=S△ACB+S△ABEAB DGAB EGAB (DG+EG)AB DEc2,
四边形ACBE的面积=S四边形ACFE+S△EFB(AC+EF) CFBF EF(b+a)b(a﹣b) ab2aba2aba2b2,
∴c2a2b2,
即a2+b2=c2.
24.(1)图2中,正方形ABCD面积为AB2,
由图1得AB2=m2+n2,
∴由图中正方形EFGH面积加上四个直角三角形面积等于正方形ABCD的面积可得:
m2+n2=(m﹣n)2+2mn;
图3中正方形ABCD的面积为AB2=m2+n2=(m+n)2﹣2mn.
故答案为:(m﹣n)2+2mn;(m+n)2﹣2mn.
(2)∵图2中正方形EFGH的面积为(m﹣n)2,
而S△ABG=S△DAF=S△CDE=S△BCH.
∴图2中正方形ABCD的面积=(m﹣n)2+4(m﹣n)2+2mn.
又∵图3中正方形ABCD的面积=(m+n)2﹣2mn,
图2与图3中正方形ABCD的边长都是图1中直角三角形的斜边,
∴图1中正方形ABCD的面积=图2中正方形ABCD的面积.
故(m﹣n)2+2mn=(m+n)2﹣2mn.
∴(m﹣n)2=(m+n)2﹣4mn或者(m+n)2=(m﹣n)2+4mn.
故答案为:(m﹣n)2=(m+n)2﹣4mn或者(m+n)2=(m﹣n)2+4mn.
(3)由(1)可得:
(a+b)2=(a﹣b)2+4ab=52+4×(﹣6)=25﹣24=1;
,
∴,
又a>0,
∴.
一、选择题.
1.如图,两个较大正方形的面积分别为225、289,则字母A所代表的正方形的面积为( )
A.4 B.8 C.16 D.64
2.若直角三角形的两边长分别为a,b,且满足a2﹣6a+9+|b﹣4|=0,则该直角三角形的第三边长的平方为( )
A.25 B.7 C.25或7 D.25或16
3.如图,由两个直角三角形和三个大正方形组成的图形,其中阴影部分面积是( )
A.16 B.25 C.144 D.169
4.如图,一竖直的木杆在离地面3米处折断,木杆顶端落地面离木杆底端4米处,木杆折断之前的高度为( )
A.7米 B.8米 C.9米 D.12米
5.《九章算术》是我国古代数学的经典著作,书中有一个“折竹抵地”问题:“今有竹高一丈,末折抵地,去本三尺,问折者高几何?”意思是:一根竹子,原来高一丈(一丈为十尺),虫伤有病,一阵风将竹子折断,其竹梢恰好抵地,抵地处离原竹子根部三尺远,问:原处还有多高的竹子?( )
A.4尺 B.4.55尺 C.5尺 D.5.55尺
6.两个边长分别为a,b,c的直角三角形和一个两条直角边都是c的直角三角形拼成如图所示的图形,用两种不同的计算方法计算这个图形的面积,则可得等式为( )
A.(a+b)2=c2 B.(a﹣b)2=c2 C.a2+b2=c2 D.a2﹣b2=c2
7.如图,是由四个全等的直角三角形与中间一个小正方形拼成的个大正方形,若大正方形的面积是17,小正方形的面积是1,直角三角形的两直角边分别为a,b,则(a+b)2的值是( )
A.13 B.25 C.33 D.144
8.如图,∠ACD是△ABC的外角,CE平分∠ACB,交AB于E,CF平分∠ACD,且EF∥BC交AC、CF于M、F,若EM=3,则CE2+CF2的值为( )
A.36 B.9 C.6 D.18
9.如图,四个全等的直角三角形和中间的小正方形可以拼成一个大正方形,若直角三角形的较长直角边长为a,较短直角边长为b,大正方形面积为S1,小正方形面积为S2,则(a+b)2可以表示为( )
A.S1﹣S2 B.S1+S2 C.2S1﹣S2 D.S1+2S2
10.如图所示的是一种“羊头”形图案,全部由正方形与等腰直角三角形构成,其作法是从正方形①开始,以它的一条边为斜边,向外作等腰直角三角形,然后再以其直角边为边,分别向外作正方形②和②′,再分别以正方形②和②′的一条边为斜边,向外作等腰直角三角形,…,若正方形⑤的面积为2cm2,则正方形①的面积为( )
A.8cm2 B.16cm2 C.32cm2 D.64ccm2
二、填空题
11.已知一个直角三角形的两边长分别是a,b且a,b满足|b﹣4|=0.则斜边长是 .
12.在Rt△ABC中,∠C=90°,如果AB=15,AC=12,那么Rt△ABC的面积是 .
13.如图,已知正方形ABCD的面积为4,正方形FHIJ的面积为3,点D、C、G、J、I在同一水平面上,则正方形BEFG的面积为 .
14.《九章算术》中有一个“折竹抵地”问题:“今有竹高九尺,末折抵地,去本三尺,问折者高几何?”意思是:现有竹子高9尺,折后竹尖抵地与竹子底部的距离为3尺,问折处高几尺?即:如图,AB+AC=9尺,BC=3尺,则AC= 尺.
15.如图,每个小正方形的边长都为1,则△ABC的周长为 .
16.如图,已知在Rt△ABC中,∠ACB=90°,分别以AC,BC,AB为直径作半圆,面积分别记为S1,S2,S3,若S3=9π,则S1+S2等于 .
17.将一根24cm的筷子,置于底面直径为5cm、高为12cm的圆柱体中,如图,设筷子露出在杯子外面长为hcm,则h的最小值 ,h的最大值 .
18.如图,公路MN和公路PQ在点P处交会,公路PQ上点A处有学校,点A到公路MN的距离为80m.现有一卡车在公路MN上以5m/s的速度沿PN方向行驶,卡车行驶时周围100m以内都会受到噪音的影响,请你算出该学校受影响的时间为 秒.
三、解答题
19.如图,一架2.5m长的梯子AB斜靠在墙AC上,梯子的顶端A离地面的高度为2.4m,如果梯子的底部B向外滑出1.3m后停在DE位置上,则梯子的顶部下滑多少米?
20.“交通管理条例第三十五条”规定:小汽车在城街路上行驶速度不得超过70千米/小时,如图,一辆小汽车在一条城市街路上直道行驶,某一时刻刚好行驶到路面对车速检测仪正前方50米处,过了6秒后,测得小汽车与车速检测仪间距离为130米,这辆小汽车超速了吗?
21.《九章算术》是我国古代最重要的数学著作之一,在“勾股”章中记载了一道“折竹抵地”问题:“今有竹高一丈,末折抵地,去本三尺,问折者高几何?”可翻译为:有一根竹子高一丈,今在A处折断,竹梢落在地面的B处,B与竹根部C相距3尺,求折断点A与地面的高度AC.(注:1丈=10尺)
22.如图是一底面周长为24m,高为6m的圆柱形油罐,一只老鼠欲从距地面1m的A处沿侧面爬行到对角B处吃食物,请算出老鼠爬行的最短路程为多少?
23.勾股定理神奇而美妙,它的证法多种多样,在学习了教材中介绍的拼图证法以后,小华突发灵感,给出了如图拼图:
两个全等的直角三角板ABC和直角三角板DEF,顶点F在BC边上,顶点C、D重合,连接AE、EB.设AB、DE交于点G.∠ACB=∠DFE=90°,BC=EF=a,AC=DF=b(a>b),AB=DE=c.请你回答以下问题:
(1)填空:∠AGE= °,S四边形ADBE= c2.
(2)请用两种方法计算四边形ACBE的面积,并以此为基础证明勾股定理.
24.知识探究:
如图1是两直角边长分别为m,n(m>n)的直角三角形,如果用四个与图1完全一样的直角三角形可以拼成如图2和图3的几何图形.其中图2和图3的四边形ABCD、四边形EFGH都是正方形.请你根据几何图形部分与整体的关系完成第(1)(2)题.
请选择(m+n)2,(m﹣n)2,mn中的有关代数式表示:
图2中正方形ABCD的面积: .
图3中正方形ABCD的面积: .
(2)请你根据题(1),写出下列三个代数式:(m+n)2,(m﹣n)2,mn之间的等量关系 .
知识应用:
(3)根据(2)题中的等量关系,解决如下问题:
①已知:a﹣b=5,ab=﹣6,求:(a+b)2的值;
②已知:a>0,a,求:a的值.
答案
一、选择题.
1.
【分析】根据正方形的面积等于边长的平方,由正方形PQED的面积和正方形PRQF的面积分别表示出PR的平方及PQ的平方,又三角形PQR为直角三角形,根据勾股定理求出QR的平方,即为所求正方形的面积.
【解析】∵正方形PQED的面积等于225,
∴即PQ2=225,
∵正方形PRGF的面积为289,
∴PR2=289,
又△PQR为直角三角形,根据勾股定理得:
PR2=PQ2+QR2,
∴QR2=PR2﹣PQ2=289﹣225=64,
则正方形QMNR的面积为64.
故选:D.
2.
【分析】根据非负数的性质列出方程求出a、b的值,根据勾股定理即可得到结论.
【解析】∵a2﹣6a+9+|b﹣4|=0,
∴(a﹣3)2=0,b﹣4=0,
∴a=3,b=4,
∴直角三角形的第三边长5,或直角三角形的第三边长,
∴直角三角形的第三平方为25或7,
故选:C.
3.
【分析】根据勾股定理解答即可.
【解析】
根据勾股定理得出:AB,
∴EF=AB=5,
∴阴影部分面积是25,
故选:B.
4.
【分析】由题意得,在直角三角形中,知道了两直角边,运用勾股定理即可求出斜边,从而得出这棵树折断之前的高度.
【解析】∵一竖直的木杆在离地面3米处折断,木杆顶端落地面离木杆底端4米处,
∴折断的部分长为5(米),
∴折断前高度为5+3=8(米).
故选:B.
5.
【分析】竹子折断后刚好构成一直角三角形,设竹子折断处离地面x尺,则斜边为(10﹣x)尺.利用勾股定理解题即可.
【解析】设竹子折断处离地面x尺,则斜边为(10﹣x)尺,
根据勾股定理得:x2+32=(10﹣x)2
解得:x=4.55.
答:原处还有4.55尺高的竹子.
故选:B.
6.
【分析】用两种方法求图形面积,一是直接利用梯形面积公式来求;一是利用三个三角形面积之和来求.
【解析】根据题意得:S(a+b)(a+b),Sababc2,
∴(a+b)(a+b)ababc2,即(a+b)(a+b)=ab+ab+c2,
整理得:a2+b2=c2.
故选:C.
7.
【分析】根据正方形的面积公式以及勾股定理,结合图形进行分析发现:大正方形的面积即直角三角形斜边的平方17,也就是两条直角边的平方和是17,四个直角三角形的面积和是大正方形的面积减去小正方形的面积即2ab=16.根据完全平方公式即可求解.
【解析】根据题意,结合勾股定理a2+b2=17,
四个三角形的面积=4ab=17﹣1,
∴2ab=16,
联立解得:(a+b)2=17+16=33.
故选:C.
8.
【分析】根据角平分线的定义可以证明出△CEF是直角三角形,再根据平行线的性质以及角平分线的定义证明得到EM=CM=MF然后求出EF的长度,然后利用勾股定理列式计算即可求解.
【解析】∵CE平分∠ACB交AB于E,CF平分∠ACD,
∴∠1=∠2∠ACB,∠3=∠4∠ACD,
∴∠2+∠3(∠ACB+∠ACD)=90°,
∴△CEF是直角三角形,
∵EF∥BC,
∴∠1=∠5,∠4=∠F,
∴∠2=∠5,∠3=∠F,
∴EM=CM,CM=MF,
∵EM=3,
∴EF=3+3=6,
在Rt△CEF中,CE2+CF2=EF2=62=36.
故选:A.
9.
【分析】根据图形和勾股定理可知S1=c2=a2+b2,再由完全平方公式即可得到结果.
【解析】如图所示:设直角三角形的斜边为c,
则S1=c2=a2+b2
S2=(a﹣b)2=a2+b2﹣2ab,
∴2ab=S1﹣S2,
∴(a+b)2=a2+2ab+b2=S1+S1﹣S2=2S1﹣S2,
故选:C.
10.
【分析】根据题意可知第一个正方形的面积是S,则第二个正方形的面积是,…,进而可找出规律得出第n个正方形的面积,即可得出结果.
【解析】第一个正方形的面积是S;
第二个正方形的面积是;
第三个正方形的面积是;
…
第n个正方形的面积是,
∵正方形⑤的面积是2,
∴正方形①的面积32.
故选:C.
二、填空题
11.
【分析】由绝对值和算术平方根的非负性质求出a=3,b=4,再分两种情况求解即可.
【解析】∵直角三角形的两边长分别是a,b且a,b满足|b﹣4|=0,
∴a﹣3=0,且b﹣4=0,
∴a=3,b=4,
分两种情况:
①4为直角边长时,斜边长5;
②4为斜边长时,斜边长=4;
故答案为:5或4.
12.
【分析】在Rt△ABC中,利用勾股定理可求出BC的长度,即可解决问题.
【解析】∵在Rt△ABC中,∠C=90°,AB=15,AC=12,
∴BC9.
∴S△ABC9×12=54
故答案为:54.
13.
【分析】由正方形的性质及“一线三等角“得出条件,判定△BCG≌△GJF(AAS),则BC=GJ,根据正方形ABCD的面积为4,正方形FHIJ的面积为3,以及勾股定理可得答案.
【解析】∵四边形ABCD、四边形FHIJ和四边形BEFG都是正方形,
∴∠BCG=∠BGF=∠GJF=90°,BG=GF,
∴∠CBG+∠BGC=90°,∠JGF+∠BGC=90°,
∴∠CBG=∠JGF,
在△BCG和△GJF中,
,
∴△BCG≌△GJF(AAS),
∴BC=GJ,
∵正方形ABCD的面积为4,正方形FHIJ的面积为3,
∴BC2=4,FJ2=3,
∴GJ2=4,
在Rt△GJF中,由勾股定理得:
FG2=GJ2+FJ2=4+3=7,
∴正方形BEFG的面积为7.
故答案为:7.
14.
【分析】竹子折断后刚好构成一直角三角形,设竹子折断处离地面x尺,则斜边为(9﹣x)尺,利用勾股定理解题即可.
【解析】设竹子折断处离地面x尺,则斜边为(9﹣x)尺,
根据勾股定理得:x2+32=(9﹣x)2.
解得:x=4,
答:折断处离地面的高度为4尺.
故答案为:4.
15.
【分析】根据题意和勾股定理,可以求得AB、BC、AC的长,然后即可得到△ABC的周长.
【解析】由题意可得,
AB,BC,AC2,
∴△ABC的周长为:2,
故答案为:2.
16.
【分析】根据勾股定理和圆的面积公式,可以得到S1+S2的值,从而可以解答本题.
【解析】∵∠ACB=90°,
∴AC2+BC2=AB2,
∵S1=π()2,S2=π()2,S3=π()2,
∴S1+S2=π()2π()2π()2S3,
∵S3=9π,
∴S1+S2=9π,
故答案为:9π.
17.
【分析】当筷子与杯底垂直时h最大,当筷子与杯底及杯高构成直角三角形时h最小,据此可以得到h的取值范围.
【解析】当筷子与杯底垂直时h最大,h最大=24﹣12=12(cm).
当筷子与杯底及杯高构成直角三角形时h最小,
此时,在杯子内部分13(cm),
故h=24﹣13=11(cm).
故h的取值范围是11≤h≤12.
故答案为:11cm;12cm.
18.
【分析】设卡车开到C处刚好开始受到影响,行驶到D处时结束,在Rt△ACB中求出CB,继而得出CD,再由卡车的速度可得出所需时间.
【解析】设卡车开到C处刚好开始受到影响,行驶到D处时结束了噪声的影响.
则有CA=DA=100m,
在Rt△ABC中,CB60(m),
∴CD=2CB=120(m),
则该校受影响的时间为:120÷5=24(s).
答:该学校受影响的时间为24秒,
故答案为:24.
三、解答题
19.由题意得,AB=DE=2.5,AC=2.4,BD=1.3,
∵∠C=90°,
∴BC0.7,
∴CD=BC+BD=2,
∵CE1.5,
∴AE=AC﹣CE=2.4﹣1.5=0.9,
答:梯子的顶部下滑0.9米.
20.
【分析】利用勾股定理列式求出BC,再根据速度=路程÷时间求出小汽车的速度,然后化为千米/小时的单位即可得解.
【解析】由勾股定理得,BC120米,
v=120÷6=20米/秒,
∵20×3.6=72,
∴20米/秒=72千米/小时,72>70,
∴这辆小汽车超速了.
21.设AC=x,
∵AC+AB=10,
∴AB=10﹣x.
∵在Rt△ABC中,∠ACB=90°,
∴AC2+BC2=AB2,即x2+32=(10﹣x)2.
解得:x=4.55,
即AC=4.55.
22.
【解析】
延AC和BD剪开,将曲面平铺在平面上,过AE作AE⊥BD于E,如图,
∵底面周长为24m,高为6m的圆柱形油罐,
∴AE=12m,BE=6﹣1=5(m),
在Rt△AEB中,由勾股定理得:AB13(m),
∴老鼠爬行的最短路程为13m.
23.(1)∵△ABC≌△DEF,
∴∠EDF=∠CAB,
∵∠EDF+∠CAE=90°,
∴∠ACE+∠CAB=90°,
∴∠AGC=90°,
∴∠AGE=180°﹣∠AGC=90°;
∴DE⊥AB,
∴S四边形ADBE=S△ACB+S△ABEAB DGAB EGAB (DG+EG)AB DEc2,
故答案为:90,;
(2)∵四边形ACBE的面积=S△ACB+S△ABEAB DGAB EGAB (DG+EG)AB DEc2,
四边形ACBE的面积=S四边形ACFE+S△EFB(AC+EF) CFBF EF(b+a)b(a﹣b) ab2aba2aba2b2,
∴c2a2b2,
即a2+b2=c2.
24.(1)图2中,正方形ABCD面积为AB2,
由图1得AB2=m2+n2,
∴由图中正方形EFGH面积加上四个直角三角形面积等于正方形ABCD的面积可得:
m2+n2=(m﹣n)2+2mn;
图3中正方形ABCD的面积为AB2=m2+n2=(m+n)2﹣2mn.
故答案为:(m﹣n)2+2mn;(m+n)2﹣2mn.
(2)∵图2中正方形EFGH的面积为(m﹣n)2,
而S△ABG=S△DAF=S△CDE=S△BCH.
∴图2中正方形ABCD的面积=(m﹣n)2+4(m﹣n)2+2mn.
又∵图3中正方形ABCD的面积=(m+n)2﹣2mn,
图2与图3中正方形ABCD的边长都是图1中直角三角形的斜边,
∴图1中正方形ABCD的面积=图2中正方形ABCD的面积.
故(m﹣n)2+2mn=(m+n)2﹣2mn.
∴(m﹣n)2=(m+n)2﹣4mn或者(m+n)2=(m﹣n)2+4mn.
故答案为:(m﹣n)2=(m+n)2﹣4mn或者(m+n)2=(m﹣n)2+4mn.
(3)由(1)可得:
(a+b)2=(a﹣b)2+4ab=52+4×(﹣6)=25﹣24=1;
,
∴,
又a>0,
∴.
