数学:22.4 圆周角 同步试题(北京课改版九年级上)
文档属性
| 名称 | 数学:22.4 圆周角 同步试题(北京课改版九年级上) |

|
|
| 格式 | rar | ||
| 文件大小 | 146.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 京教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-08-11 00:00:00 | ||
图片预览



文档简介
本资料来自于资源最齐全的21世纪教育网www.21cnjy.com
圆心角和圆周角
第1题. 如图,在⊙O中,弦BC//半径OA,AC与OB相交于M,∠C=20°,则∠AMB的度数为( )
A.30° B.60° C.50° D.40°
答案:B.
第2题. 在⊙O中,弦AB把⊙O分为度数比为的两条弧,则所对的圆心角的度数为( )
A.30° B.45° C.60° D.90°
答案:C.
第3题. 如图,弦AC、BD相交于点E,
∠AED=80°,∠ACD的度数为( )
A.30° B.25° C.20° D.15°
答案:A.
第4题. 如图,在⊙O中,弦EF∥直径AB,若弧AE的度数为,则弧BF的度数为 ,弧EF的度数为 ,∠EOF= ,∠EFO= .
答案:,,,.
第5题. 如图,在⊙O的内接四边形ABCD中,∠BCD=130°,则∠BOD的度数是__________.
答案:.
第6题. 一条弧所对的圆周角为80°,它所对的圆心角是____度,它所含的圆周角是____度.
答案:160,100.
第7题. 如图,在⊙O中,AB是直径,弦CD//AB,的度数为20°,则圆周角∠CPD的度数为_________.
答案:70°.
第8题. 在同圆或等圆中,如果两个圆心角、两条弧、 或
中有一组是相等,那么,所对应的其余各组量都分别相等.
答案:两条弦,两条弦的弦心距.
第9题. 已知AC.BC是⊙O的两条弦,且AC⊥BC,AC=12cm,BC=6cm,则⊙O的直径是_________,弦BC的弦心距是_________.
答案:6cm,6cm.
第10题. 同弧所对的圆心角的度数是它所对圆周角度数的_____倍.
答案:2.
第11题. AB为⊙O的直径,C、D为半圆AB上两点,且弧AC、弧CD、弧DB的度数的比为3∶2∶5,则∠AOC=_____°,∠COD=_____°,∠DOB=_____°.
答案:,,.
第12题. 一条弧所含的圆周角为80°,它所对的圆周角是___度,它所对的圆心角是___度.
答案:100,200.
第13题. 如果一个三角形的一条中线具有以下特点时:_________________,这个三角形就是直角三角形.
答案:一边的中线等于这条边的一半.
第14题. 如图,在△ABC中,以BC为直径的⊙O交AB于D,交AC于E,BD=CE.
求证:AB=AC
答案:作BD、CE的弦心距证明.
第15题. 请你根据所学的知识提出猜想,四边形ABCD满足什么条件时存在外接圆 .
答案:此题为开放题目,以下条件之一均可
(1) ∠BAD+∠BCD=180° (2) ∠ABC+∠ADC=180°
(3) ∠CAD=∠CBD (4) ∠BAC=∠BDC
(5) ∠ACB=∠ADB (6) ∠ACD=∠ABD
第16题. 如图,在△ABC中,∠A=15°,∠B=30°,AB=10,试求
△ABC外接圆的半径.
答案:∠C =135°,优弧度数为270°,,劣弧的度数为90°,AB所对的圆心角为90°,所以半径=.
第17题. AB=AC=AD,试证明:∠BAC=2∠BDC.
答案:以A为圆心,以AB为半径作圆,C、D均在⊙A上,所以,∠BAC=2∠BDC.
第18题. 下图所示的角中,圆周角是( )
答案:D.
第19题. 若一个圆内接四边形ABCD中,∠A:∠B:∠C=1:2:3,则( )
A.∠A=∠C B.∠B=2∠C C.∠B=∠D D.∠A=2∠C
答案:C.
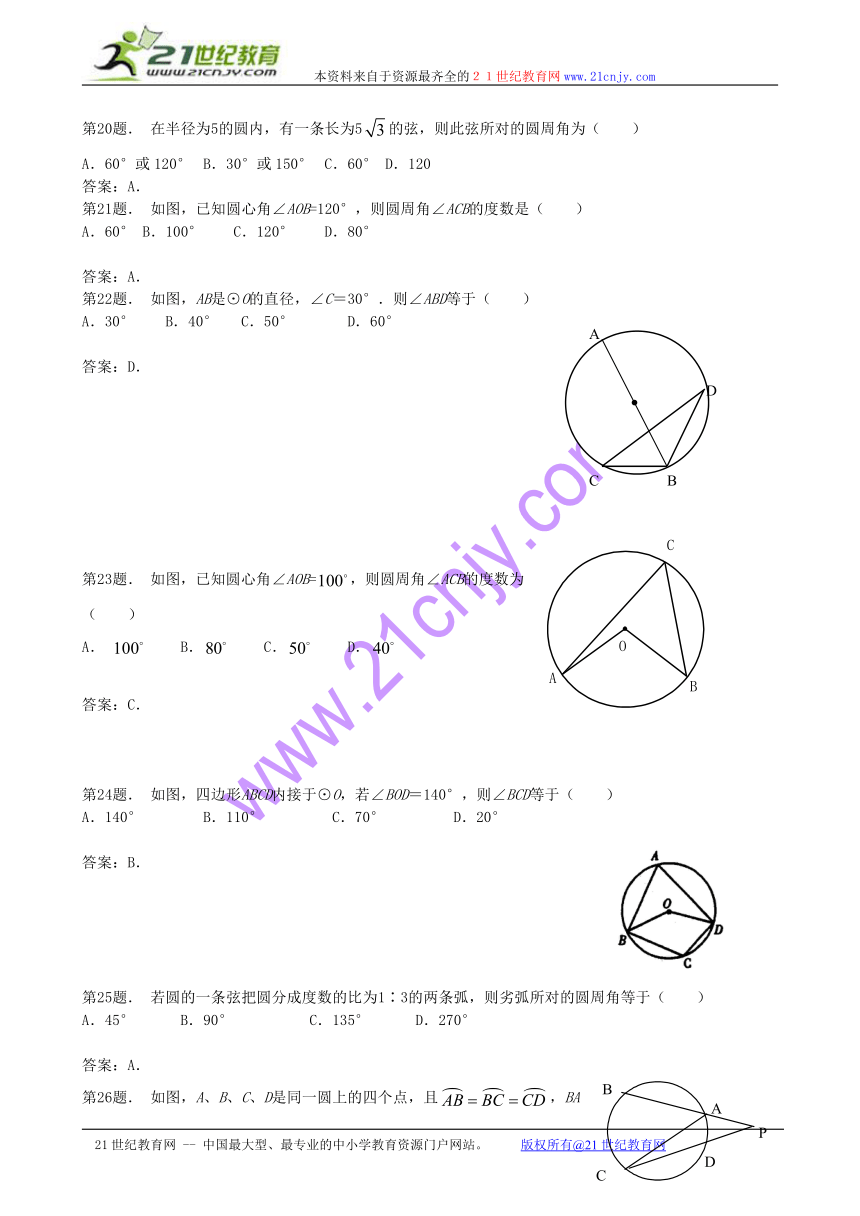
第20题. 在半径为5的圆内,有一条长为5的弦,则此弦所对的圆周角为( )
A.60°或120° B.30°或150° C.60° D.120
答案:A.
第21题. 如图,已知圆心角∠AOB=120°,则圆周角∠ACB的度数是( )
A.60° B.100° C.120° D.80°
答案:A.
第22题. 如图,AB是⊙O的直径,∠C=30°.则∠ABD等于( )
A.30° B.40° C.50° D.60°
答案:D.
第23题. 如图,已知圆心角∠AOB=,则圆周角∠ACB的度数为( )
A. B. C. D.
答案:C.
第24题. 如图,四边形ABCD内接于⊙O,若∠BOD=140°,则∠BCD等于( )
A.140° B.110° C.70° D.20°
答案:B.
第25题. 若圆的一条弦把圆分成度数的比为1∶3的两条弧,则劣弧所对的圆周角等于( )
A.45° B.90° C.135° D.270°
答案:A.
第26题. 如图,A、B、C、D是同一圆上的四个点,且,BA和CD的延长线交于P点,∠P=40°,则∠ACD的度数是( )
A.15° B.20° C.40° D.50°
答案:A.
第27题. 如图,在⊙O中,弦BC//半径OA,AC与OB相交于M,∠C=20°,则∠AMB的度数为( )
A.30° B.60° C.50° D.40°
答案:B.
第28题. 如图,A、B、C、D、E都是⊙O上的点,AB=BC=CD,∠BCD=130°
求∠AED的度数.
答案:AB=BC=CD,故,∠BCD=130°,故的度数为260°,与的度数和为100°,可得的度数为150°,所以,∠AED=75°.
第29题. 如图,在⊙O的内接四边形ABCD中,∠BCD=130°,则∠BOD的度数是__________.
答案:.
第30题. 一条弧所对的圆周角为80°,它所对的圆心角是____度,它所含的圆周角是____度.
答案:,
第31题. 已知AC、BC是⊙O的两条弦,且AC⊥BC,AC=12cm,BC=6cm,则⊙O的直径是_________,弦BC的弦心距是_________.
答案:6cm,6cm.
第32题. 一条弧所含的圆周角为80°,它所对的圆周角是___度,它所对的圆心角是___度.
答案:100,200.
第33题. 一条弧分圆为5∶7两部分,则这两条弦所对的圆周角的度数为________.
答案:75°或105°.
第34题. 如果一个三角形的一条中线具有以下特点时:_________________,这个三角形就是直角三角形.
答案:一边的中线等于这条边的一半.
第35题. 如图,四边形ABCD内接于⊙O,∠BOD=160°,则∠BAD的度数是_______,∠BCD的度数是_______.
答案:.
第36题. 如图,的度数为,那么圆周角∠ACB=_______.
答案:.
第37题. 如图AB.CD是⊙O的两条弦,则图中共有_______个圆周角.
答案:12.
第38题. 如图,在⊙O中,AB⊥CD,OE⊥BC与E,试证明:AD=2OE.
答案:A点的直径AM,连结DM、BM,AB⊥BM,作OF⊥DM于F,便可得CD//BM,所以,,于是BC=DM,OE=OF,OF是△ABC的中位线,AD=2OF,所以,AD=2OE.
第39题. 如图,四边形ABCD内接于⊙O,若∠BCD=100°,则∠BOD等于( )
A.100° B.160° C.80° D.120°
答案:B.
第40题. 如图,在⊙O中,OA=AB=BC,且OB⊥BC,则弧BD和弧DE的度数分别是 ( )
A.15°、15° B.15°、30°
C.30°、15° D.22°30′、22°30′
答案:C.
第41题. 已知:四边形ABCD的四个顶点在同一个圆上,对角线AC⊥BD,AB>CD.若CD=4,则AB与圆的距离为 ( )
A. B.2 C. D.
答案:B.
第42题. ⊙O中,AB是弦,∠OAB=50°,则弦AB所对的圆心角的度数是_________,弦AB所对的弧的度数为_________.
答案:80°,80°或280°.
第43题. 长为3的弦所对的圆周角为135°,则此圆的直径为_________.
答案:.
第44题. ⊙O的半径是5,两条弦AB=CD=8,并且AB⊥CD,垂足为P,则OP的长为___________.
答案:.
第45题. 已知:如图,EF为⊙O的直径,过EF上一点P作弦AB、CD,且∠APF=∠CPF.
求证:PA=PC.
答案:作AB、CD的弦心距OM、ON,进一步证明△OMP≌△ONP(ASA),
得到PM=PN(②);①+②即能证明结论.
第46题. 在⊙O中,OC是半径,弦EF过OC的中点,且垂直于OC,则弦EF所对的圆心角的度数是_________,如果半径为1,弦EF的长是_________.
答案:,.
第47题. 如图,弦AC、BD交于E点,且,∠BEC=130°,那么∠ACD=_________.
答案:105°.
第48题. 如图,如果⊙O的半径为2,弦AB=,那么弦心距OE的长为( )
A. B. C. D.
答案:C.
C
B
D
O
A
O
C
B
D
A
E
C
D
B
A
B
C
A
C
B
D
A
A
B
C
D
C
B
D
O
A
O
A
B
D
C
O
A
C
B
D
E
A
B
C
D
A
O
B
E
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
圆心角和圆周角
第1题. 如图,在⊙O中,弦BC//半径OA,AC与OB相交于M,∠C=20°,则∠AMB的度数为( )
A.30° B.60° C.50° D.40°
答案:B.
第2题. 在⊙O中,弦AB把⊙O分为度数比为的两条弧,则所对的圆心角的度数为( )
A.30° B.45° C.60° D.90°
答案:C.
第3题. 如图,弦AC、BD相交于点E,
∠AED=80°,∠ACD的度数为( )
A.30° B.25° C.20° D.15°
答案:A.
第4题. 如图,在⊙O中,弦EF∥直径AB,若弧AE的度数为,则弧BF的度数为 ,弧EF的度数为 ,∠EOF= ,∠EFO= .
答案:,,,.
第5题. 如图,在⊙O的内接四边形ABCD中,∠BCD=130°,则∠BOD的度数是__________.
答案:.
第6题. 一条弧所对的圆周角为80°,它所对的圆心角是____度,它所含的圆周角是____度.
答案:160,100.
第7题. 如图,在⊙O中,AB是直径,弦CD//AB,的度数为20°,则圆周角∠CPD的度数为_________.
答案:70°.
第8题. 在同圆或等圆中,如果两个圆心角、两条弧、 或
中有一组是相等,那么,所对应的其余各组量都分别相等.
答案:两条弦,两条弦的弦心距.
第9题. 已知AC.BC是⊙O的两条弦,且AC⊥BC,AC=12cm,BC=6cm,则⊙O的直径是_________,弦BC的弦心距是_________.
答案:6cm,6cm.
第10题. 同弧所对的圆心角的度数是它所对圆周角度数的_____倍.
答案:2.
第11题. AB为⊙O的直径,C、D为半圆AB上两点,且弧AC、弧CD、弧DB的度数的比为3∶2∶5,则∠AOC=_____°,∠COD=_____°,∠DOB=_____°.
答案:,,.
第12题. 一条弧所含的圆周角为80°,它所对的圆周角是___度,它所对的圆心角是___度.
答案:100,200.
第13题. 如果一个三角形的一条中线具有以下特点时:_________________,这个三角形就是直角三角形.
答案:一边的中线等于这条边的一半.
第14题. 如图,在△ABC中,以BC为直径的⊙O交AB于D,交AC于E,BD=CE.
求证:AB=AC
答案:作BD、CE的弦心距证明.
第15题. 请你根据所学的知识提出猜想,四边形ABCD满足什么条件时存在外接圆 .
答案:此题为开放题目,以下条件之一均可
(1) ∠BAD+∠BCD=180° (2) ∠ABC+∠ADC=180°
(3) ∠CAD=∠CBD (4) ∠BAC=∠BDC
(5) ∠ACB=∠ADB (6) ∠ACD=∠ABD
第16题. 如图,在△ABC中,∠A=15°,∠B=30°,AB=10,试求
△ABC外接圆的半径.
答案:∠C =135°,优弧度数为270°,,劣弧的度数为90°,AB所对的圆心角为90°,所以半径=.
第17题. AB=AC=AD,试证明:∠BAC=2∠BDC.
答案:以A为圆心,以AB为半径作圆,C、D均在⊙A上,所以,∠BAC=2∠BDC.
第18题. 下图所示的角中,圆周角是( )
答案:D.
第19题. 若一个圆内接四边形ABCD中,∠A:∠B:∠C=1:2:3,则( )
A.∠A=∠C B.∠B=2∠C C.∠B=∠D D.∠A=2∠C
答案:C.
第20题. 在半径为5的圆内,有一条长为5的弦,则此弦所对的圆周角为( )
A.60°或120° B.30°或150° C.60° D.120
答案:A.
第21题. 如图,已知圆心角∠AOB=120°,则圆周角∠ACB的度数是( )
A.60° B.100° C.120° D.80°
答案:A.
第22题. 如图,AB是⊙O的直径,∠C=30°.则∠ABD等于( )
A.30° B.40° C.50° D.60°
答案:D.
第23题. 如图,已知圆心角∠AOB=,则圆周角∠ACB的度数为( )
A. B. C. D.
答案:C.
第24题. 如图,四边形ABCD内接于⊙O,若∠BOD=140°,则∠BCD等于( )
A.140° B.110° C.70° D.20°
答案:B.
第25题. 若圆的一条弦把圆分成度数的比为1∶3的两条弧,则劣弧所对的圆周角等于( )
A.45° B.90° C.135° D.270°
答案:A.
第26题. 如图,A、B、C、D是同一圆上的四个点,且,BA和CD的延长线交于P点,∠P=40°,则∠ACD的度数是( )
A.15° B.20° C.40° D.50°
答案:A.
第27题. 如图,在⊙O中,弦BC//半径OA,AC与OB相交于M,∠C=20°,则∠AMB的度数为( )
A.30° B.60° C.50° D.40°
答案:B.
第28题. 如图,A、B、C、D、E都是⊙O上的点,AB=BC=CD,∠BCD=130°
求∠AED的度数.
答案:AB=BC=CD,故,∠BCD=130°,故的度数为260°,与的度数和为100°,可得的度数为150°,所以,∠AED=75°.
第29题. 如图,在⊙O的内接四边形ABCD中,∠BCD=130°,则∠BOD的度数是__________.
答案:.
第30题. 一条弧所对的圆周角为80°,它所对的圆心角是____度,它所含的圆周角是____度.
答案:,
第31题. 已知AC、BC是⊙O的两条弦,且AC⊥BC,AC=12cm,BC=6cm,则⊙O的直径是_________,弦BC的弦心距是_________.
答案:6cm,6cm.
第32题. 一条弧所含的圆周角为80°,它所对的圆周角是___度,它所对的圆心角是___度.
答案:100,200.
第33题. 一条弧分圆为5∶7两部分,则这两条弦所对的圆周角的度数为________.
答案:75°或105°.
第34题. 如果一个三角形的一条中线具有以下特点时:_________________,这个三角形就是直角三角形.
答案:一边的中线等于这条边的一半.
第35题. 如图,四边形ABCD内接于⊙O,∠BOD=160°,则∠BAD的度数是_______,∠BCD的度数是_______.
答案:.
第36题. 如图,的度数为,那么圆周角∠ACB=_______.
答案:.
第37题. 如图AB.CD是⊙O的两条弦,则图中共有_______个圆周角.
答案:12.
第38题. 如图,在⊙O中,AB⊥CD,OE⊥BC与E,试证明:AD=2OE.
答案:A点的直径AM,连结DM、BM,AB⊥BM,作OF⊥DM于F,便可得CD//BM,所以,,于是BC=DM,OE=OF,OF是△ABC的中位线,AD=2OF,所以,AD=2OE.
第39题. 如图,四边形ABCD内接于⊙O,若∠BCD=100°,则∠BOD等于( )
A.100° B.160° C.80° D.120°
答案:B.
第40题. 如图,在⊙O中,OA=AB=BC,且OB⊥BC,则弧BD和弧DE的度数分别是 ( )
A.15°、15° B.15°、30°
C.30°、15° D.22°30′、22°30′
答案:C.
第41题. 已知:四边形ABCD的四个顶点在同一个圆上,对角线AC⊥BD,AB>CD.若CD=4,则AB与圆的距离为 ( )
A. B.2 C. D.
答案:B.
第42题. ⊙O中,AB是弦,∠OAB=50°,则弦AB所对的圆心角的度数是_________,弦AB所对的弧的度数为_________.
答案:80°,80°或280°.
第43题. 长为3的弦所对的圆周角为135°,则此圆的直径为_________.
答案:.
第44题. ⊙O的半径是5,两条弦AB=CD=8,并且AB⊥CD,垂足为P,则OP的长为___________.
答案:.
第45题. 已知:如图,EF为⊙O的直径,过EF上一点P作弦AB、CD,且∠APF=∠CPF.
求证:PA=PC.
答案:作AB、CD的弦心距OM、ON,进一步证明△OMP≌△ONP(ASA),
得到PM=PN(②);①+②即能证明结论.
第46题. 在⊙O中,OC是半径,弦EF过OC的中点,且垂直于OC,则弦EF所对的圆心角的度数是_________,如果半径为1,弦EF的长是_________.
答案:,.
第47题. 如图,弦AC、BD交于E点,且,∠BEC=130°,那么∠ACD=_________.
答案:105°.
第48题. 如图,如果⊙O的半径为2,弦AB=,那么弦心距OE的长为( )
A. B. C. D.
答案:C.
C
B
D
O
A
O
C
B
D
A
E
C
D
B
A
B
C
A
C
B
D
A
A
B
C
D
C
B
D
O
A
O
A
B
D
C
O
A
C
B
D
E
A
B
C
D
A
O
B
E
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
同课章节目录
- 第十八章 相似形
- 18.1 比例线段
- 18.2 黄金分割
- 18.3 平行线分三角形两边成比例
- 18.4 相似多边形
- 18.5 相似三角形的判定
- 18.6 相似三角形的性质
- 18.7 应用举例
- 第十九章 二次函数和反比例函数
- 19.1 二次函数
- 19.2 二次函数 y=ax2+bx+c(a≠0) 的图象
- 19.3 二次函数的性质
- 19.4 二次函数的应用
- 19.5 反比例函数
- 19.6 反比例函数的图象、性质和应用
- 第二十章 解直角三角形
- 20.1 锐角三角函数
- 20.2 30°、45°、60° 角的三角函数值
- 20.3 用科学计算器求锐角三角函数值
- 20.4 解直角三角形
- 20.5 测量与计算
- 第二十一章 圆(上)
- 21.1 圆的有关概念
- 21.2 过三点的圆
- 21.3 圆的对称性
- 21.4 圆周角
- 第二十二章 圆(下)
- 22.1 直线和圆的位置关系
- 22.2 圆的切线
- 22.3 正多边形的有关计算
