第十九章 一次函数单元检测试题(含答案)
图片预览

文档简介
中小学教育资源及组卷应用平台
第19章《一次函数》单元测试
一.选择题(每题3分,共30分)
1.函数 的自变量x的取值范围是( )
A. B. C. 且 D. 且
2.一次函数y=kx+|k-2|的图象过点(0,3),且y随x的增大而减小,则k的值为( )
A.-1 B.5 C.5或-1 D.-5
3.某登山队大本营所在地的气温为.海拔每升高,气温下降.队员由大本营向上登高,气温为,则y与x的函数关系式为( )
A. B. C. D.
4. 如果的自变量增加4,函数值相应地减少16,则的值为( )
A.4 B.- 4 C. D.
5. 变量x,y有如下的关系,其中y是x的函数的是 ( )
A.y2=8x B.|y|=x C.y= D.x=y4
6.若一次函数y=(3-k)x-k的图象经过第二、三、四象限,则k的取值范围是( )
A.k>3 B.07.如果通过平移直线得到的图象,那么直线必须( ).
A.向上平移5个单位 B.向下平移5个单位
C.向上平移个单位 D.向下平移个单位
8.如图,正方形ABCD的边长为4,现有一动点P从点A出发,沿A→B→C→D→A的路径以每秒1个单位长度的速度匀速运动,设点P运动的时间为t,△APB的面积为S,则下列图象能大致反映S与t的函数关系的是( )
A.B.C. D.
9.小苏现已存款180元.为赞助“希望工程”,她计划今后每月存款10元,则存款总金额(元)与时间(月)之间的关系式是( )
A. B. C. D.
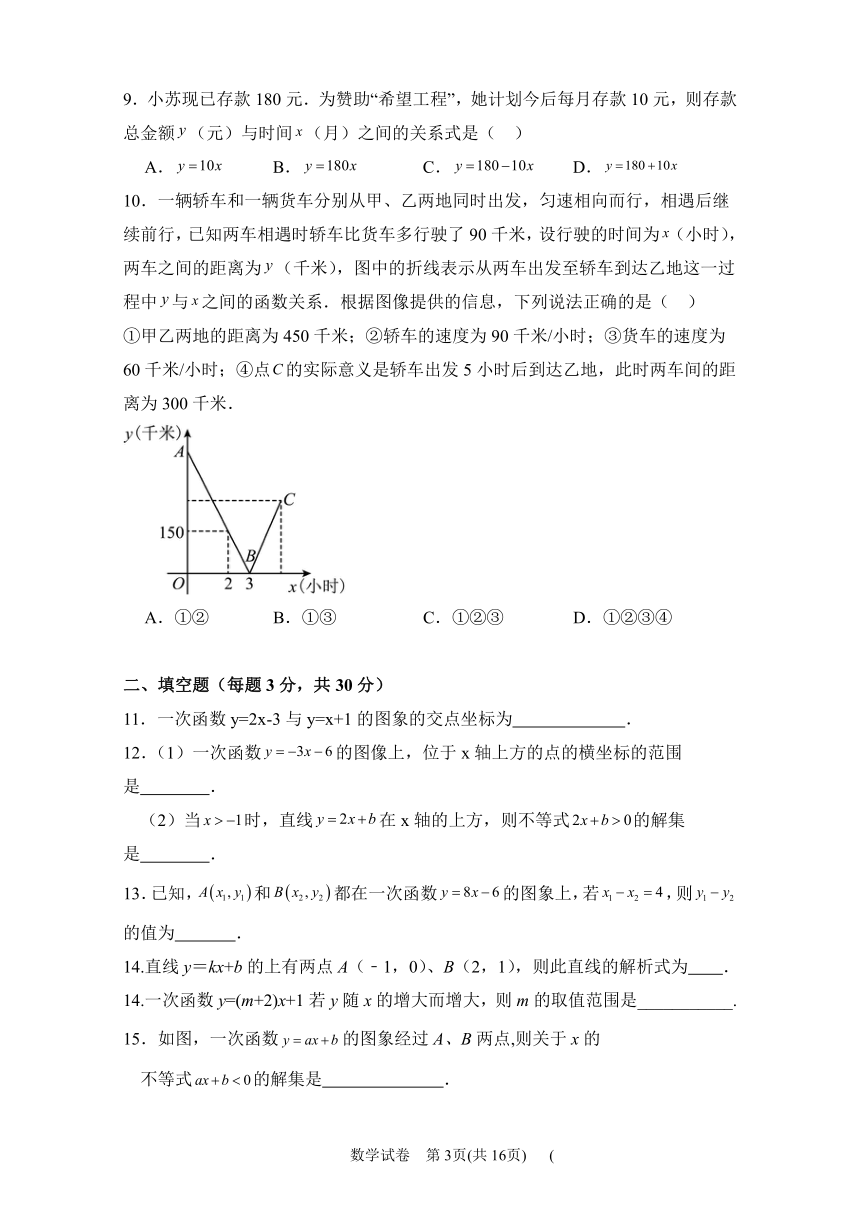
10.一辆轿车和一辆货车分别从甲、乙两地同时出发,匀速相向而行,相遇后继续前行,已知两车相遇时轿车比货车多行驶了90千米,设行驶的时间为(小时),两车之间的距离为(千米),图中的折线表示从两车出发至轿车到达乙地这一过程中与之间的函数关系.根据图像提供的信息,下列说法正确的是( )
①甲乙两地的距离为450千米;②轿车的速度为90千米/小时;③货车的速度为60千米/小时;④点的实际意义是轿车出发5小时后到达乙地,此时两车间的距离为300千米.
A.①② B.①③ C.①②③ D.①②③④
二、填空题(每题3分,共30分)
11.一次函数y=2x-3与y=x+1的图象的交点坐标为 .
12.(1)一次函数的图像上,位于x轴上方的点的横坐标的范围是 .
(2)当时,直线在x轴的上方,则不等式的解集是 .
13.已知,和都在一次函数的图象上,若,则的值为 .
14.直线y=kx+b的上有两点A(﹣1,0)、B(2,1),则此直线的解析式为 .
14.一次函数y=(m+2)x+1若y随x的增大而增大,则m的取值范围是___________.
15.如图,一次函数的图象经过A、B两点,则关于x的
不等式的解集是 .
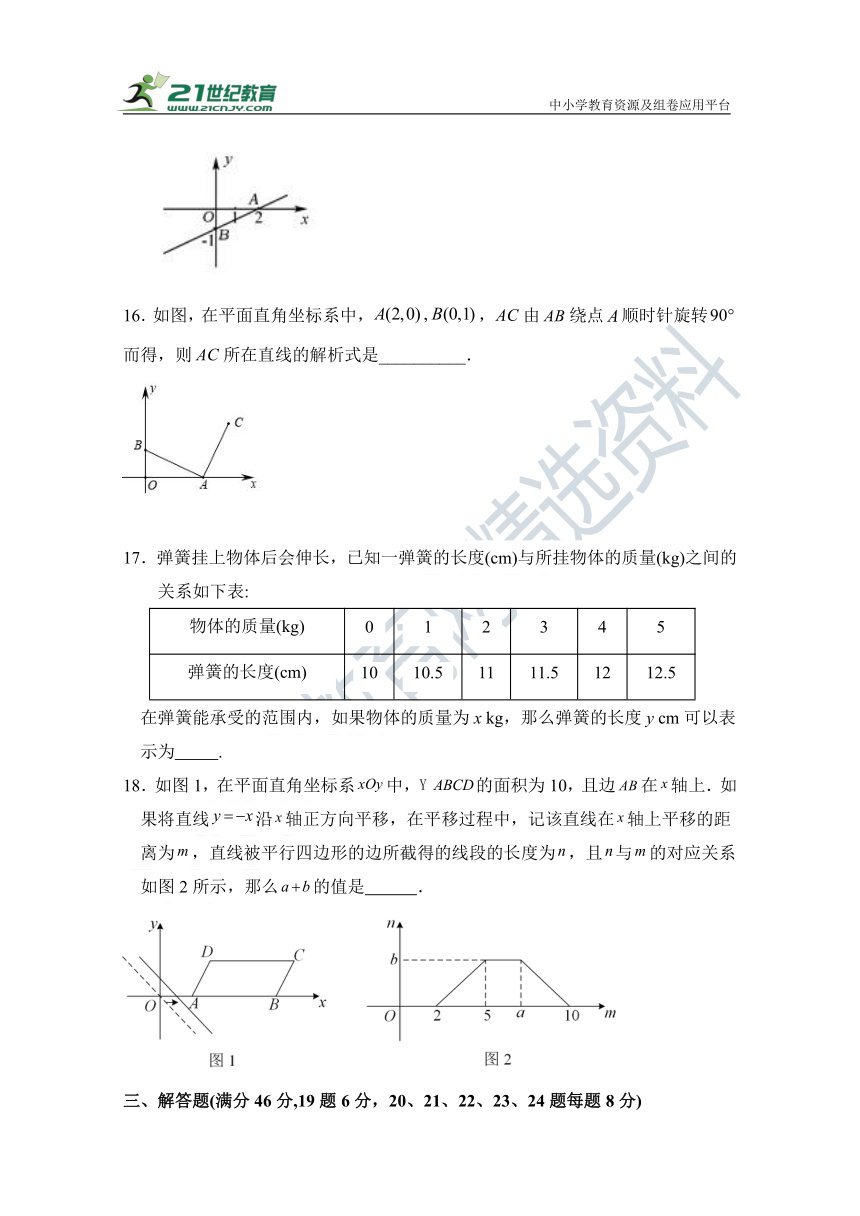
16.如图,在平面直角坐标系中,,由绕点顺时针旋转而得,则所在直线的解析式是__________.
17.弹簧挂上物体后会伸长,已知一弹簧的长度(cm)与所挂物体的质量(kg)之间的关系如下表:
物体的质量(kg) 0 1 2 3 4 5
弹簧的长度(cm) 10 10.5 11 11.5 12 12.5
在弹簧能承受的范围内,如果物体的质量为x kg,那么弹簧的长度y cm可以表示为 .
18.如图1,在平面直角坐标系中,的面积为10,且边在轴上.如果将直线沿轴正方向平移,在平移过程中,记该直线在轴上平移的距离为,直线被平行四边形的边所截得的线段的长度为,且与的对应关系如图2所示,那么的值是 .
三、解答题(满分46分,19题6分,20、21、22、23、24题每题8分)
19.已知, ,画出函数图像并根据图像回答下列问题:
(1)当时,x______; (2)当时,x_______;
(3)当时,x_______; (4)当时,x________;
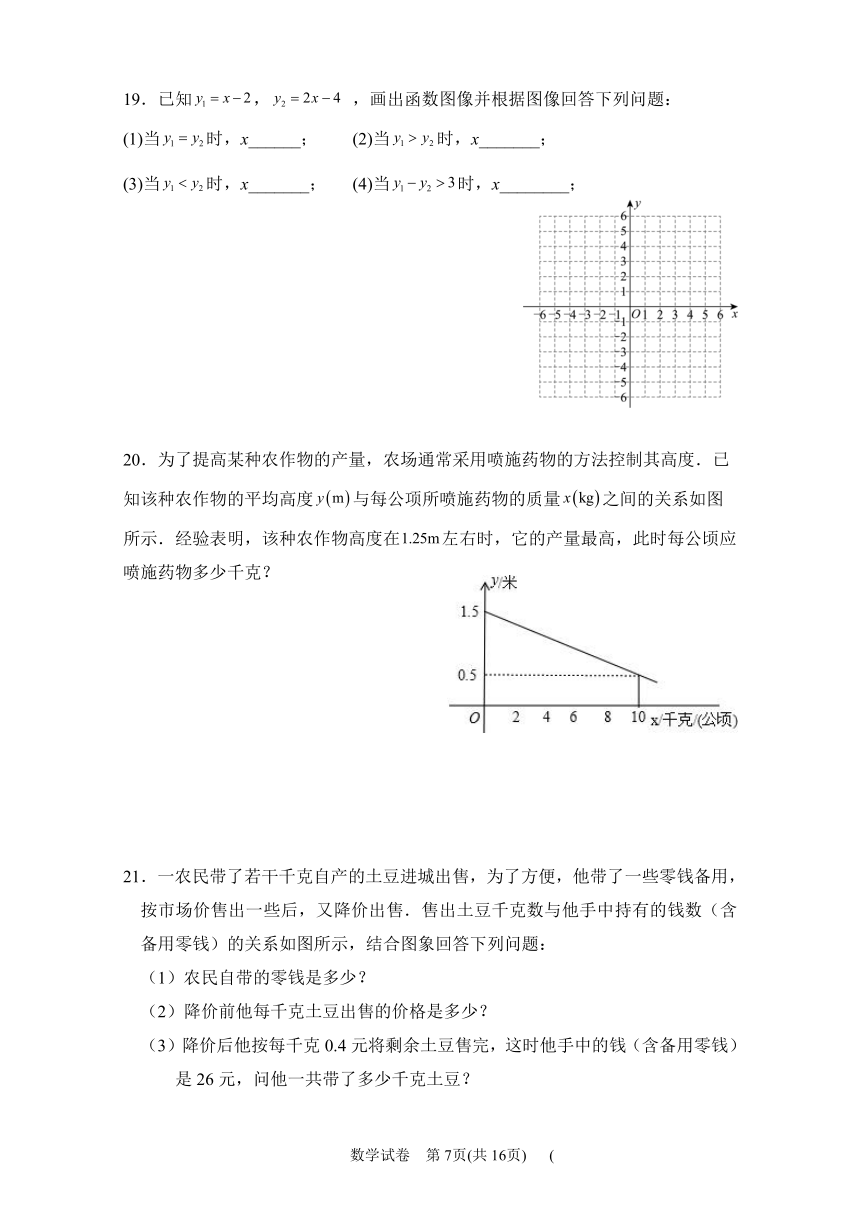
20.为了提高某种农作物的产量,农场通常采用喷施药物的方法控制其高度.已知该种农作物的平均高度与每公项所喷施药物的质量之间的关系如图所示.经验表明,该种农作物高度在左右时,它的产量最高,此时每公顷应喷施药物多少千克?
21.一农民带了若干千克自产的土豆进城出售,为了方便,他带了一些零钱备用,按市场价售出一些后,又降价出售.售出土豆千克数与他手中持有的钱数(含备用零钱)的关系如图所示,结合图象回答下列问题:
(1)农民自带的零钱是多少?
(2)降价前他每千克土豆出售的价格是多少?
(3)降价后他按每千克0.4元将剩余土豆售完,这时他手中的钱(含备用零钱)是26元,问他一共带了多少千克土豆?
22.如图所示的折线ABC表示从甲地向乙地打长途电话所需的电话费y(元)与通话时间t(分钟)之间的函数关系的图象.(1)写出y与t之间的函数关系式.(2)通话2分钟应付通话费多少元?通话7分钟呢?
23.参观红色基地,研学红色文化.根据校团委的部署,八年级名师生准备租车到革命历史展览馆参观学习.车站有大小两种车型,每辆大车可坐人,每辆小车可坐人,已知租用大车1辆和小车2辆共需元,租用大车2辆和小车1辆共需元.
(1)租大车、小车两种客车每辆各多少元?
(2)若学校计划租辆车,其中大车辆有a辆,租车费用w元,能保障所有的八年级师生到革命历史展览馆参观学习,租车费用不超过元,有哪几种租车方案?租车费用最少为多少?
24.某天,甲车间工人加工零件,工作中有一次停产检修机器,然后以原来的工作效率继续加工,由于任务紧急,乙车间加入与甲车间一起生产零件,两组各自加工零件的数量y(个)与甲组加工时间t(时)之间的函数图象如图所示.
(1)求甲组加工零件总量a.
(2)求甲组加工零件的数量y与时间t之间的函数关系式,并写出t的取值范围.
(3)当甲、乙两车间加工零件总数量为300个时,直接写出t的值.
答案:
一、选择题(每题3分,共30分)
题号 1 2 3 4 5 6 7 8 9 10
答案 D A B D D A C B C A
二、填空题(每题3分,共24分)
11.(4,5)
12.
13.32
14.y=x+.
15. X<2
16.
17.y=-x+10.
18. 3820元.
三、解答题(满分46分,19题6分,20、21、22、23、24题每题8分)
19.(1)
(2)
(3)
(4)
20.每公顷应喷施药物约.
21.①5元;②0.5元;③45千克
22.①当03时,y=t-0.6.
②2.4元;6.4元
23.(1)解:设租用大车每辆x元,租用小车每辆y元,
根据题意可列方程组为:,
解得:,
答:租用大客车每辆元,租用小客车每辆元;
(2)解:根据题意可得:租用乙种客车辆,且
,
解得:,
根据题意可得:,
∵,
∴w随a的增大而增大,
∵,a取整数,
∴,6,7,
∴当时,w有最小值,此时最小值为元.
答:当大车租用5辆,小车租辆时,能保障所有师生送到展览馆且租车费用最少,最少费用为元.
24.(1)解:∵甲车间的效率不变,在前三分钟内生产了120个,
∴甲车间的效率为每小时120÷3=40(个),
∴甲车间的生产总量为a=120+(8-4)×40=280(个);
(2)解:当时,
当时,
当时,
∴甲组加工零件的数量y与时间t之间的函数关系式为
(3)
数学试卷 第15页(共16页) ( 数学试卷 第16页(共16页)
第19章《一次函数》单元测试
一.选择题(每题3分,共30分)
1.函数 的自变量x的取值范围是( )
A. B. C. 且 D. 且
2.一次函数y=kx+|k-2|的图象过点(0,3),且y随x的增大而减小,则k的值为( )
A.-1 B.5 C.5或-1 D.-5
3.某登山队大本营所在地的气温为.海拔每升高,气温下降.队员由大本营向上登高,气温为,则y与x的函数关系式为( )
A. B. C. D.
4. 如果的自变量增加4,函数值相应地减少16,则的值为( )
A.4 B.- 4 C. D.
5. 变量x,y有如下的关系,其中y是x的函数的是 ( )
A.y2=8x B.|y|=x C.y= D.x=y4
6.若一次函数y=(3-k)x-k的图象经过第二、三、四象限,则k的取值范围是( )
A.k>3 B.0
A.向上平移5个单位 B.向下平移5个单位
C.向上平移个单位 D.向下平移个单位
8.如图,正方形ABCD的边长为4,现有一动点P从点A出发,沿A→B→C→D→A的路径以每秒1个单位长度的速度匀速运动,设点P运动的时间为t,△APB的面积为S,则下列图象能大致反映S与t的函数关系的是( )
A.B.C. D.
9.小苏现已存款180元.为赞助“希望工程”,她计划今后每月存款10元,则存款总金额(元)与时间(月)之间的关系式是( )
A. B. C. D.
10.一辆轿车和一辆货车分别从甲、乙两地同时出发,匀速相向而行,相遇后继续前行,已知两车相遇时轿车比货车多行驶了90千米,设行驶的时间为(小时),两车之间的距离为(千米),图中的折线表示从两车出发至轿车到达乙地这一过程中与之间的函数关系.根据图像提供的信息,下列说法正确的是( )
①甲乙两地的距离为450千米;②轿车的速度为90千米/小时;③货车的速度为60千米/小时;④点的实际意义是轿车出发5小时后到达乙地,此时两车间的距离为300千米.
A.①② B.①③ C.①②③ D.①②③④
二、填空题(每题3分,共30分)
11.一次函数y=2x-3与y=x+1的图象的交点坐标为 .
12.(1)一次函数的图像上,位于x轴上方的点的横坐标的范围是 .
(2)当时,直线在x轴的上方,则不等式的解集是 .
13.已知,和都在一次函数的图象上,若,则的值为 .
14.直线y=kx+b的上有两点A(﹣1,0)、B(2,1),则此直线的解析式为 .
14.一次函数y=(m+2)x+1若y随x的增大而增大,则m的取值范围是___________.
15.如图,一次函数的图象经过A、B两点,则关于x的
不等式的解集是 .
16.如图,在平面直角坐标系中,,由绕点顺时针旋转而得,则所在直线的解析式是__________.
17.弹簧挂上物体后会伸长,已知一弹簧的长度(cm)与所挂物体的质量(kg)之间的关系如下表:
物体的质量(kg) 0 1 2 3 4 5
弹簧的长度(cm) 10 10.5 11 11.5 12 12.5
在弹簧能承受的范围内,如果物体的质量为x kg,那么弹簧的长度y cm可以表示为 .
18.如图1,在平面直角坐标系中,的面积为10,且边在轴上.如果将直线沿轴正方向平移,在平移过程中,记该直线在轴上平移的距离为,直线被平行四边形的边所截得的线段的长度为,且与的对应关系如图2所示,那么的值是 .
三、解答题(满分46分,19题6分,20、21、22、23、24题每题8分)
19.已知, ,画出函数图像并根据图像回答下列问题:
(1)当时,x______; (2)当时,x_______;
(3)当时,x_______; (4)当时,x________;
20.为了提高某种农作物的产量,农场通常采用喷施药物的方法控制其高度.已知该种农作物的平均高度与每公项所喷施药物的质量之间的关系如图所示.经验表明,该种农作物高度在左右时,它的产量最高,此时每公顷应喷施药物多少千克?
21.一农民带了若干千克自产的土豆进城出售,为了方便,他带了一些零钱备用,按市场价售出一些后,又降价出售.售出土豆千克数与他手中持有的钱数(含备用零钱)的关系如图所示,结合图象回答下列问题:
(1)农民自带的零钱是多少?
(2)降价前他每千克土豆出售的价格是多少?
(3)降价后他按每千克0.4元将剩余土豆售完,这时他手中的钱(含备用零钱)是26元,问他一共带了多少千克土豆?
22.如图所示的折线ABC表示从甲地向乙地打长途电话所需的电话费y(元)与通话时间t(分钟)之间的函数关系的图象.(1)写出y与t之间的函数关系式.(2)通话2分钟应付通话费多少元?通话7分钟呢?
23.参观红色基地,研学红色文化.根据校团委的部署,八年级名师生准备租车到革命历史展览馆参观学习.车站有大小两种车型,每辆大车可坐人,每辆小车可坐人,已知租用大车1辆和小车2辆共需元,租用大车2辆和小车1辆共需元.
(1)租大车、小车两种客车每辆各多少元?
(2)若学校计划租辆车,其中大车辆有a辆,租车费用w元,能保障所有的八年级师生到革命历史展览馆参观学习,租车费用不超过元,有哪几种租车方案?租车费用最少为多少?
24.某天,甲车间工人加工零件,工作中有一次停产检修机器,然后以原来的工作效率继续加工,由于任务紧急,乙车间加入与甲车间一起生产零件,两组各自加工零件的数量y(个)与甲组加工时间t(时)之间的函数图象如图所示.
(1)求甲组加工零件总量a.
(2)求甲组加工零件的数量y与时间t之间的函数关系式,并写出t的取值范围.
(3)当甲、乙两车间加工零件总数量为300个时,直接写出t的值.
答案:
一、选择题(每题3分,共30分)
题号 1 2 3 4 5 6 7 8 9 10
答案 D A B D D A C B C A
二、填空题(每题3分,共24分)
11.(4,5)
12.
13.32
14.y=x+.
15. X<2
16.
17.y=-x+10.
18. 3820元.
三、解答题(满分46分,19题6分,20、21、22、23、24题每题8分)
19.(1)
(2)
(3)
(4)
20.每公顷应喷施药物约.
21.①5元;②0.5元;③45千克
22.①当0
②2.4元;6.4元
23.(1)解:设租用大车每辆x元,租用小车每辆y元,
根据题意可列方程组为:,
解得:,
答:租用大客车每辆元,租用小客车每辆元;
(2)解:根据题意可得:租用乙种客车辆,且
,
解得:,
根据题意可得:,
∵,
∴w随a的增大而增大,
∵,a取整数,
∴,6,7,
∴当时,w有最小值,此时最小值为元.
答:当大车租用5辆,小车租辆时,能保障所有师生送到展览馆且租车费用最少,最少费用为元.
24.(1)解:∵甲车间的效率不变,在前三分钟内生产了120个,
∴甲车间的效率为每小时120÷3=40(个),
∴甲车间的生产总量为a=120+(8-4)×40=280(个);
(2)解:当时,
当时,
当时,
∴甲组加工零件的数量y与时间t之间的函数关系式为
(3)
数学试卷 第15页(共16页) ( 数学试卷 第16页(共16页)
