人教版七年级数学下册压轴题专项讲练专题 7.2平面直角坐标系中的规律问题(原卷版+解析版)
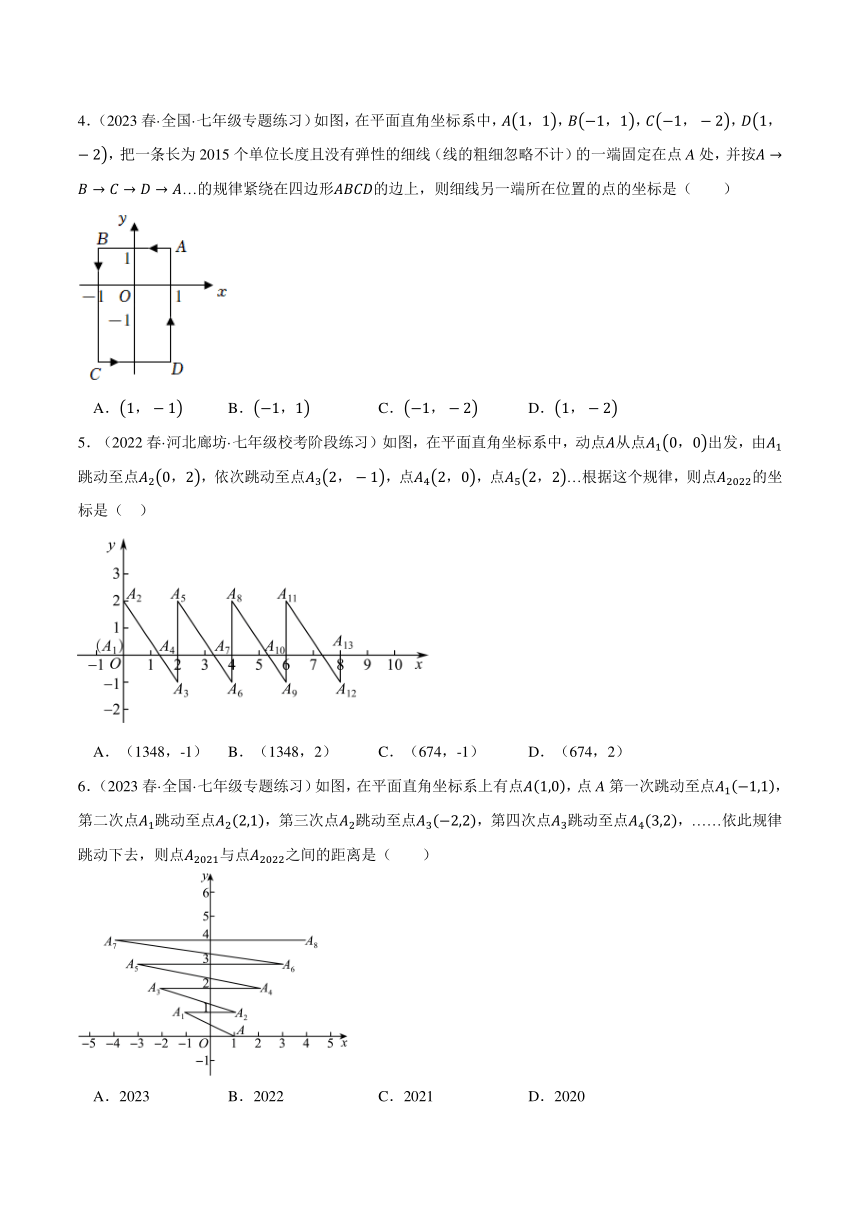
文档属性
| 名称 | 人教版七年级数学下册压轴题专项讲练专题 7.2平面直角坐标系中的规律问题(原卷版+解析版) |  | |
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-27 22:18:59 | ||
图片预览


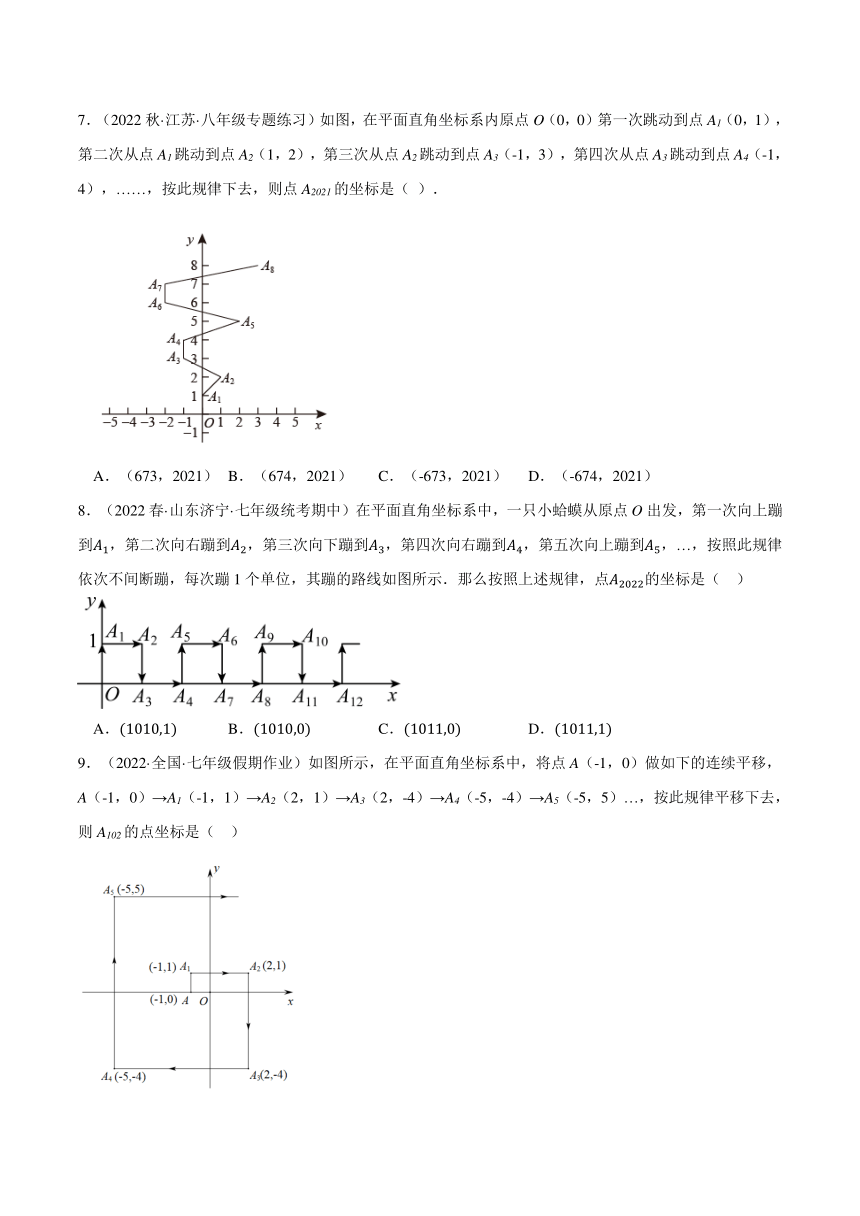
文档简介
专题7.1 平面直角坐标系中的规律问题
【典例1】综合与实践:
(1)动手探索在平面直角坐标系内,已知点,,,,连接,,,,,并依次取,,,,的中点,,,,,分别写出,,,的坐标;
(2)观察归纳以上各线段两端点的横、纵坐标与该线段中点的横、纵坐标之间的对应关系,猜想:若线段两端点坐标分别为、,线段的中点是,请用等式表示你所观察的规律 ,并用,的坐标验证规律是否正确 (填“是”或“否” ;
(3)实践运用利用上面探索得到的规律解决问题:
①若点,点,则线段的中点的坐标为 ;
②已知点是线段的中点,且点,,求点的坐标.
【思路点拨】
(1)根据图形可以直接读取坐标即可得到答案;
(2)根据观察得到规律并写出等式,再利用B、C、D、G、I五点坐标即可验证所得规律,得到答案;
(3)①根据(2)中发现的规律,即可得到线段的中点的坐标;
②设点的坐标为,根据根据(2)中发现的规律解方程求解即可得到点的坐标.
【解题过程】
(1)解:根据图形可以直接读取各点坐标,,,,,,
,,,的坐标分别为:,,,;
(2)解:根据各点坐标可以发现,线段中点坐标的纵坐标值为线段两端点纵坐标和的一半,线段中点坐标的横坐标值为线段两端点横坐标和的一半,
、,线段的中点是,
,
,,,,,、分别为线段、的中点,
检验得,,,
通过,的坐标验证规律是正确的,
故答案为:;是;
(3)解:①点,点,
根据(2)中发现的规律,线段的中点的坐标为,
故答案为:;
②设点的坐标为,
点是线段的中点,且点,,
,
,
点的坐标为.
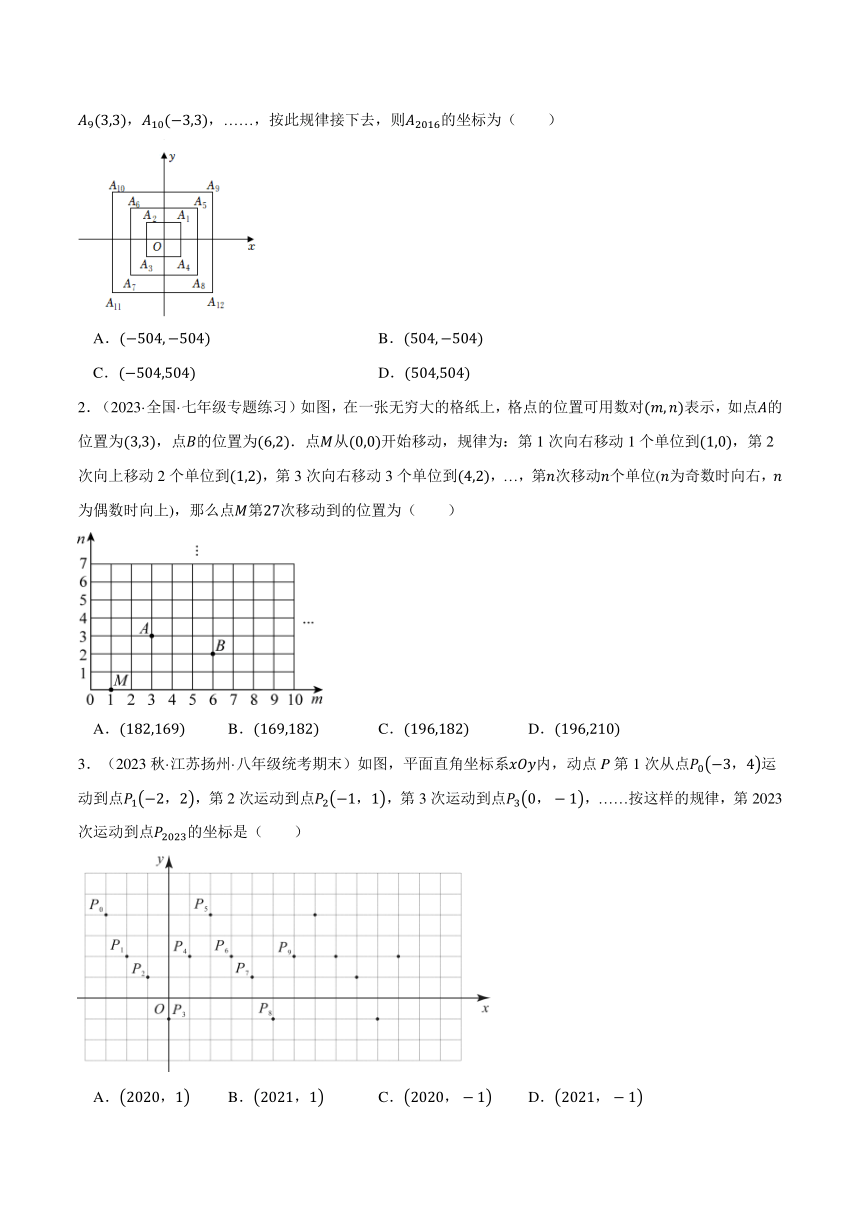
1.(2023春·全国·七年级专题练习)如图,正方形的边长依次为2,4,6,8,……,他们在直角坐标系中的位置如图所示,其中,,,,,,,,,,……,按此规律接下去,则的坐标为( )
A. B.
C. D.
2.(2023·全国·七年级专题练习)如图,在一张无穷大的格纸上,格点的位置可用数对表示,如点的位置为,点的位置为.点从开始移动,规律为:第1次向右移动1个单位到,第2次向上移动2个单位到,第3次向右移动3个单位到,…,第次移动个单位(为奇数时向右,为偶数时向上),那么点第次移动到的位置为( )
A. B. C. D.
3.(2023秋·江苏扬州·八年级统考期末)如图,平面直角坐标系内,动点P第1次从点运动到点,第2次运动到点,第3次运动到点,……按这样的规律,第2023次运动到点的坐标是( )
A. B. C. D.
4.(2023春·全国·七年级专题练习)如图,在平面直角坐标系中,,,,,把一条长为2015个单位长度且没有弹性的细线(线的粗细忽略不计)的一端固定在点A处,并按…的规律紧绕在四边形的边上,则细线另一端所在位置的点的坐标是( )
A. B. C. D.
5.(2022春·河北廊坊·七年级校考阶段练习)如图,在平面直角坐标系中,动点从点出发,由跳动至点,依次跳动至点,点,点…根据这个规律,则点的坐标是( )
A.(1348,-1) B.(1348,2) C.(674,-1) D.(674,2)
6.(2023春·全国·七年级专题练习)如图,在平面直角坐标系上有点,点A第一次跳动至点,第二次点跳动至点,第三次点跳动至点,第四次点跳动至点,……依此规律跳动下去,则点与点之间的距离是( )
A.2023 B.2022 C.2021 D.2020
7.(2022秋·江苏·八年级专题练习)如图,在平面直角坐标系内原点O(0,0)第一次跳动到点A1(0,1),第二次从点A1跳动到点A2(1,2),第三次从点A2跳动到点A3(-1,3),第四次从点A3跳动到点A4(-1,4),……,按此规律下去,则点A2021的坐标是( ).
A.(673,2021) B.(674,2021) C.(-673,2021) D.(-674,2021)
8.(2022春·山东济宁·七年级统考期中)在平面直角坐标系中,一只小蛤蟆从原点O出发,第一次向上蹦到,第二次向右蹦到,第三次向下蹦到,第四次向右蹦到,第五次向上蹦到,…,按照此规律依次不间断蹦,每次蹦1个单位,其蹦的路线如图所示.那么按照上述规律,点的坐标是( )
A. B. C. D.
9.(2022·全国·七年级假期作业)如图所示,在平面直角坐标系中,将点A(-1,0)做如下的连续平移,A(-1,0)→A1(-1,1)→A2(2,1)→A3(2,-4)→A4(-5,-4)→A5(-5,5)…,按此规律平移下去,则A102的点坐标是( )
A. B. C. D.
10.(2023秋·山东东营·七年级统考期末)如图,已知A1(1,2),A2(2,2),A3(3,0),A4(4,﹣2),A5(5,﹣2),A6(6,0),…,按这样的规律,则点A2022的坐标为______.
11.(2023·全国·九年级专题练习)如图,动点P在平面直角坐标系中按图中箭头所示方向运动,第1次从原点运动到点,第2次接着运动到点,第3次接着运动到点,按这样的运动规律,经过第2017次运动后,动点P的坐标是______,经过第2018次运动后,动点P的坐标是______.
12.(2022秋·浙江·八年级专题练习)如图,已知点的坐标是,线段从原点出发后,在第一象限内按如下有规律的方式前行:,;,;,;…;则点的坐标是______.
13.(2023春·七年级单元测试)如图,在平面直角坐标系中,点A从依次跳动到,,,,,,,,,,…,按此规律,则点的坐标是______________
14.(2022秋·河北邯郸·八年级校考开学考试)如图,在平面直角坐标系中,有若干个整数点,其顺序按图中“”方向排列,如,,,,,,根据这个规律探索可得,第个点的坐标为______,第个点的坐标为______.
15.(2022春·北京·七年级北京市第五中学分校校考期末)如图,在平面直角坐标系中,点.点第1次向上跳动1个单位至点,紧接着第2次向左跳动2个单位至点,第3次向上跳动1个单位至点,第4次向右跳动3个单位至点,第5次又向上跳动1个单位至点,第6次向左跳动4个单位至点,…照此规律,点第2022次跳动至点的坐标是________.
16.(2022春·山东青岛·八年级校考期中)如图所示,一个机器人从O点出发,向正东方向走到达点,再向正北方向走到达点,再向正西方向走到达点,再向正南方向走到达点,再向正东方向走到达点,按照此规律走下去,相对于点O,机器人走到时,点的坐标是______,点的坐标是______.
17.(2022秋·全国·八年级专题练习)如图,在平面直角坐标系中,有若干个整数点.其顺序按照图中“→”方向排列,即,,,,,…….根据这个规律,探究可得到第110个点的坐标为______.
18.(2023秋·湖北孝感·九年级校考期末)如图,在平面直角坐标系中,有若干个横纵坐标分别为整数的点,其顺序为,,,,,,…,根据这个规律,第25个点的坐标为________,第2022个点的坐标为________.
19.(2022春·河北邢台·七年级校考期末)如图,在平面直角坐标系中,轴,轴,点,,,在轴上,,,,,.
(1)若点在线段上,当点与点的距离最小时,点的坐标为____;
(2)把一条长为2022个单位长度且无弹性的细线(粗细忽略不计)的一端固定在处,并按的规律紧绕在图形“凸”的边上,则细线的另一端所在位置的点的坐标为____.
20.(2022秋·全国·八年级专题练习)小明在学面直角坐标系后,突发奇想,画出了这样的图形(如图).他把图形与x轴正半轴的交点依次记作,,…,,图形与y轴正半轴的交点依次记作,,…,,图形与x轴负半轴的交点依次记作,,…,,图形与y轴负半轴的交点依次记作,,…,,发现其中包含了一定的数学规律.
请根据你发现的规律完成下列题目:
(1)请分别写出下列点的坐标:__________,__________,__________,__________.
(2)请分别写出下列点的坐标:__________,__________,__________,__________.
(3)请求出四边形的面积.
专题7.1 平面直角坐标系中的规律问题
【典例1】综合与实践:
(1)动手探索在平面直角坐标系内,已知点,,,,连接,,,,,并依次取,,,,的中点,,,,,分别写出,,,的坐标;
(2)观察归纳以上各线段两端点的横、纵坐标与该线段中点的横、纵坐标之间的对应关系,猜想:若线段两端点坐标分别为、,线段的中点是,请用等式表示你所观察的规律 ,并用,的坐标验证规律是否正确 (填“是”或“否” ;
(3)实践运用利用上面探索得到的规律解决问题:
①若点,点,则线段的中点的坐标为 ;
②已知点是线段的中点,且点,,求点的坐标.
【思路点拨】
(1)根据图形可以直接读取坐标即可得到答案;
(2)根据观察得到规律并写出等式,再利用B、C、D、G、I五点坐标即可验证所得规律,得到答案;
(3)①根据(2)中发现的规律,即可得到线段的中点的坐标;
②设点的坐标为,根据根据(2)中发现的规律解方程求解即可得到点的坐标.
【解题过程】
(1)解:根据图形可以直接读取各点坐标,,,,,,
,,,的坐标分别为:,,,;
(2)解:根据各点坐标可以发现,线段中点坐标的纵坐标值为线段两端点纵坐标和的一半,线段中点坐标的横坐标值为线段两端点横坐标和的一半,
、,线段的中点是,
,
,,,,,、分别为线段、的中点,
检验得,,,
通过,的坐标验证规律是正确的,
故答案为:;是;
(3)解:①点,点,
根据(2)中发现的规律,线段的中点的坐标为,
故答案为:;
②设点的坐标为,
点是线段的中点,且点,,
,
,
点的坐标为.
1.(2023春·全国·七年级专题练习)如图,正方形的边长依次为2,4,6,8,……,他们在直角坐标系中的位置如图所示,其中,,,,,,,,,,……,按此规律接下去,则的坐标为( )
A. B.
C. D.
【思路点拨】
由正方形的中心都是位于原点,边长依次为2,4,6,8,,可得第个正方形的顶点横坐标与纵坐标的绝对值都是.计算,根据商和余数知道是第几个正方形的顶点,且在哪一个象限,进而得出的坐标.
【解题过程】
解:,
顶点是第504个正方形的顶点,且在第四象限,
横坐标是,纵坐标是,
,
故选:B.
2.(2023·全国·七年级专题练习)如图,在一张无穷大的格纸上,格点的位置可用数对表示,如点的位置为,点的位置为.点从开始移动,规律为:第1次向右移动1个单位到,第2次向上移动2个单位到,第3次向右移动3个单位到,…,第次移动个单位(为奇数时向右,为偶数时向上),那么点第次移动到的位置为( )
A. B. C. D.
【思路点拨】
数对表示位置的方法是:第一个表示列,第二个表示行,当向右移动时,列的数字发生变化,行的数字不变,向上移动时,行的数字发生变化,列的数字不变,据此即可得解.
【解题过程】
解:根据题意可知:当向右移动时,列的数字发生变化,行的数字不变,当向上移动时,行的数字发生变化,列的数字不变,
∴点第次移动到的位置时,列的数字是中所有奇数的和,行的数字是中所有偶数的和,
∴,,
∴点第次移动到的位置为,
故选:.
3.(2023秋·江苏扬州·八年级统考期末)如图,平面直角坐标系内,动点P第1次从点运动到点,第2次运动到点,第3次运动到点,……按这样的规律,第2023次运动到点的坐标是( )
A. B. C. D.
【思路点拨】
根据图象可得出:横坐标为运动次数,纵坐标依次为4,2,1,,2,4,每5次一轮,进而即可求出答案.
【解题过程】
解:根据动点在平面直角坐标系中的运动,
,,,,,,
…,
∴横坐标为运动次数,经过第2023次运动后,点的横坐标是2020,
纵坐标依次为4,2,1,,2,每5次一轮,
∴ 4,
∴经过第2023次运动后,点的坐标是,
故选:C.
4.(2023春·全国·七年级专题练习)如图,在平面直角坐标系中,,,,,把一条长为2015个单位长度且没有弹性的细线(线的粗细忽略不计)的一端固定在点A处,并按…的规律紧绕在四边形的边上,则细线另一端所在位置的点的坐标是( )
A. B. C. D.
【思路点拨】
根据点的坐标求出四边形的周长,然后求出另一端是绕第几圈后的第几个单位长度,从而确定答案.
【解题过程】
解:∵,,,,
∴,,,,
∴绕四边形一周的细线长度为,
,
∴细线另一端在绕四边形第202圈的第5个单位长度的位置,即点C的位置,
∴点的坐标为.
故选:C.
5.(2022春·河北廊坊·七年级校考阶段练习)如图,在平面直角坐标系中,动点从点出发,由跳动至点,依次跳动至点,点,点…根据这个规律,则点的坐标是( )
A.(1348,-1) B.(1348,2) C.(674,-1) D.(674,2)
【思路点拨】
观察可知,,,,每三个点为一组,纵坐标为0,2,-1循环,每个循环内横坐标增加2,据此求解即可.
【解题过程】
解:∵动点从点出发,由跳动至点,依次跳动至点,点,点…
∴,,,,每三个点为一组,纵坐标为0,2,-1循环,每个循环内横坐标增加2,
∵,
∴点的纵坐标与点的纵坐标相同,即为-1,点横坐标为,
∴点的坐标为(1348,-1).
故选:A.
6.(2023春·全国·七年级专题练习)如图,在平面直角坐标系上有点,点A第一次跳动至点,第二次点跳动至点,第三次点跳动至点,第四次点跳动至点,……依此规律跳动下去,则点与点之间的距离是( )
A.2023 B.2022 C.2021 D.2020
【思路点拨】
根据图形观察发现,第偶数次跳动至点的坐标,横坐标是次数的一半加上1,纵坐标是次数的一半,奇数次跳动与该偶数次跳动的横坐标的相反数加上1,纵坐标相同,可分别求出点与点的坐标,进而可求出点与点之间的距离.
【解题过程】
解:观察发现,第2次跳动至点的坐标是,
第4次跳动至点的坐标是,
第6次跳动至点的坐标是,
第8次跳动至点的坐标是,
…
第2n次跳动至点的坐标是,
则第2022次跳动至点的坐标是,
第2021次跳动至点的坐标是.
∵点与点的纵坐标相等,
∴点与点之间的距离,
故选:A.
7.(2022秋·江苏·八年级专题练习)如图,在平面直角坐标系内原点O(0,0)第一次跳动到点A1(0,1),第二次从点A1跳动到点A2(1,2),第三次从点A2跳动到点A3(-1,3),第四次从点A3跳动到点A4(-1,4),……,按此规律下去,则点A2021的坐标是( ).
A.(673,2021) B.(674,2021) C.(-673,2021) D.(-674,2021)
【思路点拨】
根据已知点的坐标寻找规律并应用解答即可.
【解题过程】
解:∵A1(0,1),A2(1,2),A3(-1,3),A4(-1,4),
∴A5(2,5),A6(-2,6),A7(-2,7),A8(3,8),
∴A3n-1(n,3n-1),A3n(-n,3n),A3n+1(-n,3n+1)(n为正整数),
∵3×674-1=2021,
∴n=674,所以A 2021(674,2021).
故选B.
8.(2022春·山东济宁·七年级统考期中)在平面直角坐标系中,一只小蛤蟆从原点O出发,第一次向上蹦到,第二次向右蹦到,第三次向下蹦到,第四次向右蹦到,第五次向上蹦到,…,按照此规律依次不间断蹦,每次蹦1个单位,其蹦的路线如图所示.那么按照上述规律,点的坐标是( )
A. B. C. D.
【思路点拨】
根据图象可得移动4次图象完成一个循环,再由2022÷4=505……2,可得点A2022在第505个循环的第2个点的位置,即纵坐标与A1的相同,为1,再由A4(2,0),A8(4,0),A12(6,0),……,可得A4n(2n,0),从而得到A2020的坐标是(1010,0),从而可得出点A2022的坐标.
【解题过程】
解:根据题意得:点A1(0,1),A2(1,1),A3(1,0),A4(2,0),A5(2,1),……
∴每移动4次图象完成一个循环,
∵2022÷4=505……2,
∴点A2022在第505个循环的第2个点的位置,即纵坐标与A1的相同,为1,
∵A4(2,0),A8(4,0),A12(6,0),……,
∴A4n(2n,0),
∴A2020的坐标是(1010,0),
∴A2022的坐标是(1010+1,1),即A2022的坐标是(1011,1).
故选:D.
9.(2022·全国·七年级假期作业)如图所示,在平面直角坐标系中,将点A(-1,0)做如下的连续平移,A(-1,0)→A1(-1,1)→A2(2,1)→A3(2,-4)→A4(-5,-4)→A5(-5,5)…,按此规律平移下去,则A102的点坐标是( )
A. B. C. D.
【思路点拨】
根据题意可知,点A平移时每4次为一个周期,由102÷4=25 2,可知点A102的坐标与A4n+2的点的坐标规律相同,分别求出A2,A6,A10的坐标,找出规律,进而求解即可.
【解题过程】
解:由题意可知,将点A(-1,0)向上平移1个单位长度得到A1(-1,1),再向右平移3个单位长度得到A2(2,1),再向下平移5个单位长度得到A3(2,-4),再向左平移7个单位长度得到A4(-5,-4);再向上平移9个单位长度得到A5(-5,5)…,
∴点A平移时每4次为一个周期.
∵102÷4=25 2,
∴点A102的坐标与A4n+2的点的坐标规律相同.
∵A2(2,1),A6(6,5),A10(10,9),
以此类推,
∴A4n+2(4n+2,4n+1),
∴A102的点坐标是(102,101).
故选:C.
10.(2023秋·山东东营·七年级统考期末)如图,已知A1(1,2),A2(2,2),A3(3,0),A4(4,﹣2),A5(5,﹣2),A6(6,0),…,按这样的规律,则点A2022的坐标为______.
【思路点拨】
观察发现,每6个点形成一个循环,再根据点A6的坐标及2022÷6所得的整数及余数,可计算出点A2022的横坐标,再根据余数对比第一组的相应位置的数可得其纵坐标.
【解题过程】
解:观察发现,每6个点形成一个循环,
∵A6(6,0),
∴OA6=6,
∵2022÷6=337,
∴点A2022的位于第337个循环组的第6个,
∴点A2022的横坐标为6×337=2022,其纵坐标为:0,
∴点A2022的坐标为(2022,0).
故答案为:(2022,0).
11.(2023·全国·九年级专题练习)如图,动点P在平面直角坐标系中按图中箭头所示方向运动,第1次从原点运动到点,第2次接着运动到点,第3次接着运动到点,按这样的运动规律,经过第2017次运动后,动点P的坐标是______,经过第2018次运动后,动点P的坐标是______.
【思路点拨】
观察前几次运动后点的坐标,不难发现动点P的横坐标等于运动的次数,而纵坐标的变化为1,0,2,0,1,0,2,0…,4个一循环;
接下来通过总结得到的规律,再结合2017÷4=504……1,即可求出经过2017次运动后动点P的坐标了,同理可找到2018次运动后动点P的坐标.
【解题过程】
根据动点P在平面直角坐标系中按图中箭头所示方向运动,
第1次从原点运动到点(1,1),
第2次接着运动到点(2,0),
第3次接着运动到点(3,2),
第4次接着运动到点(4,0),
第5次接着运动到点(5,1),
…
∴横坐标为运动次数,经过第2017次运动后,动点P的横坐标为2017,纵坐标为1,0,2,0,每4次一轮,
∴经过第2017次运动后,动点P的纵坐标为:2017÷4=504……1,故纵坐标为四个数中第一个,即1,
∴经过第2017次运动后,动点P的坐标是(2017,1).
∵2018÷4=504……2,
∴经过第2018次运动后,动点P的坐标是(2018,0).
故答案为 , .
12.(2022秋·浙江·八年级专题练习)如图,已知点的坐标是,线段从原点出发后,在第一象限内按如下有规律的方式前行:,;,;,;…;则点的坐标是______.
【思路点拨】
先得出A1(1,2),A2(3,1),A3(4,3),A4(6,2),A5(7,4),A6(9,3)的坐标,观察可得A的纵坐标的规律,然后确定A的横坐标与下标之间的关系即可求解.
【解题过程】
解:A1(1,2),A2(3,1),A3(4,3),A4(6,2),A5(7,4),A6(9,3),…,
可得:
A1横坐标为:×3 2=1,纵坐标为:+1=2;
A3横坐标为:×3 2=4,纵坐标为:+1=3;
A5横坐标为:×3 2=7,纵坐标为:+1=4,…;
∴下标为奇数时,横坐标依次为:1,4,7,…,纵坐标为:2,3,4,…;
∴A2023横坐标为:×3 2=3034,纵坐标为:+1=1013…;
∴A2023的坐标为:(3034,1013),
故答案为:(3034,1013).
13.(2023春·七年级单元测试)如图,在平面直角坐标系中,点A从依次跳动到,,,,,,,,,,…,按此规律,则点的坐标是______________
【思路点拨】
根据图形可以发现规律,从到是一个循环,一个循环周期是10,一个循环后又回到x轴上,且一个循环后横坐标增加4个单位,先求出点的坐标(804,0),再求点的坐标即可.
【解题过程】
解:观察图形可知,n为正整数时,的纵坐标为0,1,3,﹣3
纵坐标为0的点:
纵坐标为1的点:
纵坐标为3的点:
纵坐标为﹣3的点:
可以看出纵坐标为1,3,﹣3时,n取连续的两个数为一组,则10个10个的增加,
∵2021=10×202+1,纵坐标为1的规律
∴的纵坐标为1,
由,解得n=203,
∵正好是往右循环203次,
∴横坐标为﹣4+(203-1)×4=804,
∴点的坐标是(804,1),
故答案为:(804,1)
14.(2022秋·河北邯郸·八年级校考开学考试)如图,在平面直角坐标系中,有若干个整数点,其顺序按图中“”方向排列,如,,,,,,根据这个规律探索可得,第个点的坐标为______,第个点的坐标为______.
【思路点拨】
从图中可以看出横坐标为的有一个点,横坐标为的有个点,横坐标为的有个点,依此类推横坐标为的有个点.题目要求写出第个点和第个点的坐标,我们可以通过加法计算算出第个点和第个点分别位于第几列第几行,然后对应得出坐标规律,将行列数代入规律式.
【解题过程】
解:在横坐标上,第一列有一个点,第二列有个点第列有个点,
并且奇数列点数对称而偶数列点数轴上方比下方多一个,
,
第个点在第列自下而上第行,
所以奇数列的坐标为:;
偶数列的坐标为:.
由加法推算可得到第个点位于第列自下而上第行.
代入上式得第个点的坐标为,第个点的坐标为.
故答案为: .
15.(2022春·北京·七年级北京市第五中学分校校考期末)如图,在平面直角坐标系中,点.点第1次向上跳动1个单位至点,紧接着第2次向左跳动2个单位至点,第3次向上跳动1个单位至点,第4次向右跳动3个单位至点,第5次又向上跳动1个单位至点,第6次向左跳动4个单位至点,…照此规律,点第2022次跳动至点的坐标是________.
【思路点拨】
设第n次跳动至点,根据部分点的坐标找出变化规律“,,,”,照此规律由2022=4×505+2代入求解即可.
【解题过程】
解:设第n次跳动至点,
由图知,、、、、、、、、…,
∴可得:点的变化规律为,,,,
∵2022=4×505+2,
∴,即,
故答案为:.
16.(2022春·山东青岛·八年级校考期中)如图所示,一个机器人从O点出发,向正东方向走到达点,再向正北方向走到达点,再向正西方向走到达点,再向正南方向走到达点,再向正东方向走到达点,按照此规律走下去,相对于点O,机器人走到时,点的坐标是______,点的坐标是______.
【思路点拨】
根据题意求出点的坐标为;点的坐标为;点的坐标为;点的坐标为;点的坐标为;点的坐标为,依此类推,从点开始,每走动4次一个循环,从而得到点位于第一象限内,再由落在第一象限内的点每个循环,横坐标增加6,纵坐标增加6,即可求解.
【解题过程】
解:根据题意可知:,
∴点的坐标为;
点的坐标为,即;
点的坐标为,即;
点的坐标为,即;
点的坐标为,即;
依此类推,可得点的坐标为,即.
由此发现,从点开始,每走动4次一个循环,
∵,
∴点位于第一象限内,
∵点的坐标为,点的坐标为,点的坐标为,
∴落在第一象限内的点每个循环,横坐标增加6,纵坐标增加6,
∴点的坐标为,即.
故答案为①,②.
17.(2022秋·全国·八年级专题练习)如图,在平面直角坐标系中,有若干个整数点.其顺序按照图中“→”方向排列,即,,,,,…….根据这个规律,探究可得到第110个点的坐标为______.
【思路点拨】
观察点的坐标特点寻找规律,找到横坐标和纵坐标的变化特点即可解答.
【解题过程】
解:横坐标为1的点有1个,纵坐标为0;
横坐标为2的点有2个,纵坐标为0,1;
横坐标为3的点有3个,纵坐标为0,1,2;
横坐标为4的点有4个,纵坐标为0,1,2,3;
…,
发现规律:
因为1+2+3+4+…+14=105,
因为在第14行点的走向为向上,
所以第105个点的坐标为(14,13),
因为第15行点的走向为向下,
故第110个点在此行上,
横坐标为15,纵坐标为从106个点(15,14)向下数5个点,即为10;
故第110个点的坐标为(15,10)
故答案为:(15,10).
18.(2023秋·湖北孝感·九年级校考期末)如图,在平面直角坐标系中,有若干个横纵坐标分别为整数的点,其顺序为,,,,,,…,根据这个规律,第25个点的坐标为________,第2022个点的坐标为________.
【思路点拨】
观察图形可知,以最外边的矩形边长上的点为准,点的总个数等于轴上右下角的点的横坐标的平方,并且右下角的点的横坐标是奇数时最后以横坐标为该数,纵坐标为0结束,当右下角的点横坐标是偶数时,以横坐标为1,纵坐标为右下角横坐标的偶数减1的点结束,根据此规律解答即可.
【解题过程】
解:根据图形,以最外边的矩形边长上的点为准,点的总个数等于轴上右下角的点的横坐标的平方,
例如:右下角的点的横坐标为1,共有1个,,
右下角的点的横坐标为2时,共有4个,,
右下角的点的横坐标为3时,共有9个,,
右下角的点的横坐标为4时,共有16个,,
…
右下角的点的横坐标为时,共有个,
①∵,是奇数,
∴第25个点是,
②∵,是奇数,
∴第个点是,
即第个点是
故答案为,.
19.(2022春·河北邢台·七年级校考期末)如图,在平面直角坐标系中,轴,轴,点,,,在轴上,,,,,.
(1)若点在线段上,当点与点的距离最小时,点的坐标为____;
(2)把一条长为2022个单位长度且无弹性的细线(粗细忽略不计)的一端固定在处,并按的规律紧绕在图形“凸”的边上,则细线的另一端所在位置的点的坐标为____.
【思路点拨】
(1)根据两点之间线段最短即可求出答案;
(2)计算“凸”形图中各线段的长度,绕一周需要多少个单位长度,因为是周期变化,所以计算出绕了多少周,余下的线段落在哪里即可求出答案.
【解题过程】
(1)解:根据题意,画图如下,
∵两点之间线段最短,
∴当点 在的直线上时,点与点的距离最小,且点在线段 上,
∴点的坐标是 ,
故答案是:.
(2)解:∵,,,,,
从点的线段之和为 ,即,
∴ ,即绕了 周余下 个单位长度,也就是落在点 ,
∴细线的另一端所在位置的点的坐标是,
故答案是:.
20.(2022秋·全国·八年级专题练习)小明在学面直角坐标系后,突发奇想,画出了这样的图形(如图).他把图形与x轴正半轴的交点依次记作,,…,,图形与y轴正半轴的交点依次记作,,…,,图形与x轴负半轴的交点依次记作,,…,,图形与y轴负半轴的交点依次记作,,…,,发现其中包含了一定的数学规律.
请根据你发现的规律完成下列题目:
(1)请分别写出下列点的坐标:__________,__________,__________,__________.
(2)请分别写出下列点的坐标:__________,__________,__________,__________.
(3)请求出四边形的面积.
【思路点拨】
(1)根据点的坐标规律即可写出.
(2)根据点的坐标规律即可写出.
(3)四边形的面积为计算即可.
【解题过程】
由题意得:
的横坐标为,纵坐标为0,得出
的横坐标为0,纵坐标为,得出
的横坐标为 ,纵坐标为0,得出
的横坐标为0,纵坐标为,得出
故答案为:,,,
(2)根据上式得出的规律,直接即可写出,,,
故答案为:,,,
(3)∵,,,,
∴四边形的面积为
【典例1】综合与实践:
(1)动手探索在平面直角坐标系内,已知点,,,,连接,,,,,并依次取,,,,的中点,,,,,分别写出,,,的坐标;
(2)观察归纳以上各线段两端点的横、纵坐标与该线段中点的横、纵坐标之间的对应关系,猜想:若线段两端点坐标分别为、,线段的中点是,请用等式表示你所观察的规律 ,并用,的坐标验证规律是否正确 (填“是”或“否” ;
(3)实践运用利用上面探索得到的规律解决问题:
①若点,点,则线段的中点的坐标为 ;
②已知点是线段的中点,且点,,求点的坐标.
【思路点拨】
(1)根据图形可以直接读取坐标即可得到答案;
(2)根据观察得到规律并写出等式,再利用B、C、D、G、I五点坐标即可验证所得规律,得到答案;
(3)①根据(2)中发现的规律,即可得到线段的中点的坐标;
②设点的坐标为,根据根据(2)中发现的规律解方程求解即可得到点的坐标.
【解题过程】
(1)解:根据图形可以直接读取各点坐标,,,,,,
,,,的坐标分别为:,,,;
(2)解:根据各点坐标可以发现,线段中点坐标的纵坐标值为线段两端点纵坐标和的一半,线段中点坐标的横坐标值为线段两端点横坐标和的一半,
、,线段的中点是,
,
,,,,,、分别为线段、的中点,
检验得,,,
通过,的坐标验证规律是正确的,
故答案为:;是;
(3)解:①点,点,
根据(2)中发现的规律,线段的中点的坐标为,
故答案为:;
②设点的坐标为,
点是线段的中点,且点,,
,
,
点的坐标为.
1.(2023春·全国·七年级专题练习)如图,正方形的边长依次为2,4,6,8,……,他们在直角坐标系中的位置如图所示,其中,,,,,,,,,,……,按此规律接下去,则的坐标为( )
A. B.
C. D.
2.(2023·全国·七年级专题练习)如图,在一张无穷大的格纸上,格点的位置可用数对表示,如点的位置为,点的位置为.点从开始移动,规律为:第1次向右移动1个单位到,第2次向上移动2个单位到,第3次向右移动3个单位到,…,第次移动个单位(为奇数时向右,为偶数时向上),那么点第次移动到的位置为( )
A. B. C. D.
3.(2023秋·江苏扬州·八年级统考期末)如图,平面直角坐标系内,动点P第1次从点运动到点,第2次运动到点,第3次运动到点,……按这样的规律,第2023次运动到点的坐标是( )
A. B. C. D.
4.(2023春·全国·七年级专题练习)如图,在平面直角坐标系中,,,,,把一条长为2015个单位长度且没有弹性的细线(线的粗细忽略不计)的一端固定在点A处,并按…的规律紧绕在四边形的边上,则细线另一端所在位置的点的坐标是( )
A. B. C. D.
5.(2022春·河北廊坊·七年级校考阶段练习)如图,在平面直角坐标系中,动点从点出发,由跳动至点,依次跳动至点,点,点…根据这个规律,则点的坐标是( )
A.(1348,-1) B.(1348,2) C.(674,-1) D.(674,2)
6.(2023春·全国·七年级专题练习)如图,在平面直角坐标系上有点,点A第一次跳动至点,第二次点跳动至点,第三次点跳动至点,第四次点跳动至点,……依此规律跳动下去,则点与点之间的距离是( )
A.2023 B.2022 C.2021 D.2020
7.(2022秋·江苏·八年级专题练习)如图,在平面直角坐标系内原点O(0,0)第一次跳动到点A1(0,1),第二次从点A1跳动到点A2(1,2),第三次从点A2跳动到点A3(-1,3),第四次从点A3跳动到点A4(-1,4),……,按此规律下去,则点A2021的坐标是( ).
A.(673,2021) B.(674,2021) C.(-673,2021) D.(-674,2021)
8.(2022春·山东济宁·七年级统考期中)在平面直角坐标系中,一只小蛤蟆从原点O出发,第一次向上蹦到,第二次向右蹦到,第三次向下蹦到,第四次向右蹦到,第五次向上蹦到,…,按照此规律依次不间断蹦,每次蹦1个单位,其蹦的路线如图所示.那么按照上述规律,点的坐标是( )
A. B. C. D.
9.(2022·全国·七年级假期作业)如图所示,在平面直角坐标系中,将点A(-1,0)做如下的连续平移,A(-1,0)→A1(-1,1)→A2(2,1)→A3(2,-4)→A4(-5,-4)→A5(-5,5)…,按此规律平移下去,则A102的点坐标是( )
A. B. C. D.
10.(2023秋·山东东营·七年级统考期末)如图,已知A1(1,2),A2(2,2),A3(3,0),A4(4,﹣2),A5(5,﹣2),A6(6,0),…,按这样的规律,则点A2022的坐标为______.
11.(2023·全国·九年级专题练习)如图,动点P在平面直角坐标系中按图中箭头所示方向运动,第1次从原点运动到点,第2次接着运动到点,第3次接着运动到点,按这样的运动规律,经过第2017次运动后,动点P的坐标是______,经过第2018次运动后,动点P的坐标是______.
12.(2022秋·浙江·八年级专题练习)如图,已知点的坐标是,线段从原点出发后,在第一象限内按如下有规律的方式前行:,;,;,;…;则点的坐标是______.
13.(2023春·七年级单元测试)如图,在平面直角坐标系中,点A从依次跳动到,,,,,,,,,,…,按此规律,则点的坐标是______________
14.(2022秋·河北邯郸·八年级校考开学考试)如图,在平面直角坐标系中,有若干个整数点,其顺序按图中“”方向排列,如,,,,,,根据这个规律探索可得,第个点的坐标为______,第个点的坐标为______.
15.(2022春·北京·七年级北京市第五中学分校校考期末)如图,在平面直角坐标系中,点.点第1次向上跳动1个单位至点,紧接着第2次向左跳动2个单位至点,第3次向上跳动1个单位至点,第4次向右跳动3个单位至点,第5次又向上跳动1个单位至点,第6次向左跳动4个单位至点,…照此规律,点第2022次跳动至点的坐标是________.
16.(2022春·山东青岛·八年级校考期中)如图所示,一个机器人从O点出发,向正东方向走到达点,再向正北方向走到达点,再向正西方向走到达点,再向正南方向走到达点,再向正东方向走到达点,按照此规律走下去,相对于点O,机器人走到时,点的坐标是______,点的坐标是______.
17.(2022秋·全国·八年级专题练习)如图,在平面直角坐标系中,有若干个整数点.其顺序按照图中“→”方向排列,即,,,,,…….根据这个规律,探究可得到第110个点的坐标为______.
18.(2023秋·湖北孝感·九年级校考期末)如图,在平面直角坐标系中,有若干个横纵坐标分别为整数的点,其顺序为,,,,,,…,根据这个规律,第25个点的坐标为________,第2022个点的坐标为________.
19.(2022春·河北邢台·七年级校考期末)如图,在平面直角坐标系中,轴,轴,点,,,在轴上,,,,,.
(1)若点在线段上,当点与点的距离最小时,点的坐标为____;
(2)把一条长为2022个单位长度且无弹性的细线(粗细忽略不计)的一端固定在处,并按的规律紧绕在图形“凸”的边上,则细线的另一端所在位置的点的坐标为____.
20.(2022秋·全国·八年级专题练习)小明在学面直角坐标系后,突发奇想,画出了这样的图形(如图).他把图形与x轴正半轴的交点依次记作,,…,,图形与y轴正半轴的交点依次记作,,…,,图形与x轴负半轴的交点依次记作,,…,,图形与y轴负半轴的交点依次记作,,…,,发现其中包含了一定的数学规律.
请根据你发现的规律完成下列题目:
(1)请分别写出下列点的坐标:__________,__________,__________,__________.
(2)请分别写出下列点的坐标:__________,__________,__________,__________.
(3)请求出四边形的面积.
专题7.1 平面直角坐标系中的规律问题
【典例1】综合与实践:
(1)动手探索在平面直角坐标系内,已知点,,,,连接,,,,,并依次取,,,,的中点,,,,,分别写出,,,的坐标;
(2)观察归纳以上各线段两端点的横、纵坐标与该线段中点的横、纵坐标之间的对应关系,猜想:若线段两端点坐标分别为、,线段的中点是,请用等式表示你所观察的规律 ,并用,的坐标验证规律是否正确 (填“是”或“否” ;
(3)实践运用利用上面探索得到的规律解决问题:
①若点,点,则线段的中点的坐标为 ;
②已知点是线段的中点,且点,,求点的坐标.
【思路点拨】
(1)根据图形可以直接读取坐标即可得到答案;
(2)根据观察得到规律并写出等式,再利用B、C、D、G、I五点坐标即可验证所得规律,得到答案;
(3)①根据(2)中发现的规律,即可得到线段的中点的坐标;
②设点的坐标为,根据根据(2)中发现的规律解方程求解即可得到点的坐标.
【解题过程】
(1)解:根据图形可以直接读取各点坐标,,,,,,
,,,的坐标分别为:,,,;
(2)解:根据各点坐标可以发现,线段中点坐标的纵坐标值为线段两端点纵坐标和的一半,线段中点坐标的横坐标值为线段两端点横坐标和的一半,
、,线段的中点是,
,
,,,,,、分别为线段、的中点,
检验得,,,
通过,的坐标验证规律是正确的,
故答案为:;是;
(3)解:①点,点,
根据(2)中发现的规律,线段的中点的坐标为,
故答案为:;
②设点的坐标为,
点是线段的中点,且点,,
,
,
点的坐标为.
1.(2023春·全国·七年级专题练习)如图,正方形的边长依次为2,4,6,8,……,他们在直角坐标系中的位置如图所示,其中,,,,,,,,,,……,按此规律接下去,则的坐标为( )
A. B.
C. D.
【思路点拨】
由正方形的中心都是位于原点,边长依次为2,4,6,8,,可得第个正方形的顶点横坐标与纵坐标的绝对值都是.计算,根据商和余数知道是第几个正方形的顶点,且在哪一个象限,进而得出的坐标.
【解题过程】
解:,
顶点是第504个正方形的顶点,且在第四象限,
横坐标是,纵坐标是,
,
故选:B.
2.(2023·全国·七年级专题练习)如图,在一张无穷大的格纸上,格点的位置可用数对表示,如点的位置为,点的位置为.点从开始移动,规律为:第1次向右移动1个单位到,第2次向上移动2个单位到,第3次向右移动3个单位到,…,第次移动个单位(为奇数时向右,为偶数时向上),那么点第次移动到的位置为( )
A. B. C. D.
【思路点拨】
数对表示位置的方法是:第一个表示列,第二个表示行,当向右移动时,列的数字发生变化,行的数字不变,向上移动时,行的数字发生变化,列的数字不变,据此即可得解.
【解题过程】
解:根据题意可知:当向右移动时,列的数字发生变化,行的数字不变,当向上移动时,行的数字发生变化,列的数字不变,
∴点第次移动到的位置时,列的数字是中所有奇数的和,行的数字是中所有偶数的和,
∴,,
∴点第次移动到的位置为,
故选:.
3.(2023秋·江苏扬州·八年级统考期末)如图,平面直角坐标系内,动点P第1次从点运动到点,第2次运动到点,第3次运动到点,……按这样的规律,第2023次运动到点的坐标是( )
A. B. C. D.
【思路点拨】
根据图象可得出:横坐标为运动次数,纵坐标依次为4,2,1,,2,4,每5次一轮,进而即可求出答案.
【解题过程】
解:根据动点在平面直角坐标系中的运动,
,,,,,,
…,
∴横坐标为运动次数,经过第2023次运动后,点的横坐标是2020,
纵坐标依次为4,2,1,,2,每5次一轮,
∴ 4,
∴经过第2023次运动后,点的坐标是,
故选:C.
4.(2023春·全国·七年级专题练习)如图,在平面直角坐标系中,,,,,把一条长为2015个单位长度且没有弹性的细线(线的粗细忽略不计)的一端固定在点A处,并按…的规律紧绕在四边形的边上,则细线另一端所在位置的点的坐标是( )
A. B. C. D.
【思路点拨】
根据点的坐标求出四边形的周长,然后求出另一端是绕第几圈后的第几个单位长度,从而确定答案.
【解题过程】
解:∵,,,,
∴,,,,
∴绕四边形一周的细线长度为,
,
∴细线另一端在绕四边形第202圈的第5个单位长度的位置,即点C的位置,
∴点的坐标为.
故选:C.
5.(2022春·河北廊坊·七年级校考阶段练习)如图,在平面直角坐标系中,动点从点出发,由跳动至点,依次跳动至点,点,点…根据这个规律,则点的坐标是( )
A.(1348,-1) B.(1348,2) C.(674,-1) D.(674,2)
【思路点拨】
观察可知,,,,每三个点为一组,纵坐标为0,2,-1循环,每个循环内横坐标增加2,据此求解即可.
【解题过程】
解:∵动点从点出发,由跳动至点,依次跳动至点,点,点…
∴,,,,每三个点为一组,纵坐标为0,2,-1循环,每个循环内横坐标增加2,
∵,
∴点的纵坐标与点的纵坐标相同,即为-1,点横坐标为,
∴点的坐标为(1348,-1).
故选:A.
6.(2023春·全国·七年级专题练习)如图,在平面直角坐标系上有点,点A第一次跳动至点,第二次点跳动至点,第三次点跳动至点,第四次点跳动至点,……依此规律跳动下去,则点与点之间的距离是( )
A.2023 B.2022 C.2021 D.2020
【思路点拨】
根据图形观察发现,第偶数次跳动至点的坐标,横坐标是次数的一半加上1,纵坐标是次数的一半,奇数次跳动与该偶数次跳动的横坐标的相反数加上1,纵坐标相同,可分别求出点与点的坐标,进而可求出点与点之间的距离.
【解题过程】
解:观察发现,第2次跳动至点的坐标是,
第4次跳动至点的坐标是,
第6次跳动至点的坐标是,
第8次跳动至点的坐标是,
…
第2n次跳动至点的坐标是,
则第2022次跳动至点的坐标是,
第2021次跳动至点的坐标是.
∵点与点的纵坐标相等,
∴点与点之间的距离,
故选:A.
7.(2022秋·江苏·八年级专题练习)如图,在平面直角坐标系内原点O(0,0)第一次跳动到点A1(0,1),第二次从点A1跳动到点A2(1,2),第三次从点A2跳动到点A3(-1,3),第四次从点A3跳动到点A4(-1,4),……,按此规律下去,则点A2021的坐标是( ).
A.(673,2021) B.(674,2021) C.(-673,2021) D.(-674,2021)
【思路点拨】
根据已知点的坐标寻找规律并应用解答即可.
【解题过程】
解:∵A1(0,1),A2(1,2),A3(-1,3),A4(-1,4),
∴A5(2,5),A6(-2,6),A7(-2,7),A8(3,8),
∴A3n-1(n,3n-1),A3n(-n,3n),A3n+1(-n,3n+1)(n为正整数),
∵3×674-1=2021,
∴n=674,所以A 2021(674,2021).
故选B.
8.(2022春·山东济宁·七年级统考期中)在平面直角坐标系中,一只小蛤蟆从原点O出发,第一次向上蹦到,第二次向右蹦到,第三次向下蹦到,第四次向右蹦到,第五次向上蹦到,…,按照此规律依次不间断蹦,每次蹦1个单位,其蹦的路线如图所示.那么按照上述规律,点的坐标是( )
A. B. C. D.
【思路点拨】
根据图象可得移动4次图象完成一个循环,再由2022÷4=505……2,可得点A2022在第505个循环的第2个点的位置,即纵坐标与A1的相同,为1,再由A4(2,0),A8(4,0),A12(6,0),……,可得A4n(2n,0),从而得到A2020的坐标是(1010,0),从而可得出点A2022的坐标.
【解题过程】
解:根据题意得:点A1(0,1),A2(1,1),A3(1,0),A4(2,0),A5(2,1),……
∴每移动4次图象完成一个循环,
∵2022÷4=505……2,
∴点A2022在第505个循环的第2个点的位置,即纵坐标与A1的相同,为1,
∵A4(2,0),A8(4,0),A12(6,0),……,
∴A4n(2n,0),
∴A2020的坐标是(1010,0),
∴A2022的坐标是(1010+1,1),即A2022的坐标是(1011,1).
故选:D.
9.(2022·全国·七年级假期作业)如图所示,在平面直角坐标系中,将点A(-1,0)做如下的连续平移,A(-1,0)→A1(-1,1)→A2(2,1)→A3(2,-4)→A4(-5,-4)→A5(-5,5)…,按此规律平移下去,则A102的点坐标是( )
A. B. C. D.
【思路点拨】
根据题意可知,点A平移时每4次为一个周期,由102÷4=25 2,可知点A102的坐标与A4n+2的点的坐标规律相同,分别求出A2,A6,A10的坐标,找出规律,进而求解即可.
【解题过程】
解:由题意可知,将点A(-1,0)向上平移1个单位长度得到A1(-1,1),再向右平移3个单位长度得到A2(2,1),再向下平移5个单位长度得到A3(2,-4),再向左平移7个单位长度得到A4(-5,-4);再向上平移9个单位长度得到A5(-5,5)…,
∴点A平移时每4次为一个周期.
∵102÷4=25 2,
∴点A102的坐标与A4n+2的点的坐标规律相同.
∵A2(2,1),A6(6,5),A10(10,9),
以此类推,
∴A4n+2(4n+2,4n+1),
∴A102的点坐标是(102,101).
故选:C.
10.(2023秋·山东东营·七年级统考期末)如图,已知A1(1,2),A2(2,2),A3(3,0),A4(4,﹣2),A5(5,﹣2),A6(6,0),…,按这样的规律,则点A2022的坐标为______.
【思路点拨】
观察发现,每6个点形成一个循环,再根据点A6的坐标及2022÷6所得的整数及余数,可计算出点A2022的横坐标,再根据余数对比第一组的相应位置的数可得其纵坐标.
【解题过程】
解:观察发现,每6个点形成一个循环,
∵A6(6,0),
∴OA6=6,
∵2022÷6=337,
∴点A2022的位于第337个循环组的第6个,
∴点A2022的横坐标为6×337=2022,其纵坐标为:0,
∴点A2022的坐标为(2022,0).
故答案为:(2022,0).
11.(2023·全国·九年级专题练习)如图,动点P在平面直角坐标系中按图中箭头所示方向运动,第1次从原点运动到点,第2次接着运动到点,第3次接着运动到点,按这样的运动规律,经过第2017次运动后,动点P的坐标是______,经过第2018次运动后,动点P的坐标是______.
【思路点拨】
观察前几次运动后点的坐标,不难发现动点P的横坐标等于运动的次数,而纵坐标的变化为1,0,2,0,1,0,2,0…,4个一循环;
接下来通过总结得到的规律,再结合2017÷4=504……1,即可求出经过2017次运动后动点P的坐标了,同理可找到2018次运动后动点P的坐标.
【解题过程】
根据动点P在平面直角坐标系中按图中箭头所示方向运动,
第1次从原点运动到点(1,1),
第2次接着运动到点(2,0),
第3次接着运动到点(3,2),
第4次接着运动到点(4,0),
第5次接着运动到点(5,1),
…
∴横坐标为运动次数,经过第2017次运动后,动点P的横坐标为2017,纵坐标为1,0,2,0,每4次一轮,
∴经过第2017次运动后,动点P的纵坐标为:2017÷4=504……1,故纵坐标为四个数中第一个,即1,
∴经过第2017次运动后,动点P的坐标是(2017,1).
∵2018÷4=504……2,
∴经过第2018次运动后,动点P的坐标是(2018,0).
故答案为 , .
12.(2022秋·浙江·八年级专题练习)如图,已知点的坐标是,线段从原点出发后,在第一象限内按如下有规律的方式前行:,;,;,;…;则点的坐标是______.
【思路点拨】
先得出A1(1,2),A2(3,1),A3(4,3),A4(6,2),A5(7,4),A6(9,3)的坐标,观察可得A的纵坐标的规律,然后确定A的横坐标与下标之间的关系即可求解.
【解题过程】
解:A1(1,2),A2(3,1),A3(4,3),A4(6,2),A5(7,4),A6(9,3),…,
可得:
A1横坐标为:×3 2=1,纵坐标为:+1=2;
A3横坐标为:×3 2=4,纵坐标为:+1=3;
A5横坐标为:×3 2=7,纵坐标为:+1=4,…;
∴下标为奇数时,横坐标依次为:1,4,7,…,纵坐标为:2,3,4,…;
∴A2023横坐标为:×3 2=3034,纵坐标为:+1=1013…;
∴A2023的坐标为:(3034,1013),
故答案为:(3034,1013).
13.(2023春·七年级单元测试)如图,在平面直角坐标系中,点A从依次跳动到,,,,,,,,,,…,按此规律,则点的坐标是______________
【思路点拨】
根据图形可以发现规律,从到是一个循环,一个循环周期是10,一个循环后又回到x轴上,且一个循环后横坐标增加4个单位,先求出点的坐标(804,0),再求点的坐标即可.
【解题过程】
解:观察图形可知,n为正整数时,的纵坐标为0,1,3,﹣3
纵坐标为0的点:
纵坐标为1的点:
纵坐标为3的点:
纵坐标为﹣3的点:
可以看出纵坐标为1,3,﹣3时,n取连续的两个数为一组,则10个10个的增加,
∵2021=10×202+1,纵坐标为1的规律
∴的纵坐标为1,
由,解得n=203,
∵正好是往右循环203次,
∴横坐标为﹣4+(203-1)×4=804,
∴点的坐标是(804,1),
故答案为:(804,1)
14.(2022秋·河北邯郸·八年级校考开学考试)如图,在平面直角坐标系中,有若干个整数点,其顺序按图中“”方向排列,如,,,,,,根据这个规律探索可得,第个点的坐标为______,第个点的坐标为______.
【思路点拨】
从图中可以看出横坐标为的有一个点,横坐标为的有个点,横坐标为的有个点,依此类推横坐标为的有个点.题目要求写出第个点和第个点的坐标,我们可以通过加法计算算出第个点和第个点分别位于第几列第几行,然后对应得出坐标规律,将行列数代入规律式.
【解题过程】
解:在横坐标上,第一列有一个点,第二列有个点第列有个点,
并且奇数列点数对称而偶数列点数轴上方比下方多一个,
,
第个点在第列自下而上第行,
所以奇数列的坐标为:;
偶数列的坐标为:.
由加法推算可得到第个点位于第列自下而上第行.
代入上式得第个点的坐标为,第个点的坐标为.
故答案为: .
15.(2022春·北京·七年级北京市第五中学分校校考期末)如图,在平面直角坐标系中,点.点第1次向上跳动1个单位至点,紧接着第2次向左跳动2个单位至点,第3次向上跳动1个单位至点,第4次向右跳动3个单位至点,第5次又向上跳动1个单位至点,第6次向左跳动4个单位至点,…照此规律,点第2022次跳动至点的坐标是________.
【思路点拨】
设第n次跳动至点,根据部分点的坐标找出变化规律“,,,”,照此规律由2022=4×505+2代入求解即可.
【解题过程】
解:设第n次跳动至点,
由图知,、、、、、、、、…,
∴可得:点的变化规律为,,,,
∵2022=4×505+2,
∴,即,
故答案为:.
16.(2022春·山东青岛·八年级校考期中)如图所示,一个机器人从O点出发,向正东方向走到达点,再向正北方向走到达点,再向正西方向走到达点,再向正南方向走到达点,再向正东方向走到达点,按照此规律走下去,相对于点O,机器人走到时,点的坐标是______,点的坐标是______.
【思路点拨】
根据题意求出点的坐标为;点的坐标为;点的坐标为;点的坐标为;点的坐标为;点的坐标为,依此类推,从点开始,每走动4次一个循环,从而得到点位于第一象限内,再由落在第一象限内的点每个循环,横坐标增加6,纵坐标增加6,即可求解.
【解题过程】
解:根据题意可知:,
∴点的坐标为;
点的坐标为,即;
点的坐标为,即;
点的坐标为,即;
点的坐标为,即;
依此类推,可得点的坐标为,即.
由此发现,从点开始,每走动4次一个循环,
∵,
∴点位于第一象限内,
∵点的坐标为,点的坐标为,点的坐标为,
∴落在第一象限内的点每个循环,横坐标增加6,纵坐标增加6,
∴点的坐标为,即.
故答案为①,②.
17.(2022秋·全国·八年级专题练习)如图,在平面直角坐标系中,有若干个整数点.其顺序按照图中“→”方向排列,即,,,,,…….根据这个规律,探究可得到第110个点的坐标为______.
【思路点拨】
观察点的坐标特点寻找规律,找到横坐标和纵坐标的变化特点即可解答.
【解题过程】
解:横坐标为1的点有1个,纵坐标为0;
横坐标为2的点有2个,纵坐标为0,1;
横坐标为3的点有3个,纵坐标为0,1,2;
横坐标为4的点有4个,纵坐标为0,1,2,3;
…,
发现规律:
因为1+2+3+4+…+14=105,
因为在第14行点的走向为向上,
所以第105个点的坐标为(14,13),
因为第15行点的走向为向下,
故第110个点在此行上,
横坐标为15,纵坐标为从106个点(15,14)向下数5个点,即为10;
故第110个点的坐标为(15,10)
故答案为:(15,10).
18.(2023秋·湖北孝感·九年级校考期末)如图,在平面直角坐标系中,有若干个横纵坐标分别为整数的点,其顺序为,,,,,,…,根据这个规律,第25个点的坐标为________,第2022个点的坐标为________.
【思路点拨】
观察图形可知,以最外边的矩形边长上的点为准,点的总个数等于轴上右下角的点的横坐标的平方,并且右下角的点的横坐标是奇数时最后以横坐标为该数,纵坐标为0结束,当右下角的点横坐标是偶数时,以横坐标为1,纵坐标为右下角横坐标的偶数减1的点结束,根据此规律解答即可.
【解题过程】
解:根据图形,以最外边的矩形边长上的点为准,点的总个数等于轴上右下角的点的横坐标的平方,
例如:右下角的点的横坐标为1,共有1个,,
右下角的点的横坐标为2时,共有4个,,
右下角的点的横坐标为3时,共有9个,,
右下角的点的横坐标为4时,共有16个,,
…
右下角的点的横坐标为时,共有个,
①∵,是奇数,
∴第25个点是,
②∵,是奇数,
∴第个点是,
即第个点是
故答案为,.
19.(2022春·河北邢台·七年级校考期末)如图,在平面直角坐标系中,轴,轴,点,,,在轴上,,,,,.
(1)若点在线段上,当点与点的距离最小时,点的坐标为____;
(2)把一条长为2022个单位长度且无弹性的细线(粗细忽略不计)的一端固定在处,并按的规律紧绕在图形“凸”的边上,则细线的另一端所在位置的点的坐标为____.
【思路点拨】
(1)根据两点之间线段最短即可求出答案;
(2)计算“凸”形图中各线段的长度,绕一周需要多少个单位长度,因为是周期变化,所以计算出绕了多少周,余下的线段落在哪里即可求出答案.
【解题过程】
(1)解:根据题意,画图如下,
∵两点之间线段最短,
∴当点 在的直线上时,点与点的距离最小,且点在线段 上,
∴点的坐标是 ,
故答案是:.
(2)解:∵,,,,,
从点的线段之和为 ,即,
∴ ,即绕了 周余下 个单位长度,也就是落在点 ,
∴细线的另一端所在位置的点的坐标是,
故答案是:.
20.(2022秋·全国·八年级专题练习)小明在学面直角坐标系后,突发奇想,画出了这样的图形(如图).他把图形与x轴正半轴的交点依次记作,,…,,图形与y轴正半轴的交点依次记作,,…,,图形与x轴负半轴的交点依次记作,,…,,图形与y轴负半轴的交点依次记作,,…,,发现其中包含了一定的数学规律.
请根据你发现的规律完成下列题目:
(1)请分别写出下列点的坐标:__________,__________,__________,__________.
(2)请分别写出下列点的坐标:__________,__________,__________,__________.
(3)请求出四边形的面积.
【思路点拨】
(1)根据点的坐标规律即可写出.
(2)根据点的坐标规律即可写出.
(3)四边形的面积为计算即可.
【解题过程】
由题意得:
的横坐标为,纵坐标为0,得出
的横坐标为0,纵坐标为,得出
的横坐标为 ,纵坐标为0,得出
的横坐标为0,纵坐标为,得出
故答案为:,,,
(2)根据上式得出的规律,直接即可写出,,,
故答案为:,,,
(3)∵,,,,
∴四边形的面积为
