(人教A版2019选择性必修第二册)高二数学5.1导数的概念及意义(精讲)(含解析)
文档属性
| 名称 | (人教A版2019选择性必修第二册)高二数学5.1导数的概念及意义(精讲)(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 979.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-27 21:43:26 | ||
图片预览




文档简介
5.1 导数的概念及意义(精讲)
考点一 平均速度
【例1】(2021·江苏省灌南高级中学)已知函数,则该函数在区间上的平均变化率为( )
A. B. C. D.
【一隅三反】
1(2022·浙江·高二期中)函数在区间上的平均变化率等于( )
A. B.1 C.2 D.
2.(2022·陕西)一个物体做直线运动,位移(单位:)与时间(单位:)之间的函数关系为,且这一物体在这段时间内的平均速度为,则实数的值为( )
A.2 B.1 C. D.
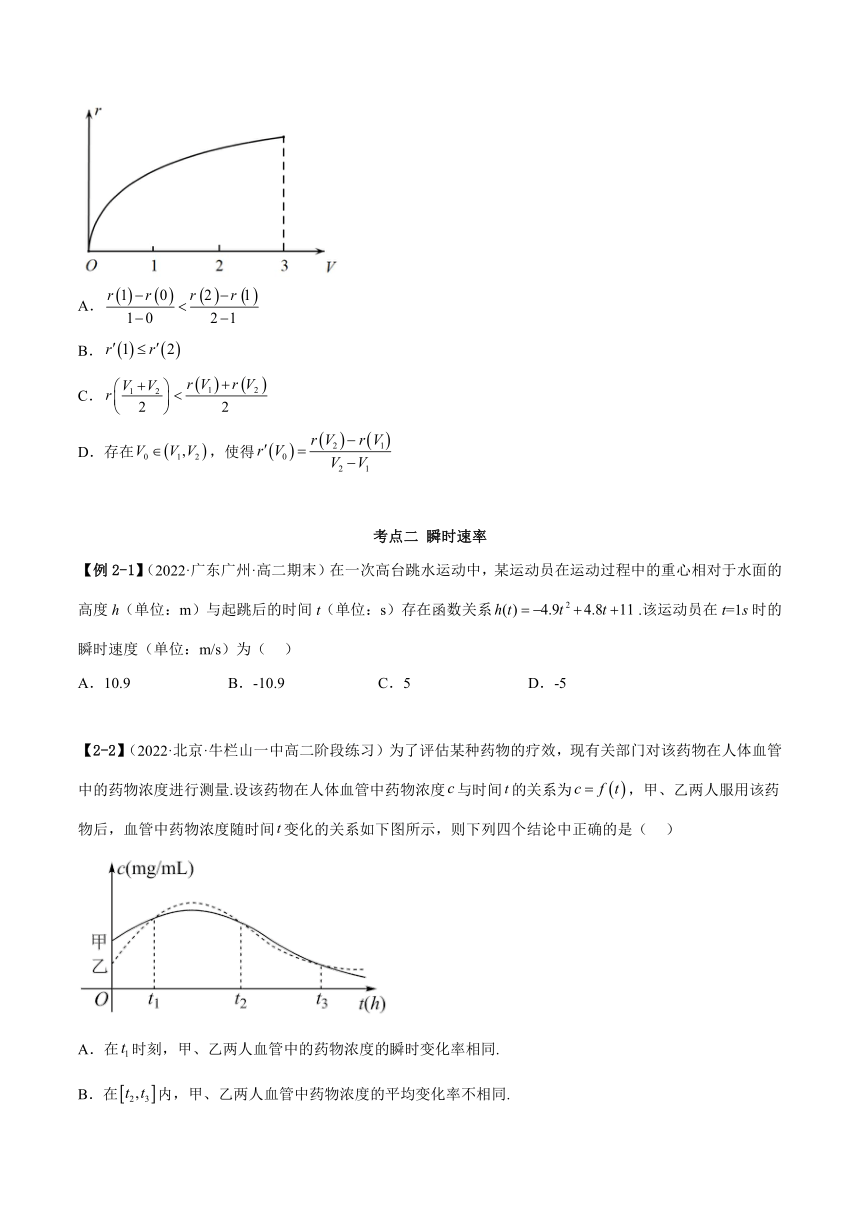
3.(2022·四川·成都七中高二期末(文))吹气球时,记气球的半径r与体积V之间的函数关系为,为的导函数.已知在上的图像如图所示,若,则下列结论正确的是( )
A.
B.
C.
D.存在,使得
考点二 瞬时速率
【例2-1】(2022·广东广州·高二期末)在一次高台跳水运动中,某运动员在运动过程中的重心相对于水面的高度h(单位:m)与起跳后的时间t(单位:s)存在函数关系.该运动员在t=1s时的瞬时速度(单位:m/s)为( )
A.10.9 B.-10.9 C.5 D.-5
【2-2】(2022·北京·牛栏山一中高二阶段练习)为了评估某种药物的疗效,现有关部门对该药物在人体血管中的药物浓度进行测量.设该药物在人体血管中药物浓度与时间的关系为,甲、乙两人服用该药物后,血管中药物浓度随时间变化的关系如下图所示,则下列四个结论中正确的是( )
A.在时刻,甲、乙两人血管中的药物浓度的瞬时变化率相同.
B.在内,甲、乙两人血管中药物浓度的平均变化率不相同.
C.若,则在时刻,甲、乙两人血管中药物浓度的瞬时变化率一定不同
D.若,则在时刻,甲血管中药物浓度不高于乙血管中药物浓度
【一隅三反】
1.(2022·北京市育英学校高二期中)已知某物体运动的位移关于时间的函数为,则当时的瞬时速度是( )
A.5m/s B.4m/s C.3m/s D.2m/s
2.(2022·全国·高二课时练习)某物体的运动路程s(单位:m)与时间t(单位:s)的关系可用函数表示,则物体在t=0 s时的瞬时速度为______m/s;瞬时速度为9 m/s的时刻是在t=______s时.
3.(2022·北京通州·高二期中)假设某高山滑雪运动员在一次高山滑雪训练中滑行的路程l(单位:m)与时间t(单位:s)之间的函数关系为,则该运动员在这段时间的平均速度为______m/s;在时的瞬时速度为______m/s.
考点三 某处导数
【例3-1】(2022·广东·南海中学高二期中)设,则( )
A. B. C.4 D.8
【例3-2】.(2022·山东·文登新一中高二期中)设存在导函数且满足,则曲线上的点处的切线的斜率为( )
A. B. C.1 D.2
【一隅三反】
1.(2022·全国·高三专题练习)若函数在处的导数为2,则 ( )
A.2 B.1 C. D.6
2.(2022·天津市武清区杨村第一中学高二阶段练习)设函数,则( )
A.1 B.5 C. D.0
3.(2022·全国·高二课时练习)已知函数的导函数为,且,则实数的值为( )
A. B. C. D.
考点四 导数的几何意义及应用
【例4-1】(2021·江苏·南京市中华中学高二期中)已如函数在处的切线斜率为2,则 等于( )
A.2 B.1 C.4 D.12
【例4-2】(2021·全国·高二课时练习)函数的图象在点处的切线的倾斜角的大小为______.
【一隅三反】
1.(2021·全国·高二课前预习)抛物线y=x2+1在点(1,2)处的切线的斜率是________.
2.(2022·全国高二课时练习)曲线y=x+上任意一点P处的切线斜率为k,则k的取值范围是
3.(2022广东)曲线y=x2-2在点x=1处的切线的倾斜角为( )
A.30° B.45° C.135° D.165°
4.(2022·全国·高二课时练习)(多选)若当,满足,则下列结论正确的是( )
A.
B.
C.曲线上点处的切线斜率为
D.曲线上点处的切线斜率为
5.1 导数的概念及意义(精讲)
考点一 平均速度
【例1】(2021·江苏省灌南高级中学)已知函数,则该函数在区间上的平均变化率为( )
A. B. C. D.
答案:A
【解析】因为函数,所以该函数在区间上的平均变化率为
,故选:A
【一隅三反】
1(2022·浙江·高二期中)函数在区间上的平均变化率等于( )
A. B.1 C.2 D.
答案:C
【解析】因为,,
所以,即函数在区间上的平均变化率为;故选:C
2.(2022·陕西)一个物体做直线运动,位移(单位:)与时间(单位:)之间的函数关系为,且这一物体在这段时间内的平均速度为,则实数的值为( )
A.2 B.1 C. D.
答案:A
【解析】,,
因为物体在这段时间内的平均速度为,所以,解得,
故选:A
3.(2022·四川·成都七中高二期末(文))吹气球时,记气球的半径r与体积V之间的函数关系为,为的导函数.已知在上的图像如图所示,若,则下列结论正确的是( )
A.
B.
C.
D.存在,使得
答案:D
【解析】A:设,由图得,
所以所以,所以该选项错误;
B:由图得图像上点的切线的斜率越来越小,根据导数的几何意义得,所以该选项错误;
C:设,因为
所以,所以该选项错误;
D:表示两点之间的斜率,表示处切线的斜率,由于,所以可以平移直线使之和曲线相切,切点就是点,所以该选项正确.故选:D
考点二 瞬时速率
【例2-1】(2022·广东广州·高二期末)在一次高台跳水运动中,某运动员在运动过程中的重心相对于水面的高度h(单位:m)与起跳后的时间t(单位:s)存在函数关系.该运动员在t=1s时的瞬时速度(单位:m/s)为( )
A.10.9 B.-10.9 C.5 D.-5
答案:D
【解析】因为,所以,令,得瞬时速度为.故选:D.
【2-2】(2022·北京·牛栏山一中高二阶段练习)为了评估某种药物的疗效,现有关部门对该药物在人体血管中的药物浓度进行测量.设该药物在人体血管中药物浓度与时间的关系为,甲、乙两人服用该药物后,血管中药物浓度随时间变化的关系如下图所示,则下列四个结论中正确的是( )
A.在时刻,甲、乙两人血管中的药物浓度的瞬时变化率相同.
B.在内,甲、乙两人血管中药物浓度的平均变化率不相同.
C.若,则在时刻,甲、乙两人血管中药物浓度的瞬时变化率一定不同
D.若,则在时刻,甲血管中药物浓度不高于乙血管中药物浓度
答案:D
【解析】对于A选项,在时刻,两曲线交于同一点,说明甲、乙两人血管中的药物浓度相同,瞬时变化率为切线的斜率,故不相同,故A错误;
对于B选项,在两个时刻,甲、乙两人血管中药物浓度相同,因此在这个时间段内,甲、乙两人血管中药物浓度的平均变化率相同,故B错误;
对于C选项, 这个时间段内,在时刻时,甲血管中药物浓度的瞬时变化率大于乙血管中药物浓度的瞬时变化率,在时刻时,甲血管中药物浓度的瞬时变化率小于乙血管中药物浓度的瞬时变化率,故存在使得甲、乙两人血管中药物浓度的瞬时变化率相同,故C错误;
对于D选项,在内,乙血管中药物浓度始终大于甲血管中药物浓度,在时刻,甲乙血管中药物浓度相同,故若,则在时刻,甲血管中药物浓度不高于乙血管中药物浓度,D正确.故选:D.
【一隅三反】
1.(2022·北京市育英学校高二期中)已知某物体运动的位移关于时间的函数为,则当时的瞬时速度是( )
A.5m/s B.4m/s C.3m/s D.2m/s
答案:A
【解析】因为,所以当时的瞬时速度是.故选:A
2.(2022·全国·高二课时练习)某物体的运动路程s(单位:m)与时间t(单位:s)的关系可用函数表示,则物体在t=0 s时的瞬时速度为______m/s;瞬时速度为9 m/s的时刻是在t=______s时.
答案: 1 4
【解析】,
即物体在t=0 s时的瞬时速度为1 m/s.设物体在时刻的瞬时速度为9 m/s,
又,
所以,物体在t=4 s时的瞬时速度为9 m/s.故答案为:1;4
3.(2022·北京通州·高二期中)假设某高山滑雪运动员在一次高山滑雪训练中滑行的路程l(单位:m)与时间t(单位:s)之间的函数关系为,则该运动员在这段时间的平均速度为______m/s;在时的瞬时速度为______m/s.
答案:
【解析】答题空1:该运动员在这段时间的平均速度为:
答题空2:由得,当时,.
故答案为:,
考点三 某处导数
【例3-1】(2022·广东·南海中学高二期中)设,则( )
A. B. C.4 D.8
答案:C
【解析】
故选:C
【例3-2】.(2022·山东·文登新一中高二期中)设存在导函数且满足,则曲线上的点处的切线的斜率为( )
A. B. C.1 D.2
答案:A
【解析】因为存在导函数且满足,
所以,即曲线上的点处的切线的斜率为,
故选:A.
【一隅三反】
1.(2022·全国·高三专题练习)若函数在处的导数为2,则 ( )
A.2 B.1 C. D.6
答案:B
【解析】由函数在处的导数为2,得,
所以,故选:B
2.(2022·天津市武清区杨村第一中学高二阶段练习)设函数,则( )
A.1 B.5 C. D.0
答案:B
【解析】由题意,所以,所以原式等于.
故选:B.
3.(2022·全国·高二课时练习)已知函数的导函数为,且,则实数的值为( )
A. B. C. D.
答案:D
【解析】,解得故选:D
考点四 导数的几何意义及应用
【例4-1】(2021·江苏·南京市中华中学高二期中)已如函数在处的切线斜率为2,则 等于( )
A.2 B.1 C.4 D.12
答案:C
【解析】函数在处的切线斜率为2,所以,
所以.故选:C
【例4-2】(2021·全国·高二课时练习)函数的图象在点处的切线的倾斜角的大小为______.
答案:135°
【解析】,即函数的图象在点处的切线的斜率为-1,所以切线的倾斜角.
故答案为:135°
【一隅三反】
1.(2021·全国·高二课前预习)抛物线y=x2+1在点(1,2)处的切线的斜率是________.
答案:2
【解析】k= = (2+Δx)=2.答案 2
2.(2022·全国高二课时练习)曲线y=x+上任意一点P处的切线斜率为k,则k的取值范围是
答案:(-∞,1)
【解析】上任意一点P(x0,y0)处的切线斜率为
== =<1,即k<1.
3.(2022广东)曲线y=x2-2在点x=1处的切线的倾斜角为( )
A.30° B.45° C.135° D.165°
答案:B
【解析】因为,故,故,
设曲线在处的切线的倾斜角为,则,而,故,故选:B.
4.(2022·全国·高二课时练习)(多选)若当,满足,则下列结论正确的是( )
A.
B.
C.曲线上点处的切线斜率为
D.曲线上点处的切线斜率为
答案:AD
【解析】由得:,即,
曲线上点处的切线斜率为,C错误;D正确;
,A正确;B错误.故选:AD.
考点一 平均速度
【例1】(2021·江苏省灌南高级中学)已知函数,则该函数在区间上的平均变化率为( )
A. B. C. D.
【一隅三反】
1(2022·浙江·高二期中)函数在区间上的平均变化率等于( )
A. B.1 C.2 D.
2.(2022·陕西)一个物体做直线运动,位移(单位:)与时间(单位:)之间的函数关系为,且这一物体在这段时间内的平均速度为,则实数的值为( )
A.2 B.1 C. D.
3.(2022·四川·成都七中高二期末(文))吹气球时,记气球的半径r与体积V之间的函数关系为,为的导函数.已知在上的图像如图所示,若,则下列结论正确的是( )
A.
B.
C.
D.存在,使得
考点二 瞬时速率
【例2-1】(2022·广东广州·高二期末)在一次高台跳水运动中,某运动员在运动过程中的重心相对于水面的高度h(单位:m)与起跳后的时间t(单位:s)存在函数关系.该运动员在t=1s时的瞬时速度(单位:m/s)为( )
A.10.9 B.-10.9 C.5 D.-5
【2-2】(2022·北京·牛栏山一中高二阶段练习)为了评估某种药物的疗效,现有关部门对该药物在人体血管中的药物浓度进行测量.设该药物在人体血管中药物浓度与时间的关系为,甲、乙两人服用该药物后,血管中药物浓度随时间变化的关系如下图所示,则下列四个结论中正确的是( )
A.在时刻,甲、乙两人血管中的药物浓度的瞬时变化率相同.
B.在内,甲、乙两人血管中药物浓度的平均变化率不相同.
C.若,则在时刻,甲、乙两人血管中药物浓度的瞬时变化率一定不同
D.若,则在时刻,甲血管中药物浓度不高于乙血管中药物浓度
【一隅三反】
1.(2022·北京市育英学校高二期中)已知某物体运动的位移关于时间的函数为,则当时的瞬时速度是( )
A.5m/s B.4m/s C.3m/s D.2m/s
2.(2022·全国·高二课时练习)某物体的运动路程s(单位:m)与时间t(单位:s)的关系可用函数表示,则物体在t=0 s时的瞬时速度为______m/s;瞬时速度为9 m/s的时刻是在t=______s时.
3.(2022·北京通州·高二期中)假设某高山滑雪运动员在一次高山滑雪训练中滑行的路程l(单位:m)与时间t(单位:s)之间的函数关系为,则该运动员在这段时间的平均速度为______m/s;在时的瞬时速度为______m/s.
考点三 某处导数
【例3-1】(2022·广东·南海中学高二期中)设,则( )
A. B. C.4 D.8
【例3-2】.(2022·山东·文登新一中高二期中)设存在导函数且满足,则曲线上的点处的切线的斜率为( )
A. B. C.1 D.2
【一隅三反】
1.(2022·全国·高三专题练习)若函数在处的导数为2,则 ( )
A.2 B.1 C. D.6
2.(2022·天津市武清区杨村第一中学高二阶段练习)设函数,则( )
A.1 B.5 C. D.0
3.(2022·全国·高二课时练习)已知函数的导函数为,且,则实数的值为( )
A. B. C. D.
考点四 导数的几何意义及应用
【例4-1】(2021·江苏·南京市中华中学高二期中)已如函数在处的切线斜率为2,则 等于( )
A.2 B.1 C.4 D.12
【例4-2】(2021·全国·高二课时练习)函数的图象在点处的切线的倾斜角的大小为______.
【一隅三反】
1.(2021·全国·高二课前预习)抛物线y=x2+1在点(1,2)处的切线的斜率是________.
2.(2022·全国高二课时练习)曲线y=x+上任意一点P处的切线斜率为k,则k的取值范围是
3.(2022广东)曲线y=x2-2在点x=1处的切线的倾斜角为( )
A.30° B.45° C.135° D.165°
4.(2022·全国·高二课时练习)(多选)若当,满足,则下列结论正确的是( )
A.
B.
C.曲线上点处的切线斜率为
D.曲线上点处的切线斜率为
5.1 导数的概念及意义(精讲)
考点一 平均速度
【例1】(2021·江苏省灌南高级中学)已知函数,则该函数在区间上的平均变化率为( )
A. B. C. D.
答案:A
【解析】因为函数,所以该函数在区间上的平均变化率为
,故选:A
【一隅三反】
1(2022·浙江·高二期中)函数在区间上的平均变化率等于( )
A. B.1 C.2 D.
答案:C
【解析】因为,,
所以,即函数在区间上的平均变化率为;故选:C
2.(2022·陕西)一个物体做直线运动,位移(单位:)与时间(单位:)之间的函数关系为,且这一物体在这段时间内的平均速度为,则实数的值为( )
A.2 B.1 C. D.
答案:A
【解析】,,
因为物体在这段时间内的平均速度为,所以,解得,
故选:A
3.(2022·四川·成都七中高二期末(文))吹气球时,记气球的半径r与体积V之间的函数关系为,为的导函数.已知在上的图像如图所示,若,则下列结论正确的是( )
A.
B.
C.
D.存在,使得
答案:D
【解析】A:设,由图得,
所以所以,所以该选项错误;
B:由图得图像上点的切线的斜率越来越小,根据导数的几何意义得,所以该选项错误;
C:设,因为
所以,所以该选项错误;
D:表示两点之间的斜率,表示处切线的斜率,由于,所以可以平移直线使之和曲线相切,切点就是点,所以该选项正确.故选:D
考点二 瞬时速率
【例2-1】(2022·广东广州·高二期末)在一次高台跳水运动中,某运动员在运动过程中的重心相对于水面的高度h(单位:m)与起跳后的时间t(单位:s)存在函数关系.该运动员在t=1s时的瞬时速度(单位:m/s)为( )
A.10.9 B.-10.9 C.5 D.-5
答案:D
【解析】因为,所以,令,得瞬时速度为.故选:D.
【2-2】(2022·北京·牛栏山一中高二阶段练习)为了评估某种药物的疗效,现有关部门对该药物在人体血管中的药物浓度进行测量.设该药物在人体血管中药物浓度与时间的关系为,甲、乙两人服用该药物后,血管中药物浓度随时间变化的关系如下图所示,则下列四个结论中正确的是( )
A.在时刻,甲、乙两人血管中的药物浓度的瞬时变化率相同.
B.在内,甲、乙两人血管中药物浓度的平均变化率不相同.
C.若,则在时刻,甲、乙两人血管中药物浓度的瞬时变化率一定不同
D.若,则在时刻,甲血管中药物浓度不高于乙血管中药物浓度
答案:D
【解析】对于A选项,在时刻,两曲线交于同一点,说明甲、乙两人血管中的药物浓度相同,瞬时变化率为切线的斜率,故不相同,故A错误;
对于B选项,在两个时刻,甲、乙两人血管中药物浓度相同,因此在这个时间段内,甲、乙两人血管中药物浓度的平均变化率相同,故B错误;
对于C选项, 这个时间段内,在时刻时,甲血管中药物浓度的瞬时变化率大于乙血管中药物浓度的瞬时变化率,在时刻时,甲血管中药物浓度的瞬时变化率小于乙血管中药物浓度的瞬时变化率,故存在使得甲、乙两人血管中药物浓度的瞬时变化率相同,故C错误;
对于D选项,在内,乙血管中药物浓度始终大于甲血管中药物浓度,在时刻,甲乙血管中药物浓度相同,故若,则在时刻,甲血管中药物浓度不高于乙血管中药物浓度,D正确.故选:D.
【一隅三反】
1.(2022·北京市育英学校高二期中)已知某物体运动的位移关于时间的函数为,则当时的瞬时速度是( )
A.5m/s B.4m/s C.3m/s D.2m/s
答案:A
【解析】因为,所以当时的瞬时速度是.故选:A
2.(2022·全国·高二课时练习)某物体的运动路程s(单位:m)与时间t(单位:s)的关系可用函数表示,则物体在t=0 s时的瞬时速度为______m/s;瞬时速度为9 m/s的时刻是在t=______s时.
答案: 1 4
【解析】,
即物体在t=0 s时的瞬时速度为1 m/s.设物体在时刻的瞬时速度为9 m/s,
又,
所以,物体在t=4 s时的瞬时速度为9 m/s.故答案为:1;4
3.(2022·北京通州·高二期中)假设某高山滑雪运动员在一次高山滑雪训练中滑行的路程l(单位:m)与时间t(单位:s)之间的函数关系为,则该运动员在这段时间的平均速度为______m/s;在时的瞬时速度为______m/s.
答案:
【解析】答题空1:该运动员在这段时间的平均速度为:
答题空2:由得,当时,.
故答案为:,
考点三 某处导数
【例3-1】(2022·广东·南海中学高二期中)设,则( )
A. B. C.4 D.8
答案:C
【解析】
故选:C
【例3-2】.(2022·山东·文登新一中高二期中)设存在导函数且满足,则曲线上的点处的切线的斜率为( )
A. B. C.1 D.2
答案:A
【解析】因为存在导函数且满足,
所以,即曲线上的点处的切线的斜率为,
故选:A.
【一隅三反】
1.(2022·全国·高三专题练习)若函数在处的导数为2,则 ( )
A.2 B.1 C. D.6
答案:B
【解析】由函数在处的导数为2,得,
所以,故选:B
2.(2022·天津市武清区杨村第一中学高二阶段练习)设函数,则( )
A.1 B.5 C. D.0
答案:B
【解析】由题意,所以,所以原式等于.
故选:B.
3.(2022·全国·高二课时练习)已知函数的导函数为,且,则实数的值为( )
A. B. C. D.
答案:D
【解析】,解得故选:D
考点四 导数的几何意义及应用
【例4-1】(2021·江苏·南京市中华中学高二期中)已如函数在处的切线斜率为2,则 等于( )
A.2 B.1 C.4 D.12
答案:C
【解析】函数在处的切线斜率为2,所以,
所以.故选:C
【例4-2】(2021·全国·高二课时练习)函数的图象在点处的切线的倾斜角的大小为______.
答案:135°
【解析】,即函数的图象在点处的切线的斜率为-1,所以切线的倾斜角.
故答案为:135°
【一隅三反】
1.(2021·全国·高二课前预习)抛物线y=x2+1在点(1,2)处的切线的斜率是________.
答案:2
【解析】k= = (2+Δx)=2.答案 2
2.(2022·全国高二课时练习)曲线y=x+上任意一点P处的切线斜率为k,则k的取值范围是
答案:(-∞,1)
【解析】上任意一点P(x0,y0)处的切线斜率为
== =<1,即k<1.
3.(2022广东)曲线y=x2-2在点x=1处的切线的倾斜角为( )
A.30° B.45° C.135° D.165°
答案:B
【解析】因为,故,故,
设曲线在处的切线的倾斜角为,则,而,故,故选:B.
4.(2022·全国·高二课时练习)(多选)若当,满足,则下列结论正确的是( )
A.
B.
C.曲线上点处的切线斜率为
D.曲线上点处的切线斜率为
答案:AD
【解析】由得:,即,
曲线上点处的切线斜率为,C错误;D正确;
,A正确;B错误.故选:AD.
