数学:第十五章一次函数章节测试题(一)(15.4~15.6)(北京课改版八年级下)
文档属性
| 名称 | 数学:第十五章一次函数章节测试题(一)(15.4~15.6)(北京课改版八年级下) | 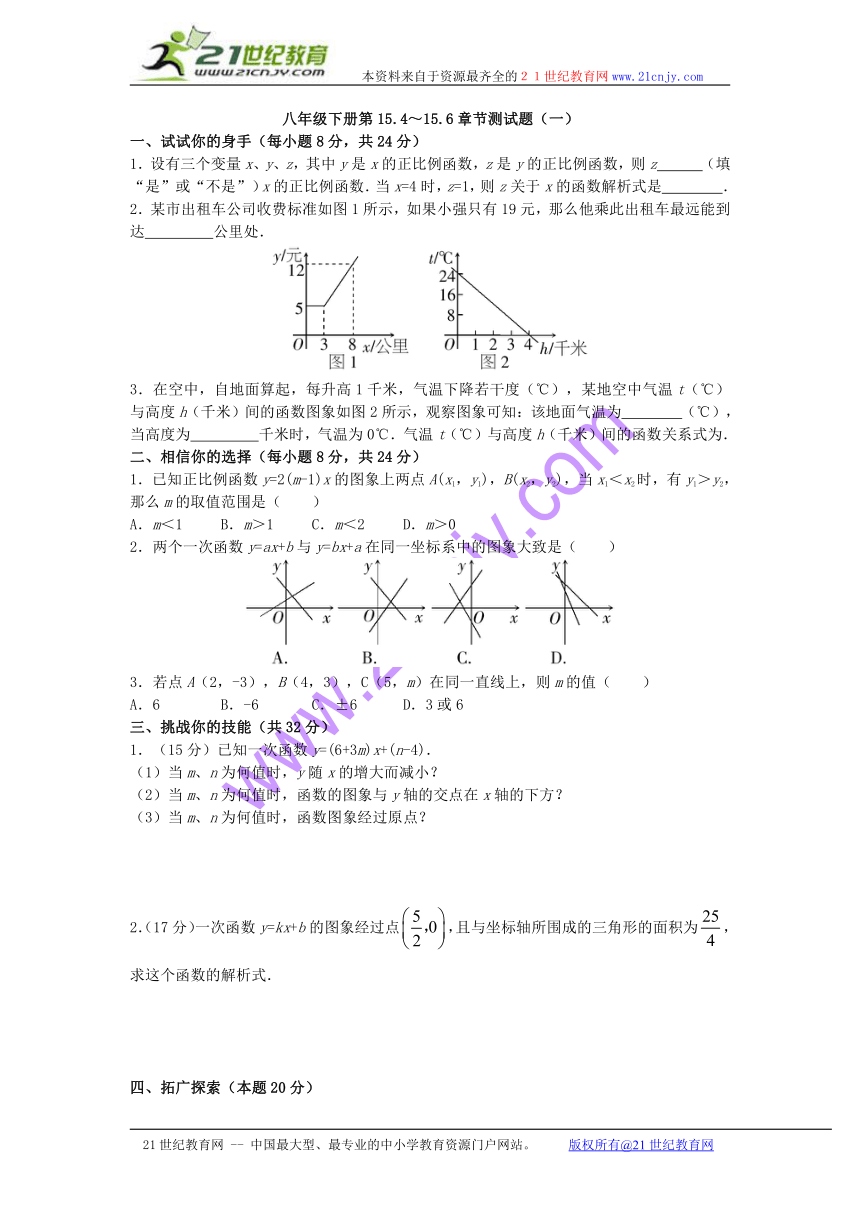 | |
| 格式 | rar | ||
| 文件大小 | 35.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 京教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-04-09 22:05:15 | ||
图片预览

文档简介
本资料来自于资源最齐全的21世纪教育网www.21cnjy.com
八年级下册第15.4~15.6章节测试题(一)
一、试试你的身手(每小题8分,共24分)
1.设有三个变量x、y、z,其中y是x的正比例函数,z是y的正比例函数,则z (填“是”或“不是”)x的正比例函数.当x=4时,z=1,则z关于x的函数解析式是 .
2.某市出租车公司收费标准如图1所示,如果小强只有19元,那么他乘此出租车最远能到达 公里处.
3.在空中,自地面算起,每升高1千米,气温下降若干度(℃),某地空中气温t(℃)与高度h(千米)间的函数图象如图2所示,观察图象可知:该地面气温为 (℃),当高度为 千米时,气温为0℃.气温t(℃)与高度h(千米)间的函数关系式为.
二、相信你的选择(每小题8分,共24分)
1.已知正比例函数y=2(m-1)x的图象上两点A(x1,y1),B(x2,y2),当x1<x2时,有y1>y2,那么m的取值范围是( )
A.m<1 B.m>1 C.m<2 D.m>0
2.两个一次函数y=ax+b与y=bx+a在同一坐标系中的图象大致是( )
3.若点A(2,-3),B(4,3),C(5,m)在同一直线上,则m的值( )
A.6 B.-6 C.±6 D.3或6
三、挑战你的技能(共32分)
1.(15分)已知一次函数y=(6+3m)x+(n-4).
(1)当m、n为何值时,y随x的增大而减小?
(2)当m、n为何值时,函数的图象与y轴的交点在x轴的下方?
(3)当m、n为何值时,函数图象经过原点?
2.(17分)一次函数y=kx+b的图象经过点,且与坐标轴所围成的三角形的面积为,求这个函数的解析式.
四、拓广探索(本题20分)
黄石市的A县和B县急需某种原料分别为90吨和60吨,该市的C县和D县分别储存这种原料100吨和50吨,全部调配给A县和B县.已知C、D两县运这种原料到A、B两县的运费(元/吨)如下表所示.
出发地运费目的地 C D
A 35 40
B 30 45
(1)设C县运到A县的原料有x吨,求总运费W(元)与x(吨)的函数解析式,并写出自变量的取值范围.
(2)求最低总运费,并说明总运费最低的运送方案.
参考答案:
一、1.是, 2.13 3.24,4,
二、1.A 2.B 3.A
三、1.(1),为任意实数时,随的增大而减小;
(2)时,函数图象与轴的交点在轴下方;
(3)当,时,函数图象经过原点
2.或
四、(1).
自变量取值范围为;
(2)运送方案为县运40吨到县,60吨到县,县运50吨到县
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
八年级下册第15.4~15.6章节测试题(一)
一、试试你的身手(每小题8分,共24分)
1.设有三个变量x、y、z,其中y是x的正比例函数,z是y的正比例函数,则z (填“是”或“不是”)x的正比例函数.当x=4时,z=1,则z关于x的函数解析式是 .
2.某市出租车公司收费标准如图1所示,如果小强只有19元,那么他乘此出租车最远能到达 公里处.
3.在空中,自地面算起,每升高1千米,气温下降若干度(℃),某地空中气温t(℃)与高度h(千米)间的函数图象如图2所示,观察图象可知:该地面气温为 (℃),当高度为 千米时,气温为0℃.气温t(℃)与高度h(千米)间的函数关系式为.
二、相信你的选择(每小题8分,共24分)
1.已知正比例函数y=2(m-1)x的图象上两点A(x1,y1),B(x2,y2),当x1<x2时,有y1>y2,那么m的取值范围是( )
A.m<1 B.m>1 C.m<2 D.m>0
2.两个一次函数y=ax+b与y=bx+a在同一坐标系中的图象大致是( )
3.若点A(2,-3),B(4,3),C(5,m)在同一直线上,则m的值( )
A.6 B.-6 C.±6 D.3或6
三、挑战你的技能(共32分)
1.(15分)已知一次函数y=(6+3m)x+(n-4).
(1)当m、n为何值时,y随x的增大而减小?
(2)当m、n为何值时,函数的图象与y轴的交点在x轴的下方?
(3)当m、n为何值时,函数图象经过原点?
2.(17分)一次函数y=kx+b的图象经过点,且与坐标轴所围成的三角形的面积为,求这个函数的解析式.
四、拓广探索(本题20分)
黄石市的A县和B县急需某种原料分别为90吨和60吨,该市的C县和D县分别储存这种原料100吨和50吨,全部调配给A县和B县.已知C、D两县运这种原料到A、B两县的运费(元/吨)如下表所示.
出发地运费目的地 C D
A 35 40
B 30 45
(1)设C县运到A县的原料有x吨,求总运费W(元)与x(吨)的函数解析式,并写出自变量的取值范围.
(2)求最低总运费,并说明总运费最低的运送方案.
参考答案:
一、1.是, 2.13 3.24,4,
二、1.A 2.B 3.A
三、1.(1),为任意实数时,随的增大而减小;
(2)时,函数图象与轴的交点在轴下方;
(3)当,时,函数图象经过原点
2.或
四、(1).
自变量取值范围为;
(2)运送方案为县运40吨到县,60吨到县,县运50吨到县
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
同课章节目录
