2023-2024学年人教版数学九年级下册 期末复习冲刺卷(含答案)
文档属性
| 名称 | 2023-2024学年人教版数学九年级下册 期末复习冲刺卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 642.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-28 08:32:33 | ||
图片预览

文档简介
2023-2024学年人教版数学九年级下册 期末复习冲刺卷
一、单选题
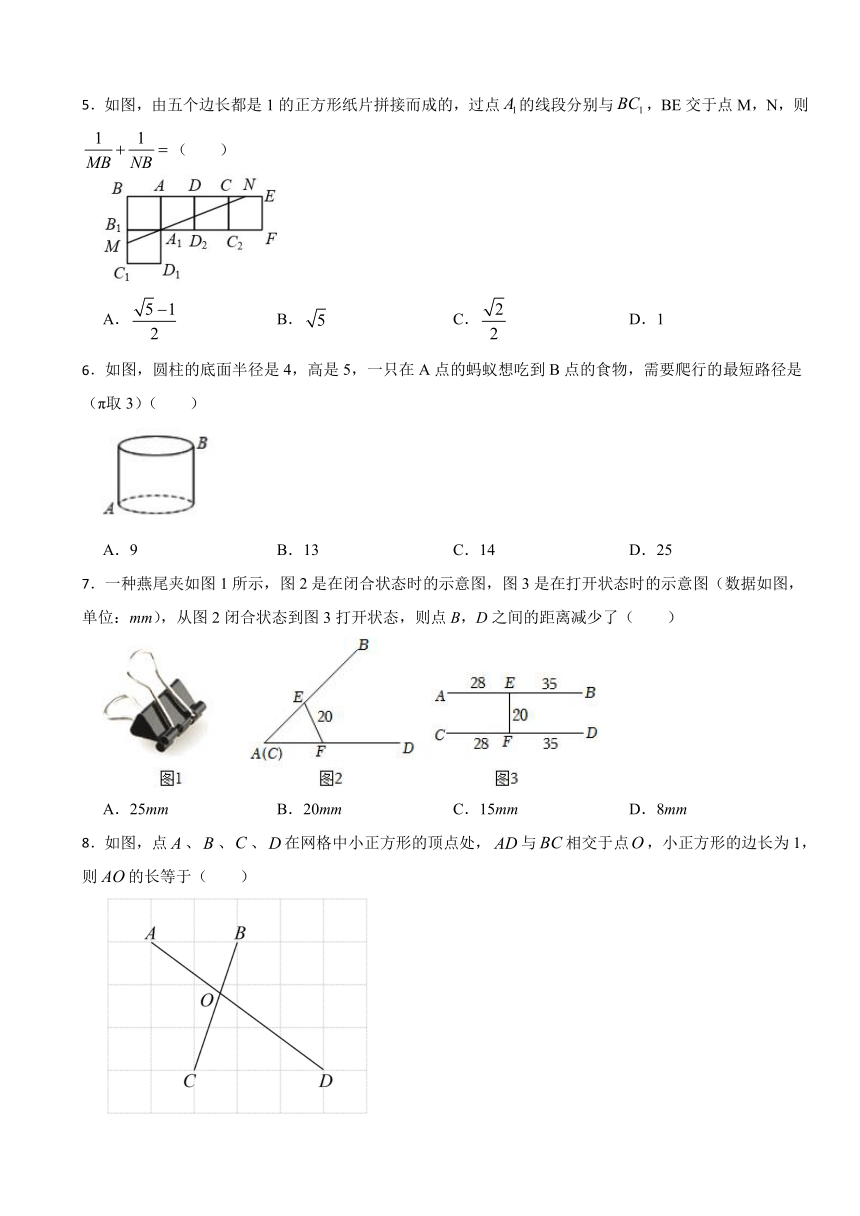
1.一个几何体的三视图如图所示,则这个几何体的表面积是( )
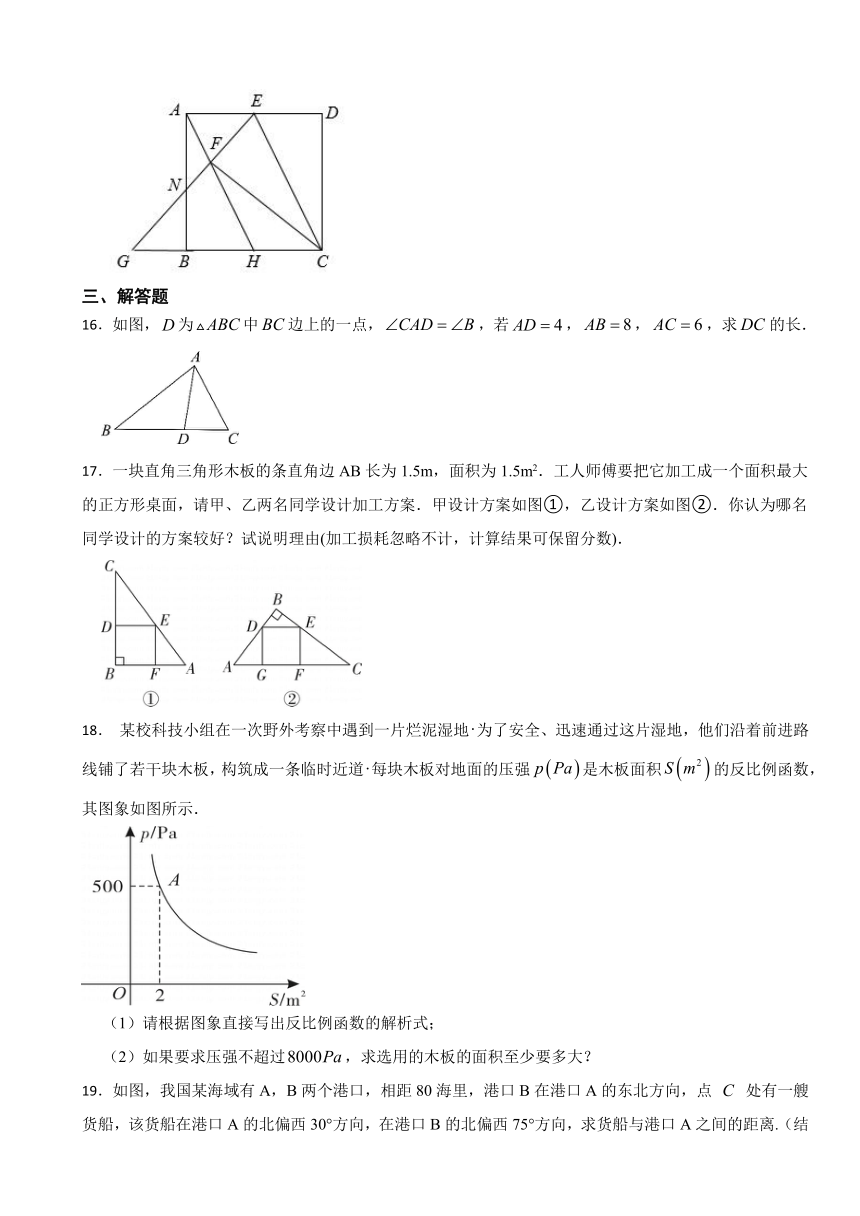
A. B. C. D.
2.已知如图,一次函数y=ax+b和反比例函数y= 的图象相交于A、B两点,不等式ax+b> 的解集为( )
A.x< 3 B. 31
C.x< 3或x>1 D. 33. 点,,都在反比例函数的图象上,则,,的大小关系是( )
A. B. C. D.
4.按照如图的平面展开图折叠成正方体后,相对面上的两个数都互为相反数,那么(a+c)b的值等于( )
A.1 B. C.3 D.
5.如图,由五个边长都是1的正方形纸片拼接而成的,过点的线段分别与,BE交于点M,N,则( )
A. B. C. D.1
6.如图,圆柱的底面半径是4,高是5,一只在A点的蚂蚁想吃到B点的食物,需要爬行的最短路径是(π取3)( )
A.9 B.13 C.14 D.25
7.一种燕尾夹如图1所示,图2是在闭合状态时的示意图,图3是在打开状态时的示意图(数据如图,单位:mm),从图2闭合状态到图3打开状态,则点B,D之间的距离减少了( )
A.25mm B.20mm C.15mm D.8mm
8.如图,点、、、在网格中小正方形的顶点处,与相交于点,小正方形的边长为1,则的长等于( )
A.2 B. C. D.
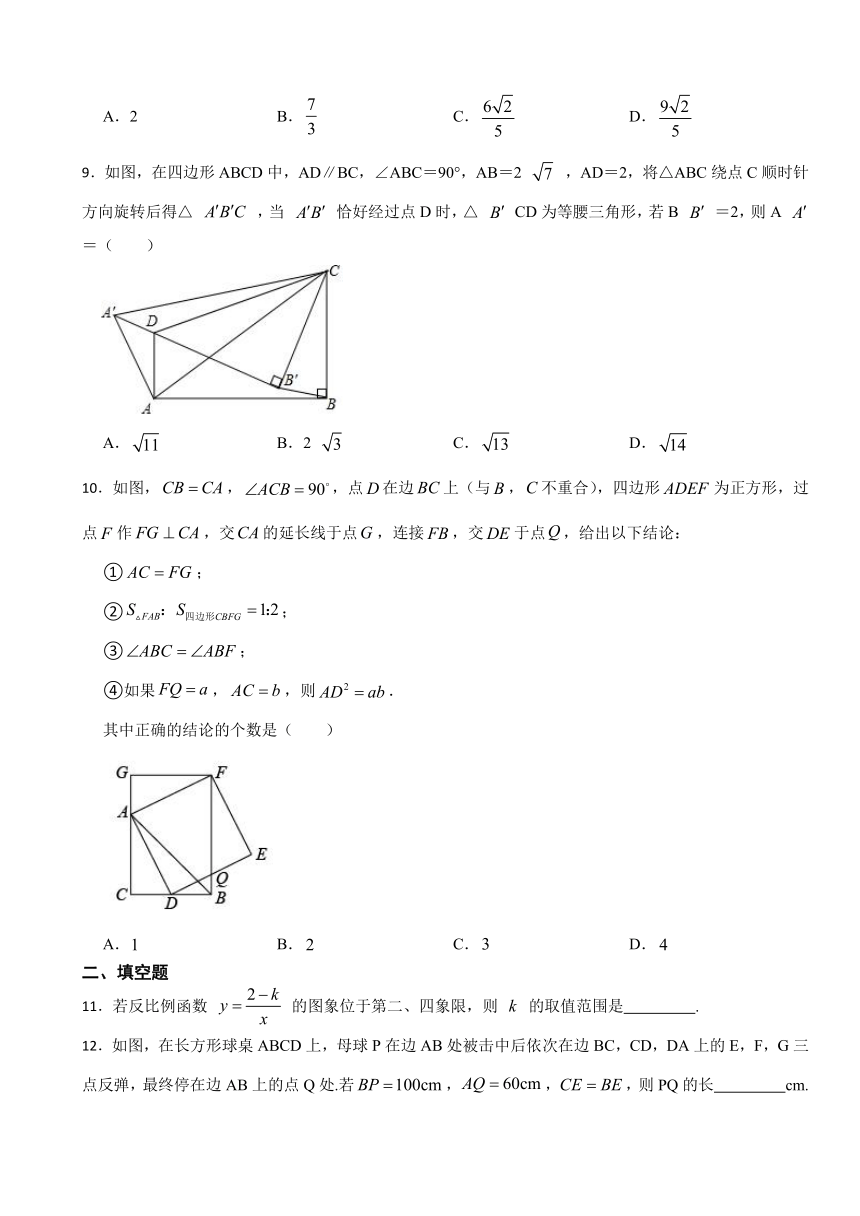
9.如图,在四边形ABCD中,AD∥BC,∠ABC=90°,AB=2 ,AD=2,将△ABC绕点C顺时针方向旋转后得△ ,当 恰好经过点D时,△ CD为等腰三角形,若B =2,则A =( )
A. B.2 C. D.
10.如图,,,点在边上(与,不重合),四边形为正方形,过点作,交的延长线于点,连接,交于点,给出以下结论:
①;
②;
③;
④如果,,则.
其中正确的结论的个数是( )
A. B. C. D.
二、填空题
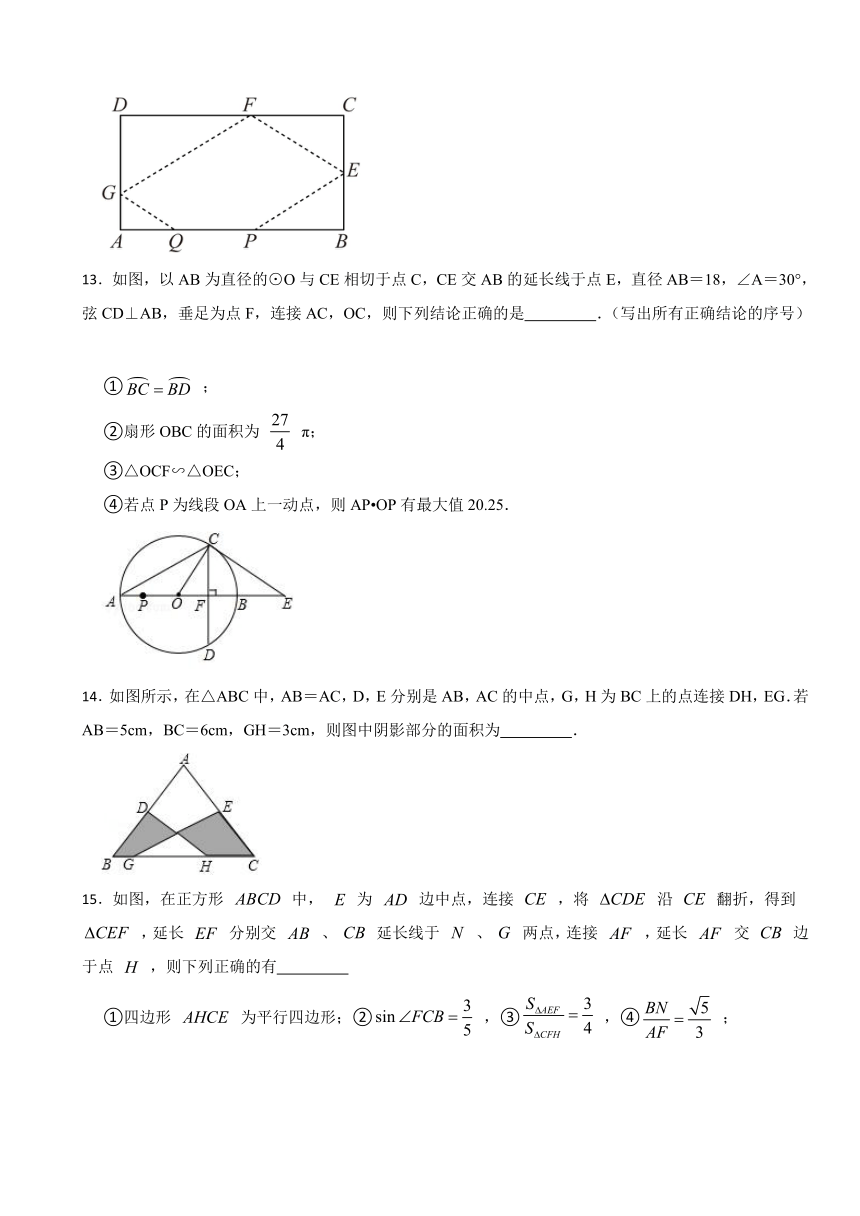
11.若反比例函数 的图象位于第二、四象限,则 的取值范围是 .
12.如图,在长方形球桌ABCD上,母球P在边AB处被击中后依次在边BC,CD,DA上的E,F,G三点反弹,最终停在边AB上的点Q处.若,,,则PQ的长 cm.
13.如图,以AB为直径的⊙O与CE相切于点C,CE交AB的延长线于点E,直径AB=18,∠A=30°,弦CD⊥AB,垂足为点F,连接AC,OC,则下列结论正确的是 .(写出所有正确结论的序号)
① ;
②扇形OBC的面积为 π;
③△OCF∽△OEC;
④若点P为线段OA上一动点,则AP OP有最大值20.25.
14.如图所示,在△ABC中,AB=AC,D,E分别是AB,AC的中点,G,H为BC上的点连接DH,EG.若AB=5cm,BC=6cm,GH=3cm,则图中阴影部分的面积为 .
15.如图,在正方形 中, 为 边中点,连接 ,将 沿 翻折,得到 ,延长 分别交 、 延长线于 、 两点,连接 ,延长 交 边于点 ,则下列正确的有
①四边形 为平行四边形;② ,③ ,④ ;
三、解答题
16.如图,为中边上的一点,,若,,,求的长.
17.一块直角三角形木板的条直角边AB长为1.5m,面积为1.5m2.工人师傅要把它加工成一个面积最大的正方形桌面,请甲、乙两名同学设计加工方案.甲设计方案如图①,乙设计方案如图②.你认为哪名同学设计的方案较好?试说明理由(加工损耗忽略不计,计算结果可保留分数).
18. 某校科技小组在一次野外考察中遇到一片烂泥湿地为了安全、迅速通过这片湿地,他们沿着前进路线铺了若干块木板,构筑成一条临时近道每块木板对地面的压强是木板面积的反比例函数,其图象如图所示.
(1)请根据图象直接写出反比例函数的解析式;
(2)如果要求压强不超过,求选用的木板的面积至少要多大?
19.如图,我国某海域有A,B两个港口,相距80海里,港口B在港口A的东北方向,点 处有一艘货船,该货船在港口A的北偏西30°方向,在港口B的北偏西75°方向,求货船与港口A之间的距离.(结果保留根号)
20.若 ,且x+2y+z=36,分别求x、y、z的值.
21.“今有邑,东西七里,南北九里,各开中门,出东门一十五里有木,问:出南门几何步而见木?”这段话摘自《九章算术》,意思是说:如图,矩形城池ABCD,东边城墙AB长9里,南边城墙AD长7里,东门点E,南门点F分别是AB、AD的中点,EG⊥AB,FH⊥AD,EG=15里,HG经过点A,问FH多少里?
22.若a、b、c是非零实数,且满足 ,直线y=kx+b经过点(4,0),求直线y=kx+b与两坐标轴所围成的三角形的面积.
23. 如图,在平行四边形中,对角线与相交于点O,.
(1)过点B作交于点E(如图1).
①求证:;
②若,,求的长;
(2)如图(2),若,点E,H分别在边,上,与相交于点G,交于点F,且,求证:
答案部分
1.【答案】D
2.【答案】B
3.【答案】A
4.【答案】B
5.【答案】D
6.【答案】B
7.【答案】A
8.【答案】A
9.【答案】A
10.【答案】D
11.【答案】k>2
12.【答案】80
13.【答案】①③④
14.【答案】6cm2
15.【答案】①②④
16.【答案】解:在和中,,
,
,
,,,
,
解得,
故的长为3.
17.【答案】由AB=1.5m,S△ABC=1.5m2 ,可得BC=2m.
由图①,设甲设计的正方形桌面边长为x(m),由DE∥AB,得Rt△CDE∽Rt△CBA,
∴,即5=,解得x=
由图②,过点B作Rt△ABC斜边AC上的高线BH,交DE于点P ,交AC于点H.
由AB=1。5m,BC=2m,得AC==2.5(m).
由AC·BH=AB·BC,得BH==1.2(m).设乙设计的桌面的边长为y(m),
∵ DE∥AC,∴Rt△BDE∽Rt△BAC,∴,即,解得y=
∵>.∴甲同学设计的方案较好.
18.【答案】(1)解:由图象得:双曲线过点,在第一象限,
,
反比例函数表达式为:;
(2)解:当时:,即:;
由图象可知,随着的增大而减小,
当时,,
选用的木板的面积至少要.
19.【答案】解:过点A作 于点D
根据题意,得
∵
∴
∴
在 中
∵ ,
∴
∵
∴
在 中
∵ ,
∴
答:货船与港口A之间的距离是 海里.
20.【答案】解:设 =k,
∴x=2k,y=3k,z=4k,
代入x+2y+z=36得:2k+6k+4k=36,
解得:k=3,
所以x=6,y=9,z=12.
21.【答案】解:∵EG⊥AB,FH⊥AD,HG经过点A,
∴FA∥EG,EA∥FH,
∴∠AEG=∠HFA=90°,∠EAG=∠FHA,
∴△GEA∽△AFH,
∴ .
∵AB=9里,AD=7里,EG=15里,
∴AF=3.5里,AE=4.5里,
∴ ,
∴FH=1.05里.
22.【答案】解:∵∴a=(b+c)k,b=(a+c)k,c=(a+b)k,∴a+b+c=2(a+b+c)k,∴①当a+b+c≠0时,k= ,∴y=kx+b变为:y= x+b,∵经过点(4,0),∴ ×4+b=0,b=-2,∴y= x-2,图象如图:S△ABO= ×AO×BO= ×2×4=4.②当a+b+c=0时,a=-(b+c),k= =-1同法可请求:y=-x+4,S△ADO=8,即直线y=kx+b与两坐标轴所围成的三角形的面积是4或8
23.【答案】(1)解:①证明:∵,∴,
∵四边形是平行四边形,∴四边形是菱形,
∴
②解:∵四边形是平行四边形,
∴,
∵,,
∴,
∴,
∵,,
∴,
∴,
∴,∴,解得:.
(2)解:∵,,,
∴,
∴
∴,
∴,
∴,∴,
∴,∵
∴
一、单选题
1.一个几何体的三视图如图所示,则这个几何体的表面积是( )
A. B. C. D.
2.已知如图,一次函数y=ax+b和反比例函数y= 的图象相交于A、B两点,不等式ax+b> 的解集为( )
A.x< 3 B. 3
C.x< 3或x>1 D. 3
A. B. C. D.
4.按照如图的平面展开图折叠成正方体后,相对面上的两个数都互为相反数,那么(a+c)b的值等于( )
A.1 B. C.3 D.
5.如图,由五个边长都是1的正方形纸片拼接而成的,过点的线段分别与,BE交于点M,N,则( )
A. B. C. D.1
6.如图,圆柱的底面半径是4,高是5,一只在A点的蚂蚁想吃到B点的食物,需要爬行的最短路径是(π取3)( )
A.9 B.13 C.14 D.25
7.一种燕尾夹如图1所示,图2是在闭合状态时的示意图,图3是在打开状态时的示意图(数据如图,单位:mm),从图2闭合状态到图3打开状态,则点B,D之间的距离减少了( )
A.25mm B.20mm C.15mm D.8mm
8.如图,点、、、在网格中小正方形的顶点处,与相交于点,小正方形的边长为1,则的长等于( )
A.2 B. C. D.
9.如图,在四边形ABCD中,AD∥BC,∠ABC=90°,AB=2 ,AD=2,将△ABC绕点C顺时针方向旋转后得△ ,当 恰好经过点D时,△ CD为等腰三角形,若B =2,则A =( )
A. B.2 C. D.
10.如图,,,点在边上(与,不重合),四边形为正方形,过点作,交的延长线于点,连接,交于点,给出以下结论:
①;
②;
③;
④如果,,则.
其中正确的结论的个数是( )
A. B. C. D.
二、填空题
11.若反比例函数 的图象位于第二、四象限,则 的取值范围是 .
12.如图,在长方形球桌ABCD上,母球P在边AB处被击中后依次在边BC,CD,DA上的E,F,G三点反弹,最终停在边AB上的点Q处.若,,,则PQ的长 cm.
13.如图,以AB为直径的⊙O与CE相切于点C,CE交AB的延长线于点E,直径AB=18,∠A=30°,弦CD⊥AB,垂足为点F,连接AC,OC,则下列结论正确的是 .(写出所有正确结论的序号)
① ;
②扇形OBC的面积为 π;
③△OCF∽△OEC;
④若点P为线段OA上一动点,则AP OP有最大值20.25.
14.如图所示,在△ABC中,AB=AC,D,E分别是AB,AC的中点,G,H为BC上的点连接DH,EG.若AB=5cm,BC=6cm,GH=3cm,则图中阴影部分的面积为 .
15.如图,在正方形 中, 为 边中点,连接 ,将 沿 翻折,得到 ,延长 分别交 、 延长线于 、 两点,连接 ,延长 交 边于点 ,则下列正确的有
①四边形 为平行四边形;② ,③ ,④ ;
三、解答题
16.如图,为中边上的一点,,若,,,求的长.
17.一块直角三角形木板的条直角边AB长为1.5m,面积为1.5m2.工人师傅要把它加工成一个面积最大的正方形桌面,请甲、乙两名同学设计加工方案.甲设计方案如图①,乙设计方案如图②.你认为哪名同学设计的方案较好?试说明理由(加工损耗忽略不计,计算结果可保留分数).
18. 某校科技小组在一次野外考察中遇到一片烂泥湿地为了安全、迅速通过这片湿地,他们沿着前进路线铺了若干块木板,构筑成一条临时近道每块木板对地面的压强是木板面积的反比例函数,其图象如图所示.
(1)请根据图象直接写出反比例函数的解析式;
(2)如果要求压强不超过,求选用的木板的面积至少要多大?
19.如图,我国某海域有A,B两个港口,相距80海里,港口B在港口A的东北方向,点 处有一艘货船,该货船在港口A的北偏西30°方向,在港口B的北偏西75°方向,求货船与港口A之间的距离.(结果保留根号)
20.若 ,且x+2y+z=36,分别求x、y、z的值.
21.“今有邑,东西七里,南北九里,各开中门,出东门一十五里有木,问:出南门几何步而见木?”这段话摘自《九章算术》,意思是说:如图,矩形城池ABCD,东边城墙AB长9里,南边城墙AD长7里,东门点E,南门点F分别是AB、AD的中点,EG⊥AB,FH⊥AD,EG=15里,HG经过点A,问FH多少里?
22.若a、b、c是非零实数,且满足 ,直线y=kx+b经过点(4,0),求直线y=kx+b与两坐标轴所围成的三角形的面积.
23. 如图,在平行四边形中,对角线与相交于点O,.
(1)过点B作交于点E(如图1).
①求证:;
②若,,求的长;
(2)如图(2),若,点E,H分别在边,上,与相交于点G,交于点F,且,求证:
答案部分
1.【答案】D
2.【答案】B
3.【答案】A
4.【答案】B
5.【答案】D
6.【答案】B
7.【答案】A
8.【答案】A
9.【答案】A
10.【答案】D
11.【答案】k>2
12.【答案】80
13.【答案】①③④
14.【答案】6cm2
15.【答案】①②④
16.【答案】解:在和中,,
,
,
,,,
,
解得,
故的长为3.
17.【答案】由AB=1.5m,S△ABC=1.5m2 ,可得BC=2m.
由图①,设甲设计的正方形桌面边长为x(m),由DE∥AB,得Rt△CDE∽Rt△CBA,
∴,即5=,解得x=
由图②,过点B作Rt△ABC斜边AC上的高线BH,交DE于点P ,交AC于点H.
由AB=1。5m,BC=2m,得AC==2.5(m).
由AC·BH=AB·BC,得BH==1.2(m).设乙设计的桌面的边长为y(m),
∵ DE∥AC,∴Rt△BDE∽Rt△BAC,∴,即,解得y=
∵>.∴甲同学设计的方案较好.
18.【答案】(1)解:由图象得:双曲线过点,在第一象限,
,
反比例函数表达式为:;
(2)解:当时:,即:;
由图象可知,随着的增大而减小,
当时,,
选用的木板的面积至少要.
19.【答案】解:过点A作 于点D
根据题意,得
∵
∴
∴
在 中
∵ ,
∴
∵
∴
在 中
∵ ,
∴
答:货船与港口A之间的距离是 海里.
20.【答案】解:设 =k,
∴x=2k,y=3k,z=4k,
代入x+2y+z=36得:2k+6k+4k=36,
解得:k=3,
所以x=6,y=9,z=12.
21.【答案】解:∵EG⊥AB,FH⊥AD,HG经过点A,
∴FA∥EG,EA∥FH,
∴∠AEG=∠HFA=90°,∠EAG=∠FHA,
∴△GEA∽△AFH,
∴ .
∵AB=9里,AD=7里,EG=15里,
∴AF=3.5里,AE=4.5里,
∴ ,
∴FH=1.05里.
22.【答案】解:∵∴a=(b+c)k,b=(a+c)k,c=(a+b)k,∴a+b+c=2(a+b+c)k,∴①当a+b+c≠0时,k= ,∴y=kx+b变为:y= x+b,∵经过点(4,0),∴ ×4+b=0,b=-2,∴y= x-2,图象如图:S△ABO= ×AO×BO= ×2×4=4.②当a+b+c=0时,a=-(b+c),k= =-1同法可请求:y=-x+4,S△ADO=8,即直线y=kx+b与两坐标轴所围成的三角形的面积是4或8
23.【答案】(1)解:①证明:∵,∴,
∵四边形是平行四边形,∴四边形是菱形,
∴
②解:∵四边形是平行四边形,
∴,
∵,,
∴,
∴,
∵,,
∴,
∴,
∴,∴,解得:.
(2)解:∵,,,
∴,
∴
∴,
∴,
∴,∴,
∴,∵
∴
同课章节目录
