(人教A版2019选择性必修第二册)高二数学拓展1利用递推公式求通项公式常用的方法(精讲)(含解析)
文档属性
| 名称 | (人教A版2019选择性必修第二册)高二数学拓展1利用递推公式求通项公式常用的方法(精讲)(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-28 00:00:00 | ||
图片预览

文档简介
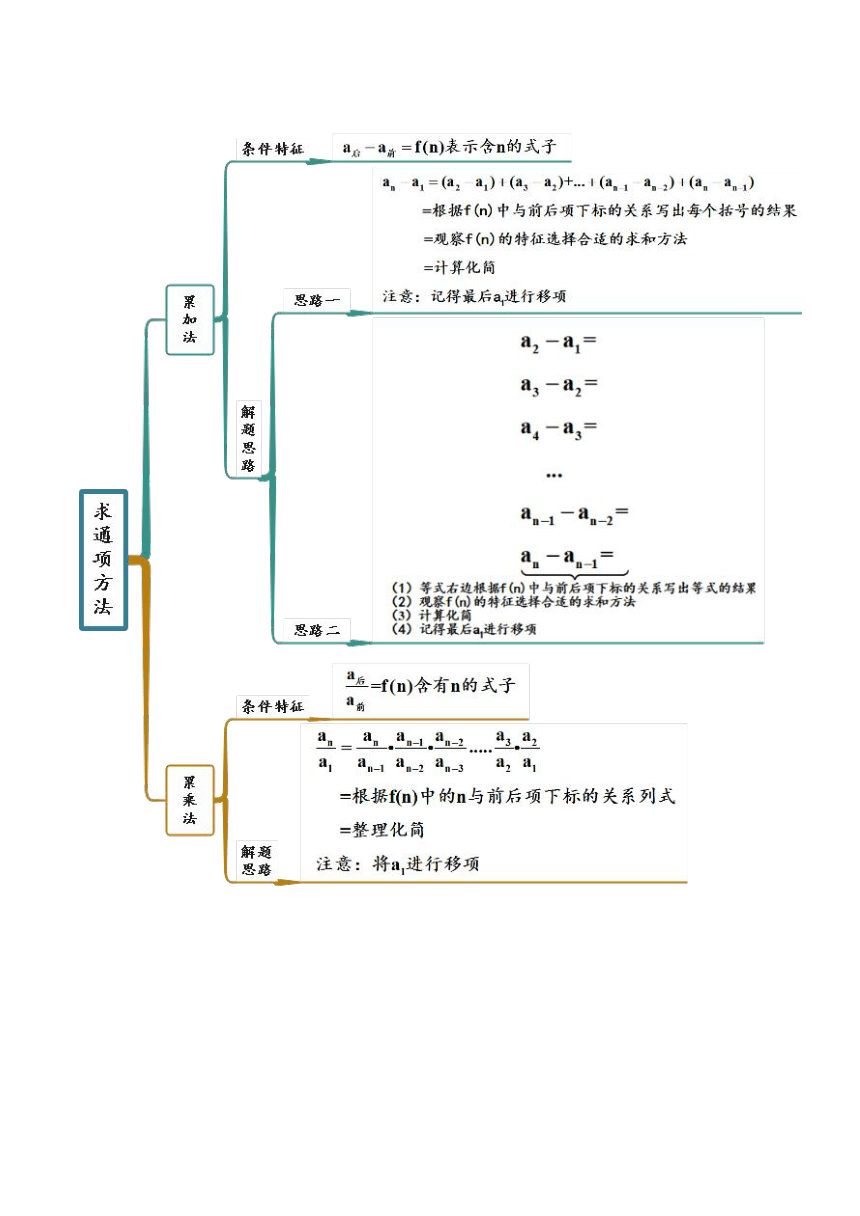
拓展1 利用递推公式求通项公式常用的方法(精讲)
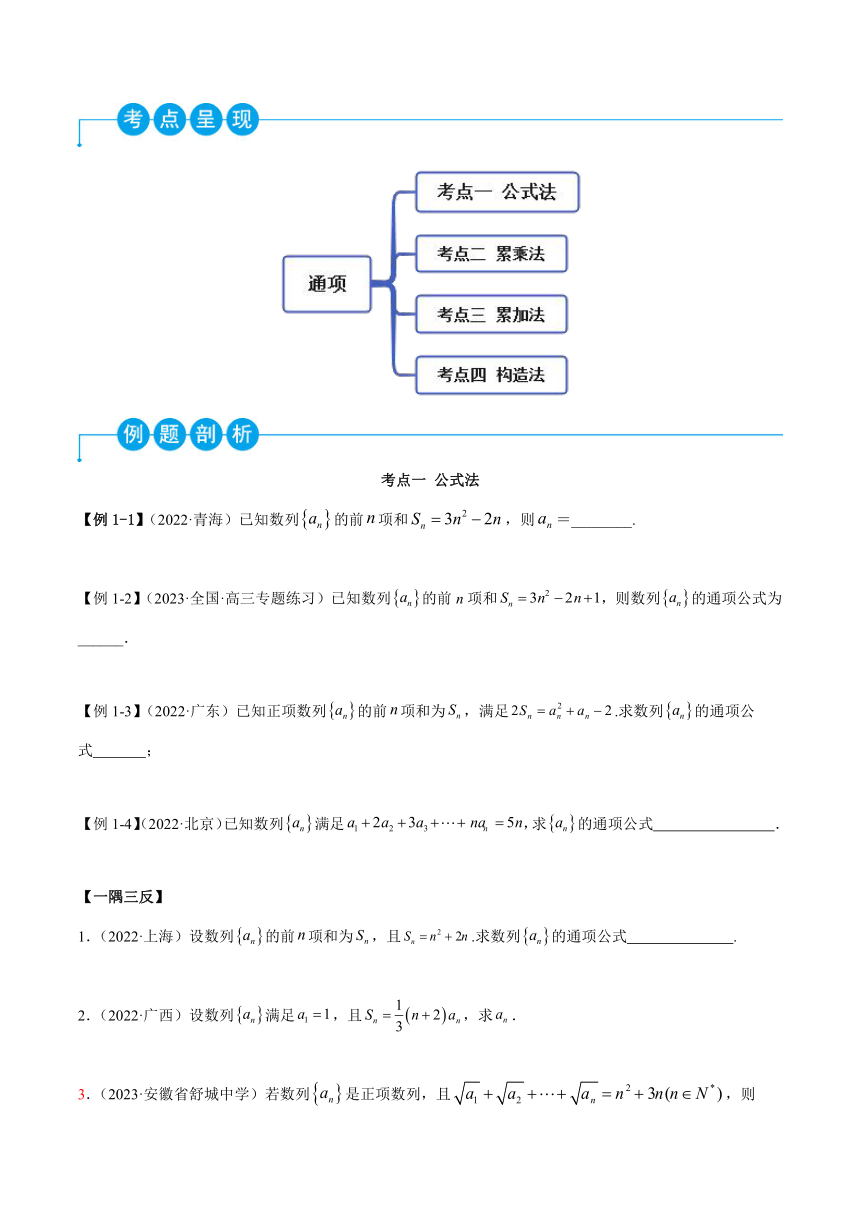
考点一 公式法
【例1-1】(2022·青海)已知数列的前项和,则=________.
【例1-2】(2023·全国·高三专题练习)已知数列的前n项和,则数列的通项公式为______.
【例1-3】(2022·广东)已知正项数列的前项和为,满足.求数列的通项公式 ;
【例1-4】(2022·北京)已知数列满足,求的通项公式 .
【一隅三反】
1.(2022·上海)设数列的前项和为,且.求数列的通项公式 .
2.(2022·广西)设数列满足,且,求.
3.(2023·安徽省舒城中学)若数列是正项数列,且,则_______.
4.(2022·福建 )已知数列的前n项和为,且满足,则数列的通项公式为______.
考点二 累乘法
【例2-1】(2022·江苏)已知数列满足,,则数列的通项公式是
【例2-2](2022·湖南)已知,,则数列的通项公式是
【一隅三反】
1.(2022·全国·高三专题练习)已知数列满足,且,则( )
A. B. C. D.
2.(2022·全国·高二)已知数列满足, ,则数列的通项公式为( )
A. B. C. D.
3.(2022河北)已知数列的前n项和为,且满足,则数列的通项公式等于___________
考点三 累加法
【例3-1】(2022·黑龙江)已知数列满足,.
(1)求,;
(2)求数列的通项公式.
【例3-2】(2022·哈尔滨)在数列中,,,则等于( )
A. B.
C. D.
【一隅三反】
1.(2022山东)已知在数列的前项之和为,若,则_______.
2.(2022·云南)已知数列满足,,,求通项公式.
3.(2021·全国·高二课时练习)设{an}是首项为1的正项数列且-(n+1)-anan+1=0(n∈N*),求an.
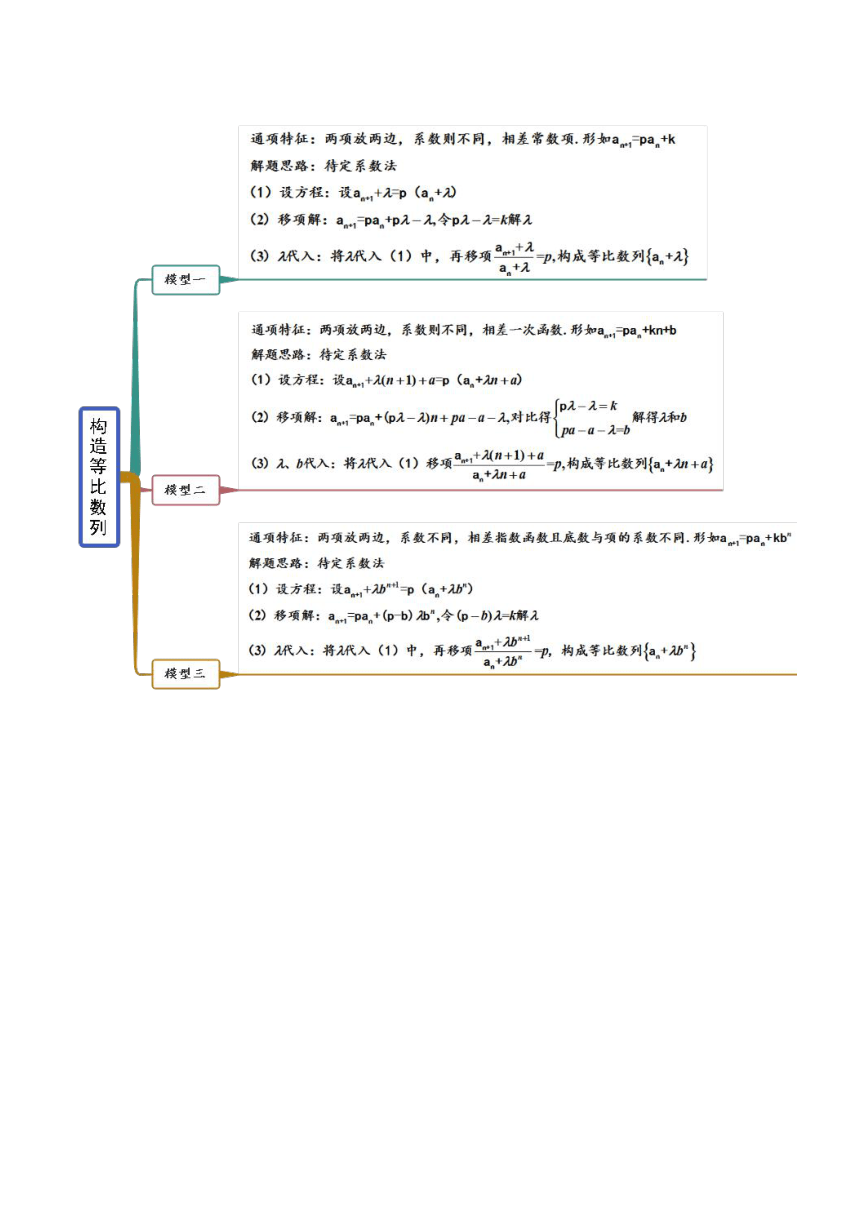
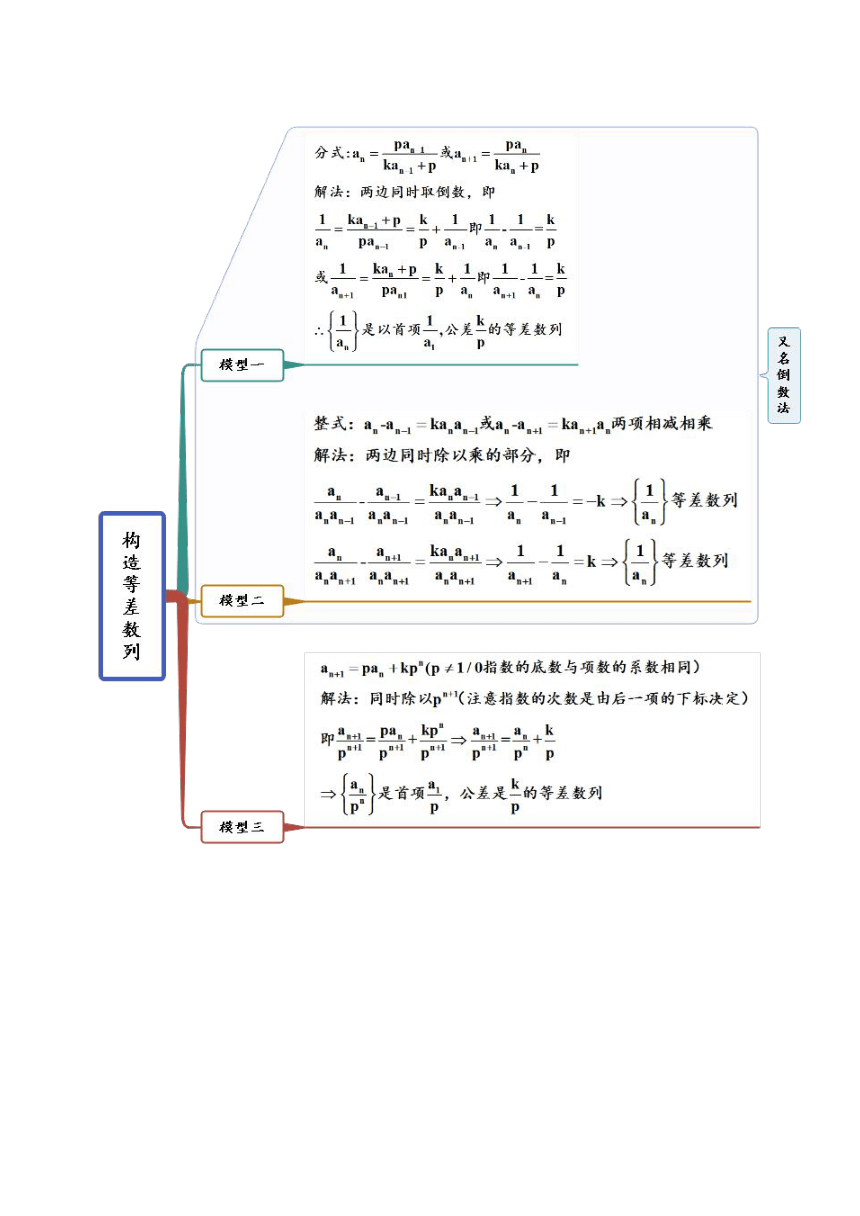
考点四 构造法
【例4-1】(2022·宁夏)已知数列中,,则等于
【例4-2】(2022·上海)已知数列满足,且,则数列的通项公式为______.
【例4-3】(2022·湖北)已知在数列中,,,则______.
【例4-4】(2022·江西)数列{an}满足,,则数列{an}的通项公式为___________.
【一隅三反】
1.(2022·青海)在数列中,,,则通项公式______.
2.(2022·山西)在数列中,若,则________.
3.(2022湖南)若数列满足,,则数列的通项公式________.
拓展1 利用递推公式求通项公式常用的方法(精讲)
考点一 公式法
【例1-1】(2022·青海)已知数列的前项和,则=________.
答案:
【解析】由于数列的前项和.
当时,;
当时,.
满足.因此,对任意的,.故答案为:.
【例1-2】(2023·全国·高三专题练习)已知数列的前n项和,则数列的通项公式为______.
答案:
【解析】因为,
当时,,
当时,,
所以.故答案为:.
【例1-3】(2022·广东)已知正项数列的前项和为,满足.求数列的通项公式 ;
答案:
【解析】①;
当时,代入①得.
当时,②;
①-②得,
整理得,
因为,所以,
所以数列为等差数列,公差为1,
所以.
【例1-4】(2022·北京)已知数列满足,求的通项公式 .
答案:.
【解析】对任意的,,
当时,则,
当时,由,可得,
上述两个等式作差可得,
,
满足,
因此,对任意的,.
【一隅三反】
1.(2022·上海)设数列的前项和为,且.求数列的通项公式 .
答案:
【解析】当时,;
当时,,
;
经检验:满足;
综上所述:.
2.(2022·广西)设数列满足,且,求.
答案:
【解析】当时,,
即,
两边同时除以,
得,
所以数列是常数数列,
所以,
所以.
3.(2023·安徽省舒城中学)若数列是正项数列,且,则_______.
答案:
【解析】数列是正项数列,且所以,即
时
两式相减得,
所以( )当时,适合上式,所以
4.(2022·福建 )已知数列的前n项和为,且满足,则数列的通项公式为______.
答案:
【解析】因为,所以,即.
当时,,
当时,,
显然不满足上式.
所以.
故答案为:.
考点二 累乘法
【例2-1】(2022·江苏)已知数列满足,,则数列的通项公式是
答案:
【解析】因为,
所以,,,,,,
所以,
即,又,所以;
故选:A
【】例2-2(2022·湖南)已知,,则数列的通项公式是
答案:n
【解析】由,得,
即,
则,,,…,,
由累乘法可得,所以,
又,符合上式,所以.
故选:D.
【一隅三反】
1.(2022·全国·高三专题练习)已知数列满足,且,则( )
A. B. C. D.
答案:D
【解析】数列满足,且,
∴,,
∴,,,,
累乘可得:,
可得:.
故选:D﹒
2.(2022·全国·高二)已知数列满足, ,则数列的通项公式为( )
A. B. C. D.
答案:A
【解析】由,得,
即,则,,,…,,
由累乘法可得,所以,
又,符合上式,所以.
故选:A.
3.(2022河北)已知数列的前n项和为,且满足,则数列的通项公式等于___________
答案:
【解析】由得:,当时,,
两式相减得:,化简整理得:,
当时,,即有,解得,因此,,,,
,
而满足上式,所以.故答案为:
考点三 累加法
【例3-1】(2022·黑龙江)已知数列满足,.
(1)求,;
(2)求数列的通项公式.
答案:(1),(2)
【解析】(1),,,.
(2)由得:,
,
又满足,.
【例3-2】(2022·哈尔滨)在数列中,,,则等于( )
A. B.
C. D.
答案:C
【解析】因,则有,
于是得,当时,
,
因此,,显然,满足上式,
所以.
故选:C
【一隅三反】
1.(2022山东)已知在数列的前项之和为,若,则_______.
答案:
【解析】 .
.
2.(2022·云南)已知数列满足,,,求通项公式.
答案:.
【解析】因为,
所以,
所以,
,
,
……,
,
所以,
因为,
所以,
所以,
因为满足上式,
所以.
3.(2021·全国·高二课时练习)设{an}是首项为1的正项数列且-(n+1)-anan+1=0(n∈N*),求an.
答案:an=n(n∈N*)
【解析】-(n+1)-anan+1=0(n∈N*),可得(an+1+an)[nan+1-(n+1)an]=0.
因为{an}是首项为1的正项数列,故an+1+an为正数,
故nan+1-(n+1)an=0,即=,
所以an=a1·=1.
且当时,符合an=n,所以an=n(n∈N*).
综上可知, an=n(n∈N*).
考点四 构造法
【例4-1】(2022·宁夏)已知数列中,,则等于
答案:
【解析】
所以所以数列是一个以2为首项,以4为公比的等比数列,
所以.故选:C
【例4-2】(2022·上海)已知数列满足,且,则数列的通项公式为______.
答案:
【解析】由两边取倒数可得,即.
所以数列是首项为2,公差为3等差数列.
所以,所以.
故答案为:.
【例4-3】(2022·湖北)已知在数列中,,,则______.
答案:
【解析】因为,,所以,
整理得,所以数列是以为首项,
为公比的等比数列,所以,解得.
故答案为:.
【例4-4】(2022·江西)数列{an}满足,,则数列{an}的通项公式为___________.
答案:.
【解析】∵,所以,即,
∴是等差数列,而,
所以,
所以.故答案为:.
【一隅三反】
1.(2022·青海)在数列中,,,则通项公式______.
答案:
【解析】由得:,又,
数列是以为首项,为公比的等比数列,
,则.
故答案为:.
2.(2022·山西)在数列中,若,则________.
答案:
【解析】取倒数得:,
所以数列是首项为1,公差为2的等差数列,
所以,所以.
故答案为:
3.(2022湖南)若数列满足,,则数列的通项公式________.
答案:
【解析】由,可得,设
则,则
所以是以1为首项,3为公比的等比数列.
则,则,所以
故答案为:
考点一 公式法
【例1-1】(2022·青海)已知数列的前项和,则=________.
【例1-2】(2023·全国·高三专题练习)已知数列的前n项和,则数列的通项公式为______.
【例1-3】(2022·广东)已知正项数列的前项和为,满足.求数列的通项公式 ;
【例1-4】(2022·北京)已知数列满足,求的通项公式 .
【一隅三反】
1.(2022·上海)设数列的前项和为,且.求数列的通项公式 .
2.(2022·广西)设数列满足,且,求.
3.(2023·安徽省舒城中学)若数列是正项数列,且,则_______.
4.(2022·福建 )已知数列的前n项和为,且满足,则数列的通项公式为______.
考点二 累乘法
【例2-1】(2022·江苏)已知数列满足,,则数列的通项公式是
【例2-2](2022·湖南)已知,,则数列的通项公式是
【一隅三反】
1.(2022·全国·高三专题练习)已知数列满足,且,则( )
A. B. C. D.
2.(2022·全国·高二)已知数列满足, ,则数列的通项公式为( )
A. B. C. D.
3.(2022河北)已知数列的前n项和为,且满足,则数列的通项公式等于___________
考点三 累加法
【例3-1】(2022·黑龙江)已知数列满足,.
(1)求,;
(2)求数列的通项公式.
【例3-2】(2022·哈尔滨)在数列中,,,则等于( )
A. B.
C. D.
【一隅三反】
1.(2022山东)已知在数列的前项之和为,若,则_______.
2.(2022·云南)已知数列满足,,,求通项公式.
3.(2021·全国·高二课时练习)设{an}是首项为1的正项数列且-(n+1)-anan+1=0(n∈N*),求an.
考点四 构造法
【例4-1】(2022·宁夏)已知数列中,,则等于
【例4-2】(2022·上海)已知数列满足,且,则数列的通项公式为______.
【例4-3】(2022·湖北)已知在数列中,,,则______.
【例4-4】(2022·江西)数列{an}满足,,则数列{an}的通项公式为___________.
【一隅三反】
1.(2022·青海)在数列中,,,则通项公式______.
2.(2022·山西)在数列中,若,则________.
3.(2022湖南)若数列满足,,则数列的通项公式________.
拓展1 利用递推公式求通项公式常用的方法(精讲)
考点一 公式法
【例1-1】(2022·青海)已知数列的前项和,则=________.
答案:
【解析】由于数列的前项和.
当时,;
当时,.
满足.因此,对任意的,.故答案为:.
【例1-2】(2023·全国·高三专题练习)已知数列的前n项和,则数列的通项公式为______.
答案:
【解析】因为,
当时,,
当时,,
所以.故答案为:.
【例1-3】(2022·广东)已知正项数列的前项和为,满足.求数列的通项公式 ;
答案:
【解析】①;
当时,代入①得.
当时,②;
①-②得,
整理得,
因为,所以,
所以数列为等差数列,公差为1,
所以.
【例1-4】(2022·北京)已知数列满足,求的通项公式 .
答案:.
【解析】对任意的,,
当时,则,
当时,由,可得,
上述两个等式作差可得,
,
满足,
因此,对任意的,.
【一隅三反】
1.(2022·上海)设数列的前项和为,且.求数列的通项公式 .
答案:
【解析】当时,;
当时,,
;
经检验:满足;
综上所述:.
2.(2022·广西)设数列满足,且,求.
答案:
【解析】当时,,
即,
两边同时除以,
得,
所以数列是常数数列,
所以,
所以.
3.(2023·安徽省舒城中学)若数列是正项数列,且,则_______.
答案:
【解析】数列是正项数列,且所以,即
时
两式相减得,
所以( )当时,适合上式,所以
4.(2022·福建 )已知数列的前n项和为,且满足,则数列的通项公式为______.
答案:
【解析】因为,所以,即.
当时,,
当时,,
显然不满足上式.
所以.
故答案为:.
考点二 累乘法
【例2-1】(2022·江苏)已知数列满足,,则数列的通项公式是
答案:
【解析】因为,
所以,,,,,,
所以,
即,又,所以;
故选:A
【】例2-2(2022·湖南)已知,,则数列的通项公式是
答案:n
【解析】由,得,
即,
则,,,…,,
由累乘法可得,所以,
又,符合上式,所以.
故选:D.
【一隅三反】
1.(2022·全国·高三专题练习)已知数列满足,且,则( )
A. B. C. D.
答案:D
【解析】数列满足,且,
∴,,
∴,,,,
累乘可得:,
可得:.
故选:D﹒
2.(2022·全国·高二)已知数列满足, ,则数列的通项公式为( )
A. B. C. D.
答案:A
【解析】由,得,
即,则,,,…,,
由累乘法可得,所以,
又,符合上式,所以.
故选:A.
3.(2022河北)已知数列的前n项和为,且满足,则数列的通项公式等于___________
答案:
【解析】由得:,当时,,
两式相减得:,化简整理得:,
当时,,即有,解得,因此,,,,
,
而满足上式,所以.故答案为:
考点三 累加法
【例3-1】(2022·黑龙江)已知数列满足,.
(1)求,;
(2)求数列的通项公式.
答案:(1),(2)
【解析】(1),,,.
(2)由得:,
,
又满足,.
【例3-2】(2022·哈尔滨)在数列中,,,则等于( )
A. B.
C. D.
答案:C
【解析】因,则有,
于是得,当时,
,
因此,,显然,满足上式,
所以.
故选:C
【一隅三反】
1.(2022山东)已知在数列的前项之和为,若,则_______.
答案:
【解析】 .
.
2.(2022·云南)已知数列满足,,,求通项公式.
答案:.
【解析】因为,
所以,
所以,
,
,
……,
,
所以,
因为,
所以,
所以,
因为满足上式,
所以.
3.(2021·全国·高二课时练习)设{an}是首项为1的正项数列且-(n+1)-anan+1=0(n∈N*),求an.
答案:an=n(n∈N*)
【解析】-(n+1)-anan+1=0(n∈N*),可得(an+1+an)[nan+1-(n+1)an]=0.
因为{an}是首项为1的正项数列,故an+1+an为正数,
故nan+1-(n+1)an=0,即=,
所以an=a1·=1.
且当时,符合an=n,所以an=n(n∈N*).
综上可知, an=n(n∈N*).
考点四 构造法
【例4-1】(2022·宁夏)已知数列中,,则等于
答案:
【解析】
所以所以数列是一个以2为首项,以4为公比的等比数列,
所以.故选:C
【例4-2】(2022·上海)已知数列满足,且,则数列的通项公式为______.
答案:
【解析】由两边取倒数可得,即.
所以数列是首项为2,公差为3等差数列.
所以,所以.
故答案为:.
【例4-3】(2022·湖北)已知在数列中,,,则______.
答案:
【解析】因为,,所以,
整理得,所以数列是以为首项,
为公比的等比数列,所以,解得.
故答案为:.
【例4-4】(2022·江西)数列{an}满足,,则数列{an}的通项公式为___________.
答案:.
【解析】∵,所以,即,
∴是等差数列,而,
所以,
所以.故答案为:.
【一隅三反】
1.(2022·青海)在数列中,,,则通项公式______.
答案:
【解析】由得:,又,
数列是以为首项,为公比的等比数列,
,则.
故答案为:.
2.(2022·山西)在数列中,若,则________.
答案:
【解析】取倒数得:,
所以数列是首项为1,公差为2的等差数列,
所以,所以.
故答案为:
3.(2022湖南)若数列满足,,则数列的通项公式________.
答案:
【解析】由,可得,设
则,则
所以是以1为首项,3为公比的等比数列.
则,则,所以
故答案为:
