1.1.1 空间向量及其线性运算(1) 学案(含答案)
文档属性
| 名称 | 1.1.1 空间向量及其线性运算(1) 学案(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 230.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-28 12:25:37 | ||
图片预览



文档简介
1.1 空间向量及其运算
1.1.1空间向量及其线性运算(1)
1. 运用类比方法,经历向量及其运算由平面向空间推广的过程.
2. 理解空间向量及相关概念,掌握空间向量的线性运算及其性质,借助图形理解空间向量线性运算及其运算的意义.
3. 理解空间向量共线的充要条件.
活动一 回顾平面向量的相关内容
1. 基本概念:
(1) 向量的定义:
(2) 向量的模:
(3) 零向量、单位向量、平行向量:
(4) 相等向量、共线向量、相反向量:
2. 平面向量a(a≠0)与b共线的充要条件:
3. 平面向量的加法、减法、数乘运算的定义及运算法则:
几何方法 坐标方法 运算性质
向量的加法 (1) 平行四边形法则 (2) 三角形法则
向量的减法 三角形法则
向量的数乘 λa是一个向量,则 (1) |λa|=|λ||a| (2) 若a≠0,则 当λ>0时,λa与a同向; 当λ<0时,λa与a反向; 特别地, 当λ=0时,λa=0; 当a=0时,λa=0
活动二 类比平面向量探究空间向量的概念及运算
1. 空间向量的概念:
(1) 定义:在空间,我们把具有大小和方向的量叫做空间向量.
(2) 长度或模:空间向量的大小.
(3) 表示方法:
①几何表示法:空间向量用有向线段表示;
②字母表示法:用字母a,b,c,…表示;若向量a的起点是A,终点是B,则向量a也可记作,其模记为|a|或 ||.
(4) 几类特殊的空间向量:
名称 定义及表示
零向量 规定长度为0的向量叫做零向量,记为0
单位向量 模为1的向量叫做单位向量
相反向量 与向量a长度相等而方向相反的向量,叫做a的相反向量,记为-a
共线向量 (平行向量) 如果表示若干空间向量的有向线段所在的直线互相平行或重合,那么这些向量叫做共线向量 规定:零向量与任意向量平行,即对任意向量a,都有0∥a.
相等向量 方向相同且模相等的向量叫做相等向量,同向且等长的有向线段表示同一向量或相等向量
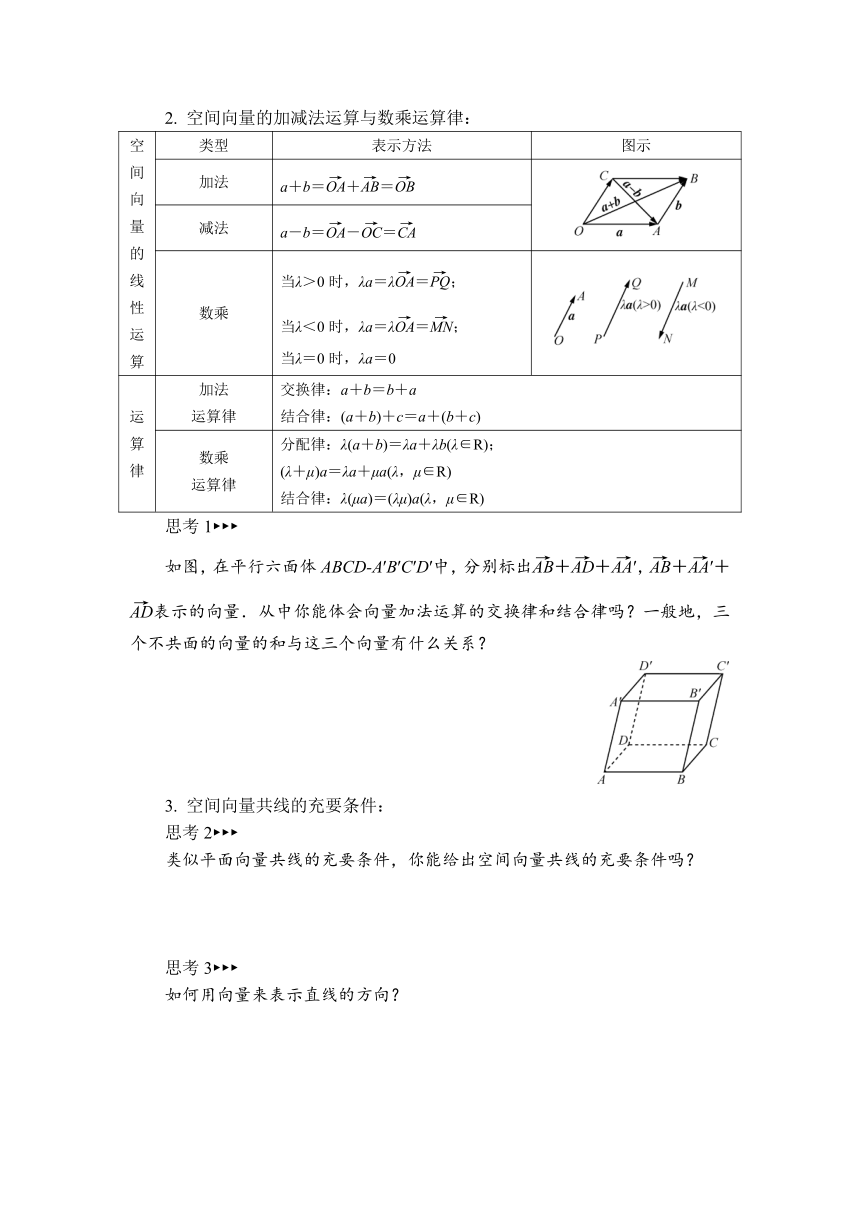
2. 空间向量的加减法运算与数乘运算律:
空间向量的线性运算 类型 表示方法 图示
加法 a+b=+=
减法 a-b=-=
数乘 当λ>0时,λa=λ=; 当λ<0时,λa=λ=; 当λ=0时,λa=0
运算律 加法 运算律 交换律:a+b=b+a 结合律:(a+b)+c=a+(b+c)
数乘 运算律 分配律:λ(a+b)=λa+λb(λ∈R); (λ+μ)a=λa+μa(λ,μ∈R) 结合律:λ(μa)=(λμ)a(λ,μ∈R)
思考1
如图,在平行六面体ABCD-A′B′C′D′中,分别标出++,++表示的向量.从中你能体会向量加法运算的交换律和结合律吗?一般地,三个不共面的向量的和与这三个向量有什么关系?
3. 空间向量共线的充要条件:
思考2
类似平面向量共线的充要条件,你能给出空间向量共线的充要条件吗?
思考3
如何用向量来表示直线的方向?
思考4
除了由两点确定一条直线外,还可以由什么来确定一条直线?
思考5
平面向量与空间向量有哪些相同点与不同点?
活动三 空间向量的运算
例1 如图,在三棱柱ABC-A1B1C1中,M是BB1的中点,化简下列各式,并在图中标出化简得到的向量:
(1) +;
(2) ++;
(3) --.
空间向量加法、减法运算的两个技巧:
(1) 巧用相反向量:向量减法的三角形法则是解决空间向量加法、减法的关键,灵活运用相反向量可使向量首尾相接;
(2) 巧用平移:利用三角形法则和平行四边形法则进行向量加法、减法运算时,务必注意和向量、差向量的方向,必要时可采用空间向量的自由平移获得运算结果.
利用数乘运算进行向量表示的技巧:
(1) 数形结合:利用数乘运算解题时,要结合具体图形,利用向量的三角形法则、平行四边形法则,将目标向量转化为已知向量;
(2) 明确目标:在化简过程中要有目标意识,巧妙运用中点性质.
如图,在长方体ABCD-A1B1C1D1中,下列各式运算结果为的是( )
①--;
②+-;
③--;
④-+.
A. ①② B. ②③ C. ③④ D. ①④
例2 (2023江苏专题练习)已知O,A,B,C,D,E,F,G,H为空间的9个点(如图所示),并且=k,=k,=k,=+m,=+m.求证:AC∥EG.
1. (2023日照阶段练习)下列命题中,为真命题的是( )
A. 向量与的长度相等
B. 将空间中所有的单位向量移到同一个起点,则它们的终点构成一个圆
C. 空间非零向量就是空间中的一条有向线段
D. 不相等的两个空间向量的模必不相等
2. 如图,在三棱锥O-ABC中,M,N分别是AB,OC的中点,设=a,=b,=c,用a,b,c表示,则等于( )
A. (-a+b+c) B. (a+b-c)
C. (a-b+c) D. (-a-b+c)
3. (多选)在正方体ABCD-A1B1C1D1中,已知AC1的中点为O,则下列互为相反向量的是( )
A. +与+
B. -与-
C. -与-
D. +++与+++
4. (2023漯河阶段练习)如图,在三棱柱ABC-A′B′C′中,与是________向量,与是________向量(用“相等”“相反”填空).
5. 如图,在正方体ABCD-A1B1C1D1中,化简下列向量表达式:
(1) +++;
(2) ++.
【参考答案与解析】
【活动方案】
1. (1) 我们把既有大小又有方向的量叫做向量.
(2) 向量的大小称为向量的长度(或称为模).
(3) 长度为0的向量叫做零向量.长度等于1个单位长度的向量叫做单位向量.方向相同或相反的非零向量叫做平行向量.
(4) 长度相等且方向相同的向量叫做相等向量.平行向量也叫做共线向量.我们把与向量a长度相等,方向相反的向量叫做a的相反向量.
2. 存在唯一一个实数λ,使b=λa(a≠0).
3. 填表略
思考1:可以发现,++=++=.一般地, 对于三个不共面的向量a,b,c,以任意点O为起点,a,b,c为邻边作平行六面体,则a,b,c的和等于以O为起点的平行六面体对角线所表示的向量.另外,利用向量加法的交换律和结合律,还可以得到:有限个向量求和,交换相加向量的顺序,其和不变.
思考2:对任意两个空间向量a,b(b≠0),a∥b的充要条件是存在实数λ,使a=λb.
思考3:在直线上任取一个非零向量a,我们把与向量a平行的非零向量都称为该直线的方向向量,则直线的方向向量的方向就可以表示直线的方向.
思考4:直线上一点和它的方向向量确定.
思考5:略
例1 (1) + =.
(2) + + = + =.
(3) - - = - = .
跟踪训练 A ①--=-=;②+-=+=;③--=-=-=≠;④-+=++=+≠.
例2 因为=k,=k,=k,=+m,=+m,所以=-+m(-)=k(-)+km(-)=k+km=k(+m)=k,所以∥.因为AC,EG无公共点,所以AC∥EG.
【检测反馈】
1. A 对于A,因为空间向量与互为相反向量,所以空间向量与的长度相等,故A正确;对于B,将空间中所有的单位向量平移到同一个起点,则它们的终点构成一个球面,故B错误;对于C,空间向量可以用空间中的一条有向线段表示,但空间向量不是有向线段,故C错误;对于D,两个空间向量不相等,它们的模可能相等,也可能不相等,如向量与的模相等,故D错误.
2. B =+=(-)+=-+(-)=+-=(a+b-c).
3. ACD 如图,设M,N分别为AD,B1C1的中点,O1,O2分别为上、下底面的中心. +=2,1+=2,互为相反向量,故A正确; -=,-=,互为相等向量,故B错误;-=,-=,互为相反向量,故C正确;+++=2,+++=2,互为相反向量,故D正确.故选ACD.
4. 相等 相反 在三棱柱ABC-A′B′C′中,四边形ACC′A′是平行四边形,则=,即与是相等向量;四边形ABB′A′是平行四边形,==-,即与是相反向量.
5. (1) +++=+++=++=-=0.
(2) ++=++=.
1.1.1空间向量及其线性运算(1)
1. 运用类比方法,经历向量及其运算由平面向空间推广的过程.
2. 理解空间向量及相关概念,掌握空间向量的线性运算及其性质,借助图形理解空间向量线性运算及其运算的意义.
3. 理解空间向量共线的充要条件.
活动一 回顾平面向量的相关内容
1. 基本概念:
(1) 向量的定义:
(2) 向量的模:
(3) 零向量、单位向量、平行向量:
(4) 相等向量、共线向量、相反向量:
2. 平面向量a(a≠0)与b共线的充要条件:
3. 平面向量的加法、减法、数乘运算的定义及运算法则:
几何方法 坐标方法 运算性质
向量的加法 (1) 平行四边形法则 (2) 三角形法则
向量的减法 三角形法则
向量的数乘 λa是一个向量,则 (1) |λa|=|λ||a| (2) 若a≠0,则 当λ>0时,λa与a同向; 当λ<0时,λa与a反向; 特别地, 当λ=0时,λa=0; 当a=0时,λa=0
活动二 类比平面向量探究空间向量的概念及运算
1. 空间向量的概念:
(1) 定义:在空间,我们把具有大小和方向的量叫做空间向量.
(2) 长度或模:空间向量的大小.
(3) 表示方法:
①几何表示法:空间向量用有向线段表示;
②字母表示法:用字母a,b,c,…表示;若向量a的起点是A,终点是B,则向量a也可记作,其模记为|a|或 ||.
(4) 几类特殊的空间向量:
名称 定义及表示
零向量 规定长度为0的向量叫做零向量,记为0
单位向量 模为1的向量叫做单位向量
相反向量 与向量a长度相等而方向相反的向量,叫做a的相反向量,记为-a
共线向量 (平行向量) 如果表示若干空间向量的有向线段所在的直线互相平行或重合,那么这些向量叫做共线向量 规定:零向量与任意向量平行,即对任意向量a,都有0∥a.
相等向量 方向相同且模相等的向量叫做相等向量,同向且等长的有向线段表示同一向量或相等向量
2. 空间向量的加减法运算与数乘运算律:
空间向量的线性运算 类型 表示方法 图示
加法 a+b=+=
减法 a-b=-=
数乘 当λ>0时,λa=λ=; 当λ<0时,λa=λ=; 当λ=0时,λa=0
运算律 加法 运算律 交换律:a+b=b+a 结合律:(a+b)+c=a+(b+c)
数乘 运算律 分配律:λ(a+b)=λa+λb(λ∈R); (λ+μ)a=λa+μa(λ,μ∈R) 结合律:λ(μa)=(λμ)a(λ,μ∈R)
思考1
如图,在平行六面体ABCD-A′B′C′D′中,分别标出++,++表示的向量.从中你能体会向量加法运算的交换律和结合律吗?一般地,三个不共面的向量的和与这三个向量有什么关系?
3. 空间向量共线的充要条件:
思考2
类似平面向量共线的充要条件,你能给出空间向量共线的充要条件吗?
思考3
如何用向量来表示直线的方向?
思考4
除了由两点确定一条直线外,还可以由什么来确定一条直线?
思考5
平面向量与空间向量有哪些相同点与不同点?
活动三 空间向量的运算
例1 如图,在三棱柱ABC-A1B1C1中,M是BB1的中点,化简下列各式,并在图中标出化简得到的向量:
(1) +;
(2) ++;
(3) --.
空间向量加法、减法运算的两个技巧:
(1) 巧用相反向量:向量减法的三角形法则是解决空间向量加法、减法的关键,灵活运用相反向量可使向量首尾相接;
(2) 巧用平移:利用三角形法则和平行四边形法则进行向量加法、减法运算时,务必注意和向量、差向量的方向,必要时可采用空间向量的自由平移获得运算结果.
利用数乘运算进行向量表示的技巧:
(1) 数形结合:利用数乘运算解题时,要结合具体图形,利用向量的三角形法则、平行四边形法则,将目标向量转化为已知向量;
(2) 明确目标:在化简过程中要有目标意识,巧妙运用中点性质.
如图,在长方体ABCD-A1B1C1D1中,下列各式运算结果为的是( )
①--;
②+-;
③--;
④-+.
A. ①② B. ②③ C. ③④ D. ①④
例2 (2023江苏专题练习)已知O,A,B,C,D,E,F,G,H为空间的9个点(如图所示),并且=k,=k,=k,=+m,=+m.求证:AC∥EG.
1. (2023日照阶段练习)下列命题中,为真命题的是( )
A. 向量与的长度相等
B. 将空间中所有的单位向量移到同一个起点,则它们的终点构成一个圆
C. 空间非零向量就是空间中的一条有向线段
D. 不相等的两个空间向量的模必不相等
2. 如图,在三棱锥O-ABC中,M,N分别是AB,OC的中点,设=a,=b,=c,用a,b,c表示,则等于( )
A. (-a+b+c) B. (a+b-c)
C. (a-b+c) D. (-a-b+c)
3. (多选)在正方体ABCD-A1B1C1D1中,已知AC1的中点为O,则下列互为相反向量的是( )
A. +与+
B. -与-
C. -与-
D. +++与+++
4. (2023漯河阶段练习)如图,在三棱柱ABC-A′B′C′中,与是________向量,与是________向量(用“相等”“相反”填空).
5. 如图,在正方体ABCD-A1B1C1D1中,化简下列向量表达式:
(1) +++;
(2) ++.
【参考答案与解析】
【活动方案】
1. (1) 我们把既有大小又有方向的量叫做向量.
(2) 向量的大小称为向量的长度(或称为模).
(3) 长度为0的向量叫做零向量.长度等于1个单位长度的向量叫做单位向量.方向相同或相反的非零向量叫做平行向量.
(4) 长度相等且方向相同的向量叫做相等向量.平行向量也叫做共线向量.我们把与向量a长度相等,方向相反的向量叫做a的相反向量.
2. 存在唯一一个实数λ,使b=λa(a≠0).
3. 填表略
思考1:可以发现,++=++=.一般地, 对于三个不共面的向量a,b,c,以任意点O为起点,a,b,c为邻边作平行六面体,则a,b,c的和等于以O为起点的平行六面体对角线所表示的向量.另外,利用向量加法的交换律和结合律,还可以得到:有限个向量求和,交换相加向量的顺序,其和不变.
思考2:对任意两个空间向量a,b(b≠0),a∥b的充要条件是存在实数λ,使a=λb.
思考3:在直线上任取一个非零向量a,我们把与向量a平行的非零向量都称为该直线的方向向量,则直线的方向向量的方向就可以表示直线的方向.
思考4:直线上一点和它的方向向量确定.
思考5:略
例1 (1) + =.
(2) + + = + =.
(3) - - = - = .
跟踪训练 A ①--=-=;②+-=+=;③--=-=-=≠;④-+=++=+≠.
例2 因为=k,=k,=k,=+m,=+m,所以=-+m(-)=k(-)+km(-)=k+km=k(+m)=k,所以∥.因为AC,EG无公共点,所以AC∥EG.
【检测反馈】
1. A 对于A,因为空间向量与互为相反向量,所以空间向量与的长度相等,故A正确;对于B,将空间中所有的单位向量平移到同一个起点,则它们的终点构成一个球面,故B错误;对于C,空间向量可以用空间中的一条有向线段表示,但空间向量不是有向线段,故C错误;对于D,两个空间向量不相等,它们的模可能相等,也可能不相等,如向量与的模相等,故D错误.
2. B =+=(-)+=-+(-)=+-=(a+b-c).
3. ACD 如图,设M,N分别为AD,B1C1的中点,O1,O2分别为上、下底面的中心. +=2,1+=2,互为相反向量,故A正确; -=,-=,互为相等向量,故B错误;-=,-=,互为相反向量,故C正确;+++=2,+++=2,互为相反向量,故D正确.故选ACD.
4. 相等 相反 在三棱柱ABC-A′B′C′中,四边形ACC′A′是平行四边形,则=,即与是相等向量;四边形ABB′A′是平行四边形,==-,即与是相反向量.
5. (1) +++=+++=++=-=0.
(2) ++=++=.
