2023-2024学年中考数学重难点冲刺训练(含答案)(长沙地区适用)
文档属性
| 名称 | 2023-2024学年中考数学重难点冲刺训练(含答案)(长沙地区适用) | 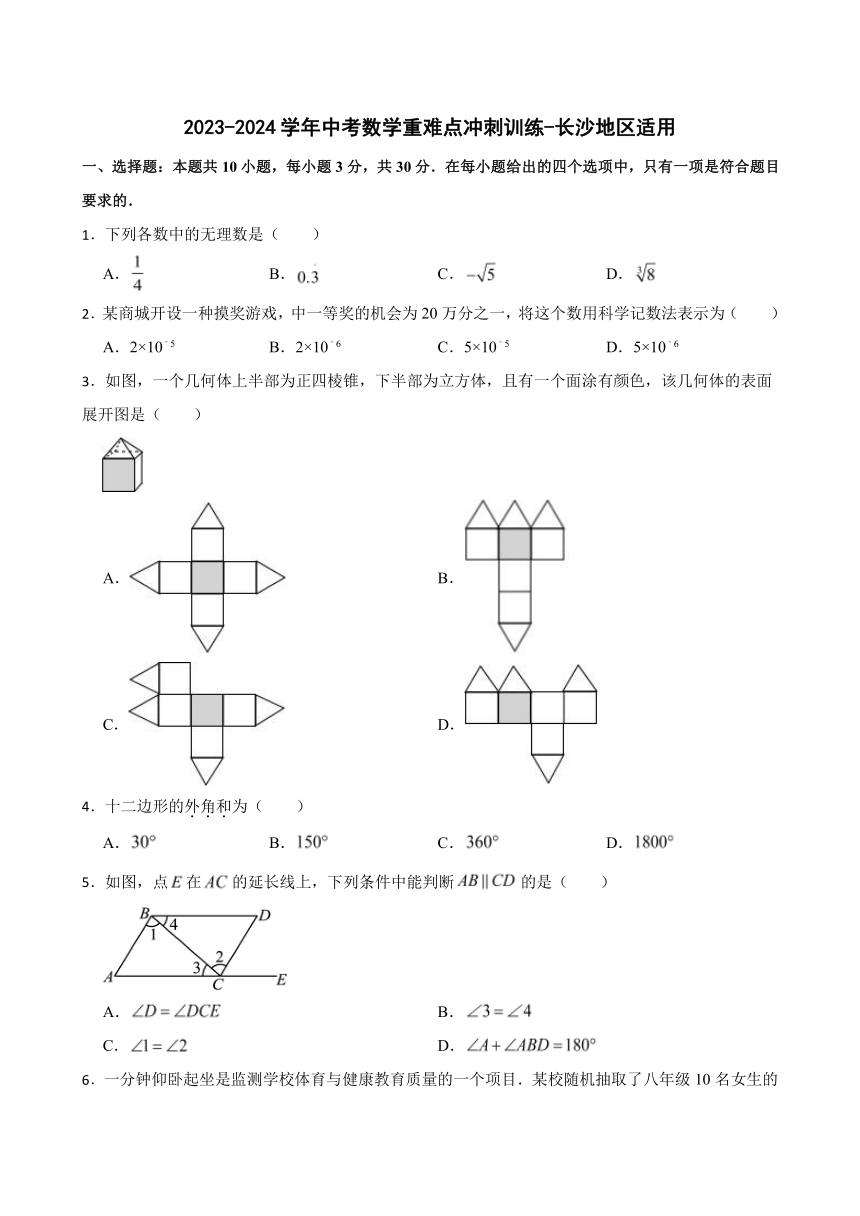 | |
| 格式 | docx | ||
| 文件大小 | 628.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-28 11:11:58 | ||
图片预览





文档简介
2023-2024学年中考数学重难点冲刺训练-长沙地区适用
一、选择题:本题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.下列各数中的无理数是( )
A. B. C. D.
2.某商城开设一种摸奖游戏,中一等奖的机会为20万分之一,将这个数用科学记数法表示为( )
A.2×10﹣5 B.2×10﹣6 C.5×10﹣5 D.5×10﹣6
3.如图,一个几何体上半部为正四棱锥,下半部为立方体,且有一个面涂有颜色,该几何体的表面展开图是( )
A. B.
C. D.
4.十二边形的外角和为( )
A. B. C. D.
5.如图,点在的延长线上,下列条件中能判断的是( )
A. B.
C. D.
6.一分钟仰卧起坐是监测学校体育与健康教育质量的一个项目.某校随机抽取了八年级10名女生的一分钟仰卧起坐测试数据进行统计,分别是40,38,32,34,40,38,45,50,40,45,那么这组数据的众数与中位数分别是( )
A.40,38 B.40,39 C.38,40 D.40,40
7.已知a是一元二次方程的一个根,则代数式的值为( )
A.4 B.8 C. D.
8.世界文化遗产“三孔”景区已经完成5G基站布设,“孔夫子家”自此有了5G 网络.5G网络峰值速率为4G 网络峰值速率的10倍,在峰值速率下传输500兆数据,5G 网络比4G 网络快45秒,求这两种网络的峰值速率.设4G网络的峰值速率为每秒传输 兆数据,依题意,可列方程是( )
A. B.
C. D.
9.我国古代数学名著《九章算术》中记载有这样一道题:“今有二马、一牛价过一万,如半马之价;一马二牛价不满一万,如半牛之价.1问牛、马价各几何?”其大意是:今有2匹马、1头牛的总价超过10000钱,其超出的钱数相当于匹马的价格;1匹马、2头牛的总价不足10000钱,所差的钱数相当于头牛的价格.问每头牛、每匹马的价格各是多少?若设每头牛的价格为x钱,每匹马的价格为y钱,则根据题意列方程组正确的为 ( )
A. B.
C. D.
10.如图所示,小亮设计了一个探究杠杆平衡条件的实验:在一根匀质的木杆中点O左侧固定位置B处悬挂重物A,右侧用一个弹簧测力计向下拉,改变弹簧测力计与支点O的距离,观察弹簧测力计的示数的变化情况.实验数据记录如下表:
…… 10 15 20 25 30 ……
…… 45 30 22.5 18 15 ……
下列说法不正确的是( )
A.弹簧测力计的示数与支点O的距离之间关系的图象如图
B.y与x的函数关系式为
C.当弹簧测力计的示数为时,弹簧测力计与O点的距离是37.5
D.随着弹簧测力计与O点的距离不断增大,弹簧测力计上的示数不断减小
二、填空题:本题共6小题,每小题3分,共18分.
11.因式分解 = .
12.计算: .
13.设、是方程的两个根,且,则 .
14.古希腊一位庄园主把一边长为米的正方形土地租给老农,第二年他对老农说:“我把这块地的一边增加米,相邻的一边减少米,变成长方形土地继续租给你,租金不变”后来老农发现收益减少,感觉吃亏了聪明的你帮老农算出土地面积其实减少了 平方米.
15. 某兴趣小组在探究光沿直线传播时,设计制作了一个由点光源和质地均匀不透光圆环组成的实验装置,由物理学知识,可知点光源发出的光线将圆环的部分区域照亮,其示意图如图所示.已知的半径为,点光源P到圆心O的距离为.现假设可以随意在上取点,则这个点取在无光圆弧部分的概率为 .
16. 如图,在矩形中,,,点E是边上一点,,分别在边上取点M,N,将矩形沿直线翻折,使得点B的对应点恰好落在射线上,点A的对应点是,那么折痕的长为 ;连接,线段的最小值为 .
三、解答题:本题共9小题,共72分,解答应写出文字说明、证明过程或演算步骤.
17.计算
(1)解方程:;
(2)解不等式:.
18. 计算:.
19.如图,在四边形ABCD中,AB∥DC,AB=AD,对角线AC,BD交于点O,AC平分∠BAD,过点C作CE⊥AB交AB的延长线于点E,连接OE.
(1)求证:四边形ABCD是菱形;
(2)若AB=10,BD=8,求OE的长.
20.天坑是喀斯特地貌中的一种,它的形成是因为地下水不断侵蚀固体基岩,使溶洞顶部发生坍塌,最终在地表形成一个巨大的深坑,这个深坑被称作天坑.如图1所示是位于兴文石海具有天下第一漏斗美称的天坑最深处达208米.是天坑坑洞洞口最大口径.现在同一平面内的天坑边沿再另取两点C、D,使.测量示意图如图2所示,在点D处测得,,在点C处测得,,求天坑坑洞洞口最大口径的长度.(结果精确到;参考数据:)
21.如图,在中,,以为直径的交于点P,点Q是线段的中点,连接并延长交的延长线于点D.
(1)求证:直线是的切线;
(2)若,
①求的半径的长;
②求的长.
22.某校化学教学组的老师们在九年级随机抽取了部分学生,就“你最擅长的化学实验是什么”进行了问卷调查,选项为常考的五个实验:A.高锰酸钾制取氧气; B.电解水;C.木炭还原氧化铜; D.一氧化碳还原氧化铜; E.铁的冶炼.要求每个学生必选且只能选择一项,并将调查结果绘制成如下不完整的条形统计图和扇形统计图:
请结合统计图回答下列问题:
(1) 填空: a= , E所对应的扇形圆心角度数是 ;
(2) 请你根据调查结果,估计该校九年级1100名学生中有多少人最擅长的实验是“D.一氧化碳还原氧化铜”
(3) 某堂化学课上,小华学到了这样一个知识:将二氧化碳通入澄清石灰水,澄清石灰水会变浑浊.已知本次调查的五个实验中,C,D,E 三个实验均能产生二氧化碳,若小华从五个实验中任意选做两个,请用列表或画树状图的方法求两个实验所产生的气体均能使澄清石灰水变浑浊的概率.
23. 有一种葡萄:从树上摘下后不保鲜最多只能存放一周,如果放在冷藏室,可以延长保鲜时间,但每天仍有一定数量的葡萄变质,假设保鲜期内的重量基本保持不变,现有一位个体户,按市场价收购了这种葡萄200千克放在冷藏室内,此时市场价为每千克2元,据测算,此后每千克鲜葡萄的市场价格每天可以上涨0.2元,但是,存放一天需各种费用20元,平均每天还有1千克葡萄变质丢弃.
(1)存放x天后将鲜葡萄一次性出售,设鲜葡萄的销售金额为y元,写出y关于x的函数关系式;
(2)为了使鲜葡萄的销售金额为760元,又为了尽早清空冷藏室,则需要在几天后一次性出售完;
(3)问个体户将这批葡萄存放多少天后一次性出售,可获得最大利润 最大利润是多少 (本题不要求写出自变量x的取值范围)
24.如图,在中,,为的中点,点在线段上以点为中心,将线段逆时针旋转得到线段,连接,.
(1)求证:平分;
(2)如图,为的中点,连接试判断与的位置关系,并说明理由;
(3)如图,若,,连接,试说明的面积是一个定值,并求出该定值.
25.抛物线经过点
(1)求这条抛物线的函数解析式.
(2)当时,函数有最大值为5,求的值.
(3)抛物线上有一点,点的横坐标为,另有点,以、为边作矩形,设抛物线的顶点为.
①连结,若的面积是的面积2倍,求的值.
②抛物线的对称轴上有一点,且点的纵坐标为,连接,线段绕点顺时针旋转得线段,以为边作正方形,若正方形与矩形重合部分的图形周长为10,直接写出的值.
答案解析部分
1.【答案】C
2.【答案】D
3.【答案】B
4.【答案】C
5.【答案】C
6.【答案】D
7.【答案】A
8.【答案】A
9.【答案】C
10.【答案】C
11.【答案】
12.【答案】
13.【答案】4
14.【答案】16
15.【答案】
16.【答案】;
17.【答案】(1)解:原方程去分母得:,
解得:,
经检验,是分式方程的解;
(2)解:原不等式移项得:,
合并同类项得:,
系数化为得:.
18.【答案】解:.
.
19.【答案】(1)证明:∵AB∥CD,
∴∠CAB=∠DCA,
∵AC为∠DAB的平分线,
∴∠CAB=∠DAC,
∴∠DCA=∠DAC,
∴CD=AD,
∵AB=AD,
∴AB=CD,
∵AB∥CD,
∴四边形ABCD是平行四边形,
∵AD=AB,
∴平行四边形ABCD是菱形;
(2)解:∵四边形ABCD是菱形,
∴OA=OC,BD⊥AC,
∵CE⊥AB,
∴OE=OA=OC,
∵BD=8,
∴OB=BD=4,
在Rt△AOB 中,AB=10,OB=4,
∴OA===,
∴OE=OA=.
20.【答案】解:如图,过点作延长线于点,
设,
,
,
,,
,
,
,
,,
,
,
,
,
,
,
即天坑坑洞洞口最大口径的长度为米.
21.【答案】(1)证明:连接
是的直径,
,则,
又是的中点,
.
∴,
∵,
∴,
∵,
∴,
∴,即,
∴直线是的切线;
(2)解:①在中,
∵,
∴,
∴,
在中,
∴,
∴的半径长为;
②在中,
∴,
连接,
,
∵是的中点,是的中点,
∴,,,
∵,
∴垂直平分,
∴,
∵,
∴,
∵,
∴,
∴,即,
∵,
∴,
解得:.
22.【答案】(1)50;72°
(2)解:
答:估计该校九年级 1100名学生中有 165人最擅长的实验是“D.一氧化碳还原氧化铜”.
(3)解:根据题意列表如下:
一 A B C D E
A — (A, B) (A, C) (A, D) (A, E)
B (B, A) 一 (B, C) (B, D) (B, E)
C (C, A) (C, B) 一 (C, D) (C, E)
D (D, A) (D, B) (D, C) 一 (D, E)
E (E, A) (E, B) (E, C) (E, D) 一
由表可知,共有20种等可能的结果,其中两个实验所产生的气体均能使澄清石灰水变浑浊的结果有 6种,分别为(C, D), (C, E), (D, C), (D, E), (E, C), (E, D), ∴P(两个实验所产生的气体均能使澄清石灰水变浑浊)
23.【答案】(1)y=(200-x)(0.2x+2)=-0.2x2+38x+400;
(2)当y=760时,-0.2x2+38x+400=760,
解方程得,
∵要尽早清空冷藏室,
所以,
答:要在10天后一次性出售完,可获得销售金额760元;
(3)设利润为w元,
则,
∵-0.2<0,
∴当时,
w有最大值为405.
答:这批葡萄存放45天后一次性出售,可获得最大利润405元.
24.【答案】(1)证明:,
,
即.
在和中,
,
≌,
.
,
,
,
平分;
(2)解:.
证明如下:如图,作,分别交,于点,.
由知.
在和中,
,
≌,
.
又≌,
,
.
点为的中点,
,
.
点为的中点,点为的中点,
,
;
(3)解:,,
为等边三角形,
,
由可知≌,
,
,
,
的面积是一个定值.该定值为
25.【答案】(1)解:把代入中
(2)解:
解得(舍去)或
解得(舍去)或
所以或
(3)解:点坐标为,
解得
解得
所以或
一、选择题:本题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.下列各数中的无理数是( )
A. B. C. D.
2.某商城开设一种摸奖游戏,中一等奖的机会为20万分之一,将这个数用科学记数法表示为( )
A.2×10﹣5 B.2×10﹣6 C.5×10﹣5 D.5×10﹣6
3.如图,一个几何体上半部为正四棱锥,下半部为立方体,且有一个面涂有颜色,该几何体的表面展开图是( )
A. B.
C. D.
4.十二边形的外角和为( )
A. B. C. D.
5.如图,点在的延长线上,下列条件中能判断的是( )
A. B.
C. D.
6.一分钟仰卧起坐是监测学校体育与健康教育质量的一个项目.某校随机抽取了八年级10名女生的一分钟仰卧起坐测试数据进行统计,分别是40,38,32,34,40,38,45,50,40,45,那么这组数据的众数与中位数分别是( )
A.40,38 B.40,39 C.38,40 D.40,40
7.已知a是一元二次方程的一个根,则代数式的值为( )
A.4 B.8 C. D.
8.世界文化遗产“三孔”景区已经完成5G基站布设,“孔夫子家”自此有了5G 网络.5G网络峰值速率为4G 网络峰值速率的10倍,在峰值速率下传输500兆数据,5G 网络比4G 网络快45秒,求这两种网络的峰值速率.设4G网络的峰值速率为每秒传输 兆数据,依题意,可列方程是( )
A. B.
C. D.
9.我国古代数学名著《九章算术》中记载有这样一道题:“今有二马、一牛价过一万,如半马之价;一马二牛价不满一万,如半牛之价.1问牛、马价各几何?”其大意是:今有2匹马、1头牛的总价超过10000钱,其超出的钱数相当于匹马的价格;1匹马、2头牛的总价不足10000钱,所差的钱数相当于头牛的价格.问每头牛、每匹马的价格各是多少?若设每头牛的价格为x钱,每匹马的价格为y钱,则根据题意列方程组正确的为 ( )
A. B.
C. D.
10.如图所示,小亮设计了一个探究杠杆平衡条件的实验:在一根匀质的木杆中点O左侧固定位置B处悬挂重物A,右侧用一个弹簧测力计向下拉,改变弹簧测力计与支点O的距离,观察弹簧测力计的示数的变化情况.实验数据记录如下表:
…… 10 15 20 25 30 ……
…… 45 30 22.5 18 15 ……
下列说法不正确的是( )
A.弹簧测力计的示数与支点O的距离之间关系的图象如图
B.y与x的函数关系式为
C.当弹簧测力计的示数为时,弹簧测力计与O点的距离是37.5
D.随着弹簧测力计与O点的距离不断增大,弹簧测力计上的示数不断减小
二、填空题:本题共6小题,每小题3分,共18分.
11.因式分解 = .
12.计算: .
13.设、是方程的两个根,且,则 .
14.古希腊一位庄园主把一边长为米的正方形土地租给老农,第二年他对老农说:“我把这块地的一边增加米,相邻的一边减少米,变成长方形土地继续租给你,租金不变”后来老农发现收益减少,感觉吃亏了聪明的你帮老农算出土地面积其实减少了 平方米.
15. 某兴趣小组在探究光沿直线传播时,设计制作了一个由点光源和质地均匀不透光圆环组成的实验装置,由物理学知识,可知点光源发出的光线将圆环的部分区域照亮,其示意图如图所示.已知的半径为,点光源P到圆心O的距离为.现假设可以随意在上取点,则这个点取在无光圆弧部分的概率为 .
16. 如图,在矩形中,,,点E是边上一点,,分别在边上取点M,N,将矩形沿直线翻折,使得点B的对应点恰好落在射线上,点A的对应点是,那么折痕的长为 ;连接,线段的最小值为 .
三、解答题:本题共9小题,共72分,解答应写出文字说明、证明过程或演算步骤.
17.计算
(1)解方程:;
(2)解不等式:.
18. 计算:.
19.如图,在四边形ABCD中,AB∥DC,AB=AD,对角线AC,BD交于点O,AC平分∠BAD,过点C作CE⊥AB交AB的延长线于点E,连接OE.
(1)求证:四边形ABCD是菱形;
(2)若AB=10,BD=8,求OE的长.
20.天坑是喀斯特地貌中的一种,它的形成是因为地下水不断侵蚀固体基岩,使溶洞顶部发生坍塌,最终在地表形成一个巨大的深坑,这个深坑被称作天坑.如图1所示是位于兴文石海具有天下第一漏斗美称的天坑最深处达208米.是天坑坑洞洞口最大口径.现在同一平面内的天坑边沿再另取两点C、D,使.测量示意图如图2所示,在点D处测得,,在点C处测得,,求天坑坑洞洞口最大口径的长度.(结果精确到;参考数据:)
21.如图,在中,,以为直径的交于点P,点Q是线段的中点,连接并延长交的延长线于点D.
(1)求证:直线是的切线;
(2)若,
①求的半径的长;
②求的长.
22.某校化学教学组的老师们在九年级随机抽取了部分学生,就“你最擅长的化学实验是什么”进行了问卷调查,选项为常考的五个实验:A.高锰酸钾制取氧气; B.电解水;C.木炭还原氧化铜; D.一氧化碳还原氧化铜; E.铁的冶炼.要求每个学生必选且只能选择一项,并将调查结果绘制成如下不完整的条形统计图和扇形统计图:
请结合统计图回答下列问题:
(1) 填空: a= , E所对应的扇形圆心角度数是 ;
(2) 请你根据调查结果,估计该校九年级1100名学生中有多少人最擅长的实验是“D.一氧化碳还原氧化铜”
(3) 某堂化学课上,小华学到了这样一个知识:将二氧化碳通入澄清石灰水,澄清石灰水会变浑浊.已知本次调查的五个实验中,C,D,E 三个实验均能产生二氧化碳,若小华从五个实验中任意选做两个,请用列表或画树状图的方法求两个实验所产生的气体均能使澄清石灰水变浑浊的概率.
23. 有一种葡萄:从树上摘下后不保鲜最多只能存放一周,如果放在冷藏室,可以延长保鲜时间,但每天仍有一定数量的葡萄变质,假设保鲜期内的重量基本保持不变,现有一位个体户,按市场价收购了这种葡萄200千克放在冷藏室内,此时市场价为每千克2元,据测算,此后每千克鲜葡萄的市场价格每天可以上涨0.2元,但是,存放一天需各种费用20元,平均每天还有1千克葡萄变质丢弃.
(1)存放x天后将鲜葡萄一次性出售,设鲜葡萄的销售金额为y元,写出y关于x的函数关系式;
(2)为了使鲜葡萄的销售金额为760元,又为了尽早清空冷藏室,则需要在几天后一次性出售完;
(3)问个体户将这批葡萄存放多少天后一次性出售,可获得最大利润 最大利润是多少 (本题不要求写出自变量x的取值范围)
24.如图,在中,,为的中点,点在线段上以点为中心,将线段逆时针旋转得到线段,连接,.
(1)求证:平分;
(2)如图,为的中点,连接试判断与的位置关系,并说明理由;
(3)如图,若,,连接,试说明的面积是一个定值,并求出该定值.
25.抛物线经过点
(1)求这条抛物线的函数解析式.
(2)当时,函数有最大值为5,求的值.
(3)抛物线上有一点,点的横坐标为,另有点,以、为边作矩形,设抛物线的顶点为.
①连结,若的面积是的面积2倍,求的值.
②抛物线的对称轴上有一点,且点的纵坐标为,连接,线段绕点顺时针旋转得线段,以为边作正方形,若正方形与矩形重合部分的图形周长为10,直接写出的值.
答案解析部分
1.【答案】C
2.【答案】D
3.【答案】B
4.【答案】C
5.【答案】C
6.【答案】D
7.【答案】A
8.【答案】A
9.【答案】C
10.【答案】C
11.【答案】
12.【答案】
13.【答案】4
14.【答案】16
15.【答案】
16.【答案】;
17.【答案】(1)解:原方程去分母得:,
解得:,
经检验,是分式方程的解;
(2)解:原不等式移项得:,
合并同类项得:,
系数化为得:.
18.【答案】解:.
.
19.【答案】(1)证明:∵AB∥CD,
∴∠CAB=∠DCA,
∵AC为∠DAB的平分线,
∴∠CAB=∠DAC,
∴∠DCA=∠DAC,
∴CD=AD,
∵AB=AD,
∴AB=CD,
∵AB∥CD,
∴四边形ABCD是平行四边形,
∵AD=AB,
∴平行四边形ABCD是菱形;
(2)解:∵四边形ABCD是菱形,
∴OA=OC,BD⊥AC,
∵CE⊥AB,
∴OE=OA=OC,
∵BD=8,
∴OB=BD=4,
在Rt△AOB 中,AB=10,OB=4,
∴OA===,
∴OE=OA=.
20.【答案】解:如图,过点作延长线于点,
设,
,
,
,,
,
,
,
,,
,
,
,
,
,
,
即天坑坑洞洞口最大口径的长度为米.
21.【答案】(1)证明:连接
是的直径,
,则,
又是的中点,
.
∴,
∵,
∴,
∵,
∴,
∴,即,
∴直线是的切线;
(2)解:①在中,
∵,
∴,
∴,
在中,
∴,
∴的半径长为;
②在中,
∴,
连接,
,
∵是的中点,是的中点,
∴,,,
∵,
∴垂直平分,
∴,
∵,
∴,
∵,
∴,
∴,即,
∵,
∴,
解得:.
22.【答案】(1)50;72°
(2)解:
答:估计该校九年级 1100名学生中有 165人最擅长的实验是“D.一氧化碳还原氧化铜”.
(3)解:根据题意列表如下:
一 A B C D E
A — (A, B) (A, C) (A, D) (A, E)
B (B, A) 一 (B, C) (B, D) (B, E)
C (C, A) (C, B) 一 (C, D) (C, E)
D (D, A) (D, B) (D, C) 一 (D, E)
E (E, A) (E, B) (E, C) (E, D) 一
由表可知,共有20种等可能的结果,其中两个实验所产生的气体均能使澄清石灰水变浑浊的结果有 6种,分别为(C, D), (C, E), (D, C), (D, E), (E, C), (E, D), ∴P(两个实验所产生的气体均能使澄清石灰水变浑浊)
23.【答案】(1)y=(200-x)(0.2x+2)=-0.2x2+38x+400;
(2)当y=760时,-0.2x2+38x+400=760,
解方程得,
∵要尽早清空冷藏室,
所以,
答:要在10天后一次性出售完,可获得销售金额760元;
(3)设利润为w元,
则,
∵-0.2<0,
∴当时,
w有最大值为405.
答:这批葡萄存放45天后一次性出售,可获得最大利润405元.
24.【答案】(1)证明:,
,
即.
在和中,
,
≌,
.
,
,
,
平分;
(2)解:.
证明如下:如图,作,分别交,于点,.
由知.
在和中,
,
≌,
.
又≌,
,
.
点为的中点,
,
.
点为的中点,点为的中点,
,
;
(3)解:,,
为等边三角形,
,
由可知≌,
,
,
,
的面积是一个定值.该定值为
25.【答案】(1)解:把代入中
(2)解:
解得(舍去)或
解得(舍去)或
所以或
(3)解:点坐标为,
解得
解得
所以或
同课章节目录
