六年级数学上册人教版《 数学广角——数与形 》课件(16张ppt)
文档属性
| 名称 | 六年级数学上册人教版《 数学广角——数与形 》课件(16张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-28 10:09:55 | ||
图片预览




文档简介
(共16张PPT)
人教版小学数学六年级上册
数学广角-数与形
重点:经理观察、操作、归纳等活动,帮助学生借助“形”来直观感受与“数”之间的关系
难点:体会有时“形”与“数”能互相解释,并能借助“形”解决一些与“数”有关的问题
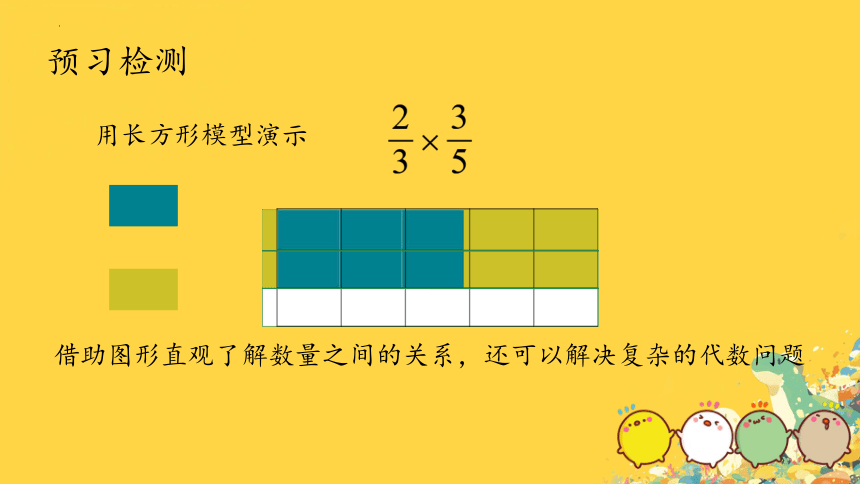
预习检测
用长方形模型演示
借助图形直观了解数量之间的关系,还可以解决复杂的代数问题
?
探究新知
感受数与形之间的联系
每一幅图由几个小正方形组成的?想象一下,下一幅图是什么样子的?
1+3=4
2 = 4
1+3+5=9
3 = 9
1+3+5+7=16
4 =16
1+3+5+7+9=25
5 =25
1+3=2
1+3+5=3
1+3+5+7=4
1+3+5+7+9=5
仔细观察,说一说这些算式有什么特点?
从1开始,几个连续奇数的和等于加数个数的平方
… …
… …
1= 1
1+3= 2
1+3+5= 3
1+3+5+7= 4
1+3+5+7+9= 5
1+3+5+7+9+11 = 6
… …
1+3+5+7+9+11+…… = n
n个
正方形数
1
3
5
7
9
11
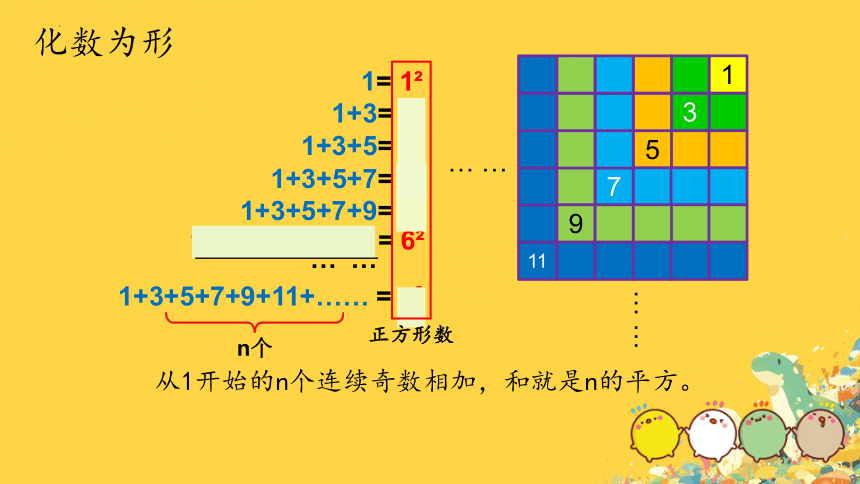
化数为形
从1开始的n个连续奇数相加,和就是n的平方。
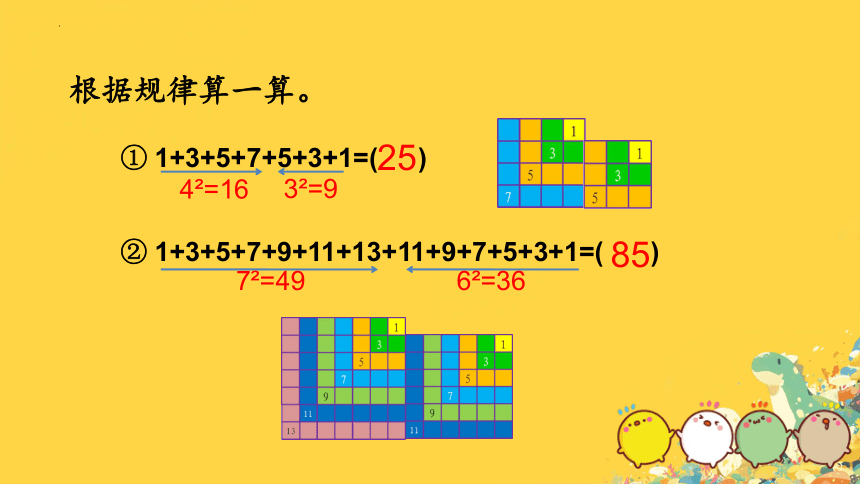
① 1+3+5+7+5+3+1=( )
25
根据规律算一算。
② 1+3+5+7+9+11+13+11+9+7+5+3+1=( )
7 =49
6 =36
85
4 =16
3 =9
自主探究
计算
1.观察算式中加数的特点,你有什么发现?
2.分步算一算,你有什么发现?
从第二个数开始,每个数是前一个数的
数形结合,验证规律
结合正方形的面积验证:用一个正方形的面积表示单位“1”,则原算式可表示为:
结合圆的面积验证:用一个圆的面积表示单位“1”,则原算式可表示为:
数形结合,验证规律
结合线段图验证:用一条线段表示单位“1”,则原算式可表示为:
数形结合,验证规律
数形结合的方法把抽象的代数问题形象化,使其直观,简洁、易懂。
数形结合
无限接近1
巩固练习
利用面积模型解释乘法分配律:
课堂总结
1.从1开始,几个连续奇数的和等于加数个数的平方
2.从1开始,几个连续奇数的和等于加数个数的平方
3.数形结合
无限接近1
布置作业
1.从2起连续偶数的和等于多少?
2.教材108页“做一做”
谢
谢
指
导
人教版小学数学六年级上册
数学广角-数与形
重点:经理观察、操作、归纳等活动,帮助学生借助“形”来直观感受与“数”之间的关系
难点:体会有时“形”与“数”能互相解释,并能借助“形”解决一些与“数”有关的问题
预习检测
用长方形模型演示
借助图形直观了解数量之间的关系,还可以解决复杂的代数问题
?
探究新知
感受数与形之间的联系
每一幅图由几个小正方形组成的?想象一下,下一幅图是什么样子的?
1+3=4
2 = 4
1+3+5=9
3 = 9
1+3+5+7=16
4 =16
1+3+5+7+9=25
5 =25
1+3=2
1+3+5=3
1+3+5+7=4
1+3+5+7+9=5
仔细观察,说一说这些算式有什么特点?
从1开始,几个连续奇数的和等于加数个数的平方
… …
… …
1= 1
1+3= 2
1+3+5= 3
1+3+5+7= 4
1+3+5+7+9= 5
1+3+5+7+9+11 = 6
… …
1+3+5+7+9+11+…… = n
n个
正方形数
1
3
5
7
9
11
化数为形
从1开始的n个连续奇数相加,和就是n的平方。
① 1+3+5+7+5+3+1=( )
25
根据规律算一算。
② 1+3+5+7+9+11+13+11+9+7+5+3+1=( )
7 =49
6 =36
85
4 =16
3 =9
自主探究
计算
1.观察算式中加数的特点,你有什么发现?
2.分步算一算,你有什么发现?
从第二个数开始,每个数是前一个数的
数形结合,验证规律
结合正方形的面积验证:用一个正方形的面积表示单位“1”,则原算式可表示为:
结合圆的面积验证:用一个圆的面积表示单位“1”,则原算式可表示为:
数形结合,验证规律
结合线段图验证:用一条线段表示单位“1”,则原算式可表示为:
数形结合,验证规律
数形结合的方法把抽象的代数问题形象化,使其直观,简洁、易懂。
数形结合
无限接近1
巩固练习
利用面积模型解释乘法分配律:
课堂总结
1.从1开始,几个连续奇数的和等于加数个数的平方
2.从1开始,几个连续奇数的和等于加数个数的平方
3.数形结合
无限接近1
布置作业
1.从2起连续偶数的和等于多少?
2.教材108页“做一做”
谢
谢
指
导
