数学:13.10 轴对称整章水平测试(2)(北京课改版八年级上)
文档属性
| 名称 | 数学:13.10 轴对称整章水平测试(2)(北京课改版八年级上) |
|
|
| 格式 | rar | ||
| 文件大小 | 43.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 京教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-04-09 00:00:00 | ||
图片预览

文档简介
本资料来自于资源最齐全的21世纪教育网www.21cnjy.com
13.10 轴对称整章水平测试(2)
1、 填空题(每题3分,共30分)
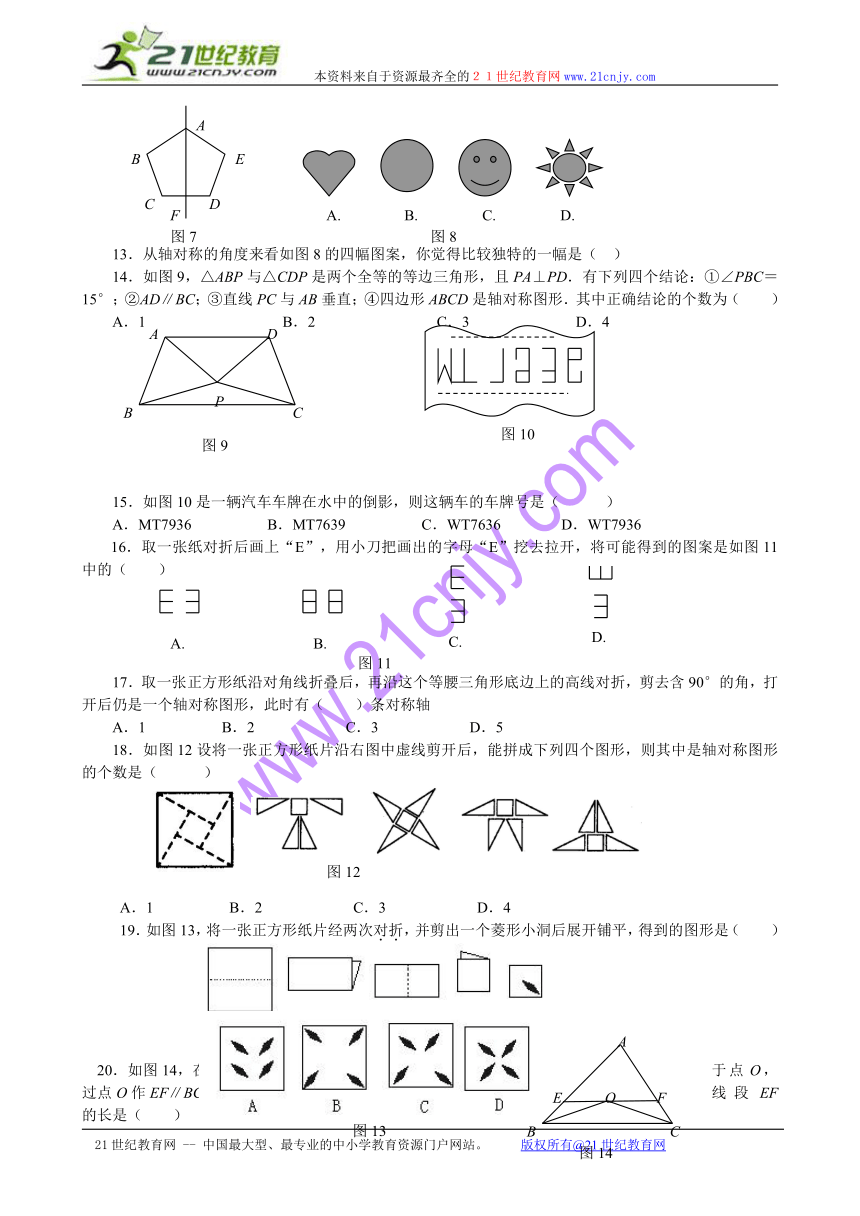
1.五角星是轴对称图形,共有___条对称轴.
2.汉字中如“甲”可以看成是轴对称图形,请你再写出五个___;26个大写英文字母有的可以看成是轴对称图形,请你写出其中的五个___.
3.如图1,BD垂直平分线段AC,AE⊥BC,垂足为E,交BD于P点,PE=3cm,则P点到直线AB的距离是___.
4.已知等腰三角形的顶角是50°,则一腰上的高与底边的夹角等于__度.
5.如果等腰三角形的两条边长分别等于5和6,则它的周长等于___.
6.如图2,在△ABC中,∠BCA=90°,D、E是斜边上的两点,且BD=BC,AE=AC,则∠DCE=___度.
7.若直角三角形斜边上的中线和高分别是5cm,4cm,则这个直角三角形的面积是___cm2.
8.如图3,在等腰梯形ABCD中,AD∥BC,AD=5,AB=6,BC=8,且AB∥DE,则△DEC的周长是___.
9.如图4,在等边△ABC中,AD是高,E是AC上一点,且AE=AD,则∠EDC=_.
10.如图5,在等腰Rt△ABC中,∠C=90°,AC=BC,AD平分∠BAC交BC于D,DE⊥AB于D,若AB=10,则△BDE的周长等于___.
2、 选择题(每题3分,共30分)
11.如图6所示的图形中对称轴最多的图形是( )
12.如图7所示的正五边形中,以AF为对称轴,则图中对应相等的角有( )
A.2对 B.3对 C.4对 D.1对
13.从轴对称的角度来看如图8的四幅图案,你觉得比较独特的一幅是( )
14.如图9,△ABP与△CDP是两个全等的等边三角形,且PA⊥PD.有下列四个结论:①∠PBC=15°;②AD∥BC;③直线PC与AB垂直;④四边形ABCD是轴对称图形.其中正确结论的个数为( )
A.1 B.2 C.3 D.4
15.如图10是一辆汽车车牌在水中的倒影,则这辆车的车牌号是( )
A.MT7936 B.MT7639 C.WT7636 D.WT7936
16.取一张纸对折后画上“E”,用小刀把画出的字母“E”挖去拉开,将可能得到的图案是如图11中的( )
17.取一张正方形纸沿对角线折叠后,再沿这个等腰三角形底边上的高线对折,剪去含90°的角,打开后仍是一个轴对称图形,此时有( )条对称轴
A.1 B.2 C.3 D.5
18.如图12设将一张正方形纸片沿右图中虚线剪开后,能拼成下列四个图形,则其中是轴对称图形的个数是( )
A.1 B.2 C.3 D.4
19.如图13,将一张正方形纸片经两次对折,并剪出一个菱形小洞后展开铺平,得到的图形是( )
20.如图14,在△ABC中,已知∠ABC与∠ACB的平分线交于点O,过点O作EF∥BC交AB于E,交AC于于F,若BE+CF=5,则线段EF的长是( )
A.6 B.5 C.4 D.3
3、 解答题(每小题5分,共40分)
21.(1)以虚线为对称轴画出图15的另一半;(2)画出图16中所有图形的对称轴.
22.尺规作图:把右图17(实线部分)补成以虚线l 为对称轴的轴对称图形,你会得到一只美丽蝴蝶的图案(不用写作法,保留作图痕迹).
23.两个能完全重合的三角板,可以拼出各种不同的图形,图18中已画出其中一个三角形,请你分别补画出另一个与其全等的三角形,使每个图形分别呈不同的轴对称图形,所画三角形与原三角形可以有重叠部分.
24.世界上因为有了圆的图案,万物才显得富有生机,图19来自现实生活的图形中都有圆,它们看上去多么美丽和谐,这正是因为具有对称性,
(1)请问以上三个图形中轴对称图形有___;
(2)请你再画出两个上面图案不重复的图案,要体现对称和美观.
25.如图20的等腰梯形中,两腰都等于1,两底分别等于1和2,请你用不同的方案,在下面3个梯形中各画2条线段,使每一个梯形都被分割成3个轴对称图形.
26.如图21,△ABC和△A′B′C′关于直线MN对称,△A′B′C′和△A″B″C″关于直线EF对称.
(1)画出直线EF;
(2)直线MN与EF相交于点O,试探究∠BOB″与直线MN、EF所夹锐角α的数量关系.
27.如图22,BP、CP是△ABC的外角平分线,则点P必在∠BAC的平分线上,你能说出其中的道理吗?
28.如图23等腰梯形ABCD中,AD∥BC,BA=AD=DC,BD⊥CD,请你求出等腰梯形ABCD各角的度数.
29.如图24,点C为线段AB上一点,△ACM,△CBN是等边三角形,直线AN,MC交于点F.
(1)试说明AN与BM的数量关系,并说出你的理由.
(2)△CEF是等边三角形吗?说出你的依据.
(3)将△ACM绕点C按逆时针方向旋转90°,其他条件不变,在如图25中补出符合要求的图形,并判断第(1)、(2)两小题的结论是否仍然成立(不要求证明).
参考答案:
一、1.5 2.略 3.3 4.25° 5.16或17
6.45° 7.20 8.15 9.10° 10.10.
二、11.C 12.C 13.B 14.D 15.A 16.A 17.B 18.C 19.D 20.B
三、21.略
22.略
23.略
24.(1)三个都是、(2)略
25.略
26.(1)连结B′B″.作线段B′B″的垂直平分线EF. 则直线EF是△A′B′C′和△A″B″C″的对称轴.(2)连结B′O.因为△ABC和△A′B′C′关于MN对称,所以∠BOM=∠B′OM.又△A′B′C′和△A″B″C″关于EF对称,所以∠B′OE=∠B″OE. 所以∠BOB″=∠BOM+∠B′OM+∠B′OE+∠B″OE=2(∠B′OM+∠B′OE)=2α,即∠BOB″=2α.
27.可过点P向三角形的三边引垂线,利用角平分线的性质即得
28.60°、60°、120°、120°
29.(1)AN=BM.理由:△CAN≌△MCB,(2)是.△ACE≌△MCF和∠ECF=60°,(3)略,AN=BM成立,而△CEF不是等边三角形.
图3
E
C
D
B
A
图1
E
C
D
P
A
B
D
图2
B
C
E
A
图5
E
D
C
B
A
E
D
C
B
图4
A
A. B. C. D.
图6
图7
B
F
C
D
A
E
图8
A.
B.
D.
C.
D
图9
C
B
A
P
图10
图11
A.
B.
D.
C.
图12
图13
图14
O
F
E
C
B
A
图17
l
图15
图16
图19
图18
图21
A
N
M
B
C
A′
A″
B′
B″
C′
C″
(3)
(1)
(2)
图20
图22
A
P
B
C
图23
C
A
B
D
图25
B
A
N
M
C
A
图24
B
C
M
N
E
F
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
13.10 轴对称整章水平测试(2)
1、 填空题(每题3分,共30分)
1.五角星是轴对称图形,共有___条对称轴.
2.汉字中如“甲”可以看成是轴对称图形,请你再写出五个___;26个大写英文字母有的可以看成是轴对称图形,请你写出其中的五个___.
3.如图1,BD垂直平分线段AC,AE⊥BC,垂足为E,交BD于P点,PE=3cm,则P点到直线AB的距离是___.
4.已知等腰三角形的顶角是50°,则一腰上的高与底边的夹角等于__度.
5.如果等腰三角形的两条边长分别等于5和6,则它的周长等于___.
6.如图2,在△ABC中,∠BCA=90°,D、E是斜边上的两点,且BD=BC,AE=AC,则∠DCE=___度.
7.若直角三角形斜边上的中线和高分别是5cm,4cm,则这个直角三角形的面积是___cm2.
8.如图3,在等腰梯形ABCD中,AD∥BC,AD=5,AB=6,BC=8,且AB∥DE,则△DEC的周长是___.
9.如图4,在等边△ABC中,AD是高,E是AC上一点,且AE=AD,则∠EDC=_.
10.如图5,在等腰Rt△ABC中,∠C=90°,AC=BC,AD平分∠BAC交BC于D,DE⊥AB于D,若AB=10,则△BDE的周长等于___.
2、 选择题(每题3分,共30分)
11.如图6所示的图形中对称轴最多的图形是( )
12.如图7所示的正五边形中,以AF为对称轴,则图中对应相等的角有( )
A.2对 B.3对 C.4对 D.1对
13.从轴对称的角度来看如图8的四幅图案,你觉得比较独特的一幅是( )
14.如图9,△ABP与△CDP是两个全等的等边三角形,且PA⊥PD.有下列四个结论:①∠PBC=15°;②AD∥BC;③直线PC与AB垂直;④四边形ABCD是轴对称图形.其中正确结论的个数为( )
A.1 B.2 C.3 D.4
15.如图10是一辆汽车车牌在水中的倒影,则这辆车的车牌号是( )
A.MT7936 B.MT7639 C.WT7636 D.WT7936
16.取一张纸对折后画上“E”,用小刀把画出的字母“E”挖去拉开,将可能得到的图案是如图11中的( )
17.取一张正方形纸沿对角线折叠后,再沿这个等腰三角形底边上的高线对折,剪去含90°的角,打开后仍是一个轴对称图形,此时有( )条对称轴
A.1 B.2 C.3 D.5
18.如图12设将一张正方形纸片沿右图中虚线剪开后,能拼成下列四个图形,则其中是轴对称图形的个数是( )
A.1 B.2 C.3 D.4
19.如图13,将一张正方形纸片经两次对折,并剪出一个菱形小洞后展开铺平,得到的图形是( )
20.如图14,在△ABC中,已知∠ABC与∠ACB的平分线交于点O,过点O作EF∥BC交AB于E,交AC于于F,若BE+CF=5,则线段EF的长是( )
A.6 B.5 C.4 D.3
3、 解答题(每小题5分,共40分)
21.(1)以虚线为对称轴画出图15的另一半;(2)画出图16中所有图形的对称轴.
22.尺规作图:把右图17(实线部分)补成以虚线l 为对称轴的轴对称图形,你会得到一只美丽蝴蝶的图案(不用写作法,保留作图痕迹).
23.两个能完全重合的三角板,可以拼出各种不同的图形,图18中已画出其中一个三角形,请你分别补画出另一个与其全等的三角形,使每个图形分别呈不同的轴对称图形,所画三角形与原三角形可以有重叠部分.
24.世界上因为有了圆的图案,万物才显得富有生机,图19来自现实生活的图形中都有圆,它们看上去多么美丽和谐,这正是因为具有对称性,
(1)请问以上三个图形中轴对称图形有___;
(2)请你再画出两个上面图案不重复的图案,要体现对称和美观.
25.如图20的等腰梯形中,两腰都等于1,两底分别等于1和2,请你用不同的方案,在下面3个梯形中各画2条线段,使每一个梯形都被分割成3个轴对称图形.
26.如图21,△ABC和△A′B′C′关于直线MN对称,△A′B′C′和△A″B″C″关于直线EF对称.
(1)画出直线EF;
(2)直线MN与EF相交于点O,试探究∠BOB″与直线MN、EF所夹锐角α的数量关系.
27.如图22,BP、CP是△ABC的外角平分线,则点P必在∠BAC的平分线上,你能说出其中的道理吗?
28.如图23等腰梯形ABCD中,AD∥BC,BA=AD=DC,BD⊥CD,请你求出等腰梯形ABCD各角的度数.
29.如图24,点C为线段AB上一点,△ACM,△CBN是等边三角形,直线AN,MC交于点F.
(1)试说明AN与BM的数量关系,并说出你的理由.
(2)△CEF是等边三角形吗?说出你的依据.
(3)将△ACM绕点C按逆时针方向旋转90°,其他条件不变,在如图25中补出符合要求的图形,并判断第(1)、(2)两小题的结论是否仍然成立(不要求证明).
参考答案:
一、1.5 2.略 3.3 4.25° 5.16或17
6.45° 7.20 8.15 9.10° 10.10.
二、11.C 12.C 13.B 14.D 15.A 16.A 17.B 18.C 19.D 20.B
三、21.略
22.略
23.略
24.(1)三个都是、(2)略
25.略
26.(1)连结B′B″.作线段B′B″的垂直平分线EF. 则直线EF是△A′B′C′和△A″B″C″的对称轴.(2)连结B′O.因为△ABC和△A′B′C′关于MN对称,所以∠BOM=∠B′OM.又△A′B′C′和△A″B″C″关于EF对称,所以∠B′OE=∠B″OE. 所以∠BOB″=∠BOM+∠B′OM+∠B′OE+∠B″OE=2(∠B′OM+∠B′OE)=2α,即∠BOB″=2α.
27.可过点P向三角形的三边引垂线,利用角平分线的性质即得
28.60°、60°、120°、120°
29.(1)AN=BM.理由:△CAN≌△MCB,(2)是.△ACE≌△MCF和∠ECF=60°,(3)略,AN=BM成立,而△CEF不是等边三角形.
图3
E
C
D
B
A
图1
E
C
D
P
A
B
D
图2
B
C
E
A
图5
E
D
C
B
A
E
D
C
B
图4
A
A. B. C. D.
图6
图7
B
F
C
D
A
E
图8
A.
B.
D.
C.
D
图9
C
B
A
P
图10
图11
A.
B.
D.
C.
图12
图13
图14
O
F
E
C
B
A
图17
l
图15
图16
图19
图18
图21
A
N
M
B
C
A′
A″
B′
B″
C′
C″
(3)
(1)
(2)
图20
图22
A
P
B
C
图23
C
A
B
D
图25
B
A
N
M
C
A
图24
B
C
M
N
E
F
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
同课章节目录
- 第十章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的乘除法
- 10.4 分式的加减法
- 10.5 可化为一元一次方程的分式方程及其应用
- 第十一章 实数和二次根式
- 11.1 平方根
- 11.2 立方根
- 11.3 用科学计算器开方
- 11.4 无理数与实数
- 11.5 二次根式及其性质
- 11.6 二次根式的乘除法
- 11.7 二次根式的加减法
- 第十二章 三角形
- 12.1 三角形
- 12.2 三角形的性质
- 12.3 三角形中的主要线段
- 12.4 全等三角形
- 12.5 全等三角形的判定
- 12.6 等腰三角形
- 12.7 直角三角形
- 12.8 基本作图
- 12.9 逆命题 、逆定理
- 12.10 轴对称和轴对称图形
- 12.11 勾股定理
- 12.12 勾股定理的逆定理
- 第十三章 事件与可能性
- 13.1 必然事件与随机事件
- 13.2 随机事件发生的可能性
- 13.3 求简单随机事件发生的可能性的大小
