人教版数学八年级上册14.1.3 积的乘方 课件(共18张PPT)
文档属性
| 名称 | 人教版数学八年级上册14.1.3 积的乘方 课件(共18张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 7.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-28 11:15:55 | ||
图片预览





文档简介
(共18张PPT)
14.1 整式的乘法
14.1.3 积的乘方
R·八年级上册
学习目标
1. 认识积的乘方的推导过程.
2. 知道积的乘方运算法则,并能熟练运用.
问题引入
1.口算:
2.(1)同底数幂的乘法:
(2)幂的乘方:
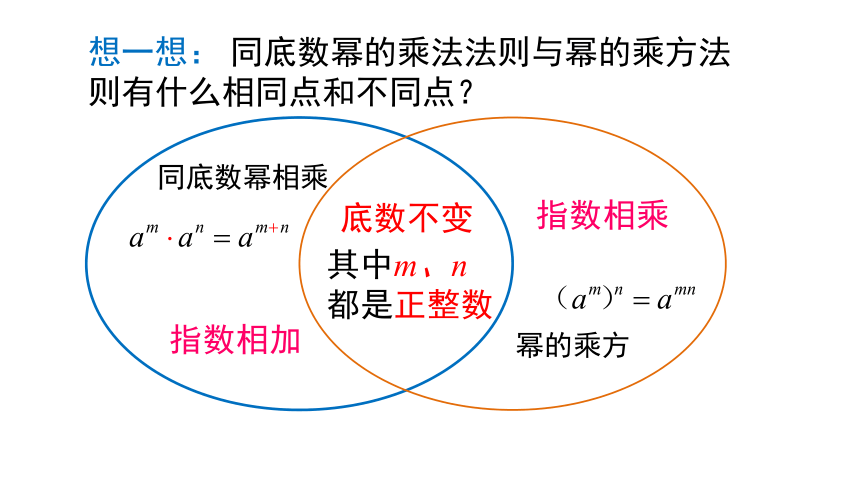
想一想: 同底数幂的乘法法则与幂的乘方法则有什么相同点和不同点?
同底数幂相乘
底数不变
其中m、n都是正整数
幂的乘方
指数相乘
指数相加
新课探究
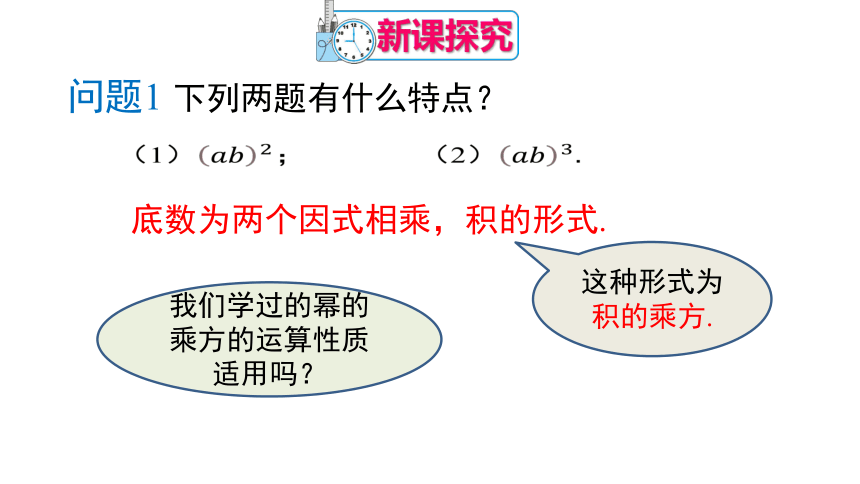
问题1 下列两题有什么特点?
(1);
(2)
底数为两个因式相乘,积的形式.
这种形式为积的乘方.
我们学过的幂的乘方的运算性质适用吗?
问题2 根据乘方的意义、乘法交换律及结合律 进行计算:
(乘方的意义)
(乘法交换律、结合律)
(同底数幂相乘的法则)
同理:
一般地,对于任意底数a、b与任意正整数n,
你能将上面发现的问题规律推导出来吗?
因此,我们有(n为正整数)
即积的乘方,等于把积的每个因式分别乘方,再把所得的幂相乘.
积的乘方法则的推广:
(abc)n=anbncn(n为正整数)
a,b,c可以是任意数,也可以是幂的形式.
积的乘方法则的逆用:
anbn=(ab)n(n为正整数)
想一想:三个或三个以上的积的乘方等于什么?
例3 计算:
(1)(2a)3; (2)(-5b)3;
(3)(xy2)2; (4)(-2x3)4;
=16x12
= x2y4
= -125b3
= 8a3
下面的计算对不对?如果不对,怎样改正?
×
×
×
√
计算:
解:原式
方法总结:逆用积的乘方公式,要灵活运用,对于不符合公式的形式,要通过恒等变形,转化成公式的形式,再运用此公式可进行简便运算.
随堂演练
1.计算(am·an)p= .
amp+np
2. 下列运算正确的是( )
A. x3+x3=x6 B. x·x5=x5
C. (xy)3=x3y3 D. x3·x3=2x6
C
2x3
x6
x6
解析:(am·an)p=amp·anp=amp+np
3. 计算:
(1) (ab)4; (2) (- x y)3;
(3)(-3×10 )3 ; (4)(2ab2)3.
【课本P98 练习】
解:原式
解:原式
解:原式
解:原式
3. 计算:0.1252015×82016
解:原式=0.1252015×82015×8
=(0.125×8)2015×8
=12015×8
=8
4. 解方程:3x+1·2x+1=62x-3
解:3x+1·2x+1=62x-3
即(3×2)x+1=62x-3
x+1=2x-3
x=4
课堂小结
积的乘方
积的乘方,等于把积的每个因式分别乘方,
再把所得的幂相乘.
法则
公式
注意事项
公式中的a,b代表任何代数式·;
每一个因式都要“乘方”;
注意结果的符号、幂指数及其逆向运用(混合运算注意运算顺序).
逆用
1.从课后习题中选取;
2.完成练习册本课时的习题。
课后作业
14.1 整式的乘法
14.1.3 积的乘方
R·八年级上册
学习目标
1. 认识积的乘方的推导过程.
2. 知道积的乘方运算法则,并能熟练运用.
问题引入
1.口算:
2.(1)同底数幂的乘法:
(2)幂的乘方:
想一想: 同底数幂的乘法法则与幂的乘方法则有什么相同点和不同点?
同底数幂相乘
底数不变
其中m、n都是正整数
幂的乘方
指数相乘
指数相加
新课探究
问题1 下列两题有什么特点?
(1);
(2)
底数为两个因式相乘,积的形式.
这种形式为积的乘方.
我们学过的幂的乘方的运算性质适用吗?
问题2 根据乘方的意义、乘法交换律及结合律 进行计算:
(乘方的意义)
(乘法交换律、结合律)
(同底数幂相乘的法则)
同理:
一般地,对于任意底数a、b与任意正整数n,
你能将上面发现的问题规律推导出来吗?
因此,我们有(n为正整数)
即积的乘方,等于把积的每个因式分别乘方,再把所得的幂相乘.
积的乘方法则的推广:
(abc)n=anbncn(n为正整数)
a,b,c可以是任意数,也可以是幂的形式.
积的乘方法则的逆用:
anbn=(ab)n(n为正整数)
想一想:三个或三个以上的积的乘方等于什么?
例3 计算:
(1)(2a)3; (2)(-5b)3;
(3)(xy2)2; (4)(-2x3)4;
=16x12
= x2y4
= -125b3
= 8a3
下面的计算对不对?如果不对,怎样改正?
×
×
×
√
计算:
解:原式
方法总结:逆用积的乘方公式,要灵活运用,对于不符合公式的形式,要通过恒等变形,转化成公式的形式,再运用此公式可进行简便运算.
随堂演练
1.计算(am·an)p= .
amp+np
2. 下列运算正确的是( )
A. x3+x3=x6 B. x·x5=x5
C. (xy)3=x3y3 D. x3·x3=2x6
C
2x3
x6
x6
解析:(am·an)p=amp·anp=amp+np
3. 计算:
(1) (ab)4; (2) (- x y)3;
(3)(-3×10 )3 ; (4)(2ab2)3.
【课本P98 练习】
解:原式
解:原式
解:原式
解:原式
3. 计算:0.1252015×82016
解:原式=0.1252015×82015×8
=(0.125×8)2015×8
=12015×8
=8
4. 解方程:3x+1·2x+1=62x-3
解:3x+1·2x+1=62x-3
即(3×2)x+1=62x-3
x+1=2x-3
x=4
课堂小结
积的乘方
积的乘方,等于把积的每个因式分别乘方,
再把所得的幂相乘.
法则
公式
注意事项
公式中的a,b代表任何代数式·;
每一个因式都要“乘方”;
注意结果的符号、幂指数及其逆向运用(混合运算注意运算顺序).
逆用
1.从课后习题中选取;
2.完成练习册本课时的习题。
课后作业
