人教版数学八年级上册14.3.1 提公因式法 课件(共25张PPT)
文档属性
| 名称 | 人教版数学八年级上册14.3.1 提公因式法 课件(共25张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 16.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-28 00:00:00 | ||
图片预览







文档简介
(共25张PPT)
14.3 因式分解
14.3.1 提公因式法
R·八年级上册
学习目标
1. 了解因式分解的意义.
2. 会用提取公因式法将多项式分解因式.
3. 会利用因式分解进行简便计算.
复习引入
计算:
整式的乘积
多项式
整式的乘积
多项式
根据上面的结果填空:
整式乘法
把一个多项式化成几个整式的积的形式,这样的变形叫做这个多项式的因式分解,也叫把这个多项式分解因式.
想一想:整式乘法与因式分解有什么关系?
整式乘法
因式分解
因式分解的特征:左边是多项式, 右边是几个整式的乘积.
在下列等式中,从左到右的变形是因式分解的有 .
①
②
③
④
⑤
⑥
am+bm+c=m(a+b)+c
12x2y2=3x ·4xy2
x2–4=(x+2)(x–2)
(x+1)2=x2+2x+1
2x+4y+6z=2(x+2y+3z)
a2–b2–1=(a+b)(a–b)–1
×
√
×
×
×
√
③⑥
知识点睛:一个式子的变形是因式分解需同时满足下列条件:①等式左边为多项式;②等式右边为几个整式的积的形式.
下列各式是因式分解的是( ).
强化练习
D
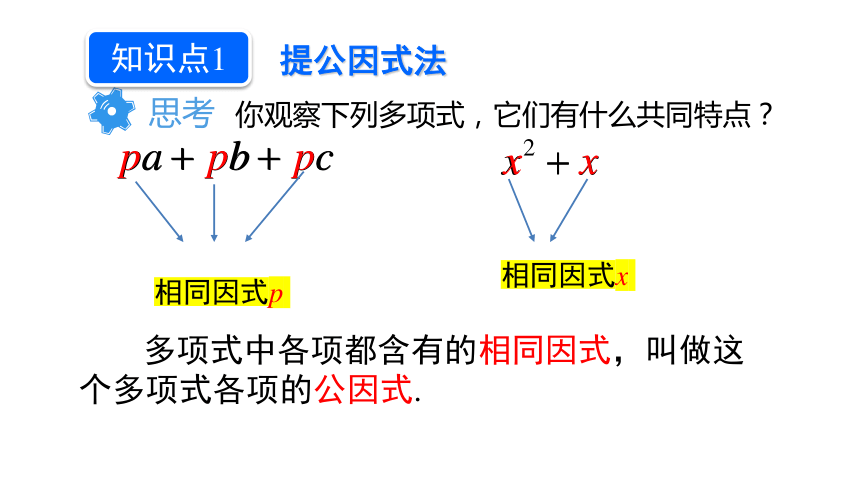
思考 你观察下列多项式,它们有什么共同特点?
提公因式法
知识点1
相同因式p
相同因式x
多项式中各项都含有的相同因式,叫做这个多项式各项的公因式.
一般地,如果多项式的各项有公因式,可以把这个公因式提取出来,将多项式写成公因式与另一个因式的乘积的形式,这种分解因式的方法叫做提公因式法.
如何确定一个多项式的公因式?找下列多项式的公因式.
系数:最大公约数是4
取相同字母a中次数最低的a3
取相同字母b中次数最低的b
多项式的公因式为:4 a3 b
找公因式的步骤:
①
②
③
④
注意:公因式可以是一个数,也可以是单项式或多项式.
找一找:下列各多项式的公因式是多少?
①
②
③
④
⑤
⑥
3x+6y
ab-2ac
a2–a3
4(m+n)2+2(m+n)
9m2n–6mn
–6x2y–8xy2
3
a
a2
2(m+n)
3mn
–2xy
分析:8a3b2+12ab3c中,公因式是 .
提公因式法的应用
知识点2
4ab2
例1 把8a3b2+12ab3c分解因式.
解:
找
提
如果提出公因式4ab,另一个因式是否还有公因式?
判断下列各式因式分解是否正确?如果错误,请改正.
×
注意:首项有负常提负,提负要变号.
×
注意:公因式要提尽.
×
注意:某项提完莫漏1.
分析: 是这两个式子的公因式.
b+c
例2 把2a(b+c)-3(b+c)分解因式.
解:
如何检查因式分解是否正确?
用整式乘法验算
分解因式:
①ax+ay; ②3mx-6my;
③8m2n+2mn; ④12xyz-9x2y2.
=a(x+y)
=3m(x-2y)
强化练习
=2mn(4m+1)
=3xy(4z-3xy)
【课本P115 练习 第1题】
分解因式:
⑤2a(y-z) -3b(z-y);
⑥p(a2+b2)-q(a2+b2) .
强化练习
【课本P115 练习 第1题】
随堂演练
1.下列等式从左到右是因式分解的有( )
(1)x2-x=x(x-1) ; (2)a(a-b)=a2-ab;
(3)a2-9=(a+3)(a-3); (4)a2-2a+1=a(a-2)+1;
A.1个 B.2个 C.3个 D.4个
B
√
√
【课本P115 练习 第2题】
2. 先分解因式,再求值:
4a2(x+7) -3(x+7),其中a=-5,x=3 .
当a=-5,x=3时,
原式=
【课本P115 练习 第3题】
3. 计算5×34+4×34+9×32.
4.简便计算:
5.△ABC的三边长分别为a、b、c,且a+2ab=c+2bc,请判断△ABC是等边三角形、等腰三角形还是直角三角形 并说明理由.
解:整理a+2ab=c+2bc,得:
a+2ab-c-2bc=0.
∴(a-c) +2b(a-c)=0
∴(a-c) (1+2b)=0
∴a-c =0或 1+2b=0
即a=c 或 b=﹣0.5(舍去)
∴△ABC是等腰三角形.
课堂小结
定义
pa+pb+pc=p(a+b+c)
确定公因式的方法:三定.即定系数;定字母;定指数.
1.分解因式是一种恒等变形;
2.公因式:要提尽;
3.不要漏项;
4.提负号,要注意变号.
因式分解
方法
注意
提公因式法
公式法
分两步:找公因式;提公因式.(一找二提)
1.从课后习题中选取;
2.完成练习册本课时的习题。
课后作业
14.3 因式分解
14.3.1 提公因式法
R·八年级上册
学习目标
1. 了解因式分解的意义.
2. 会用提取公因式法将多项式分解因式.
3. 会利用因式分解进行简便计算.
复习引入
计算:
整式的乘积
多项式
整式的乘积
多项式
根据上面的结果填空:
整式乘法
把一个多项式化成几个整式的积的形式,这样的变形叫做这个多项式的因式分解,也叫把这个多项式分解因式.
想一想:整式乘法与因式分解有什么关系?
整式乘法
因式分解
因式分解的特征:左边是多项式, 右边是几个整式的乘积.
在下列等式中,从左到右的变形是因式分解的有 .
①
②
③
④
⑤
⑥
am+bm+c=m(a+b)+c
12x2y2=3x ·4xy2
x2–4=(x+2)(x–2)
(x+1)2=x2+2x+1
2x+4y+6z=2(x+2y+3z)
a2–b2–1=(a+b)(a–b)–1
×
√
×
×
×
√
③⑥
知识点睛:一个式子的变形是因式分解需同时满足下列条件:①等式左边为多项式;②等式右边为几个整式的积的形式.
下列各式是因式分解的是( ).
强化练习
D
思考 你观察下列多项式,它们有什么共同特点?
提公因式法
知识点1
相同因式p
相同因式x
多项式中各项都含有的相同因式,叫做这个多项式各项的公因式.
一般地,如果多项式的各项有公因式,可以把这个公因式提取出来,将多项式写成公因式与另一个因式的乘积的形式,这种分解因式的方法叫做提公因式法.
如何确定一个多项式的公因式?找下列多项式的公因式.
系数:最大公约数是4
取相同字母a中次数最低的a3
取相同字母b中次数最低的b
多项式的公因式为:4 a3 b
找公因式的步骤:
①
②
③
④
注意:公因式可以是一个数,也可以是单项式或多项式.
找一找:下列各多项式的公因式是多少?
①
②
③
④
⑤
⑥
3x+6y
ab-2ac
a2–a3
4(m+n)2+2(m+n)
9m2n–6mn
–6x2y–8xy2
3
a
a2
2(m+n)
3mn
–2xy
分析:8a3b2+12ab3c中,公因式是 .
提公因式法的应用
知识点2
4ab2
例1 把8a3b2+12ab3c分解因式.
解:
找
提
如果提出公因式4ab,另一个因式是否还有公因式?
判断下列各式因式分解是否正确?如果错误,请改正.
×
注意:首项有负常提负,提负要变号.
×
注意:公因式要提尽.
×
注意:某项提完莫漏1.
分析: 是这两个式子的公因式.
b+c
例2 把2a(b+c)-3(b+c)分解因式.
解:
如何检查因式分解是否正确?
用整式乘法验算
分解因式:
①ax+ay; ②3mx-6my;
③8m2n+2mn; ④12xyz-9x2y2.
=a(x+y)
=3m(x-2y)
强化练习
=2mn(4m+1)
=3xy(4z-3xy)
【课本P115 练习 第1题】
分解因式:
⑤2a(y-z) -3b(z-y);
⑥p(a2+b2)-q(a2+b2) .
强化练习
【课本P115 练习 第1题】
随堂演练
1.下列等式从左到右是因式分解的有( )
(1)x2-x=x(x-1) ; (2)a(a-b)=a2-ab;
(3)a2-9=(a+3)(a-3); (4)a2-2a+1=a(a-2)+1;
A.1个 B.2个 C.3个 D.4个
B
√
√
【课本P115 练习 第2题】
2. 先分解因式,再求值:
4a2(x+7) -3(x+7),其中a=-5,x=3 .
当a=-5,x=3时,
原式=
【课本P115 练习 第3题】
3. 计算5×34+4×34+9×32.
4.简便计算:
5.△ABC的三边长分别为a、b、c,且a+2ab=c+2bc,请判断△ABC是等边三角形、等腰三角形还是直角三角形 并说明理由.
解:整理a+2ab=c+2bc,得:
a+2ab-c-2bc=0.
∴(a-c) +2b(a-c)=0
∴(a-c) (1+2b)=0
∴a-c =0或 1+2b=0
即a=c 或 b=﹣0.5(舍去)
∴△ABC是等腰三角形.
课堂小结
定义
pa+pb+pc=p(a+b+c)
确定公因式的方法:三定.即定系数;定字母;定指数.
1.分解因式是一种恒等变形;
2.公因式:要提尽;
3.不要漏项;
4.提负号,要注意变号.
因式分解
方法
注意
提公因式法
公式法
分两步:找公因式;提公因式.(一找二提)
1.从课后习题中选取;
2.完成练习册本课时的习题。
课后作业
