山东省青岛市黄岛区2015-2016学年八年级上学期期中数学试卷【解析版】
文档属性
| 名称 | 山东省青岛市黄岛区2015-2016学年八年级上学期期中数学试卷【解析版】 |  | |
| 格式 | zip | ||
| 文件大小 | 799.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-12-06 10:15:25 | ||
图片预览



文档简介
2015-2016学年山东省青岛市黄岛区八年级(上)期中数学试卷
一、选择题:每小题3分,共24分.
1.下列各数:,,,﹣2,0,1.020020002…(相邻两个2之间0的个数逐次加1),其中无理数有( )
A.1个 B.2个 C.3个 D.4个
2.在平面直角坐标系中,点(﹣3,﹣1)在第( )象限.
A.第一象限 B.第二象限 C.第三象限 D.第四象限
3.下列说法不正确的是( )
A.0的平方根是0
B.一个正数的立方根是一个正数
C.8的算术平方根是4
D.﹣8的立方根是﹣2
4.下列四组线段中,可构成直角三角形的是( )
A.1.5,2,2.5 B.1,2,3 C.1,,3 D.2,3,4
5.下列计算正确的是( )
A.||=2 B.=±7 C.=﹣5 D.=﹣
6.下列函数中,y的值随x值的增大而减小的是( )
①y=8x﹣1;②y=﹣0.6x;③y=x+1;④y=(﹣)x.
A.①② B.③④ C.①③ D.②④
7.计算:(﹣2)2015 (+2)2016=( )
A.+2 B.﹣﹣2 C.﹣2 D.﹣1
8.某校甲、乙两班参加植树活动,乙班先植 ( http: / / www.21cnjy.com )树,然后甲班才开始与乙班一起植树.设甲班植树的总量为y甲(棵),乙班植树的总量为y乙(棵),两班一起植树所用的时间(从甲班开始植树时计时)为x(时),y甲、y乙分别与x之间的部分函数图象如图所示.下列说法正确的有( )
①甲班每小时植树20棵;
②乙班比甲班先植树30棵;
③甲班植树3小时两个班植树总量都是60棵;
④甲班植树超过3小时后,植树总量超过乙班.
( http: / / www.21cnjy.com )
A.1个 B.2个 C.3个 D.4个
二、填空题:每小题3分,共24分.
9.在影剧院里,若将“5排10号”记作(5,10),则(9,3)表示的座位是__________.
10.数轴上到原点距离的点表示的数是__________.
11.10﹣3的立方根是__________.
12.点M(﹣2,1)关于x轴对称的点N的坐标是__________.
13.一次函数y=3x﹣2的图象与坐标轴围成的三角形的面积是__________.
14.满足<x<的整数x是__________.
15.已知(﹣2,y1),(﹣1.5,y2 ( http: / / www.21cnjy.com )),(1,y3)是直线y=2x+b(b为常数)上的三个点,则y1,y2,y3的大小关系是__________.(用“>”表示)
16.图①所示的正方体木块棱长为6cm,沿 ( http: / / www.21cnjy.com )其相邻三个面的对角线(图中虚线)剪掉一角,得到如图②的几何体,一只蚂蚁沿着图②的几何体表面从顶点A爬行到顶点B的最短距离为__________cm.
( http: / / www.21cnjy.com )
三、作图题:6分.
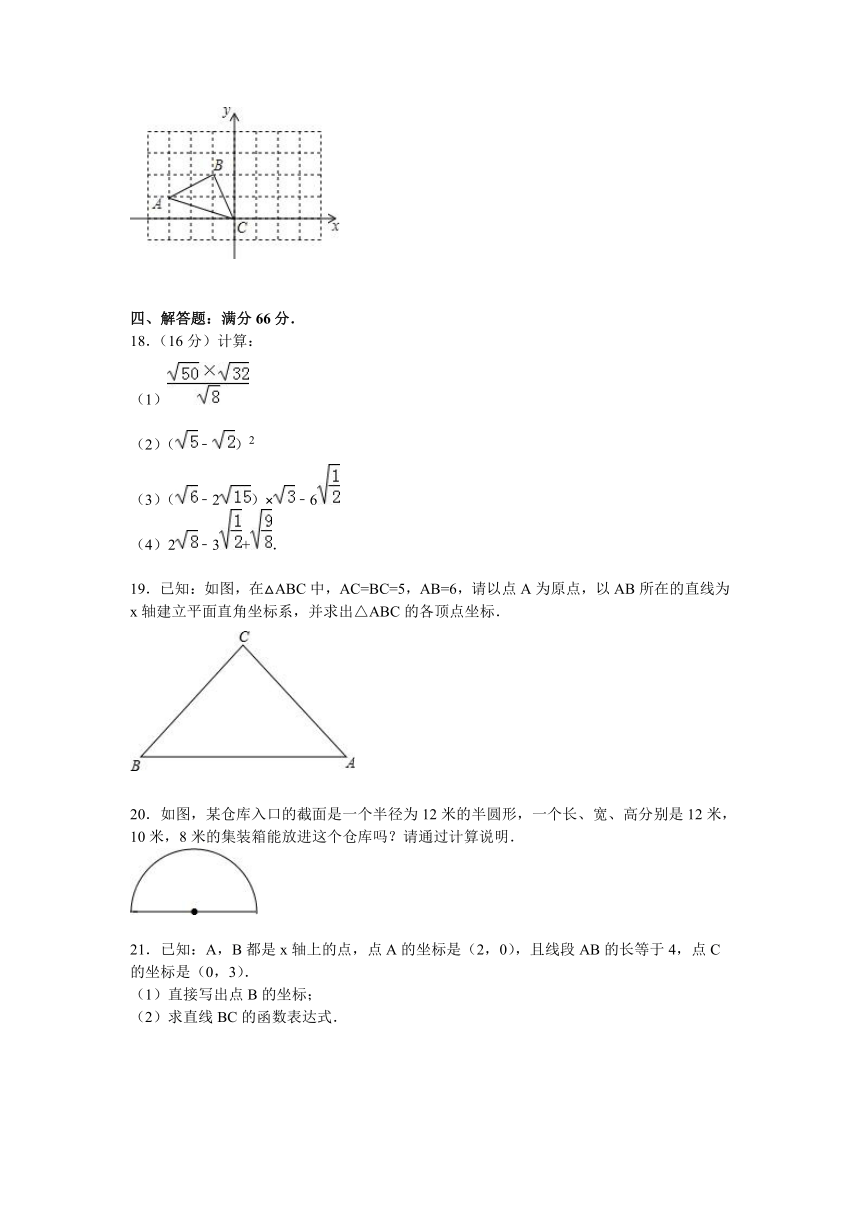
17.如图所示,在方格纸上建立的平面直角坐标系中:
(1)作△ABC关于y轴的对称△A1B1C1.
(2)若线段AB上有点P,坐标为(a,b).则它在A1B1上的对称点P1的坐标为__________.
( http: / / www.21cnjy.com )
四、解答题:满分66分.
18.(16分)计算:
(1)
(2)(﹣)2
(3)(﹣2)×﹣6
(4)2﹣3+.
19.已知:如图,在△AB ( http: / / www.21cnjy.com )C中,AC=BC=5,AB=6,请以点A为原点,以AB所在的直线为x轴建立平面直角坐标系,并求出△ABC的各顶点坐标.
( http: / / www.21cnjy.com )
20.如图,某仓库入口的截面是一个半径为12米的半圆形,一个长、宽、高分别是12米,10米,8米的集装箱能放进这个仓库吗?请通过计算说明.
21.已知:A,B都是x轴上的点,点A的坐标是(2,0),且线段AB的长等于4,点C的坐标是(0,3).
(1)直接写出点B的坐标;
(2)求直线BC的函数表达式.
( http: / / www.21cnjy.com )
22.在进行二次根式运算时,经常会遇到类似,的式子,其实我们还可以将其进一步变形:==;===﹣1.
以上这种将分母变为有理式的恒等变形叫做分母有理化.
再如:===﹣
===﹣2
依照上述方法解答下列问题:
(1)填空:=__________;=__________;=__________.
(2)化简求值:+++…+(写出解答过程)
23.问题提出:求边长分别为,,(a为正整数)三角形的面积.
问题探究:为解决上述数学问题,我们采取数形结合和转化的思想方法,并采取一般问题特殊化的策略来进行探究.
探究一:当a=1时,求边长分别为、、三角形的面积.
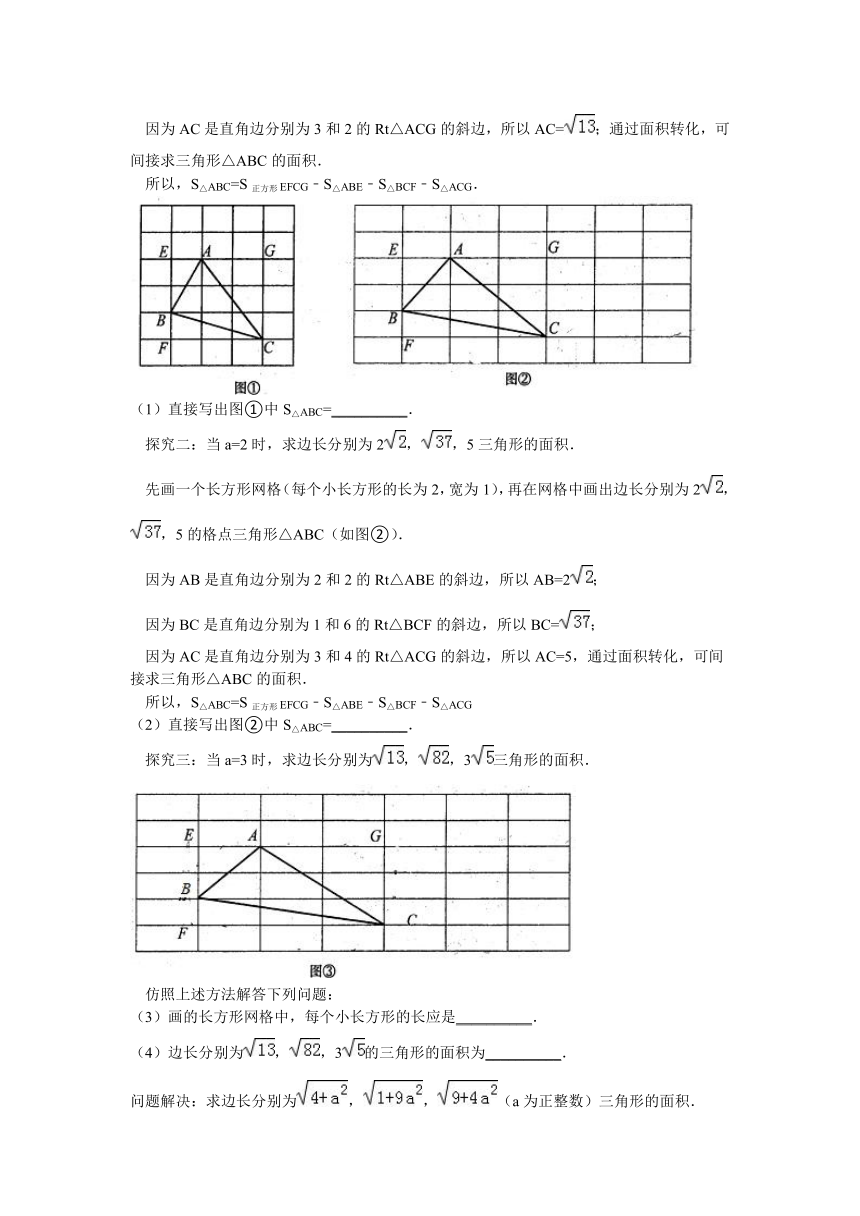
先画一个正方形网格(每个小正方形的边长为1),再在网格中画出边长分别为,,的格点三角形△ABC(如图①).
因为AB是直角边分别为2和1的Rt△ABE的斜边,所以AB=;
因为BC是直角边分别为1和3的Rt△BCF的斜边,所以BC=;
因为AC是直角边分别为3和2的Rt△ACG的斜边,所以AC=;通过面积转化,可间接求三角形△ABC的面积.
所以,S△ABC=S正方形EFCG﹣S△ABE﹣S△BCF﹣S△ACG.
( http: / / www.21cnjy.com )
(1)直接写出图①中S△ABC=__________.
探究二:当a=2时,求边长分别为2,,5三角形的面积.
先画一个长方形网格(每个小长方形的长为2,宽为1),再在网格中画出边长分别为2,,5的格点三角形△ABC(如图②).
因为AB是直角边分别为2和2的Rt△ABE的斜边,所以AB=2;
因为BC是直角边分别为1和6的Rt△BCF的斜边,所以BC=;
因为AC是直角边分别为3和4的Rt△ACG的斜边,所以AC=5,通过面积转化,可间接求三角形△ABC的面积.
所以,S△ABC=S正方形EFCG﹣S△ABE﹣S△BCF﹣S△ACG
(2)直接写出图②中S△ABC=__________.
探究三:当a=3时,求边长分别为,,3三角形的面积.
( http: / / www.21cnjy.com )
仿照上述方法解答下列问题:
(3)画的长方形网格中,每个小长方形的长应是__________.
(4)边长分别为,,3的三角形的面积为__________.
问题解决:求边长分别为,,(a为正整数)三角形的面积.
(5)类比上述方法画长方形网格,每个小长方形的长应是__________.
(6)边长分别为,,(a为正整数)的三角形的面积是__________.
24.在创建国家卫生城市环境综合整治行 ( http: / / www.21cnjy.com )动中,某小区计划对楼体外墙进行粉刷,现有甲、乙两家装饰公司有意承接此项工程.已知甲公司的费用y(元)与粉刷面积x(x≥100)(m2)的关系如表:
粉刷面积x(m2) 100 200 300 400 …
费用y(元) 2000 4000 6000 8000 …
乙公司表示:若该小区先支付3000元的基本承包费,则可按15元/m2的价格收费.请根据以上信息,解答下列问题:
(1)若甲公司收取的费用y(元)与粉刷面积x(m2)满足我们学过某一函数关系,试确定这一函数关系式;
(2)试确定乙公司收取的费用y(元)与粉刷面积x(x≥100)(m2)满足的函数关系式;
(3)在给出的平面直角坐标系内画出(1)(2)中的函数图象,并确定若该小区粉刷面积约为800m2,则选择哪家装饰公司进行施工更合算?
( http: / / www.21cnjy.com )
2015-2016学年山东省青岛市黄岛区八年级(上)期中数学试卷
一、选择题:每小题3分,共24分.
1.下列各数:,,,﹣2,0,1.020020002…(相邻两个2之间0的个数逐次加1),其中无理数有( )
A.1个 B.2个 C.3个 D.4个
【考点】无理数.
【分析】根据无理数的三种形式求解.
【解答】解:=2,=2,
无理数有:,1.020020002…,共2个.
故选B.
【点评】本题考查了无理数的知识,解答本题的关键是掌握无理数的三种形式:①开方开不尽的数,②无限不循环小数,③含有π的数.
2.在平面直角坐标系中,点(﹣3,﹣1)在第( )象限.
A.第一象限 B.第二象限 C.第三象限 D.第四象限
【考点】点的坐标.
【专题】数形结合.
【分析】根据所给点的横纵坐标的符号可得所在象限.
【解答】解:∵所给点的横坐标是﹣3为负数,纵坐标是﹣1为负数,
∴点(﹣3,﹣1)在第三象限,
故选C.
【点评】考查象限内点的符号特点;用到的知识点为:符号为(﹣,﹣)的点在第三象限.
3.下列说法不正确的是( )
A.0的平方根是0
B.一个正数的立方根是一个正数
C.8的算术平方根是4
D.﹣8的立方根是﹣2
【考点】立方根;平方根;算术平方根.
【专题】计算题.
【分析】原式各选项利用平方根,算术平方根,以及立方根定义判断即可.
【解答】解:A、0的平方根是0,正确;
B、一个正数的立方根是一个正数,正确;
C、8的算术平方根是2,错误;
D、﹣8的立方根是﹣2,正确,
故选C
【点评】此题考查了立方根,平方根,以及算术平方根,熟练掌握各自的定义是解本题的关键.
4.下列四组线段中,可构成直角三角形的是( )
A.1.5,2,2.5 B.1,2,3 C.1,,3 D.2,3,4
【考点】勾股定理的逆定理.
【分析】根据勾股定理的逆定理对各选项进行逐一分析即可.
【解答】解:A、∵1.52+22=6.25=2.52,∴能够成直角三角形,故本选项正确;
B、∵1+2=3,∴不能构成三角形,故本选项错误;
C、∵1+<3,不能构成三角形,故本选项错误;
D、∵22+32=13≠42,∴不能够成直角三角形,故本选项错误.
故选A.
【点评】本题考查的是勾股定理的逆定理,熟知如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形就是直角三角形是解答此题的关键.
5.下列计算正确的是( )
A.||=2 B.=±7 C.=﹣5 D.=﹣
【考点】立方根;算术平方根.
【分析】根据算术平方根、立方根的定义,即可解答.
【解答】解:A、||=﹣,故错误;
B、=7,故错误;
C、=5,故错误;
D、,正确.
故选:D.
【点评】本题考查了算术平方根、立方根,解决本题的关键是熟记算术平方根、立方根的定义.
6.下列函数中,y的值随x值的增大而减小的是( )
①y=8x﹣1;②y=﹣0.6x;③y=x+1;④y=(﹣)x.
A.①② B.③④ C.①③ D.②④
【考点】一次函数的性质;正比例函数的性质.
【分析】根据一次函数的性质对各小题进行逐一分析即可.
【解答】解:①∵y=8x﹣1中,k=8>0,∴y的值随x值的增大而增大,故本小题错误;
②∵y=﹣0.6x中,k=﹣0.6<0,∴y的值随x值的增大而减小,故本小题正确;
③∵y=x+1中,k=>0,∴y的值随x值的增大而增大,故本小题错误;
④∵y=(﹣)x中,k=﹣<0,∴y的值随x值的增大而减小,故本小题正确.
故选D.
【点评】本题考查的是一次函数的性质,熟知一次函数的增减性与系数k的关系是解答此题的关键.
7.计算:(﹣2)2015 (+2)2016=( )
A.+2 B.﹣﹣2 C.﹣2 D.﹣1
【考点】二次根式的混合运算.
【分析】逆用积的乘方公式即可求解.
【解答】解:原式=【(﹣2)(+2)】2015(+2)=(﹣1)2015(+2)=﹣(+2)=﹣﹣2.
故选B.
【点评】本题考查了二次根式的运算,逆用积的乘方公式把已知的式子变形成【(﹣2)(+2)】2015(+2)的形式是关键.
8.某校甲、乙两班参加植树活动,乙 ( http: / / www.21cnjy.com )班先植树,然后甲班才开始与乙班一起植树.设甲班植树的总量为y甲(棵),乙班植树的总量为y乙(棵),两班一起植树所用的时间(从甲班开始植树时计时)为x(时),y甲、y乙分别与x之间的部分函数图象如图所示.下列说法正确的有( )
①甲班每小时植树20棵;
②乙班比甲班先植树30棵;
③甲班植树3小时两个班植树总量都是60棵;
④甲班植树超过3小时后,植树总量超过乙班.
( http: / / www.21cnjy.com )
A.1个 B.2个 C.3个 D.4个
【考点】一次函数的应用.
【分析】由图可知:甲班6小时植树1 ( http: / / www.21cnjy.com )20棵,所以甲班每小时植树120÷6=20(棵);甲班开始植树时乙班已经先植树30棵;甲班植树3小时两个班植树总量相等,根据甲班植树的速度可知此时植树的数量;当x>3时,y甲>y乙,即可判断甲班植树超过3小时后,植树总量超过乙班.
【解答】解:由图可知:甲班6小时植树120棵,所以甲班每小时植树120÷6=20(棵),故①正确;
由图象可知:甲班开始植树时乙班已经先植树30棵;故②正确;
由图象可知:甲班植树3小时两个班植树总量相等,根据甲班植树的速度可知此时植树的数为20×3=609棵),故③正确;
由图象可知,当x>3时,y甲在y乙的上方,则甲班植树超过3小时后,植树总量超过乙班,故④正确.
故选:D.
【点评】此题主要考查了一次函数的应用,读懂图,获取正确信息是解题关键.
二、填空题:每小题3分,共24分.
9.在影剧院里,若将“5排10号”记作(5,10),则(9,3)表示的座位是9排3号.
【考点】坐标确定位置.
【分析】根据有序数对(排,号),可得答案.
【解答】解:在影剧院里,若将“5排10号”记作(5,10),则(9,3)表示的座位是9排3号.
故答案为:9排3号.
【点评】本题考查了坐标确定位置,利用(排,号)有序数对表示位置是解题关键.
10.数轴上到原点距离的点表示的数是±.
【考点】实数与数轴.
【分析】根据绝对值的几何意义:一个数的绝对值就是在数轴上表示这个数的点到原点的距离,可知本题就是求绝对值为的数.
【解答】解:根据绝对值的几何意义,得数轴上到原点的距离为的点表示的数,即绝对值为的数,为±.
故答案为±.
【点评】本题考查实数与数轴,绝对值的几何意义.要知道,实数与数轴上的点是一一对应的,互为相反数的两个数到原点的距离相等.
11.10﹣3的立方根是0.1.
【考点】立方根.
【分析】先化简10﹣3=0.001,根据立方根的定义即可解答.
【解答】解:10﹣3=0.001,0.001的立方根为0.1,
故答案为:0.1.
【点评】本题考查了立方根,解决本题的关键是熟记立方根的定义.
12.点M(﹣2,1)关于x轴对称的点N的坐标是N(﹣2,﹣1).
【考点】关于x轴、y轴对称的点的坐标.
【专题】计算题.
【分析】本题比较容易,考查平面直角坐标系中任 ( http: / / www.21cnjy.com )意一点P(x,y),关于x轴对称的点的坐标是(x,﹣y),即横坐标相等,纵坐标互为相反数;据此可得答案.
【解答】解:根据题意,M与N关于x轴对称,
则其横坐标相等,纵坐标互为相反数;
所以N点坐标是(﹣2,﹣1).
故答案为:(﹣2,﹣1).
【点评】本题考查关于x轴对称的两点的坐标之间的关系,关键是掌握两点关于x轴对称则横坐标相等,纵坐标互为相反数.
13.一次函数y=3x﹣2的图象与坐标轴围成的三角形的面积是.
【考点】一次函数图象上点的坐标特征.
【分析】先根据坐标轴上点的坐标特征求出直线与坐标轴的交点坐标,然后根据三角形面积公式求解.
【解答】解:当x=0时,y=3x﹣2=﹣2,则直线与y轴的交点坐标为(0,﹣2);
当y=0时,3x﹣2=0,解得x=,则直线与x轴的交点坐标为(,0),
所以函数y=3x﹣2的图象与坐标轴围成的三角形面积=×2×=.
故答案为.
【点评】本题考查了一次函数图象上点的坐标特征:直线上任意一点的坐标都满足函数关系式y=kx+b.
14.满足<x<的整数x是﹣1,0,1,2.
【考点】估算无理数的大小.
【分析】求出﹣,的范围,即可得出答案.
【解答】解:∵﹣2<﹣<﹣1,2<<3,
∴满足<x<的整数x有﹣1,0,1,2,
故答案为:﹣1,0,1,2.
【点评】本题考查了估算无理数的大小的应用,关键是确定﹣,的范围.
15.已知(﹣2,y1), ( http: / / www.21cnjy.com )(﹣1.5,y2),(1,y3)是直线y=2x+b(b为常数)上的三个点,则y1,y2,y3的大小关系是y3>y2>y1.(用“>”表示)
【考点】一次函数图象上点的坐标特征.
【分析】由y=2x+b(b为常数)可知k=2>0,故y随x的增大而增大,由﹣2<﹣1.5<1,可得y1,y2,y3的大小关系.
【解答】解:∵k=2>0,
∴y随x的增大而增大,
∵﹣2<﹣1.5<1,
∵y3>y2>y1,
故答案为:y3>y2>y1.
【点评】本题主要考查一次函数的增减性,熟练掌握一次函数的增减性是解题的关键.
16.图①所示的正方体木块棱长为6cm,沿其相邻三个面的对角线(图中虚线)剪掉一角,得到如图②的几何体,一只蚂蚁沿着图②的几何体表面从顶点A爬行到顶点B的最短距离为(3+3)cm.
( http: / / www.21cnjy.com )
【考点】平面展开-最短路径问题;截一个几何体.
【专题】压轴题;数形结合.
【分析】要求蚂蚁爬行的最短距离,需将图②的几何体表面展开,进而根据“两点之间线段最短”得出结果.
【解答】解:如图所示:
( http: / / www.21cnjy.com )
△BCD是等腰直角三角形,△ACD是等边三角形,
在Rt△BCD中,CD==6cm,
∴BE=CD=3cm,
在Rt△ACE中,AE==3cm,
∴从顶点A爬行到顶点B的最短距离为(3+3)cm.
故答案为:(3+3).
【点评】考查了平面展开﹣最短路径问题,本题就是把图②的几何体表面展开成平面图形,根据等腰直角三角形的性质和等边三角形的性质解决问题.
三、作图题:6分.
17.如图所示,在方格纸上建立的平面直角坐标系中:
(1)作△ABC关于y轴的对称△A1B1C1.
(2)若线段AB上有点P,坐标为(a,b).则它在A1B1上的对称点P1的坐标为(﹣a,b).
( http: / / www.21cnjy.com )
【考点】作图-轴对称变换.
【分析】(1)作出各点关于y轴的对称点,再顺次连接各点即可;
(2)根据关于y轴对称的点的坐标特点即可得出结论.
【解答】解:(1)如图所示;
(2)∵P(a,b),
∴P1(﹣a,b).
故答案为:(﹣a,b).
( http: / / www.21cnjy.com )
【点评】本题考查的是作图﹣轴对称变换,熟知关于y轴对称的点的坐标特点是解答此题的关键.
四、解答题:满分66分.
18.(16分)计算:
(1)
(2)(﹣)2
(3)(﹣2)×﹣6
(4)2﹣3+.
【考点】二次根式的混合运算.
【分析】(1)首先化简二次根式,然后进行乘除运算即可;
(2)利用完全平方公式计算即可;
(3)首先利用分配律计算乘法,化简二次根式,然后合并同类二次根式即可;
(4)首先化简二次根式,然后合并同类二次根式即可.
【解答】解:(1)原式==10;
(2)原式=5+2﹣2=7﹣2;
(3)原式=﹣2﹣3=3﹣6﹣3=﹣6;
(4)原式=4﹣+=4.
【点评】本题考查的是二次根式的混合运算,在进行此类运算时,一般先把二次根式化为最简二次根式的形式后再运算.
19.已知:如图,在△A ( http: / / www.21cnjy.com )BC中,AC=BC=5,AB=6,请以点A为原点,以AB所在的直线为x轴建立平面直角坐标系,并求出△ABC的各顶点坐标.
( http: / / www.21cnjy.com )
【考点】坐标与图形性质.
【分析】以点A为原点,以AB所在的直线为x轴建立平面直角坐标系,然后过点C作AD⊥AB于D,根据等腰三角形三线合一的性质可得BD=AD=AB,再利用勾股定理列式求出CD,然后写出各点的坐标即可
【解答】解:坐标系如图,
( http: / / www.21cnjy.com )
过点C作CD⊥AB于D,
∵AB=AC=13,BC=10,
∴BD=AD=AB=×6=3,
由勾股定理得,CD===4.
∴A(0,0),B(﹣6,0),C(﹣3,4).
【点评】此题考查坐标与图形的性质,等腰三角形三线合一的性质,勾股定理的应用,作底边上的高,构造出直角三角形并利用性质是解题的关键.
20.如图,某仓库入口的截面是一个半径为12米的半圆形,一个长、宽、高分别是12米,10米,8米的集装箱能放进这个仓库吗?请通过计算说明.
【考点】勾股定理的应用.
【分析】设ABCD是矩形,作OE⊥AB与E,首先根据垂径定理求得AE=5米,然后根据勾股定理求得OE的长,再与箱子的高比较即可判定.
【解答】解:如图,设ABCD是矩形,则AB∥CD,AB=CD=10米,OA=12米,
作OE⊥AB与E,则OE平分AB,
∴AE=AB=5米,
∴OE2=OA2﹣AE2=122﹣52=119,
∵82=64,119>64,
∴长、宽、高分别是12米,10米,8米的集装箱能放进这个仓库.
( http: / / www.21cnjy.com )
【点评】本题考查了勾股定理的应用以及垂径定理,将实际问题转化为数学问题是解题的关键.
21.已知:A,B都是x轴上的点,点A的坐标是(2,0),且线段AB的长等于4,点C的坐标是(0,3).
(1)直接写出点B的坐标;
(2)求直线BC的函数表达式.
( http: / / www.21cnjy.com )
【考点】待定系数法求一次函数解析式.
【分析】(1)根据A的坐标和AB=4,分B在A点的左边和右边两种情况求得B的坐标;
(2)根据待定系数法求得即可.
【解答】解:(1)∵A,B都是x轴上的点,点A的坐标是(2,0),且线段AB的长等于4,
∴B(6,0)或(﹣2,0);
(2)设直线BC的解析式为y=kx+b,
∵直线经过C(0,3),
∴直线BC的解析式为y=kx+3,
当B(6,0)时,0=6k+3,解得k=﹣,
当B(﹣2,0)时,0=﹣2k+3,解得k=,
∴直线BC的函数表达式为y=﹣x+3或y=x+3.
【点评】本题考查了待定系数法求一次函数的解析式,根据题意求得B的两个坐标是解题的关键.
22.在进行二次根式运算时,经常会遇到类似,的式子,其实我们还可以将其进一步变形:==;===﹣1.
以上这种将分母变为有理式的恒等变形叫做分母有理化.
再如:===﹣
===﹣2
依照上述方法解答下列问题:
(1)填空:=﹣;=﹣;=﹣.
(2)化简求值:+++…+(写出解答过程)
【考点】分母有理化.
【专题】阅读型.
【分析】(1)利用材料中所给的方法求解即可;
(2)利用分母有理化的方法求解,注意消项.
【解答】解:(1)===﹣;
===﹣;
===﹣;
故答案是:﹣;﹣;﹣;
(2)+++…+
=﹣1+﹣+﹣+…+﹣
=﹣1+
=﹣1+17
=16.
【点评】本题主要考查了分母有理化,根据 ( http: / / www.21cnjy.com )二次根式的乘除法法则进行二次根式有理化.二次根式有理化主要利用了平方差公式,所以一般二次根式的有理化因式是符合平方差公式的特点的式子.即一项符号和绝对值相同,另一项符号相反绝对值相同.
23.问题提出:求边长分别为,,(a为正整数)三角形的面积.
问题探究:为解决上述数学问题,我们采取数形结合和转化的思想方法,并采取一般问题特殊化的策略来进行探究.
探究一:当a=1时,求边长分别为、、三角形的面积.
先画一个正方形网格(每个小正方形的边长为1),再在网格中画出边长分别为,,的格点三角形△ABC(如图①).
因为AB是直角边分别为2和1的Rt△ABE的斜边,所以AB=;
因为BC是直角边分别为1和3的Rt△BCF的斜边,所以BC=;
因为AC是直角边分别为3和2的Rt△ACG的斜边,所以AC=;通过面积转化,可间接求三角形△ABC的面积.
所以,S△ABC=S正方形EFCG﹣S△ABE﹣S△BCF﹣S△ACG.
( http: / / www.21cnjy.com )
(1)直接写出图①中S△ABC=.
探究二:当a=2时,求边长分别为2,,5三角形的面积.
先画一个长方形网格(每个小长方形的长为2,宽为1),再在网格中画出边长分别为2,,5的格点三角形△ABC(如图②).
因为AB是直角边分别为2和2的Rt△ABE的斜边,所以AB=2;
因为BC是直角边分别为1和6的Rt△BCF的斜边,所以BC=;
因为AC是直角边分别为3和4的Rt△ACG的斜边,所以AC=5,通过面积转化,可间接求三角形△ABC的面积.
所以,S△ABC=S正方形EFCG﹣S△ABE﹣S△BCF﹣S△ACG
(2)直接写出图②中S△ABC=7.
探究三:当a=3时,求边长分别为,,3三角形的面积.
( http: / / www.21cnjy.com )
仿照上述方法解答下列问题:
(3)画的长方形网格中,每个小长方形的长应是2.
(4)边长分别为,,3的三角形的面积为.
问题解决:求边长分别为,,(a为正整数)三角形的面积.
(5)类比上述方法画长方形网格,每个小长方形的长应是a.
(6)边长分别为,,(a为正整数)的三角形的面积是a.
【考点】勾股定理.
【分析】(1)根据图中正方形的边长为1,再利用S△ABC=S正方形EFCG﹣S△ABE﹣S△BCF﹣S△ACG可得出结论;
(2)根据图中正方形的边长为1,再利用S△ABC=S正方形EFCG﹣S△ABE﹣S△BCF﹣S△ACG可得出结论;
(3)根据(1)(2)中正方形的边长规律可得出结论;
(4)根据题意在网格中画出图形,同(2)的方法可得出结论;
(5)根据(2)(3)中长方形的边长规律可得出结论;
(6)根据(5)中的结论画出图形即可得出三角形的面积.
【解答】解:(1)由图可知,
S△ABC=S正方形EFCG﹣S△ABE﹣S△BCF﹣S△ACG
=3×3﹣×2×1﹣×1×3﹣×2×3
=9﹣1﹣﹣3
=.
故答案为:;
(2)由图可知,
S△ABC=S正方形EFCG﹣S△ABE﹣S△BCF﹣S△ACG
=3×6﹣×2×2﹣×1×6﹣×4×3
=18﹣2﹣3﹣6
=7.
故答案为7;
(3)由(2)可知,每个小长方形的长应是2.
故答案为:2;
(4)∵=,=,3=,
∴长方形的边长为3,画图如下:
( http: / / www.21cnjy.com )
∴S△ABC=S正方形EFCG﹣S△ABE﹣S△BCF﹣S△ACG
=3×9﹣×2×3﹣﹣×1×9﹣×3×6
=27﹣3﹣9﹣
=.
故答案为:;
(5)由(1)、(2)、(4)可知,每个小长方形的长应是a.
故答案为:a;
(6)由(1)、(2)、(4)的规律可知,
边长分别为,,(a为正整数)的三角形的面积为:
S△ABC=S正方形EFCG﹣S△ABE﹣S△BCF﹣S△ACG
=3×3a﹣×2×a﹣×1×3a﹣×3×2a
=9a﹣a﹣a﹣3a
=a.
故答案为:a.
【点评】本题考查的是勾股定理,根据题意找出规律,求出长方形的边长与a的关系是解答此题的关键.
24.在创建国家卫生城市环境综合整治行 ( http: / / www.21cnjy.com )动中,某小区计划对楼体外墙进行粉刷,现有甲、乙两家装饰公司有意承接此项工程.已知甲公司的费用y(元)与粉刷面积x(x≥100)(m2)的关系如表:
粉刷面积x(m2) 100 200 300 400 …
费用y(元) 2000 4000 6000 8000 …
乙公司表示:若该小区先支付3000元的基本承包费,则可按15元/m2的价格收费.请根据以上信息,解答下列问题:
(1)若甲公司收取的费用y(元)与粉刷面积x(m2)满足我们学过某一函数关系,试确定这一函数关系式;
(2)试确定乙公司收取的费用y(元)与粉刷面积x(x≥100)(m2)满足的函数关系式;
(3)在给出的平面直角坐标系内画出(1)(2)中的函数图象,并确定若该小区粉刷面积约为800m2,则选择哪家装饰公司进行施工更合算?
( http: / / www.21cnjy.com )
【考点】一次函数的应用.
【分析】(1)根据表中的已知点的坐标确定函数的解析式即可;
(2)根据乙公司表示:若该小区先支付3000元的基本承包费,则可按15元/m2的价格收费,则y乙=3000+15x.
(3)利用两点法画出函数的图象,然后把x=800分别代入解析式即可判断.
【解答】解:(1)由表中的数据可知甲公司收取的费用y(元)与粉刷面积x(m2)成正比例,
设y=kx,把(100,2000)代入得:2000=100k,
解得k=20,
所以y甲=20x;
(2)根据题意得y乙=3000+15x.
(3)画出函数的图象如图:
( http: / / www.21cnjy.com )
把x=800代入y甲=20x得,y甲=20×800=16000(元),
把x=800代入y乙=3000+15x得,y乙=3000+15×800=15000(元),
y甲>y乙,
所以,确定若该小区粉刷面积约为800m2,则选择乙装饰公司进行施工更合算.
【点评】本题考查了一次函数的应用,主要利用了待定系数法求一次函数解析式,根据题意得出相等关系是解题的关键.
一、选择题:每小题3分,共24分.
1.下列各数:,,,﹣2,0,1.020020002…(相邻两个2之间0的个数逐次加1),其中无理数有( )
A.1个 B.2个 C.3个 D.4个
2.在平面直角坐标系中,点(﹣3,﹣1)在第( )象限.
A.第一象限 B.第二象限 C.第三象限 D.第四象限
3.下列说法不正确的是( )
A.0的平方根是0
B.一个正数的立方根是一个正数
C.8的算术平方根是4
D.﹣8的立方根是﹣2
4.下列四组线段中,可构成直角三角形的是( )
A.1.5,2,2.5 B.1,2,3 C.1,,3 D.2,3,4
5.下列计算正确的是( )
A.||=2 B.=±7 C.=﹣5 D.=﹣
6.下列函数中,y的值随x值的增大而减小的是( )
①y=8x﹣1;②y=﹣0.6x;③y=x+1;④y=(﹣)x.
A.①② B.③④ C.①③ D.②④
7.计算:(﹣2)2015 (+2)2016=( )
A.+2 B.﹣﹣2 C.﹣2 D.﹣1
8.某校甲、乙两班参加植树活动,乙班先植 ( http: / / www.21cnjy.com )树,然后甲班才开始与乙班一起植树.设甲班植树的总量为y甲(棵),乙班植树的总量为y乙(棵),两班一起植树所用的时间(从甲班开始植树时计时)为x(时),y甲、y乙分别与x之间的部分函数图象如图所示.下列说法正确的有( )
①甲班每小时植树20棵;
②乙班比甲班先植树30棵;
③甲班植树3小时两个班植树总量都是60棵;
④甲班植树超过3小时后,植树总量超过乙班.
( http: / / www.21cnjy.com )
A.1个 B.2个 C.3个 D.4个
二、填空题:每小题3分,共24分.
9.在影剧院里,若将“5排10号”记作(5,10),则(9,3)表示的座位是__________.
10.数轴上到原点距离的点表示的数是__________.
11.10﹣3的立方根是__________.
12.点M(﹣2,1)关于x轴对称的点N的坐标是__________.
13.一次函数y=3x﹣2的图象与坐标轴围成的三角形的面积是__________.
14.满足<x<的整数x是__________.
15.已知(﹣2,y1),(﹣1.5,y2 ( http: / / www.21cnjy.com )),(1,y3)是直线y=2x+b(b为常数)上的三个点,则y1,y2,y3的大小关系是__________.(用“>”表示)
16.图①所示的正方体木块棱长为6cm,沿 ( http: / / www.21cnjy.com )其相邻三个面的对角线(图中虚线)剪掉一角,得到如图②的几何体,一只蚂蚁沿着图②的几何体表面从顶点A爬行到顶点B的最短距离为__________cm.
( http: / / www.21cnjy.com )
三、作图题:6分.
17.如图所示,在方格纸上建立的平面直角坐标系中:
(1)作△ABC关于y轴的对称△A1B1C1.
(2)若线段AB上有点P,坐标为(a,b).则它在A1B1上的对称点P1的坐标为__________.
( http: / / www.21cnjy.com )
四、解答题:满分66分.
18.(16分)计算:
(1)
(2)(﹣)2
(3)(﹣2)×﹣6
(4)2﹣3+.
19.已知:如图,在△AB ( http: / / www.21cnjy.com )C中,AC=BC=5,AB=6,请以点A为原点,以AB所在的直线为x轴建立平面直角坐标系,并求出△ABC的各顶点坐标.
( http: / / www.21cnjy.com )
20.如图,某仓库入口的截面是一个半径为12米的半圆形,一个长、宽、高分别是12米,10米,8米的集装箱能放进这个仓库吗?请通过计算说明.
21.已知:A,B都是x轴上的点,点A的坐标是(2,0),且线段AB的长等于4,点C的坐标是(0,3).
(1)直接写出点B的坐标;
(2)求直线BC的函数表达式.
( http: / / www.21cnjy.com )
22.在进行二次根式运算时,经常会遇到类似,的式子,其实我们还可以将其进一步变形:==;===﹣1.
以上这种将分母变为有理式的恒等变形叫做分母有理化.
再如:===﹣
===﹣2
依照上述方法解答下列问题:
(1)填空:=__________;=__________;=__________.
(2)化简求值:+++…+(写出解答过程)
23.问题提出:求边长分别为,,(a为正整数)三角形的面积.
问题探究:为解决上述数学问题,我们采取数形结合和转化的思想方法,并采取一般问题特殊化的策略来进行探究.
探究一:当a=1时,求边长分别为、、三角形的面积.
先画一个正方形网格(每个小正方形的边长为1),再在网格中画出边长分别为,,的格点三角形△ABC(如图①).
因为AB是直角边分别为2和1的Rt△ABE的斜边,所以AB=;
因为BC是直角边分别为1和3的Rt△BCF的斜边,所以BC=;
因为AC是直角边分别为3和2的Rt△ACG的斜边,所以AC=;通过面积转化,可间接求三角形△ABC的面积.
所以,S△ABC=S正方形EFCG﹣S△ABE﹣S△BCF﹣S△ACG.
( http: / / www.21cnjy.com )
(1)直接写出图①中S△ABC=__________.
探究二:当a=2时,求边长分别为2,,5三角形的面积.
先画一个长方形网格(每个小长方形的长为2,宽为1),再在网格中画出边长分别为2,,5的格点三角形△ABC(如图②).
因为AB是直角边分别为2和2的Rt△ABE的斜边,所以AB=2;
因为BC是直角边分别为1和6的Rt△BCF的斜边,所以BC=;
因为AC是直角边分别为3和4的Rt△ACG的斜边,所以AC=5,通过面积转化,可间接求三角形△ABC的面积.
所以,S△ABC=S正方形EFCG﹣S△ABE﹣S△BCF﹣S△ACG
(2)直接写出图②中S△ABC=__________.
探究三:当a=3时,求边长分别为,,3三角形的面积.
( http: / / www.21cnjy.com )
仿照上述方法解答下列问题:
(3)画的长方形网格中,每个小长方形的长应是__________.
(4)边长分别为,,3的三角形的面积为__________.
问题解决:求边长分别为,,(a为正整数)三角形的面积.
(5)类比上述方法画长方形网格,每个小长方形的长应是__________.
(6)边长分别为,,(a为正整数)的三角形的面积是__________.
24.在创建国家卫生城市环境综合整治行 ( http: / / www.21cnjy.com )动中,某小区计划对楼体外墙进行粉刷,现有甲、乙两家装饰公司有意承接此项工程.已知甲公司的费用y(元)与粉刷面积x(x≥100)(m2)的关系如表:
粉刷面积x(m2) 100 200 300 400 …
费用y(元) 2000 4000 6000 8000 …
乙公司表示:若该小区先支付3000元的基本承包费,则可按15元/m2的价格收费.请根据以上信息,解答下列问题:
(1)若甲公司收取的费用y(元)与粉刷面积x(m2)满足我们学过某一函数关系,试确定这一函数关系式;
(2)试确定乙公司收取的费用y(元)与粉刷面积x(x≥100)(m2)满足的函数关系式;
(3)在给出的平面直角坐标系内画出(1)(2)中的函数图象,并确定若该小区粉刷面积约为800m2,则选择哪家装饰公司进行施工更合算?
( http: / / www.21cnjy.com )
2015-2016学年山东省青岛市黄岛区八年级(上)期中数学试卷
一、选择题:每小题3分,共24分.
1.下列各数:,,,﹣2,0,1.020020002…(相邻两个2之间0的个数逐次加1),其中无理数有( )
A.1个 B.2个 C.3个 D.4个
【考点】无理数.
【分析】根据无理数的三种形式求解.
【解答】解:=2,=2,
无理数有:,1.020020002…,共2个.
故选B.
【点评】本题考查了无理数的知识,解答本题的关键是掌握无理数的三种形式:①开方开不尽的数,②无限不循环小数,③含有π的数.
2.在平面直角坐标系中,点(﹣3,﹣1)在第( )象限.
A.第一象限 B.第二象限 C.第三象限 D.第四象限
【考点】点的坐标.
【专题】数形结合.
【分析】根据所给点的横纵坐标的符号可得所在象限.
【解答】解:∵所给点的横坐标是﹣3为负数,纵坐标是﹣1为负数,
∴点(﹣3,﹣1)在第三象限,
故选C.
【点评】考查象限内点的符号特点;用到的知识点为:符号为(﹣,﹣)的点在第三象限.
3.下列说法不正确的是( )
A.0的平方根是0
B.一个正数的立方根是一个正数
C.8的算术平方根是4
D.﹣8的立方根是﹣2
【考点】立方根;平方根;算术平方根.
【专题】计算题.
【分析】原式各选项利用平方根,算术平方根,以及立方根定义判断即可.
【解答】解:A、0的平方根是0,正确;
B、一个正数的立方根是一个正数,正确;
C、8的算术平方根是2,错误;
D、﹣8的立方根是﹣2,正确,
故选C
【点评】此题考查了立方根,平方根,以及算术平方根,熟练掌握各自的定义是解本题的关键.
4.下列四组线段中,可构成直角三角形的是( )
A.1.5,2,2.5 B.1,2,3 C.1,,3 D.2,3,4
【考点】勾股定理的逆定理.
【分析】根据勾股定理的逆定理对各选项进行逐一分析即可.
【解答】解:A、∵1.52+22=6.25=2.52,∴能够成直角三角形,故本选项正确;
B、∵1+2=3,∴不能构成三角形,故本选项错误;
C、∵1+<3,不能构成三角形,故本选项错误;
D、∵22+32=13≠42,∴不能够成直角三角形,故本选项错误.
故选A.
【点评】本题考查的是勾股定理的逆定理,熟知如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形就是直角三角形是解答此题的关键.
5.下列计算正确的是( )
A.||=2 B.=±7 C.=﹣5 D.=﹣
【考点】立方根;算术平方根.
【分析】根据算术平方根、立方根的定义,即可解答.
【解答】解:A、||=﹣,故错误;
B、=7,故错误;
C、=5,故错误;
D、,正确.
故选:D.
【点评】本题考查了算术平方根、立方根,解决本题的关键是熟记算术平方根、立方根的定义.
6.下列函数中,y的值随x值的增大而减小的是( )
①y=8x﹣1;②y=﹣0.6x;③y=x+1;④y=(﹣)x.
A.①② B.③④ C.①③ D.②④
【考点】一次函数的性质;正比例函数的性质.
【分析】根据一次函数的性质对各小题进行逐一分析即可.
【解答】解:①∵y=8x﹣1中,k=8>0,∴y的值随x值的增大而增大,故本小题错误;
②∵y=﹣0.6x中,k=﹣0.6<0,∴y的值随x值的增大而减小,故本小题正确;
③∵y=x+1中,k=>0,∴y的值随x值的增大而增大,故本小题错误;
④∵y=(﹣)x中,k=﹣<0,∴y的值随x值的增大而减小,故本小题正确.
故选D.
【点评】本题考查的是一次函数的性质,熟知一次函数的增减性与系数k的关系是解答此题的关键.
7.计算:(﹣2)2015 (+2)2016=( )
A.+2 B.﹣﹣2 C.﹣2 D.﹣1
【考点】二次根式的混合运算.
【分析】逆用积的乘方公式即可求解.
【解答】解:原式=【(﹣2)(+2)】2015(+2)=(﹣1)2015(+2)=﹣(+2)=﹣﹣2.
故选B.
【点评】本题考查了二次根式的运算,逆用积的乘方公式把已知的式子变形成【(﹣2)(+2)】2015(+2)的形式是关键.
8.某校甲、乙两班参加植树活动,乙 ( http: / / www.21cnjy.com )班先植树,然后甲班才开始与乙班一起植树.设甲班植树的总量为y甲(棵),乙班植树的总量为y乙(棵),两班一起植树所用的时间(从甲班开始植树时计时)为x(时),y甲、y乙分别与x之间的部分函数图象如图所示.下列说法正确的有( )
①甲班每小时植树20棵;
②乙班比甲班先植树30棵;
③甲班植树3小时两个班植树总量都是60棵;
④甲班植树超过3小时后,植树总量超过乙班.
( http: / / www.21cnjy.com )
A.1个 B.2个 C.3个 D.4个
【考点】一次函数的应用.
【分析】由图可知:甲班6小时植树1 ( http: / / www.21cnjy.com )20棵,所以甲班每小时植树120÷6=20(棵);甲班开始植树时乙班已经先植树30棵;甲班植树3小时两个班植树总量相等,根据甲班植树的速度可知此时植树的数量;当x>3时,y甲>y乙,即可判断甲班植树超过3小时后,植树总量超过乙班.
【解答】解:由图可知:甲班6小时植树120棵,所以甲班每小时植树120÷6=20(棵),故①正确;
由图象可知:甲班开始植树时乙班已经先植树30棵;故②正确;
由图象可知:甲班植树3小时两个班植树总量相等,根据甲班植树的速度可知此时植树的数为20×3=609棵),故③正确;
由图象可知,当x>3时,y甲在y乙的上方,则甲班植树超过3小时后,植树总量超过乙班,故④正确.
故选:D.
【点评】此题主要考查了一次函数的应用,读懂图,获取正确信息是解题关键.
二、填空题:每小题3分,共24分.
9.在影剧院里,若将“5排10号”记作(5,10),则(9,3)表示的座位是9排3号.
【考点】坐标确定位置.
【分析】根据有序数对(排,号),可得答案.
【解答】解:在影剧院里,若将“5排10号”记作(5,10),则(9,3)表示的座位是9排3号.
故答案为:9排3号.
【点评】本题考查了坐标确定位置,利用(排,号)有序数对表示位置是解题关键.
10.数轴上到原点距离的点表示的数是±.
【考点】实数与数轴.
【分析】根据绝对值的几何意义:一个数的绝对值就是在数轴上表示这个数的点到原点的距离,可知本题就是求绝对值为的数.
【解答】解:根据绝对值的几何意义,得数轴上到原点的距离为的点表示的数,即绝对值为的数,为±.
故答案为±.
【点评】本题考查实数与数轴,绝对值的几何意义.要知道,实数与数轴上的点是一一对应的,互为相反数的两个数到原点的距离相等.
11.10﹣3的立方根是0.1.
【考点】立方根.
【分析】先化简10﹣3=0.001,根据立方根的定义即可解答.
【解答】解:10﹣3=0.001,0.001的立方根为0.1,
故答案为:0.1.
【点评】本题考查了立方根,解决本题的关键是熟记立方根的定义.
12.点M(﹣2,1)关于x轴对称的点N的坐标是N(﹣2,﹣1).
【考点】关于x轴、y轴对称的点的坐标.
【专题】计算题.
【分析】本题比较容易,考查平面直角坐标系中任 ( http: / / www.21cnjy.com )意一点P(x,y),关于x轴对称的点的坐标是(x,﹣y),即横坐标相等,纵坐标互为相反数;据此可得答案.
【解答】解:根据题意,M与N关于x轴对称,
则其横坐标相等,纵坐标互为相反数;
所以N点坐标是(﹣2,﹣1).
故答案为:(﹣2,﹣1).
【点评】本题考查关于x轴对称的两点的坐标之间的关系,关键是掌握两点关于x轴对称则横坐标相等,纵坐标互为相反数.
13.一次函数y=3x﹣2的图象与坐标轴围成的三角形的面积是.
【考点】一次函数图象上点的坐标特征.
【分析】先根据坐标轴上点的坐标特征求出直线与坐标轴的交点坐标,然后根据三角形面积公式求解.
【解答】解:当x=0时,y=3x﹣2=﹣2,则直线与y轴的交点坐标为(0,﹣2);
当y=0时,3x﹣2=0,解得x=,则直线与x轴的交点坐标为(,0),
所以函数y=3x﹣2的图象与坐标轴围成的三角形面积=×2×=.
故答案为.
【点评】本题考查了一次函数图象上点的坐标特征:直线上任意一点的坐标都满足函数关系式y=kx+b.
14.满足<x<的整数x是﹣1,0,1,2.
【考点】估算无理数的大小.
【分析】求出﹣,的范围,即可得出答案.
【解答】解:∵﹣2<﹣<﹣1,2<<3,
∴满足<x<的整数x有﹣1,0,1,2,
故答案为:﹣1,0,1,2.
【点评】本题考查了估算无理数的大小的应用,关键是确定﹣,的范围.
15.已知(﹣2,y1), ( http: / / www.21cnjy.com )(﹣1.5,y2),(1,y3)是直线y=2x+b(b为常数)上的三个点,则y1,y2,y3的大小关系是y3>y2>y1.(用“>”表示)
【考点】一次函数图象上点的坐标特征.
【分析】由y=2x+b(b为常数)可知k=2>0,故y随x的增大而增大,由﹣2<﹣1.5<1,可得y1,y2,y3的大小关系.
【解答】解:∵k=2>0,
∴y随x的增大而增大,
∵﹣2<﹣1.5<1,
∵y3>y2>y1,
故答案为:y3>y2>y1.
【点评】本题主要考查一次函数的增减性,熟练掌握一次函数的增减性是解题的关键.
16.图①所示的正方体木块棱长为6cm,沿其相邻三个面的对角线(图中虚线)剪掉一角,得到如图②的几何体,一只蚂蚁沿着图②的几何体表面从顶点A爬行到顶点B的最短距离为(3+3)cm.
( http: / / www.21cnjy.com )
【考点】平面展开-最短路径问题;截一个几何体.
【专题】压轴题;数形结合.
【分析】要求蚂蚁爬行的最短距离,需将图②的几何体表面展开,进而根据“两点之间线段最短”得出结果.
【解答】解:如图所示:
( http: / / www.21cnjy.com )
△BCD是等腰直角三角形,△ACD是等边三角形,
在Rt△BCD中,CD==6cm,
∴BE=CD=3cm,
在Rt△ACE中,AE==3cm,
∴从顶点A爬行到顶点B的最短距离为(3+3)cm.
故答案为:(3+3).
【点评】考查了平面展开﹣最短路径问题,本题就是把图②的几何体表面展开成平面图形,根据等腰直角三角形的性质和等边三角形的性质解决问题.
三、作图题:6分.
17.如图所示,在方格纸上建立的平面直角坐标系中:
(1)作△ABC关于y轴的对称△A1B1C1.
(2)若线段AB上有点P,坐标为(a,b).则它在A1B1上的对称点P1的坐标为(﹣a,b).
( http: / / www.21cnjy.com )
【考点】作图-轴对称变换.
【分析】(1)作出各点关于y轴的对称点,再顺次连接各点即可;
(2)根据关于y轴对称的点的坐标特点即可得出结论.
【解答】解:(1)如图所示;
(2)∵P(a,b),
∴P1(﹣a,b).
故答案为:(﹣a,b).
( http: / / www.21cnjy.com )
【点评】本题考查的是作图﹣轴对称变换,熟知关于y轴对称的点的坐标特点是解答此题的关键.
四、解答题:满分66分.
18.(16分)计算:
(1)
(2)(﹣)2
(3)(﹣2)×﹣6
(4)2﹣3+.
【考点】二次根式的混合运算.
【分析】(1)首先化简二次根式,然后进行乘除运算即可;
(2)利用完全平方公式计算即可;
(3)首先利用分配律计算乘法,化简二次根式,然后合并同类二次根式即可;
(4)首先化简二次根式,然后合并同类二次根式即可.
【解答】解:(1)原式==10;
(2)原式=5+2﹣2=7﹣2;
(3)原式=﹣2﹣3=3﹣6﹣3=﹣6;
(4)原式=4﹣+=4.
【点评】本题考查的是二次根式的混合运算,在进行此类运算时,一般先把二次根式化为最简二次根式的形式后再运算.
19.已知:如图,在△A ( http: / / www.21cnjy.com )BC中,AC=BC=5,AB=6,请以点A为原点,以AB所在的直线为x轴建立平面直角坐标系,并求出△ABC的各顶点坐标.
( http: / / www.21cnjy.com )
【考点】坐标与图形性质.
【分析】以点A为原点,以AB所在的直线为x轴建立平面直角坐标系,然后过点C作AD⊥AB于D,根据等腰三角形三线合一的性质可得BD=AD=AB,再利用勾股定理列式求出CD,然后写出各点的坐标即可
【解答】解:坐标系如图,
( http: / / www.21cnjy.com )
过点C作CD⊥AB于D,
∵AB=AC=13,BC=10,
∴BD=AD=AB=×6=3,
由勾股定理得,CD===4.
∴A(0,0),B(﹣6,0),C(﹣3,4).
【点评】此题考查坐标与图形的性质,等腰三角形三线合一的性质,勾股定理的应用,作底边上的高,构造出直角三角形并利用性质是解题的关键.
20.如图,某仓库入口的截面是一个半径为12米的半圆形,一个长、宽、高分别是12米,10米,8米的集装箱能放进这个仓库吗?请通过计算说明.
【考点】勾股定理的应用.
【分析】设ABCD是矩形,作OE⊥AB与E,首先根据垂径定理求得AE=5米,然后根据勾股定理求得OE的长,再与箱子的高比较即可判定.
【解答】解:如图,设ABCD是矩形,则AB∥CD,AB=CD=10米,OA=12米,
作OE⊥AB与E,则OE平分AB,
∴AE=AB=5米,
∴OE2=OA2﹣AE2=122﹣52=119,
∵82=64,119>64,
∴长、宽、高分别是12米,10米,8米的集装箱能放进这个仓库.
( http: / / www.21cnjy.com )
【点评】本题考查了勾股定理的应用以及垂径定理,将实际问题转化为数学问题是解题的关键.
21.已知:A,B都是x轴上的点,点A的坐标是(2,0),且线段AB的长等于4,点C的坐标是(0,3).
(1)直接写出点B的坐标;
(2)求直线BC的函数表达式.
( http: / / www.21cnjy.com )
【考点】待定系数法求一次函数解析式.
【分析】(1)根据A的坐标和AB=4,分B在A点的左边和右边两种情况求得B的坐标;
(2)根据待定系数法求得即可.
【解答】解:(1)∵A,B都是x轴上的点,点A的坐标是(2,0),且线段AB的长等于4,
∴B(6,0)或(﹣2,0);
(2)设直线BC的解析式为y=kx+b,
∵直线经过C(0,3),
∴直线BC的解析式为y=kx+3,
当B(6,0)时,0=6k+3,解得k=﹣,
当B(﹣2,0)时,0=﹣2k+3,解得k=,
∴直线BC的函数表达式为y=﹣x+3或y=x+3.
【点评】本题考查了待定系数法求一次函数的解析式,根据题意求得B的两个坐标是解题的关键.
22.在进行二次根式运算时,经常会遇到类似,的式子,其实我们还可以将其进一步变形:==;===﹣1.
以上这种将分母变为有理式的恒等变形叫做分母有理化.
再如:===﹣
===﹣2
依照上述方法解答下列问题:
(1)填空:=﹣;=﹣;=﹣.
(2)化简求值:+++…+(写出解答过程)
【考点】分母有理化.
【专题】阅读型.
【分析】(1)利用材料中所给的方法求解即可;
(2)利用分母有理化的方法求解,注意消项.
【解答】解:(1)===﹣;
===﹣;
===﹣;
故答案是:﹣;﹣;﹣;
(2)+++…+
=﹣1+﹣+﹣+…+﹣
=﹣1+
=﹣1+17
=16.
【点评】本题主要考查了分母有理化,根据 ( http: / / www.21cnjy.com )二次根式的乘除法法则进行二次根式有理化.二次根式有理化主要利用了平方差公式,所以一般二次根式的有理化因式是符合平方差公式的特点的式子.即一项符号和绝对值相同,另一项符号相反绝对值相同.
23.问题提出:求边长分别为,,(a为正整数)三角形的面积.
问题探究:为解决上述数学问题,我们采取数形结合和转化的思想方法,并采取一般问题特殊化的策略来进行探究.
探究一:当a=1时,求边长分别为、、三角形的面积.
先画一个正方形网格(每个小正方形的边长为1),再在网格中画出边长分别为,,的格点三角形△ABC(如图①).
因为AB是直角边分别为2和1的Rt△ABE的斜边,所以AB=;
因为BC是直角边分别为1和3的Rt△BCF的斜边,所以BC=;
因为AC是直角边分别为3和2的Rt△ACG的斜边,所以AC=;通过面积转化,可间接求三角形△ABC的面积.
所以,S△ABC=S正方形EFCG﹣S△ABE﹣S△BCF﹣S△ACG.
( http: / / www.21cnjy.com )
(1)直接写出图①中S△ABC=.
探究二:当a=2时,求边长分别为2,,5三角形的面积.
先画一个长方形网格(每个小长方形的长为2,宽为1),再在网格中画出边长分别为2,,5的格点三角形△ABC(如图②).
因为AB是直角边分别为2和2的Rt△ABE的斜边,所以AB=2;
因为BC是直角边分别为1和6的Rt△BCF的斜边,所以BC=;
因为AC是直角边分别为3和4的Rt△ACG的斜边,所以AC=5,通过面积转化,可间接求三角形△ABC的面积.
所以,S△ABC=S正方形EFCG﹣S△ABE﹣S△BCF﹣S△ACG
(2)直接写出图②中S△ABC=7.
探究三:当a=3时,求边长分别为,,3三角形的面积.
( http: / / www.21cnjy.com )
仿照上述方法解答下列问题:
(3)画的长方形网格中,每个小长方形的长应是2.
(4)边长分别为,,3的三角形的面积为.
问题解决:求边长分别为,,(a为正整数)三角形的面积.
(5)类比上述方法画长方形网格,每个小长方形的长应是a.
(6)边长分别为,,(a为正整数)的三角形的面积是a.
【考点】勾股定理.
【分析】(1)根据图中正方形的边长为1,再利用S△ABC=S正方形EFCG﹣S△ABE﹣S△BCF﹣S△ACG可得出结论;
(2)根据图中正方形的边长为1,再利用S△ABC=S正方形EFCG﹣S△ABE﹣S△BCF﹣S△ACG可得出结论;
(3)根据(1)(2)中正方形的边长规律可得出结论;
(4)根据题意在网格中画出图形,同(2)的方法可得出结论;
(5)根据(2)(3)中长方形的边长规律可得出结论;
(6)根据(5)中的结论画出图形即可得出三角形的面积.
【解答】解:(1)由图可知,
S△ABC=S正方形EFCG﹣S△ABE﹣S△BCF﹣S△ACG
=3×3﹣×2×1﹣×1×3﹣×2×3
=9﹣1﹣﹣3
=.
故答案为:;
(2)由图可知,
S△ABC=S正方形EFCG﹣S△ABE﹣S△BCF﹣S△ACG
=3×6﹣×2×2﹣×1×6﹣×4×3
=18﹣2﹣3﹣6
=7.
故答案为7;
(3)由(2)可知,每个小长方形的长应是2.
故答案为:2;
(4)∵=,=,3=,
∴长方形的边长为3,画图如下:
( http: / / www.21cnjy.com )
∴S△ABC=S正方形EFCG﹣S△ABE﹣S△BCF﹣S△ACG
=3×9﹣×2×3﹣﹣×1×9﹣×3×6
=27﹣3﹣9﹣
=.
故答案为:;
(5)由(1)、(2)、(4)可知,每个小长方形的长应是a.
故答案为:a;
(6)由(1)、(2)、(4)的规律可知,
边长分别为,,(a为正整数)的三角形的面积为:
S△ABC=S正方形EFCG﹣S△ABE﹣S△BCF﹣S△ACG
=3×3a﹣×2×a﹣×1×3a﹣×3×2a
=9a﹣a﹣a﹣3a
=a.
故答案为:a.
【点评】本题考查的是勾股定理,根据题意找出规律,求出长方形的边长与a的关系是解答此题的关键.
24.在创建国家卫生城市环境综合整治行 ( http: / / www.21cnjy.com )动中,某小区计划对楼体外墙进行粉刷,现有甲、乙两家装饰公司有意承接此项工程.已知甲公司的费用y(元)与粉刷面积x(x≥100)(m2)的关系如表:
粉刷面积x(m2) 100 200 300 400 …
费用y(元) 2000 4000 6000 8000 …
乙公司表示:若该小区先支付3000元的基本承包费,则可按15元/m2的价格收费.请根据以上信息,解答下列问题:
(1)若甲公司收取的费用y(元)与粉刷面积x(m2)满足我们学过某一函数关系,试确定这一函数关系式;
(2)试确定乙公司收取的费用y(元)与粉刷面积x(x≥100)(m2)满足的函数关系式;
(3)在给出的平面直角坐标系内画出(1)(2)中的函数图象,并确定若该小区粉刷面积约为800m2,则选择哪家装饰公司进行施工更合算?
( http: / / www.21cnjy.com )
【考点】一次函数的应用.
【分析】(1)根据表中的已知点的坐标确定函数的解析式即可;
(2)根据乙公司表示:若该小区先支付3000元的基本承包费,则可按15元/m2的价格收费,则y乙=3000+15x.
(3)利用两点法画出函数的图象,然后把x=800分别代入解析式即可判断.
【解答】解:(1)由表中的数据可知甲公司收取的费用y(元)与粉刷面积x(m2)成正比例,
设y=kx,把(100,2000)代入得:2000=100k,
解得k=20,
所以y甲=20x;
(2)根据题意得y乙=3000+15x.
(3)画出函数的图象如图:
( http: / / www.21cnjy.com )
把x=800代入y甲=20x得,y甲=20×800=16000(元),
把x=800代入y乙=3000+15x得,y乙=3000+15×800=15000(元),
y甲>y乙,
所以,确定若该小区粉刷面积约为800m2,则选择乙装饰公司进行施工更合算.
【点评】本题考查了一次函数的应用,主要利用了待定系数法求一次函数解析式,根据题意得出相等关系是解题的关键.
同课章节目录
