六年级上册数学人教版《数学广角——数与形》课件(共17张PPT)
文档属性
| 名称 | 六年级上册数学人教版《数学广角——数与形》课件(共17张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 12.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-28 11:36:32 | ||
图片预览


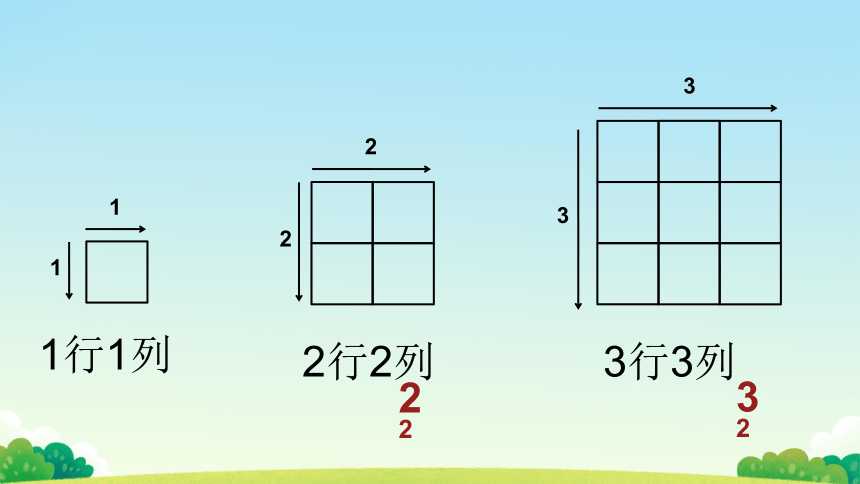


文档简介
(共17张PPT)
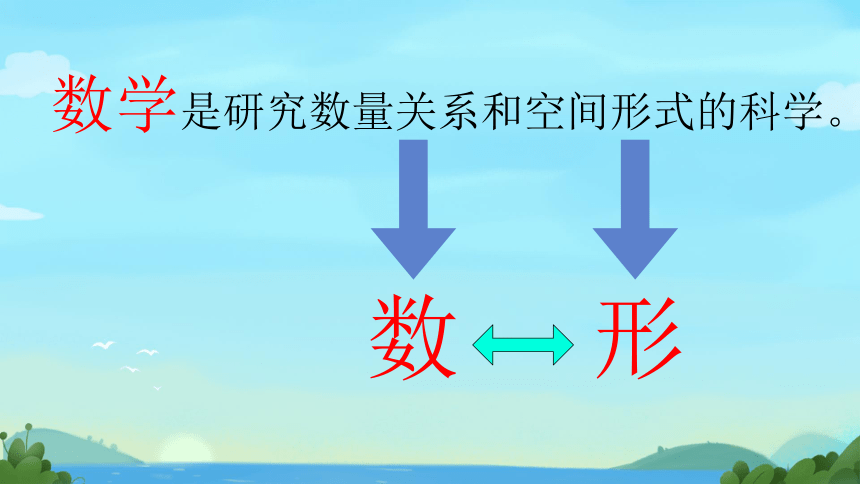
数学
嗨!
数学是研究数量关系和空间形式的科学。
数
形
数与形
人教版小学数学六年级上册
1
1
2
2
3
3
22
32
1行1列
2行2列
3行3列
… …
… …
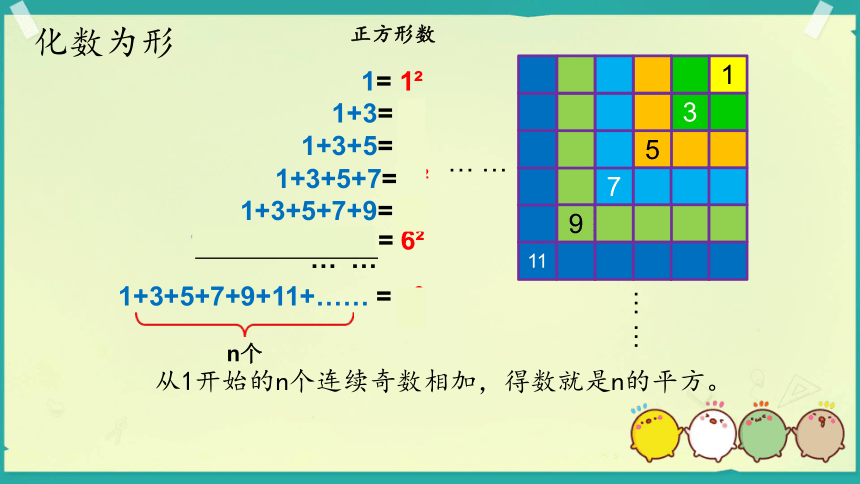
1= 1
1+3= 2
1+3+5= 3
1+3+5+7= 4
1+3+5+7+9= 5
1+3+5+7+9+11 = 6
… …
1+3+5+7+9+11+…… = n
n个
正方形数
1
3
5
7
9
11
化数为形
从1开始的n个连续奇数相加,得数就是n的平方。
规律:从1开始,n个连续的奇数相加, 得数就是n的平方。
1+3+5+……+(2n-1) = n2
n个连续奇数
1+3+5+7+9+11+13+15+17=( )
B 7
A 9
失败!!!
C
选一选我会选
1+3+5+1+3+5+7+9=( )
B.3 +5
A.8
D.以上全对
C.62
① 1+3+5+7+5+3+1=( )
25
根据规律算一算。
② 1+3+5+7+9+11+13+11+9+7+5+3+1=( )
7 =49
6 =36
85
4 =16
3 =9
拓展延伸
你能算出下面式子的结果吗?
2 + 4 + 6 + ... + 2n=
2 + 4 + 6 + ... + 2n
=(1+1)+(3+1)+(5+1)+ … +(2n-1+1)
=(1+3+5+…+2n-1)+(1+1+…+1)
= n +n
方法1:
= n(n+1)
方法2:
2 + 4 + 6 + ... + 2n
=(2+2n)×n÷2
= 2(1+n)×n÷2
=(1+n)×n
=(n+1)×n
2+4=
2×3
3×4
4×5
n×(n+1)
从2开始n个连续偶数的和等于
2+4+6+8=
2+4+6=
2
4
6
8
2 + 4 + 6 + ... + 2n=n(n+1)
2=1×2
方法3:
当遇到复杂的数学问题时,我们可以利用数形结合的思想和方法将问题变直观、简单,从而快速地解决问题!
数缺形时少直观,
形少数时难入微,
数形结合百般好,
割裂分家万事休。
数学
嗨!
数学是研究数量关系和空间形式的科学。
数
形
数与形
人教版小学数学六年级上册
1
1
2
2
3
3
22
32
1行1列
2行2列
3行3列
… …
… …
1= 1
1+3= 2
1+3+5= 3
1+3+5+7= 4
1+3+5+7+9= 5
1+3+5+7+9+11 = 6
… …
1+3+5+7+9+11+…… = n
n个
正方形数
1
3
5
7
9
11
化数为形
从1开始的n个连续奇数相加,得数就是n的平方。
规律:从1开始,n个连续的奇数相加, 得数就是n的平方。
1+3+5+……+(2n-1) = n2
n个连续奇数
1+3+5+7+9+11+13+15+17=( )
B 7
A 9
失败!!!
C
选一选我会选
1+3+5+1+3+5+7+9=( )
B.3 +5
A.8
D.以上全对
C.62
① 1+3+5+7+5+3+1=( )
25
根据规律算一算。
② 1+3+5+7+9+11+13+11+9+7+5+3+1=( )
7 =49
6 =36
85
4 =16
3 =9
拓展延伸
你能算出下面式子的结果吗?
2 + 4 + 6 + ... + 2n=
2 + 4 + 6 + ... + 2n
=(1+1)+(3+1)+(5+1)+ … +(2n-1+1)
=(1+3+5+…+2n-1)+(1+1+…+1)
= n +n
方法1:
= n(n+1)
方法2:
2 + 4 + 6 + ... + 2n
=(2+2n)×n÷2
= 2(1+n)×n÷2
=(1+n)×n
=(n+1)×n
2+4=
2×3
3×4
4×5
n×(n+1)
从2开始n个连续偶数的和等于
2+4+6+8=
2+4+6=
2
4
6
8
2 + 4 + 6 + ... + 2n=n(n+1)
2=1×2
方法3:
当遇到复杂的数学问题时,我们可以利用数形结合的思想和方法将问题变直观、简单,从而快速地解决问题!
数缺形时少直观,
形少数时难入微,
数形结合百般好,
割裂分家万事休。
