初中数学苏科版八年级上册1.3 探索三角形全等的条件复习课件(58张PPT)
文档属性
| 名称 | 初中数学苏科版八年级上册1.3 探索三角形全等的条件复习课件(58张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-28 14:34:32 | ||
图片预览








文档简介
(共58张PPT)
第1章 全等三角形
1.3 探索三角形全等的条件
1
学习目标
2
课时导入
3
感悟新知
4
随堂检测
5
课堂小结
全等三角形的判定方法——边角边(SAS)
全等三角形的判定方法——角边角(ASA)
全等三角形的判定方法——角角边(AAS)
全等三角形的判定方法——边边边(SSS)
三角形的稳定性
用尺规作角平分线和垂线
直角三角形全等的判定方法——斜边、直角边(HL)
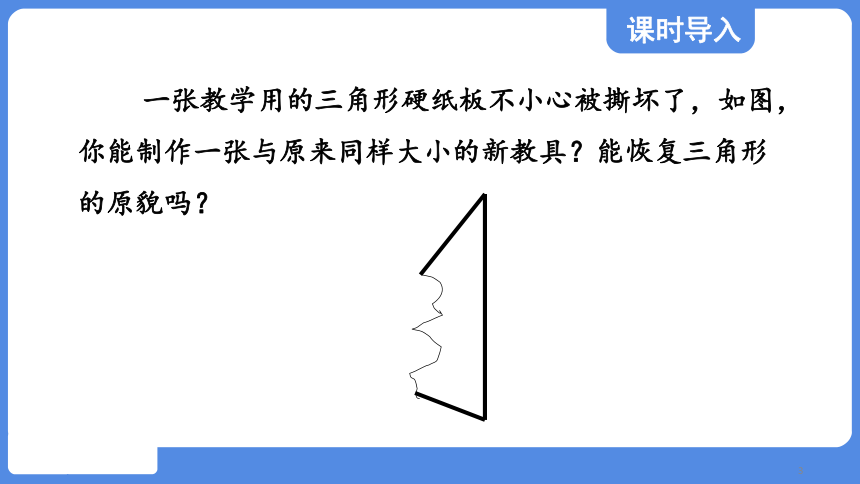
一张教学用的三角形硬纸板不小心被撕坏了,如图,你能制作一张与原来同样大小的新教具?能恢复三角形的原貌吗?
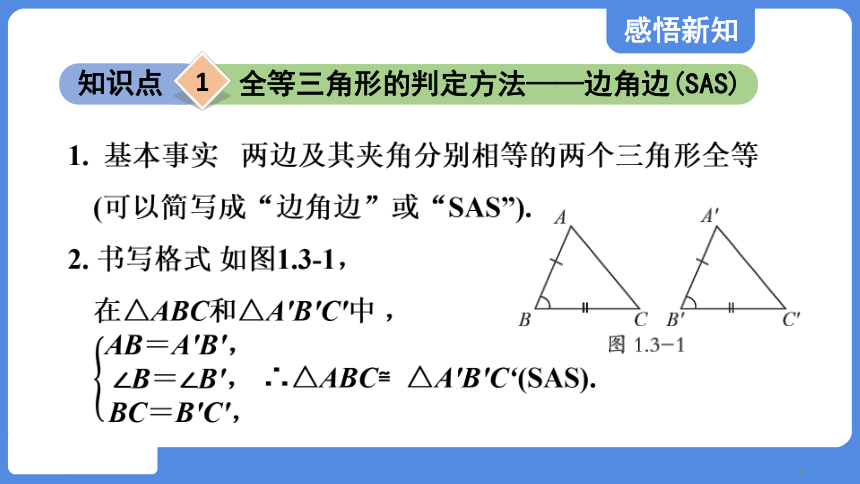
1. 基本事实 两边及其夹角分别相等的两个三角形全等(可以简写成“边角边”或“SAS”).
2. 书写格式 如图1.3-1,
在△ABC和△A'B'C'中 ,
∴△ABC≌△A'B'C‘(SAS).
知识点
全等三角形的判定方法——边角边(SAS)
1
要点提醒
1. 相等的元素:两边及其夹角.
2. 书写顺序:边→角→边.
3. 两边和其中一边的对角分别相等的两个三角形不一定全等.
例 1
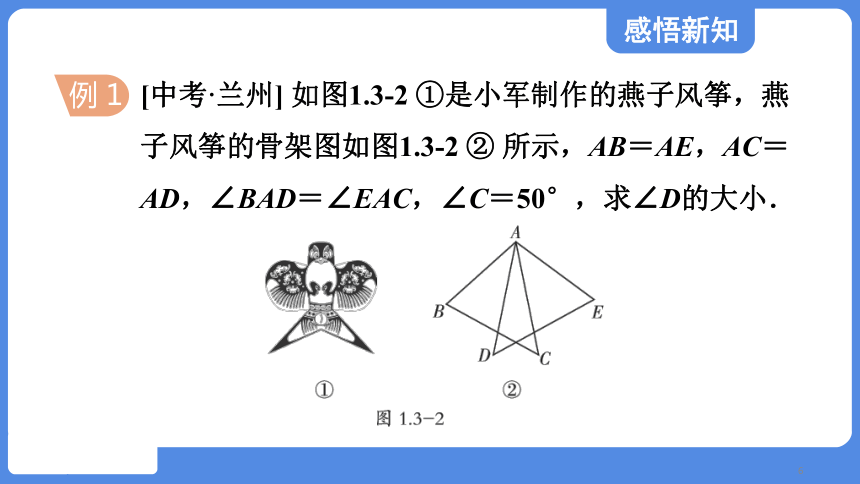
[中考·兰州] 如图1.3-2 ①是小军制作的燕子风筝,燕子风筝的骨架图如图1.3-2 ② 所示,AB=AE,AC=AD,∠BAD=∠EAC,∠C=50°,求∠D的大小.
解题秘方:紧扣隐含公共角证明∠ BAC=∠EAD,利用“SAS”证明△BAC ≌△EAD,最后由全等三角形的性质求解.
解:∵∠BAD=∠EAC,
∴∠BAD+∠CAD=∠EAC+∠CAD,
即∠BAC=∠EAD.
在△BAC和△EAD中,
∴△BAC≌△EAD(SAS).∴∠D=∠C=50°.
方法点拨
常见的隐含等角的情况:①公共角相等;②对顶角相等;③等角加(或减)等角,其和(或差)仍相等;④同角或等角的余(或补) 角相等;⑤由角平分线的定义得出角相等;⑥由垂直的定义得出角相等;⑦由平行线得到同位角或内错角相等.
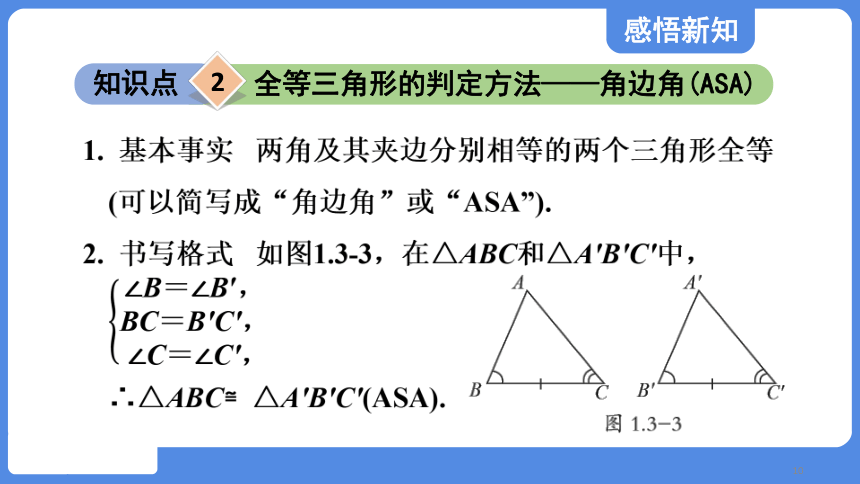
1. 基本事实 两角及其夹边分别相等的两个三角形全等(可以简写成“角边角”或“ASA”).
2. 书写格式 如图1.3-3,在△ABC和△A′B′C′中,
∴△ABC≌△A′B′C′(ASA).
知识点
全等三角形的判定方法——角边角(ASA)
2
要点提醒
1. 相等的元素:两角及其夹边.
2. 书写顺序:角→边→角.
3. 夹边即两个角的公共边.
[期末·杭州] 如图1.3-4,点A、D、C、E在同一条直线上,AB∥EF,AB=EF, ∠B=∠F,AE=10,AC=7,则CD的长为( )
A. 5.5
B. 4
C. 4.5
D. 3
例 2
解题秘方:解题的关键是由平行线得出角相等,构造两角及其夹边对应相等,利用全等三角形的判定与性质求出线段之间的数量关系.
答案:B
解:∵ AB∥EF(已知),
∴∠A=∠E(两直线平行,内错角相等).
在△ABC和△EFD中,
∴△ABC≌△EFD(ASA).
∴ ED=AC=7(全等三角形的对应边相等).
∴ AD=AE-ED=10-7=3.∴ CD=AC-AD=7-3=4.
方法点拨
运用“ASA”判定两个三角形全等,既要找边相等,又要找角相等,除已知条件外,看缺什么条件,就去找什么条件. 另外,判定两个三角形全等后可以运用其性质,得出线段或角的相等关系.
1. 基本事实(ASA)的推论 两角分别相等且其中一组等角的对边相等的两个三角形全等(可以简写成“角角边”或“AAS”).
知识点
全等三角形的判定方法——角角边(AAS)
3
2. 书写格式 如图1.3-5,在△ABC和△A'B'C'中,
∴△ABC≌△A'B'C'(AAS).
3. 特别解读
(1)判定两个三角形全等的三个条件中,“边”是必不可少的;
(2)由于“角角边”和“角边角”是可以互相转化的,故能用“角角边”证明的问题,一般也可以用“角边角”证明;
(3)在运用“ASA”和“AAS”判定时,要注意“夹边”和“对边”的区别.
要点提醒
1. 相等的元素:两角及其中一角的对边;
2. 用判定三角形全等的方法证明三角形全等时,要注意图形中隐含的等角. 虽然已知条件无涉及,但证明中要特别注意挖掘这些重要条件.
已知:如图1.3-6,AB=AC,AD=AE .求证:△BOD≌△COE.
例 3
解题秘方:找出两个三角形中两组等角及其中一组等角的对边相等,利用“AAS”判定两个三角形全等.
证明:在△ABE和△ACD中,
∴△ABE≌△ACD(SAS).
∴∠B=∠C(全等三角形的对应角相等).
公共角可直接写出,对顶角也可直接写出.
∵ AB=AC,AD=AE(已知),
∴ AB-AD=AC-AE(等量减等量差相等),即BD=CE.
在△BOD和△COE中,
∴△BOD≌△COE(AAS).
教你一招
证明三角形全等时找条件的方法:
证明三角形全等时,有些条件是已知的,有些条件是隐含在题设或图形中的,比如对顶角相等、公共角、公共边等,还有些条件是通过证明其他三角形全等,利用全等三角形的性质得到的.
1. 基本事实 三边分别相等的两个三角形全等(可以简写成“边边边”或“SSS”).
2. 书写格式 如图1.3-7,
在△ABC和△A'B'C'中,
∴△ABC≌△A'B'C'(SSS).
知识点
全等三角形的判定方法——边边边(SSS)
4
要点提醒
1. 相等的元素:三角形的三条边;
2. 在列举两个三角形全等的条件时,应把三个条件按顺序排列并用大括号将其括起来;
3. 书写过程中三角形边的两个端点及三角形的顶点前后顺序要对应.
[二模· 苏州姑苏区] 已知: 如图1.3-8,AC=BD, AD=BC,AD、BC相交于点O,过点O作OE⊥AB,垂足为E.
例 4
求证:(1)△ABC≌△BAD.
解题秘方:紧扣“SSS”找出两个三角形中三边对应相等的条件来证明△ABC≌△BAD;
证明:在△ABC和△BAD中,
∴△ABC≌△BAD(SSS);
(2)AE=BE.
解题秘方:紧扣全等三角形的性质,以及垂直的性质得出两角相等,利用“AAS”证明两个三角形全等可得出结论.
证明:∵△ABC≌△BAD,
∴∠CBA=∠DAB,即∠OAE=∠OBE.
∵ OE⊥AB,∴∠AEO=∠BEO=90°.
在△AEO和△BEO中,
∴△AEO≌△BEO(AAS).∴ AE=BE.
方法点拨
除了题目中已知的边相等以外,还有些相等的边隐含在题设或图形中. 常见的有:
1. 公共边相等;
2. 等边加(或减)等边,其和(或差)仍相等;
3. 由中点得出线段相等.
1. 三角形的稳定性 如果一个三角形三边的长度确定,那么这个三角形的形状和大小就完全确定,这个性质叫做三角形的稳定性. 三角形的稳定性在生活和生产中有着广泛的应用.
2. 四边及四边以上的图形不具有稳定性,为保证其稳定,常在多边形中构造三角形.
知识点
三角形的稳定性
5
[探究题] 要使四边形木架(用四根木条钉成)不易变形,至少要再钉上几根木条?五边形木架呢?六边形木架呢? n边形木架呢?
例 5
解题秘方:若要使多边形稳定, 需将它变换成若干个三角形. 先画出图形,结合图形分割三角形得出:四边形:1 根,五边形:2 根,六边形:3 根,由类比推理可知,n边形:(n-3)根,如图1.3-9 所示.
解:四边形木架至少要再钉上1根木条,五边形木架至少要再钉上2根木条,六边形木架至少要再钉上3根木条,n边形木架至少要再钉上(n-3)根木条.
方法点拨
本题运用了数形结合思想,使问题更直观、易懂,还运用了从特殊到一般的思想,由四边形、五边形、六边形类比推出n边形. 此题为一道规律探究题,通过观察图形,分析、归纳出其中的规律.
1. 角平分线的作法 用直尺和圆规作∠AOB的平分线.
作法:
(1)以点O为圆心,任意长为半径作弧,分别交射线OA、OB于点C、D.
知识点
用尺规作角平分线和垂线
6
(2)分别以点C、D为圆心,大于CD的长为半径作弧,两弧在∠AOB的内部交于点M.
特别解读: “大于CD的长为半径作弧”是因为若以小于CD的长为半径,则画出的两弧不能相交.
(3)作射线OM. OM就是∠AOB的平分线 .(如图1.3-10)
连接CM、DM,依据作图可知△OCM≌△ODM(SSS), 所以∠AOM=∠BOM, 所以OM平分∠ AOB.
2. 垂线的作法
过直线上一点作垂线 1. 以点P为圆心,适当的长为半径作弧,使它与直线l 交于点M、N. 2. 分别以点M、N为圆心,大于MN的长为半径作 弧,两弧交于点C. 3. 作直线CP. 直线CP即为所求. 如图.
续表
过直线 外一点 作垂线 1. 以点C为圆心,适当的长为半径作弧,使它与直线l 交于点A、B. 2. 分别以点A、B为圆心,大于AB的长为半径作弧,两弧交于点D. 3. 作直线CD. 直线CD即为所求. 如图.
特别解读
1. 因为所作的垂线是一条直线,所以不能说成“作射线CP”或者“连接CP”.
2. 根据图,连接CM、CN, 可知△CMP≌△CNP(SSS),所以∠CPM=∠CPN. 又∠CPM+∠CPN=180°,所以 ∠CPM=∠CPN=90 °, 所以直线CP 即为所求作的垂线.
[月考·宜兴] 如图1.3-11,已知△ABC,按下列要求
作图:(尺规作图,保留痕迹不写作法)
例 6
(1)作△ABC的角平分线BE,交AC于点E;
解题秘方:利用作角平分线的方法作图即可;
解:如图1.3-11 所示:
线段BE即为所求;
(2)作BC边上的高AD,垂足为D.
解题秘方:利用过直线外一点,作垂线的方法作图即可.
解:如图1.3-11 所示:
线段AD即为所求.
方法点拨
尺规作图要虚实分明,一般辅助性的线用虚线, 要求画出的线用实线,要保留作图痕迹,这样才可以体现出作图的全过程. 注意本题中求作的三角形的角平分线和高是线段.
定理 斜边和一条直角边分别相等的两个直角三角形全等(可以简写成“斜边、直角边”或“HL”).
知识点
直角三角形全等的判定方法——斜边、直角边(HL)
7
2. 书写格式 如图1.3-12,
在Rt△ABC和Rt△A′B′C′中,
∴ Rt△ABC≌ Rt△A′B′C′(HL).
3. 注意点 书写时必须强调直角三角形.
4. 易错警示 “HL”是判定两个直角三角形全等的特殊方法,但不是唯一方法,前面学习的判定三角形全等的方法在直角三角形中仍然适用.
特别提醒
1. 应用“HL”判定两个直角三角形全等,在书写时一定要加上“Rt”.
2. 判定两个直角三角形全等的特殊方法“HL”, 只适用于直角三角形全等的判定, 对于一般三角形不适用.
已知:如图1.3-13,AC⊥BC,AD⊥BD,垂足分别是点C、D,AD=BC,CE⊥AB,DF⊥AB,垂足分别是点E、F. 求证:CE=DF.
例 7
解题秘方:利用“HL”证明两个直角三角形全等,为证明两条线段相等创造条件.
证明:∵ AC⊥BC,AD⊥BD(已知),
∴∠ACB=∠BDA=90° .
在Rt△ABC和Rt△BAD中,
∴ Rt△ABC≌ Rt△BAD(HL).
∴∠CBE=∠DAF(全等三角形的对应角相等).
∵ CE⊥AB,DF⊥AB(已知),
∴∠CEB=∠DFA=90° .
在△BCE和△ADF中,
∴△BCE≌△ADF(AAS).
∴ CE=DF(全等三角形的对应边相等).
技巧点拨
两个直角三角形中,由于有直角相等的条件,所以判定两个直角三角形全等只需要再找2对对应元素分别相等(其中至少有一对边).
探索三角形全等的条件
一般三角
形全等的
判定方法
SAS
ASA和AAS
SSS
HL
直角三角
形全等的
判定方法
必做: 请完成教材课后练习
补充: 请完成《典中点》《点拨训练》本课时习题
作业1
作业2
知识是力量,
梦想是翅膀。
第1章 全等三角形
1.3 探索三角形全等的条件
1
学习目标
2
课时导入
3
感悟新知
4
随堂检测
5
课堂小结
全等三角形的判定方法——边角边(SAS)
全等三角形的判定方法——角边角(ASA)
全等三角形的判定方法——角角边(AAS)
全等三角形的判定方法——边边边(SSS)
三角形的稳定性
用尺规作角平分线和垂线
直角三角形全等的判定方法——斜边、直角边(HL)
一张教学用的三角形硬纸板不小心被撕坏了,如图,你能制作一张与原来同样大小的新教具?能恢复三角形的原貌吗?
1. 基本事实 两边及其夹角分别相等的两个三角形全等(可以简写成“边角边”或“SAS”).
2. 书写格式 如图1.3-1,
在△ABC和△A'B'C'中 ,
∴△ABC≌△A'B'C‘(SAS).
知识点
全等三角形的判定方法——边角边(SAS)
1
要点提醒
1. 相等的元素:两边及其夹角.
2. 书写顺序:边→角→边.
3. 两边和其中一边的对角分别相等的两个三角形不一定全等.
例 1
[中考·兰州] 如图1.3-2 ①是小军制作的燕子风筝,燕子风筝的骨架图如图1.3-2 ② 所示,AB=AE,AC=AD,∠BAD=∠EAC,∠C=50°,求∠D的大小.
解题秘方:紧扣隐含公共角证明∠ BAC=∠EAD,利用“SAS”证明△BAC ≌△EAD,最后由全等三角形的性质求解.
解:∵∠BAD=∠EAC,
∴∠BAD+∠CAD=∠EAC+∠CAD,
即∠BAC=∠EAD.
在△BAC和△EAD中,
∴△BAC≌△EAD(SAS).∴∠D=∠C=50°.
方法点拨
常见的隐含等角的情况:①公共角相等;②对顶角相等;③等角加(或减)等角,其和(或差)仍相等;④同角或等角的余(或补) 角相等;⑤由角平分线的定义得出角相等;⑥由垂直的定义得出角相等;⑦由平行线得到同位角或内错角相等.
1. 基本事实 两角及其夹边分别相等的两个三角形全等(可以简写成“角边角”或“ASA”).
2. 书写格式 如图1.3-3,在△ABC和△A′B′C′中,
∴△ABC≌△A′B′C′(ASA).
知识点
全等三角形的判定方法——角边角(ASA)
2
要点提醒
1. 相等的元素:两角及其夹边.
2. 书写顺序:角→边→角.
3. 夹边即两个角的公共边.
[期末·杭州] 如图1.3-4,点A、D、C、E在同一条直线上,AB∥EF,AB=EF, ∠B=∠F,AE=10,AC=7,则CD的长为( )
A. 5.5
B. 4
C. 4.5
D. 3
例 2
解题秘方:解题的关键是由平行线得出角相等,构造两角及其夹边对应相等,利用全等三角形的判定与性质求出线段之间的数量关系.
答案:B
解:∵ AB∥EF(已知),
∴∠A=∠E(两直线平行,内错角相等).
在△ABC和△EFD中,
∴△ABC≌△EFD(ASA).
∴ ED=AC=7(全等三角形的对应边相等).
∴ AD=AE-ED=10-7=3.∴ CD=AC-AD=7-3=4.
方法点拨
运用“ASA”判定两个三角形全等,既要找边相等,又要找角相等,除已知条件外,看缺什么条件,就去找什么条件. 另外,判定两个三角形全等后可以运用其性质,得出线段或角的相等关系.
1. 基本事实(ASA)的推论 两角分别相等且其中一组等角的对边相等的两个三角形全等(可以简写成“角角边”或“AAS”).
知识点
全等三角形的判定方法——角角边(AAS)
3
2. 书写格式 如图1.3-5,在△ABC和△A'B'C'中,
∴△ABC≌△A'B'C'(AAS).
3. 特别解读
(1)判定两个三角形全等的三个条件中,“边”是必不可少的;
(2)由于“角角边”和“角边角”是可以互相转化的,故能用“角角边”证明的问题,一般也可以用“角边角”证明;
(3)在运用“ASA”和“AAS”判定时,要注意“夹边”和“对边”的区别.
要点提醒
1. 相等的元素:两角及其中一角的对边;
2. 用判定三角形全等的方法证明三角形全等时,要注意图形中隐含的等角. 虽然已知条件无涉及,但证明中要特别注意挖掘这些重要条件.
已知:如图1.3-6,AB=AC,AD=AE .求证:△BOD≌△COE.
例 3
解题秘方:找出两个三角形中两组等角及其中一组等角的对边相等,利用“AAS”判定两个三角形全等.
证明:在△ABE和△ACD中,
∴△ABE≌△ACD(SAS).
∴∠B=∠C(全等三角形的对应角相等).
公共角可直接写出,对顶角也可直接写出.
∵ AB=AC,AD=AE(已知),
∴ AB-AD=AC-AE(等量减等量差相等),即BD=CE.
在△BOD和△COE中,
∴△BOD≌△COE(AAS).
教你一招
证明三角形全等时找条件的方法:
证明三角形全等时,有些条件是已知的,有些条件是隐含在题设或图形中的,比如对顶角相等、公共角、公共边等,还有些条件是通过证明其他三角形全等,利用全等三角形的性质得到的.
1. 基本事实 三边分别相等的两个三角形全等(可以简写成“边边边”或“SSS”).
2. 书写格式 如图1.3-7,
在△ABC和△A'B'C'中,
∴△ABC≌△A'B'C'(SSS).
知识点
全等三角形的判定方法——边边边(SSS)
4
要点提醒
1. 相等的元素:三角形的三条边;
2. 在列举两个三角形全等的条件时,应把三个条件按顺序排列并用大括号将其括起来;
3. 书写过程中三角形边的两个端点及三角形的顶点前后顺序要对应.
[二模· 苏州姑苏区] 已知: 如图1.3-8,AC=BD, AD=BC,AD、BC相交于点O,过点O作OE⊥AB,垂足为E.
例 4
求证:(1)△ABC≌△BAD.
解题秘方:紧扣“SSS”找出两个三角形中三边对应相等的条件来证明△ABC≌△BAD;
证明:在△ABC和△BAD中,
∴△ABC≌△BAD(SSS);
(2)AE=BE.
解题秘方:紧扣全等三角形的性质,以及垂直的性质得出两角相等,利用“AAS”证明两个三角形全等可得出结论.
证明:∵△ABC≌△BAD,
∴∠CBA=∠DAB,即∠OAE=∠OBE.
∵ OE⊥AB,∴∠AEO=∠BEO=90°.
在△AEO和△BEO中,
∴△AEO≌△BEO(AAS).∴ AE=BE.
方法点拨
除了题目中已知的边相等以外,还有些相等的边隐含在题设或图形中. 常见的有:
1. 公共边相等;
2. 等边加(或减)等边,其和(或差)仍相等;
3. 由中点得出线段相等.
1. 三角形的稳定性 如果一个三角形三边的长度确定,那么这个三角形的形状和大小就完全确定,这个性质叫做三角形的稳定性. 三角形的稳定性在生活和生产中有着广泛的应用.
2. 四边及四边以上的图形不具有稳定性,为保证其稳定,常在多边形中构造三角形.
知识点
三角形的稳定性
5
[探究题] 要使四边形木架(用四根木条钉成)不易变形,至少要再钉上几根木条?五边形木架呢?六边形木架呢? n边形木架呢?
例 5
解题秘方:若要使多边形稳定, 需将它变换成若干个三角形. 先画出图形,结合图形分割三角形得出:四边形:1 根,五边形:2 根,六边形:3 根,由类比推理可知,n边形:(n-3)根,如图1.3-9 所示.
解:四边形木架至少要再钉上1根木条,五边形木架至少要再钉上2根木条,六边形木架至少要再钉上3根木条,n边形木架至少要再钉上(n-3)根木条.
方法点拨
本题运用了数形结合思想,使问题更直观、易懂,还运用了从特殊到一般的思想,由四边形、五边形、六边形类比推出n边形. 此题为一道规律探究题,通过观察图形,分析、归纳出其中的规律.
1. 角平分线的作法 用直尺和圆规作∠AOB的平分线.
作法:
(1)以点O为圆心,任意长为半径作弧,分别交射线OA、OB于点C、D.
知识点
用尺规作角平分线和垂线
6
(2)分别以点C、D为圆心,大于CD的长为半径作弧,两弧在∠AOB的内部交于点M.
特别解读: “大于CD的长为半径作弧”是因为若以小于CD的长为半径,则画出的两弧不能相交.
(3)作射线OM. OM就是∠AOB的平分线 .(如图1.3-10)
连接CM、DM,依据作图可知△OCM≌△ODM(SSS), 所以∠AOM=∠BOM, 所以OM平分∠ AOB.
2. 垂线的作法
过直线上一点作垂线 1. 以点P为圆心,适当的长为半径作弧,使它与直线l 交于点M、N. 2. 分别以点M、N为圆心,大于MN的长为半径作 弧,两弧交于点C. 3. 作直线CP. 直线CP即为所求. 如图.
续表
过直线 外一点 作垂线 1. 以点C为圆心,适当的长为半径作弧,使它与直线l 交于点A、B. 2. 分别以点A、B为圆心,大于AB的长为半径作弧,两弧交于点D. 3. 作直线CD. 直线CD即为所求. 如图.
特别解读
1. 因为所作的垂线是一条直线,所以不能说成“作射线CP”或者“连接CP”.
2. 根据图,连接CM、CN, 可知△CMP≌△CNP(SSS),所以∠CPM=∠CPN. 又∠CPM+∠CPN=180°,所以 ∠CPM=∠CPN=90 °, 所以直线CP 即为所求作的垂线.
[月考·宜兴] 如图1.3-11,已知△ABC,按下列要求
作图:(尺规作图,保留痕迹不写作法)
例 6
(1)作△ABC的角平分线BE,交AC于点E;
解题秘方:利用作角平分线的方法作图即可;
解:如图1.3-11 所示:
线段BE即为所求;
(2)作BC边上的高AD,垂足为D.
解题秘方:利用过直线外一点,作垂线的方法作图即可.
解:如图1.3-11 所示:
线段AD即为所求.
方法点拨
尺规作图要虚实分明,一般辅助性的线用虚线, 要求画出的线用实线,要保留作图痕迹,这样才可以体现出作图的全过程. 注意本题中求作的三角形的角平分线和高是线段.
定理 斜边和一条直角边分别相等的两个直角三角形全等(可以简写成“斜边、直角边”或“HL”).
知识点
直角三角形全等的判定方法——斜边、直角边(HL)
7
2. 书写格式 如图1.3-12,
在Rt△ABC和Rt△A′B′C′中,
∴ Rt△ABC≌ Rt△A′B′C′(HL).
3. 注意点 书写时必须强调直角三角形.
4. 易错警示 “HL”是判定两个直角三角形全等的特殊方法,但不是唯一方法,前面学习的判定三角形全等的方法在直角三角形中仍然适用.
特别提醒
1. 应用“HL”判定两个直角三角形全等,在书写时一定要加上“Rt”.
2. 判定两个直角三角形全等的特殊方法“HL”, 只适用于直角三角形全等的判定, 对于一般三角形不适用.
已知:如图1.3-13,AC⊥BC,AD⊥BD,垂足分别是点C、D,AD=BC,CE⊥AB,DF⊥AB,垂足分别是点E、F. 求证:CE=DF.
例 7
解题秘方:利用“HL”证明两个直角三角形全等,为证明两条线段相等创造条件.
证明:∵ AC⊥BC,AD⊥BD(已知),
∴∠ACB=∠BDA=90° .
在Rt△ABC和Rt△BAD中,
∴ Rt△ABC≌ Rt△BAD(HL).
∴∠CBE=∠DAF(全等三角形的对应角相等).
∵ CE⊥AB,DF⊥AB(已知),
∴∠CEB=∠DFA=90° .
在△BCE和△ADF中,
∴△BCE≌△ADF(AAS).
∴ CE=DF(全等三角形的对应边相等).
技巧点拨
两个直角三角形中,由于有直角相等的条件,所以判定两个直角三角形全等只需要再找2对对应元素分别相等(其中至少有一对边).
探索三角形全等的条件
一般三角
形全等的
判定方法
SAS
ASA和AAS
SSS
HL
直角三角
形全等的
判定方法
必做: 请完成教材课后练习
补充: 请完成《典中点》《点拨训练》本课时习题
作业1
作业2
知识是力量,
梦想是翅膀。
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
