苏科版数学八年级上册2.5 等腰三角形的轴对称性 课件(共59张PPT)
文档属性
| 名称 | 苏科版数学八年级上册2.5 等腰三角形的轴对称性 课件(共59张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-28 14:58:32 | ||
图片预览









文档简介
(共59张PPT)
第2章 轴对称图形
2.5 等腰三角形的轴对称性
等腰三角形的性质
等腰三角形的判定
等边三角形的定义及性质
等边三角形的判定
直角三角形斜边上的中线的性质
看到下面三角形了吗,它有何特点呢?
我们今天来探讨一下等腰三角形的性质.
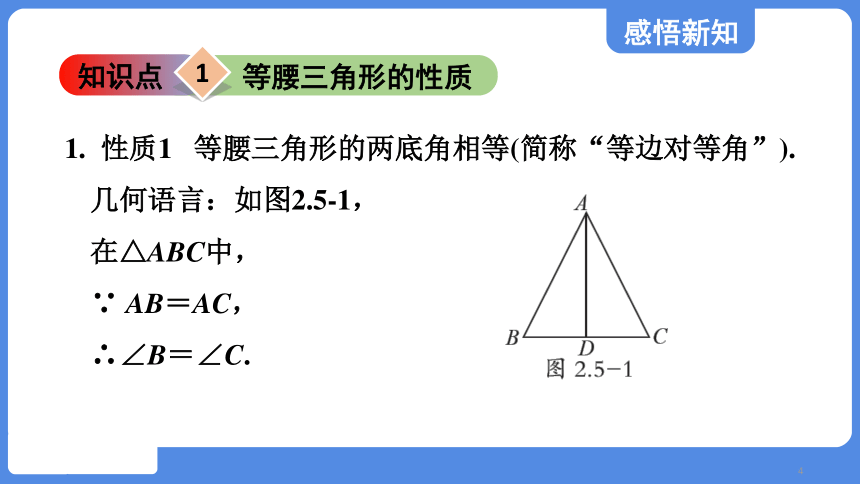
1. 性质1 等腰三角形的两底角相等(简称“等边对等角”).
几何语言:如图2.5-1,
在△ABC中,
∵ AB=AC,
∴∠B=∠C.
知识点
等腰三角形的性质
1
2. 性质2 等腰三角形底边上的高线、中线及顶角
平分线重合(简称“三线合一”).
如图2.5-1,在△ABC中,
(1)∵ AB=AC,AD⊥BC,
∴ AD平分∠BAC,BD=DC.
(2)∵ AB=AC,BD=DC,∴ AD⊥BC,AD平分∠BAC.
(3)∵ AB=AC,AD平分∠BAC,
∴ BD=DC,AD⊥BC.
3. 对称性 等腰三角形是轴对称图形,顶角平分线(或底边上的高线、底边上的中线)所在的直线是它的对称轴.
特别提醒
作用: 是证明角相等的常用方法, 应用它证角相等时可省去三角形全等的证明,因而更简便.
特别解读
(1)这里的“ 线”是一条线段, 给出一线的名称, 可以得出其他两线的名称.
(2)作用: 是证明线段相等、角相等、线段垂直等关系的重要方法.
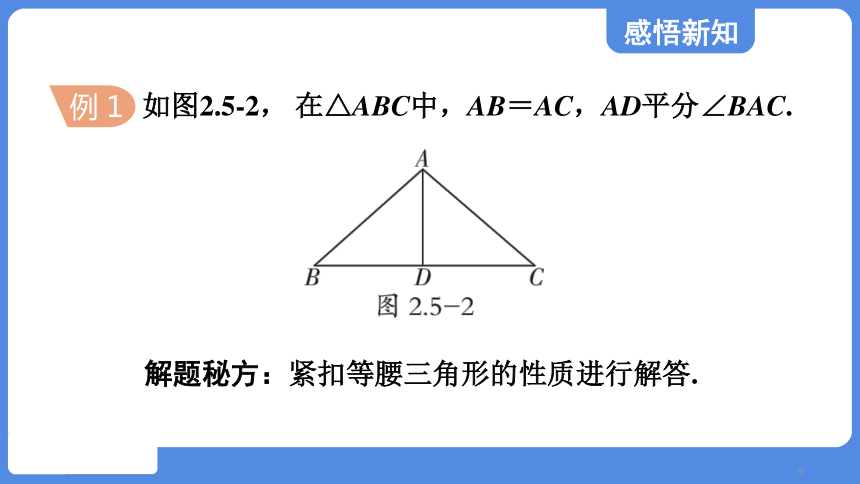
例 1
如图2.5-2, 在△ABC中,AB=AC,AD平分∠BAC.
解题秘方:紧扣等腰三角形的性质进行解答.
(1)求∠ADB的度数;
(2)若∠BAC=100°,求∠B、∠C的度数;
解:∵ AB=AC,AD平分∠BAC,
∴ AD⊥BC,∴∠ADB=90° .
在△ABC中,∵ AB=AC,∠BAC=100°,
∴ ∠B=∠C=×(180 °-∠BAC)=×(180 °-100°)=40°.
解:∵ AB=AC,AD平分∠BAC,
∴ AD是BC边上的中线,
∴ BD=BC=×3=1.5(cm),
即BD的长是1.5 cm.
(3)若BC=3 cm,求BD的长.
特别提醒
(1)在等腰三角形中,运用“三线合一”时,已知其中“一线”,就可以得到另外“两线”. 根据等腰三角形的“三线合一”的性质可以得到等线段、等角以及两条线段互相垂直.
(2)“等边对等角”的前提是在同一个三角形中.
1. 判定定理 有两个角相等的三角形是等腰三角形(简称“等角对等边”).
几何语言:在△ABC中,
∵∠B=∠C,∴ AB=AC.
知识点
等腰三角形的判定
2
2. 等腰三角形的性质与判定的异同
相同点:使用的前提都是“在同一个三角形中”;
不同点: 由三角形的两边相等,得到它们所对的角相等,是等腰三角形的性质;由三角形的两角相等,得到它是等腰三角形,是等腰三角形的判定. 即
等腰三角形的性质:两边相等→这两边所对的角相等;
等腰三角形的判定:两角相等→这两角所对的边相等.
3. 拓展
根据等腰三角形的性质定理和判定定理是互逆定理可知,由等腰三角形的“三线合一”性质的逆命题可得出等腰三角形的三个判定方法:
(1)三角形中一边上的中线和高线重合时,利用线段的垂直平分线定理可以判定该三角形为等腰三角形;
(2)三角形中一边上的中线和对角的平分线重合时,利用三角形全等可以判定该三角形为等腰三角形;
(3)三角形中一边上的高线和对角的平分线重合时,直接利用三角形全等可以判定该三角形为等腰三角形.
特别提醒
(1)“ 等角对等边” 不能叙述为“ 如果一个三角形有两个底角相等, 那么它的两条腰相等”, 因为在未判定出它是等腰三角形之前, 不能用“ 底角” “ 顶角” “ 腰” “ 底边” 这些名词.
特别提醒
(2)“等角对等边”是我们以后证明两条线段相等的常用方法,在证明过程中,经常通过计算三角形各角的度数,或利用角之间的关系得到角相等,从而得到所对的边相等.
[期末·朝阳区] 如图2.5-3, 在△ABC中,AD平分∠BAC,BD⊥AD于点D,过点D作DE∥AC交AB于点E.求证:E为AB的中点.
例 2
解题秘方:利用“等角对等边”判定等腰三角形,只需证明三角形两个内角相等即可.
证明:∵ AD平分∠BAC,∴∠BAD=∠CAD.
∵ DE∥AC,∴∠CAD=∠ADE.
∴∠BAD=∠ADE.∴ AE=DE.
∵ AD⊥DB,∴∠ADB=90°.
∴∠EAD+∠ ABD=90°,
∠ADE+∠BDE=∠ADB=90°,
∴∠ABD=∠BDE.∴ BE=DE=AE. ∴ E为AB的中点.
方法点拨
本题包括两个模型:(1)由“角平分线+ 平行线” 推出“等腰三角形”,实际上由“①角平分线,②平行线,③等腰三角形”三个结论中两个可以推出另一个成立;(2)由 “直角三角形+ 等腰三角形”推出“斜边中点”, 实际上由“①直角三角形,②等腰三角形,③斜边中点”三个结论中两个可以推出另一个成立.
1. 定义 三边相等的三角形叫做等边三角形或正三角形.
2. 性质
(1)等边三角形的三条边都相等;
(2)等边三角形的三个内角都相等,并且每一个角都等于60°;
知识点
等边三角形的定义及性质
3
(3)等边三角形是轴对称图形,它有3 条对称轴,分别为三边的垂直平分线;
(4)各边上的高线、中线、对应的角平分线重合,且长度相等.
特别解读
等边三角形是特殊的等腰三角形,具备等腰三角形的所有性质:
(1)任意两边都可以作为腰;
(2)任意一个角都可以作为顶角;
(3)任意一边上都有“三线合一”.
如图2.5-4,△ABC是等边三角形,D、E、F分别是边AB、AC、BC上的点,且DE⊥AC、EF⊥BC、FD⊥AB,计算△DEF各个内角的度数.
例 3
解题秘方:紧扣等边三角形的三个内角都等于60°,求角的度数.
解:∵△ABC是等边三角形,∴∠A=∠B=∠C=60° .
∵ DE⊥AC,EF⊥BC,FD⊥AB,
∴∠AED=∠EFC=∠FDB=90°,
∴∠ADE=90°-∠A=90°-60°=30°,
∴∠EDF=180°-∠ADE-∠FDB=180°-30°-90°=60°. 同理可得∠DEF=∠EFD=60° .
∴△DEF各个内角的度数都是60° .
解法提醒
等边三角形的三个内角都等于60°,为三角形的内角直接提供了角的条件. 若同时要运用三个内角, 只需以一个角为例计算,其余可同理得到.
如图2.5-5,等边三角形ABC的边长为3,D是AC的中点,点E在BC的延长线上. 若DE=DB,求CE的长.
解题秘方:利用等边三角形“三线合一”的性质将未知线段向已知线段转化.
例 4
解:∵等边三角形ABC的边长是3,
∴∠ABC=∠ACB=60°,AC=3.
∵ D是AC的中点,
∴ CD=AC=1.5,∠DBE=∠ABC=30°.
∵ DE=DB,∴∠DEC=∠DBE=30°.
∵∠ACB=60°,∴∠CDE=∠ACB-∠DEC=30°,
∴∠CDE=∠DEC,∴ CE=CD=1.5,即CE的长是1.5.
方法点拨
等边三角形的任何一边上都有“三线合一”的性质,有时要运用的和已知的不一致,需要通过“三线合一”的性质将未知线段向已知线段转化.
1. 判定定理1 三个角都相等的三角形是等边三角形.
几何语言:如图2.5-6,在△ABC中,
∵∠A=∠B=∠C,
∴△ABC是等边三角形.
知识点
等边三角形的判定
4
2. 判定定理2 有一个角是60°的等腰三角形是等边三角形.
几何语言:如图2.5-6,在△ABC中,
∵ AB=AC,∠A=60°
(或∠B=60°或∠C=60°),
∴△ABC是等边三角形.
证明等边三角形的思维导图:
三角形
思路1:三边相等
思路2:三角相等
等边三角形
三角形
等腰三角
形的判定
等腰三角形
有一个角等于60°
等边三角形
特别解读
(1)在等腰三角形中,只要有一个角是60 °,无论这个角是顶角还是底角,判定定理2都成立.
(2)等边三角形的判定方法:
①若已知三边关系,一般选用定义判定;
②若已知三角关系,一般选用判定定理1判定;
③若已知三角形是等腰三角形,一般选用判定定理2判定.
如图2.5-7, 在等边三角形ABC中, ∠ABC和∠ACB的平分线相交于点O,OB、OC的垂直平分线分别交BC于点E、F,连接OE、OF.
求证:△OEF是等边三角形.
例 5
解题秘方:利用等边三角形的判定定理1, 通过求∠OEF=∠OFE=∠EOF=60°,得到△OEF是等边三角形.
证明:∵△ABC是等边三角形,
∴∠ABC=∠ACB=60° .
∵ CO、BO分别平分∠ACB、∠ABC,
∴∠OBE=∠OCF=30° .
∵ OB、OC的垂直平分线分别交BC于点E、F,
∴ OE=BE,OF=CF,
∴∠BOE=∠OBE=30°,∠COF=∠OCF=30° .
∴∠OEF=∠BOE+∠OBE=60°,
∠OFE=∠COF+∠OCF=60° .
∴∠EOF=180°-∠OEF-∠OFE=60°,
∴△OEF是等边三角形.
教你一招
(1)从角的角度证明三角形是等边三角形的两条思路:
一是证明三角形的三个内角相等;
二是求出三角形的三个内角的度数都是60° .
(2)在已知的等边三角形内部判定某个三角形是等边三角形时,原等边三角形的三个内角为60°,为求新等边三角形的内角度数提供了条件.
如图2.5-8,C为线段AB上一点, △ACM和△CBN都是等边三角形,AN、MC相交于点E,BM、CN相交于点F. 求证:
例 6
(1)AN=MB;
解题秘方:要证AN=MB,只需证△ACN ≌△MCB;
证明:∵△ACM和△CBN都是等边三角形,
∴ AC=MC,CN=CB,∠ACM=∠BCN=60° .
∴∠ACM+∠MCN=∠BCN+∠MCN,
即∠ACN=∠MCB.
在△ACN和△MCB中,
∴△ACN≌△MCB,∴ AN=MB.
(2)△CEF是等边三角形.
解题秘方:根据已知条件, 易求∠ ECF=60°,故证明△ECF为等腰三角形即可.
证明:∵△ACN≌△MCB,∴∠ENC=∠FBC.
∵∠ECN=180°-∠ACM-∠NCB=60°,
∴∠ECN=∠FCB.
在△ECN和△FCB中,
∴△ECN≌△FCB,∴CE=CF.
又∵∠ECF=60°,∴△CEF是等边三角形.
另解
∵△ACN≌△MCB,∴∠CAE=∠CMF.
∵∠MCF=180° -∠ACM-∠NCB=60°,
∴∠ACE=∠MCF.
在△ACE和△MCF中,
∴△ACE ≌△MCF,∴ CE=CF.
1. 性质 直角三角形斜边上的中线等于斜边的一半.
几何语言:如图2.5-9,在Rt△ABC中,
∵∠ACB=90°,D为AB的中点,
∴ CD=AB.
知识点
直角三角形斜边上的中线的性质
5
(1)在直角三角形中,有斜边上的中点,通常考虑运用这一性质解题.
(2)根据性质可知直角三角形斜边上的中线将直角三角形分成两个等腰三角形.
特别提醒
此性质在填空和选择题中可以直接应用,在解答题中需要取斜边上的中线,构造等腰三角形证明线段的倍分关系和计算角的度数.
2. 易错警示 在△ABC中,D为AB的中点, 不能得出CD=AB,前提是∠ACB=90°
3. 拓展 含30°角的直角三角形的性质
在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半.
几何语言:如图2.5-10,在Rt△ABC中,
∵∠C=90°,∠A=30°,
∴ BC=AB.
特别警示
应用含30°角的直角三角形的性质是求线段长度和证明线段倍分关系的重要方法.
[中考·淮安] 如图2.5-11,在△ABC中,AB=AC,∠BAC的平分线交BC于点D,E为AC的中点,若 AB=10,则DE的长是( )
A. 8
B. 6
C. 5
D. 4
例 7
解题秘方:先利用等腰三角形的“三线合一”性质得出AD⊥ BC,再由直角三角形斜边中线的性质可求出DE的长.
解:∵ AB=AC=10,AD平分∠BAC,
∴ AD⊥BC,∴∠ADC=90°.
在Rt△ADC中,∵ E为AC的中点,∴ DE=AC=5.
答案:C
方法点拨
可以运用“ 直角三角形斜边上的中线等于斜边的一半” 解决的问题往往具有两个明显特征:一是有直角(直角三角形或待证明的直角),二是有中点(斜边上的中线).
等腰
三角形
两边相等
性质
等边对等角
三线合一
判定
等角对等边
三线中的二线合一
互逆
等边
三角形
判定
性质
必做: 请完成教材课后练习
补充: 请完成《典中点》《点拨训练》本课时习题
作业1
作业2
知识是力量,
梦想是翅膀。
第2章 轴对称图形
2.5 等腰三角形的轴对称性
等腰三角形的性质
等腰三角形的判定
等边三角形的定义及性质
等边三角形的判定
直角三角形斜边上的中线的性质
看到下面三角形了吗,它有何特点呢?
我们今天来探讨一下等腰三角形的性质.
1. 性质1 等腰三角形的两底角相等(简称“等边对等角”).
几何语言:如图2.5-1,
在△ABC中,
∵ AB=AC,
∴∠B=∠C.
知识点
等腰三角形的性质
1
2. 性质2 等腰三角形底边上的高线、中线及顶角
平分线重合(简称“三线合一”).
如图2.5-1,在△ABC中,
(1)∵ AB=AC,AD⊥BC,
∴ AD平分∠BAC,BD=DC.
(2)∵ AB=AC,BD=DC,∴ AD⊥BC,AD平分∠BAC.
(3)∵ AB=AC,AD平分∠BAC,
∴ BD=DC,AD⊥BC.
3. 对称性 等腰三角形是轴对称图形,顶角平分线(或底边上的高线、底边上的中线)所在的直线是它的对称轴.
特别提醒
作用: 是证明角相等的常用方法, 应用它证角相等时可省去三角形全等的证明,因而更简便.
特别解读
(1)这里的“ 线”是一条线段, 给出一线的名称, 可以得出其他两线的名称.
(2)作用: 是证明线段相等、角相等、线段垂直等关系的重要方法.
例 1
如图2.5-2, 在△ABC中,AB=AC,AD平分∠BAC.
解题秘方:紧扣等腰三角形的性质进行解答.
(1)求∠ADB的度数;
(2)若∠BAC=100°,求∠B、∠C的度数;
解:∵ AB=AC,AD平分∠BAC,
∴ AD⊥BC,∴∠ADB=90° .
在△ABC中,∵ AB=AC,∠BAC=100°,
∴ ∠B=∠C=×(180 °-∠BAC)=×(180 °-100°)=40°.
解:∵ AB=AC,AD平分∠BAC,
∴ AD是BC边上的中线,
∴ BD=BC=×3=1.5(cm),
即BD的长是1.5 cm.
(3)若BC=3 cm,求BD的长.
特别提醒
(1)在等腰三角形中,运用“三线合一”时,已知其中“一线”,就可以得到另外“两线”. 根据等腰三角形的“三线合一”的性质可以得到等线段、等角以及两条线段互相垂直.
(2)“等边对等角”的前提是在同一个三角形中.
1. 判定定理 有两个角相等的三角形是等腰三角形(简称“等角对等边”).
几何语言:在△ABC中,
∵∠B=∠C,∴ AB=AC.
知识点
等腰三角形的判定
2
2. 等腰三角形的性质与判定的异同
相同点:使用的前提都是“在同一个三角形中”;
不同点: 由三角形的两边相等,得到它们所对的角相等,是等腰三角形的性质;由三角形的两角相等,得到它是等腰三角形,是等腰三角形的判定. 即
等腰三角形的性质:两边相等→这两边所对的角相等;
等腰三角形的判定:两角相等→这两角所对的边相等.
3. 拓展
根据等腰三角形的性质定理和判定定理是互逆定理可知,由等腰三角形的“三线合一”性质的逆命题可得出等腰三角形的三个判定方法:
(1)三角形中一边上的中线和高线重合时,利用线段的垂直平分线定理可以判定该三角形为等腰三角形;
(2)三角形中一边上的中线和对角的平分线重合时,利用三角形全等可以判定该三角形为等腰三角形;
(3)三角形中一边上的高线和对角的平分线重合时,直接利用三角形全等可以判定该三角形为等腰三角形.
特别提醒
(1)“ 等角对等边” 不能叙述为“ 如果一个三角形有两个底角相等, 那么它的两条腰相等”, 因为在未判定出它是等腰三角形之前, 不能用“ 底角” “ 顶角” “ 腰” “ 底边” 这些名词.
特别提醒
(2)“等角对等边”是我们以后证明两条线段相等的常用方法,在证明过程中,经常通过计算三角形各角的度数,或利用角之间的关系得到角相等,从而得到所对的边相等.
[期末·朝阳区] 如图2.5-3, 在△ABC中,AD平分∠BAC,BD⊥AD于点D,过点D作DE∥AC交AB于点E.求证:E为AB的中点.
例 2
解题秘方:利用“等角对等边”判定等腰三角形,只需证明三角形两个内角相等即可.
证明:∵ AD平分∠BAC,∴∠BAD=∠CAD.
∵ DE∥AC,∴∠CAD=∠ADE.
∴∠BAD=∠ADE.∴ AE=DE.
∵ AD⊥DB,∴∠ADB=90°.
∴∠EAD+∠ ABD=90°,
∠ADE+∠BDE=∠ADB=90°,
∴∠ABD=∠BDE.∴ BE=DE=AE. ∴ E为AB的中点.
方法点拨
本题包括两个模型:(1)由“角平分线+ 平行线” 推出“等腰三角形”,实际上由“①角平分线,②平行线,③等腰三角形”三个结论中两个可以推出另一个成立;(2)由 “直角三角形+ 等腰三角形”推出“斜边中点”, 实际上由“①直角三角形,②等腰三角形,③斜边中点”三个结论中两个可以推出另一个成立.
1. 定义 三边相等的三角形叫做等边三角形或正三角形.
2. 性质
(1)等边三角形的三条边都相等;
(2)等边三角形的三个内角都相等,并且每一个角都等于60°;
知识点
等边三角形的定义及性质
3
(3)等边三角形是轴对称图形,它有3 条对称轴,分别为三边的垂直平分线;
(4)各边上的高线、中线、对应的角平分线重合,且长度相等.
特别解读
等边三角形是特殊的等腰三角形,具备等腰三角形的所有性质:
(1)任意两边都可以作为腰;
(2)任意一个角都可以作为顶角;
(3)任意一边上都有“三线合一”.
如图2.5-4,△ABC是等边三角形,D、E、F分别是边AB、AC、BC上的点,且DE⊥AC、EF⊥BC、FD⊥AB,计算△DEF各个内角的度数.
例 3
解题秘方:紧扣等边三角形的三个内角都等于60°,求角的度数.
解:∵△ABC是等边三角形,∴∠A=∠B=∠C=60° .
∵ DE⊥AC,EF⊥BC,FD⊥AB,
∴∠AED=∠EFC=∠FDB=90°,
∴∠ADE=90°-∠A=90°-60°=30°,
∴∠EDF=180°-∠ADE-∠FDB=180°-30°-90°=60°. 同理可得∠DEF=∠EFD=60° .
∴△DEF各个内角的度数都是60° .
解法提醒
等边三角形的三个内角都等于60°,为三角形的内角直接提供了角的条件. 若同时要运用三个内角, 只需以一个角为例计算,其余可同理得到.
如图2.5-5,等边三角形ABC的边长为3,D是AC的中点,点E在BC的延长线上. 若DE=DB,求CE的长.
解题秘方:利用等边三角形“三线合一”的性质将未知线段向已知线段转化.
例 4
解:∵等边三角形ABC的边长是3,
∴∠ABC=∠ACB=60°,AC=3.
∵ D是AC的中点,
∴ CD=AC=1.5,∠DBE=∠ABC=30°.
∵ DE=DB,∴∠DEC=∠DBE=30°.
∵∠ACB=60°,∴∠CDE=∠ACB-∠DEC=30°,
∴∠CDE=∠DEC,∴ CE=CD=1.5,即CE的长是1.5.
方法点拨
等边三角形的任何一边上都有“三线合一”的性质,有时要运用的和已知的不一致,需要通过“三线合一”的性质将未知线段向已知线段转化.
1. 判定定理1 三个角都相等的三角形是等边三角形.
几何语言:如图2.5-6,在△ABC中,
∵∠A=∠B=∠C,
∴△ABC是等边三角形.
知识点
等边三角形的判定
4
2. 判定定理2 有一个角是60°的等腰三角形是等边三角形.
几何语言:如图2.5-6,在△ABC中,
∵ AB=AC,∠A=60°
(或∠B=60°或∠C=60°),
∴△ABC是等边三角形.
证明等边三角形的思维导图:
三角形
思路1:三边相等
思路2:三角相等
等边三角形
三角形
等腰三角
形的判定
等腰三角形
有一个角等于60°
等边三角形
特别解读
(1)在等腰三角形中,只要有一个角是60 °,无论这个角是顶角还是底角,判定定理2都成立.
(2)等边三角形的判定方法:
①若已知三边关系,一般选用定义判定;
②若已知三角关系,一般选用判定定理1判定;
③若已知三角形是等腰三角形,一般选用判定定理2判定.
如图2.5-7, 在等边三角形ABC中, ∠ABC和∠ACB的平分线相交于点O,OB、OC的垂直平分线分别交BC于点E、F,连接OE、OF.
求证:△OEF是等边三角形.
例 5
解题秘方:利用等边三角形的判定定理1, 通过求∠OEF=∠OFE=∠EOF=60°,得到△OEF是等边三角形.
证明:∵△ABC是等边三角形,
∴∠ABC=∠ACB=60° .
∵ CO、BO分别平分∠ACB、∠ABC,
∴∠OBE=∠OCF=30° .
∵ OB、OC的垂直平分线分别交BC于点E、F,
∴ OE=BE,OF=CF,
∴∠BOE=∠OBE=30°,∠COF=∠OCF=30° .
∴∠OEF=∠BOE+∠OBE=60°,
∠OFE=∠COF+∠OCF=60° .
∴∠EOF=180°-∠OEF-∠OFE=60°,
∴△OEF是等边三角形.
教你一招
(1)从角的角度证明三角形是等边三角形的两条思路:
一是证明三角形的三个内角相等;
二是求出三角形的三个内角的度数都是60° .
(2)在已知的等边三角形内部判定某个三角形是等边三角形时,原等边三角形的三个内角为60°,为求新等边三角形的内角度数提供了条件.
如图2.5-8,C为线段AB上一点, △ACM和△CBN都是等边三角形,AN、MC相交于点E,BM、CN相交于点F. 求证:
例 6
(1)AN=MB;
解题秘方:要证AN=MB,只需证△ACN ≌△MCB;
证明:∵△ACM和△CBN都是等边三角形,
∴ AC=MC,CN=CB,∠ACM=∠BCN=60° .
∴∠ACM+∠MCN=∠BCN+∠MCN,
即∠ACN=∠MCB.
在△ACN和△MCB中,
∴△ACN≌△MCB,∴ AN=MB.
(2)△CEF是等边三角形.
解题秘方:根据已知条件, 易求∠ ECF=60°,故证明△ECF为等腰三角形即可.
证明:∵△ACN≌△MCB,∴∠ENC=∠FBC.
∵∠ECN=180°-∠ACM-∠NCB=60°,
∴∠ECN=∠FCB.
在△ECN和△FCB中,
∴△ECN≌△FCB,∴CE=CF.
又∵∠ECF=60°,∴△CEF是等边三角形.
另解
∵△ACN≌△MCB,∴∠CAE=∠CMF.
∵∠MCF=180° -∠ACM-∠NCB=60°,
∴∠ACE=∠MCF.
在△ACE和△MCF中,
∴△ACE ≌△MCF,∴ CE=CF.
1. 性质 直角三角形斜边上的中线等于斜边的一半.
几何语言:如图2.5-9,在Rt△ABC中,
∵∠ACB=90°,D为AB的中点,
∴ CD=AB.
知识点
直角三角形斜边上的中线的性质
5
(1)在直角三角形中,有斜边上的中点,通常考虑运用这一性质解题.
(2)根据性质可知直角三角形斜边上的中线将直角三角形分成两个等腰三角形.
特别提醒
此性质在填空和选择题中可以直接应用,在解答题中需要取斜边上的中线,构造等腰三角形证明线段的倍分关系和计算角的度数.
2. 易错警示 在△ABC中,D为AB的中点, 不能得出CD=AB,前提是∠ACB=90°
3. 拓展 含30°角的直角三角形的性质
在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半.
几何语言:如图2.5-10,在Rt△ABC中,
∵∠C=90°,∠A=30°,
∴ BC=AB.
特别警示
应用含30°角的直角三角形的性质是求线段长度和证明线段倍分关系的重要方法.
[中考·淮安] 如图2.5-11,在△ABC中,AB=AC,∠BAC的平分线交BC于点D,E为AC的中点,若 AB=10,则DE的长是( )
A. 8
B. 6
C. 5
D. 4
例 7
解题秘方:先利用等腰三角形的“三线合一”性质得出AD⊥ BC,再由直角三角形斜边中线的性质可求出DE的长.
解:∵ AB=AC=10,AD平分∠BAC,
∴ AD⊥BC,∴∠ADC=90°.
在Rt△ADC中,∵ E为AC的中点,∴ DE=AC=5.
答案:C
方法点拨
可以运用“ 直角三角形斜边上的中线等于斜边的一半” 解决的问题往往具有两个明显特征:一是有直角(直角三角形或待证明的直角),二是有中点(斜边上的中线).
等腰
三角形
两边相等
性质
等边对等角
三线合一
判定
等角对等边
三线中的二线合一
互逆
等边
三角形
判定
性质
必做: 请完成教材课后练习
补充: 请完成《典中点》《点拨训练》本课时习题
作业1
作业2
知识是力量,
梦想是翅膀。
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
