六年级下册数学冀教版圆柱和圆锥整理复习(课件)(共31张PPT)
文档属性
| 名称 | 六年级下册数学冀教版圆柱和圆锥整理复习(课件)(共31张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 976.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-28 00:00:00 | ||
图片预览









文档简介
(共31张PPT)
整理复习第四单元
2022.4.6
一、圆柱
侧面积=底面周长×高=Ch=Πdh=2Πrh
表面积=侧面积+ 2×底面积
=Ch+2Πr =Πdh+2Πr =2Πrh+2Πr
区别
1.意义
2.测量数据
3.单位
体积=底面积×高=Πr h
容积=底面积×高=Πr h
相同点
计算公式
1.侧面积
2.表面积
3.体积、容积
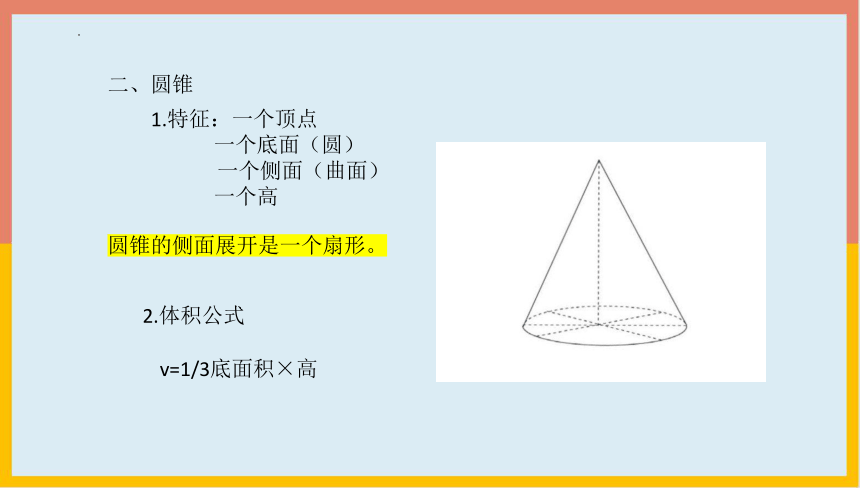
二、圆锥
2.体积公式
1.特征:一个顶点
一个底面(圆)
一个侧面(曲面)
一个高
v=1/3底面积×高
圆锥的侧面展开是一个扇形。
三、常见题型
1.表面积的变化
(1)平行横截面切(切成几个小圆柱)
把一长为1.6分米的圆柱截成3段后,表面积增加了9.6平方米,求圆柱原来的体积?
9.6÷4×0.16
=2.4×0.16
=0.384(立方米)
切成3段,切了两下,切一下多两个底面积,所以四个底面积是9.6
三、常见题型
1.表面积的变化
(2)沿着直径向下切
把长为20分米的圆柱沿着底面直径劈开,表面积增加了80平方分米,求该圆柱原来的表面积是多少?
多的是两个长方形面积
长为d 宽为h(h=d时为正方形)
2dh=80
d=2
r=1
S=3.14×1×1×2+3.14×2×20
=131.88(平方分米)
三、常见题型
1.表面积的变化
(3)高的变化
一个圆柱的底面直径是10厘米,如果高增加2厘米,它的侧面积增加( )平方厘米.
A.31.4 B.62.8 C.157 D.20
B
表面积增加的是高为2 的圆柱的侧面积,体积增加的是高为2 的圆柱的体积。
三、常见题型
1.表面积的变化
(4)拼成近似长方体
一个圆柱拼成近似长方体表面积增加100,圆柱的半径是10,求圆柱的体积
增加的是两个长方形的面积(长为r,宽为h,当r=h时,是正方形)
2rh=100
h=5
V=3.14×10×10×5
三、常见题型
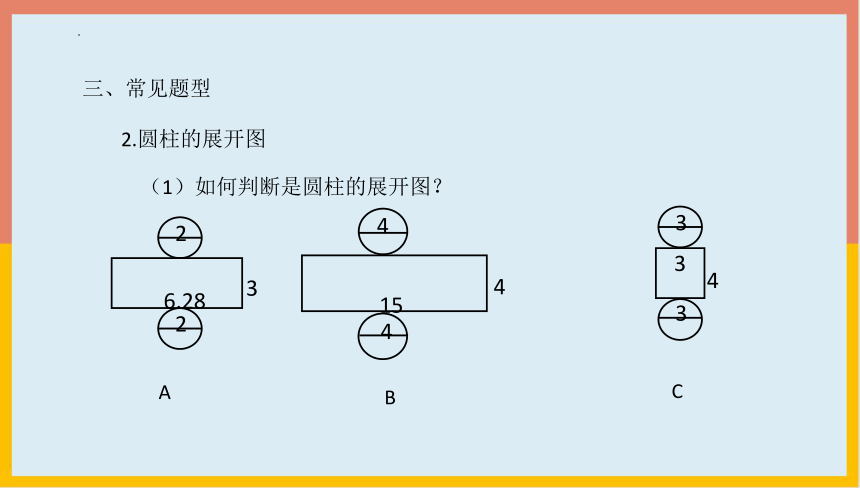
2.圆柱的展开图
(1)如何判断是圆柱的展开图?
2
6.28
2
4
15
4
3
3
3
3
4
4
A
B
C
三、常见题型
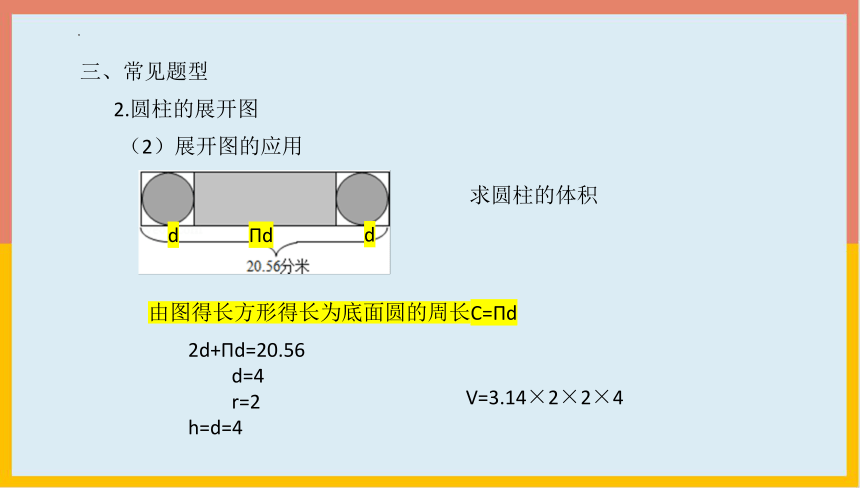
(2)展开图的应用
求圆柱的体积
由图得长方形得长为底面圆的周长C=Πd
Πd
d
d
2d+Πd=20.56
d=4
r=2
h=d=4
V=3.14×2×2×4
2.圆柱的展开图
一个圆柱的底面半径是2厘米,高是2厘米,如果沿高剪开,它的侧面展开图是( )形,这个图形的周长是( )厘米,面积是( )平方厘米。
(2)展开图的应用
周长为侧面展开图(长方形的周长),面积为长方形的面积,相当于圆柱的侧面积
长=底面周长C,宽为高h
周长=(C+h)×2
=(2×3.14×2+2)×2
=29.12
面积=Ch
=2×3.14×2×2
=25.12
2.圆柱的展开图
三、常见题型
(3)正方形侧面展开图
C=Πd=2Πr=h
1.一个圆柱的侧面展开图是一个正方形,这个圆柱的高与底面半径的比是( )。
A.2π∶1 B.1∶π C.π∶1 D.1∶2π
2.一张正方形的纸围成的圆柱,它的底面积和侧面积的比是( )。
A.π∶1 B.1∶π C.1∶4π D.4π∶1
A
C
三、常见题型
2.圆柱的展开图
3.实际应用
(1)压路机
压路机的前轮是圆柱形,它的宽是2米,前轮的底面半径是6分米,如果压路机的前轮每分钟转10周,那么它10分钟压路的面积是多少平方米?
753.6平方米
三、常见题型
3.实际应用
(2)压路机变形
如图所示,圆柱形石碾的底面直径和高都是1米。石碾从A墙滚动到B墙,它碾过的地面面积是多少平方米
4平方米
三、常见题型
3.实际应用
(3)彩带
用丝带捆扎一个圆柱形蛋糕盒(如图),打结用去20cm。捆扎这个蛋糕盒用去丝带多少厘米?
280厘米
三、常见题型
3.实际应用
(4)大棚
王伯伯要在一块地里搭建一个半圆柱形的蔬菜大棚(示意图如下),这块地长24米,宽5米,其中埋入地下部分的塑料薄膜的面积为35平方米,搭建这个蔬菜大棚至少要用多少平方米的塑料薄膜?(蔬菜大棚要将这块地完全覆盖)
243.025平方米
三、常见题型
4.长方形“变”圆柱
三、常见题型
(1)绕长旋转
长为高h,宽为半径r
4.长方形“变”圆柱
三、常见题型
(2)绕宽旋转
宽为高h,长为半径r
4.长方形“变”圆柱
三、常见题型
(3)以长为底面周长围成圆柱
宽为高h,长=底面周长
4.长方形“变”圆柱
三、常见题型
(4)以宽为底面周长围成圆柱
长为高h,宽=底面周长
三、常见题型
5.体积的变化
(1).半径扩大2倍,高不变,体积()
(2).底面积扩大2倍,高不变,体积()
(3).半径不变,高扩大2倍,体积()
(4).半径扩大3,高扩大2倍,体积()
体积=底面积×高=Πr h
6.求不规则物体的体积(容积)
(1)一个圆柱形鱼缸,如下图,把鱼缸中的鱼取出后,水面下降了2厘米,这条鱼的体积是多少?
r=25 2=12.5(厘米)
V=3.14×12.5×12.5×2
=981.25(立方厘米)
三、常见题型
(2)一个密封的瓶子里装着一些水,如图所示。已知瓶子的内底面积为15cm ,瓶子的容积是( )mL。
90
6.求不规则物体的体积(容积)
三、常见题型
(3)按下述步骤测量一颗玻璃球的体积:
①将400mL水倒入一个容积为500mL的烧杯中;
②将4颗相同的玻璃球放入水中,结果水还不满;
③再将1颗同样的玻璃球放入水中,结果水满并溢出。
根据以上过程,推测一个这样的玻璃球的体积范围是( )。
A.10cm 以上,15cm 以下 B.15cm 以上,20cm 以下
C.20cm 以上,25cm 以下 D.25cm 以上,30cm 以下
三、常见题型
6.求不规则物体的体积(容积)
C
7.判断。
(1)容积的计算方法和体积的计算方法相同,所以物体的体积就是物体的容积。 ( )
(2)圆柱形水桶的底面积越大,它的容积就越大。 ( )
三、常见题型
8.圆锥
三、常见题型
(1)一个圆锥形谷堆,底面直径为 6 m,高 1.2 m。求体积
3.14×(6÷2) ×1.2×1/3
=28.26×1.2×1/3
=11.304(立方米)
8.圆锥
三、常见题型
(2)把一块体积是150 cm3的圆柱形木材削成一个最大的圆锥,则削去部分的体积是( )cm3。
100
8.圆锥
三、常见题型
(3)一个圆锥形容器高6厘米,容器中装满水,如果将水全部倒入与它等底等高的圆柱形容器中,水高( )厘米。(容器的厚度忽略不计)
2
8.圆锥
三、常见题型
(4)将一个长15 cm,宽12 cm,高6 cm的长方体铁块锻造成一个底面积是90 cm 的圆锥,这个圆锥的高是多少厘米?
15×12×6×3÷90=36(cm)
(5)用一个两条直角边分别为8厘米、6厘米的直角三角形,以长直角边为轴旋转成圆锥,求圆锥的体积。
三、常见题型
8.圆锥
3.14×6 ×8×1/3
=113.04×8×1/3
=301.44(立方厘米)
长直角边为高h,短直角边为半径r
8.圆锥
三、常见题型
1)圆柱的体积等于圆锥体积的3倍。()
2)以三角形的一条边为轴旋转一周一定可以得到一个圆锥体。()
3)有一个顶点和一个底面的一定是圆锥 。 ()
(6)判断
空白演示
单击输入您的封面副标题
谢 谢 聆 听
整理复习第四单元
2022.4.6
一、圆柱
侧面积=底面周长×高=Ch=Πdh=2Πrh
表面积=侧面积+ 2×底面积
=Ch+2Πr =Πdh+2Πr =2Πrh+2Πr
区别
1.意义
2.测量数据
3.单位
体积=底面积×高=Πr h
容积=底面积×高=Πr h
相同点
计算公式
1.侧面积
2.表面积
3.体积、容积
二、圆锥
2.体积公式
1.特征:一个顶点
一个底面(圆)
一个侧面(曲面)
一个高
v=1/3底面积×高
圆锥的侧面展开是一个扇形。
三、常见题型
1.表面积的变化
(1)平行横截面切(切成几个小圆柱)
把一长为1.6分米的圆柱截成3段后,表面积增加了9.6平方米,求圆柱原来的体积?
9.6÷4×0.16
=2.4×0.16
=0.384(立方米)
切成3段,切了两下,切一下多两个底面积,所以四个底面积是9.6
三、常见题型
1.表面积的变化
(2)沿着直径向下切
把长为20分米的圆柱沿着底面直径劈开,表面积增加了80平方分米,求该圆柱原来的表面积是多少?
多的是两个长方形面积
长为d 宽为h(h=d时为正方形)
2dh=80
d=2
r=1
S=3.14×1×1×2+3.14×2×20
=131.88(平方分米)
三、常见题型
1.表面积的变化
(3)高的变化
一个圆柱的底面直径是10厘米,如果高增加2厘米,它的侧面积增加( )平方厘米.
A.31.4 B.62.8 C.157 D.20
B
表面积增加的是高为2 的圆柱的侧面积,体积增加的是高为2 的圆柱的体积。
三、常见题型
1.表面积的变化
(4)拼成近似长方体
一个圆柱拼成近似长方体表面积增加100,圆柱的半径是10,求圆柱的体积
增加的是两个长方形的面积(长为r,宽为h,当r=h时,是正方形)
2rh=100
h=5
V=3.14×10×10×5
三、常见题型
2.圆柱的展开图
(1)如何判断是圆柱的展开图?
2
6.28
2
4
15
4
3
3
3
3
4
4
A
B
C
三、常见题型
(2)展开图的应用
求圆柱的体积
由图得长方形得长为底面圆的周长C=Πd
Πd
d
d
2d+Πd=20.56
d=4
r=2
h=d=4
V=3.14×2×2×4
2.圆柱的展开图
一个圆柱的底面半径是2厘米,高是2厘米,如果沿高剪开,它的侧面展开图是( )形,这个图形的周长是( )厘米,面积是( )平方厘米。
(2)展开图的应用
周长为侧面展开图(长方形的周长),面积为长方形的面积,相当于圆柱的侧面积
长=底面周长C,宽为高h
周长=(C+h)×2
=(2×3.14×2+2)×2
=29.12
面积=Ch
=2×3.14×2×2
=25.12
2.圆柱的展开图
三、常见题型
(3)正方形侧面展开图
C=Πd=2Πr=h
1.一个圆柱的侧面展开图是一个正方形,这个圆柱的高与底面半径的比是( )。
A.2π∶1 B.1∶π C.π∶1 D.1∶2π
2.一张正方形的纸围成的圆柱,它的底面积和侧面积的比是( )。
A.π∶1 B.1∶π C.1∶4π D.4π∶1
A
C
三、常见题型
2.圆柱的展开图
3.实际应用
(1)压路机
压路机的前轮是圆柱形,它的宽是2米,前轮的底面半径是6分米,如果压路机的前轮每分钟转10周,那么它10分钟压路的面积是多少平方米?
753.6平方米
三、常见题型
3.实际应用
(2)压路机变形
如图所示,圆柱形石碾的底面直径和高都是1米。石碾从A墙滚动到B墙,它碾过的地面面积是多少平方米
4平方米
三、常见题型
3.实际应用
(3)彩带
用丝带捆扎一个圆柱形蛋糕盒(如图),打结用去20cm。捆扎这个蛋糕盒用去丝带多少厘米?
280厘米
三、常见题型
3.实际应用
(4)大棚
王伯伯要在一块地里搭建一个半圆柱形的蔬菜大棚(示意图如下),这块地长24米,宽5米,其中埋入地下部分的塑料薄膜的面积为35平方米,搭建这个蔬菜大棚至少要用多少平方米的塑料薄膜?(蔬菜大棚要将这块地完全覆盖)
243.025平方米
三、常见题型
4.长方形“变”圆柱
三、常见题型
(1)绕长旋转
长为高h,宽为半径r
4.长方形“变”圆柱
三、常见题型
(2)绕宽旋转
宽为高h,长为半径r
4.长方形“变”圆柱
三、常见题型
(3)以长为底面周长围成圆柱
宽为高h,长=底面周长
4.长方形“变”圆柱
三、常见题型
(4)以宽为底面周长围成圆柱
长为高h,宽=底面周长
三、常见题型
5.体积的变化
(1).半径扩大2倍,高不变,体积()
(2).底面积扩大2倍,高不变,体积()
(3).半径不变,高扩大2倍,体积()
(4).半径扩大3,高扩大2倍,体积()
体积=底面积×高=Πr h
6.求不规则物体的体积(容积)
(1)一个圆柱形鱼缸,如下图,把鱼缸中的鱼取出后,水面下降了2厘米,这条鱼的体积是多少?
r=25 2=12.5(厘米)
V=3.14×12.5×12.5×2
=981.25(立方厘米)
三、常见题型
(2)一个密封的瓶子里装着一些水,如图所示。已知瓶子的内底面积为15cm ,瓶子的容积是( )mL。
90
6.求不规则物体的体积(容积)
三、常见题型
(3)按下述步骤测量一颗玻璃球的体积:
①将400mL水倒入一个容积为500mL的烧杯中;
②将4颗相同的玻璃球放入水中,结果水还不满;
③再将1颗同样的玻璃球放入水中,结果水满并溢出。
根据以上过程,推测一个这样的玻璃球的体积范围是( )。
A.10cm 以上,15cm 以下 B.15cm 以上,20cm 以下
C.20cm 以上,25cm 以下 D.25cm 以上,30cm 以下
三、常见题型
6.求不规则物体的体积(容积)
C
7.判断。
(1)容积的计算方法和体积的计算方法相同,所以物体的体积就是物体的容积。 ( )
(2)圆柱形水桶的底面积越大,它的容积就越大。 ( )
三、常见题型
8.圆锥
三、常见题型
(1)一个圆锥形谷堆,底面直径为 6 m,高 1.2 m。求体积
3.14×(6÷2) ×1.2×1/3
=28.26×1.2×1/3
=11.304(立方米)
8.圆锥
三、常见题型
(2)把一块体积是150 cm3的圆柱形木材削成一个最大的圆锥,则削去部分的体积是( )cm3。
100
8.圆锥
三、常见题型
(3)一个圆锥形容器高6厘米,容器中装满水,如果将水全部倒入与它等底等高的圆柱形容器中,水高( )厘米。(容器的厚度忽略不计)
2
8.圆锥
三、常见题型
(4)将一个长15 cm,宽12 cm,高6 cm的长方体铁块锻造成一个底面积是90 cm 的圆锥,这个圆锥的高是多少厘米?
15×12×6×3÷90=36(cm)
(5)用一个两条直角边分别为8厘米、6厘米的直角三角形,以长直角边为轴旋转成圆锥,求圆锥的体积。
三、常见题型
8.圆锥
3.14×6 ×8×1/3
=113.04×8×1/3
=301.44(立方厘米)
长直角边为高h,短直角边为半径r
8.圆锥
三、常见题型
1)圆柱的体积等于圆锥体积的3倍。()
2)以三角形的一条边为轴旋转一周一定可以得到一个圆锥体。()
3)有一个顶点和一个底面的一定是圆锥 。 ()
(6)判断
空白演示
单击输入您的封面副标题
谢 谢 聆 听
