20023-2024学年第二学期甘肃省武威市凉州区七年级数学人教版第五章《相交线与平行线》单元测试卷(含答案)
文档属性
| 名称 | 20023-2024学年第二学期甘肃省武威市凉州区七年级数学人教版第五章《相交线与平行线》单元测试卷(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 406.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-28 16:49:22 | ||
图片预览



文档简介
20023-2024学年第二学期甘肃省武威市凉州区七年级数学第五章《相交线与平行线》单元测试卷
一、选择题(共10题;共30分)
1.(3分)如图所示的图案分别是三菱、大众、奥迪、奔驰汽车的车标,其中可以看成是由“基本图案”经过平移得到的是( )
A. B.
C. D.
2.(3分)如图,已知射线BA,BC被直线EF所截,图中的∠1与∠2是( )
A.对顶角 B.同位角 C.内错角 D.同旁内角
3.(3分)如图,直线与相交于点,若,则的度数为( )
A. B. C. D.
4.(3分)下列说法中正确的个数有( )
①从直线外一点到已知直线的垂线段叫做点到直线的距离;
②连接直线外一点与直线上各点的所有线段中,垂线段最短;
③,,三点在同一直线上且,则是线段的中点;
④在同一平面内,两条直线的位置关系有两种:平行与相交;
A.1个 B.2个 C.3个 D.4个
5.(3分)下列命题属于真命题的是( )
A.同旁内角相等,两直线平行
B.相等的角是对顶角
C.平行于同一条直线的两条直线平行
D.同位角相等
6.(3分)如图,点E在AD的延长线上,下列条件中能判断BC∥AD的是( )
A.∠1=∠2 B.∠A=∠5
C.∠A+∠ADC=180° D.∠3=∠4
7.(3分)将直角三角板和直尺如图放置、若,则的度数为( )
A. B. C. D.
8.(3分)如图,直线,相交于点,射线平分,.若,则的度数为( )
A. B. C. D.
9.(3分)如图,将 ABCD的一边BC延长至点E,若∠A=110°,则∠1等于( )
A.110° B.35° C.70° D.55°
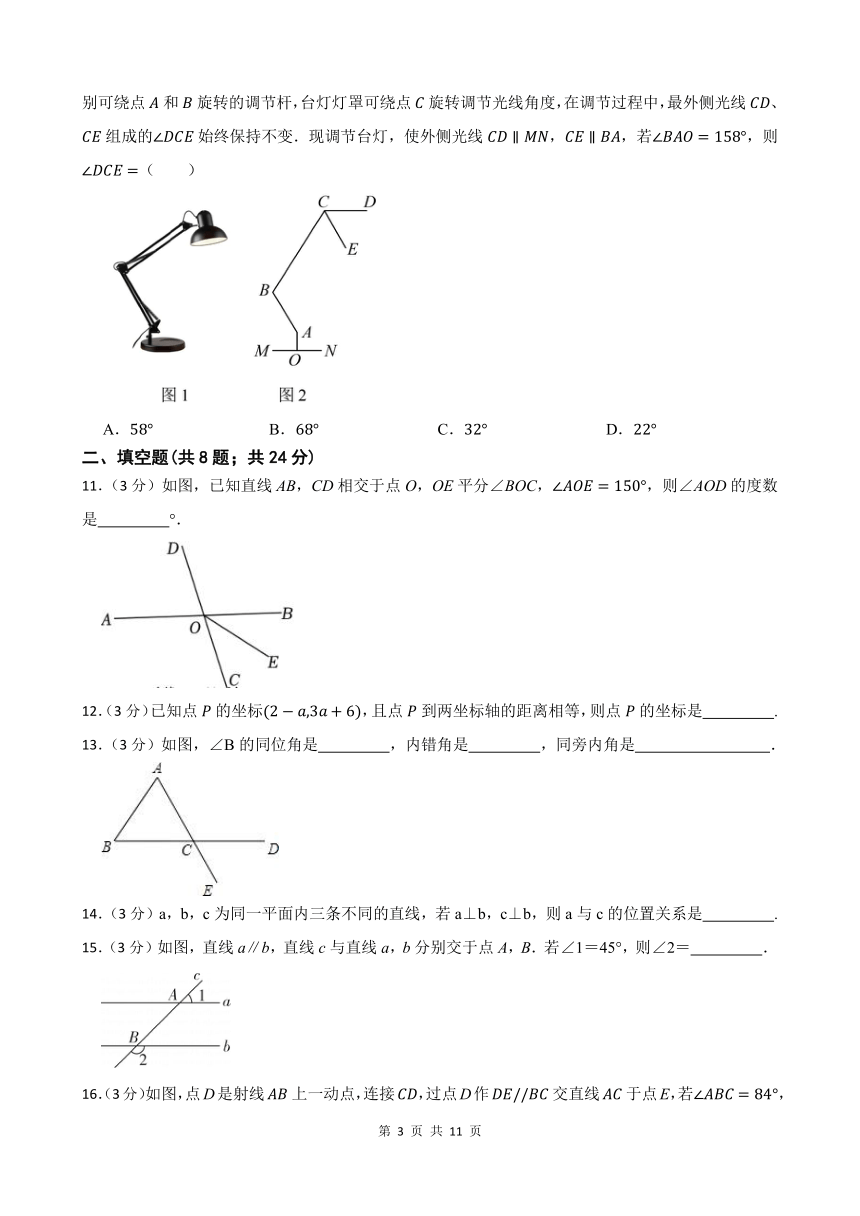
10.(3分)如图是一盏可调节台灯及其示意图.固定支撑杆垂直底座于点,与是分别可绕点和旋转的调节杆,台灯灯罩可绕点旋转调节光线角度,在调节过程中,最外侧光线、组成的始终保持不变.现调节台灯,使外侧光线,,若,则( )
A. B. C. D.
二、填空题(共8题;共24分)
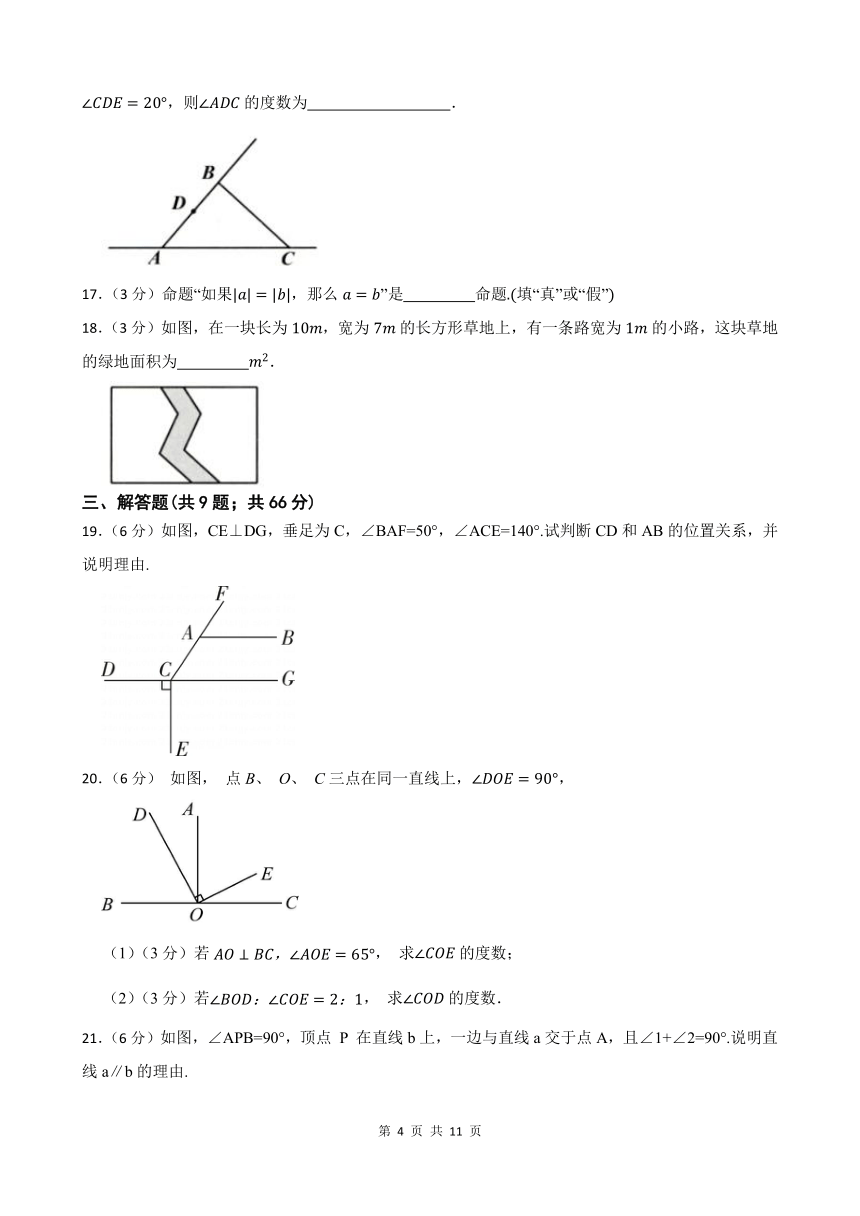
11.(3分)如图,已知直线AB,CD相交于点O,OE平分∠BOC,,则∠AOD的度数是 °.
12.(3分)已知点的坐标,且点到两坐标轴的距离相等,则点的坐标是 .
13.(3分)如图,∠B的同位角是 ,内错角是 ,同旁内角是 .
14.(3分)a,b,c为同一平面内三条不同的直线,若a⊥b,c⊥b,则a与c的位置关系是 .
15.(3分)如图,直线a∥b,直线c与直线a,b分别交于点A,B.若∠1=45°,则∠2= .
16.(3分)如图,点D是射线上一动点,连接,过点D作交直线于点E,若,,则的度数为 .
17.(3分)命题“如果,那么”是 命题填“真”或“假”
18.(3分)如图,在一块长为,宽为的长方形草地上,有一条路宽为的小路,这块草地的绿地面积为 .
三、解答题(共9题;共66分)
19.(6分)如图,CE⊥DG,垂足为C,∠BAF=50°,∠ACE=140°.试判断CD和AB的位置关系,并说明理由.
20.(6分) 如图, 点B、 O、 C三点在同一直线上,,
(1)(3分)若, 求的度数;
(2)(3分)若, 求的度数.
21.(6分)如图,∠APB=90°,顶点 P 在直线b上,一边与直线a交于点A,且∠1+∠2=90°.说明直线a∥b的理由.
22.(6分)如图,已知∠1=∠3,∠2+∠3=180°,则AB∥DE.完成下面的说理过程(填空).
解:将∠2的邻补角记作∠4,则
∠2+∠4= °( ).
又∵∠2+∠3=180°,
∴∠3=∠4( ).
又∵∠1=∠3,
∴ = (等量代换),
∴AB∥DE( ).
23.(8分)如图,直线AB,CD相交于点O,OD平分∠EOB,OF平分∠AOE,GH⊥CD,垂足为H,GH与FO平行吗?说明理由。
24.(8分)已知,,,平分.试说明平分.
25.(8分)如图,把一张长方形纸片ABCD沿EF折叠,点D,C分别落在D',C的位置上,ED'的延长线与BC交于点G.若∠EFG= 63°,求∠1,∠2的度数.
26.(8分)如图,平分.
(1)(4分)求证:.
(2)(4分)若,求的度数.
27.(10分)已知,的平分线与的平分线相交于点F.
(1)(3分)在图1中,求证:
①;
②;
(2)(3分)如图2,当,时,请你写出与之间的关系,并加以证明;
(3)(4分)当,,且时,请你直接写出的度数(用含m,n的式子表示)
答案
1.C
2.C
3.C
4.C
5.C
6.A
7.D
8.C
9.C
10.B
11.60
12.2800
13.∠ACD;∠BCE;∠BAC和∠ACB
14.a∥c
15.135°
16.或
17.假
18.63
19.解:CD∥AB,理由如下:
∵CE⊥DG,
∴∠ECG=90°,
又∵∠ACE=140°,
∴∠ACG=50°,
∵∠BAF=50°,
∴∠ACG=∠BAF,
∴AB∥CG,
即AB∥CD.
20.(1)解:∵即,,
∴,
∴的度数为.
(2)解:由题意知,
又∵,
∴,
∴,
∴的度数为.
21.证明:如图,
∵∠APB=∠2+∠3=90°,
∠1+∠2=90°,
∴∠1=∠3,
∴a∥b.
22.解:将∠2的邻补角记作∠4,则
∠2+∠4=180°(平角的定义).
又∵∠2+∠3=180°,
∴∠3=∠4(同角的补角相等).
又∵∠1=∠3,
∴∠1=∠4(等量代换),
∴AB∥DE(同位角相等,两直线平行).
故答案为:180;平角的定义;同角的补角相等;∠1,∠4;同位角相等,两直线平行.
23.解:GH∥FO,
理由如下:
∵OD平分∠EOB,∴∠DOE=
∵OF平分∠AOE,
,
∵GH⊥CD,
∴∠GHO=90°,
∴∠GHO=∠FOD
∴GH∥FO.
24.证明:∵(已知),
∴(两直线平行,同位角相等),
即,
∵(已知),
∴(两直线平行,内错角相等);
∵(已知),
∴(等量代换),
∴(等式性质);
∵平分(已知),
∴(角平分线的定义),
∴(等量代换),
∴平分(角平分线的定义).
25.解:∵AD∥BC,∴∠DEF=∠EFG=63°,由折叠知∠D'EF=∠DEF=63°,
∴∠1=180°-∠D'EF-∠DEF=54°.∵AD∥BC,∴∠1+∠2=180°,∴∠2=180°-∠1=
26.(1)解:,
平分.
.
,
.
(2)解:.
由(1)可知,.
27.(1)证明:①如图1,过点作
,
,
,
证明:②如图1,过点作
,
,
即;
(2)解:关系式为,
证明:设,
,时,且平分,平分,
,
由(1)得,
,
,
,
即,
,
(3)解:设则
,,
由(1)可得
,
,
,
,
,
即的度数(用含m,n的式子表示)表示为
一、选择题(共10题;共30分)
1.(3分)如图所示的图案分别是三菱、大众、奥迪、奔驰汽车的车标,其中可以看成是由“基本图案”经过平移得到的是( )
A. B.
C. D.
2.(3分)如图,已知射线BA,BC被直线EF所截,图中的∠1与∠2是( )
A.对顶角 B.同位角 C.内错角 D.同旁内角
3.(3分)如图,直线与相交于点,若,则的度数为( )
A. B. C. D.
4.(3分)下列说法中正确的个数有( )
①从直线外一点到已知直线的垂线段叫做点到直线的距离;
②连接直线外一点与直线上各点的所有线段中,垂线段最短;
③,,三点在同一直线上且,则是线段的中点;
④在同一平面内,两条直线的位置关系有两种:平行与相交;
A.1个 B.2个 C.3个 D.4个
5.(3分)下列命题属于真命题的是( )
A.同旁内角相等,两直线平行
B.相等的角是对顶角
C.平行于同一条直线的两条直线平行
D.同位角相等
6.(3分)如图,点E在AD的延长线上,下列条件中能判断BC∥AD的是( )
A.∠1=∠2 B.∠A=∠5
C.∠A+∠ADC=180° D.∠3=∠4
7.(3分)将直角三角板和直尺如图放置、若,则的度数为( )
A. B. C. D.
8.(3分)如图,直线,相交于点,射线平分,.若,则的度数为( )
A. B. C. D.
9.(3分)如图,将 ABCD的一边BC延长至点E,若∠A=110°,则∠1等于( )
A.110° B.35° C.70° D.55°
10.(3分)如图是一盏可调节台灯及其示意图.固定支撑杆垂直底座于点,与是分别可绕点和旋转的调节杆,台灯灯罩可绕点旋转调节光线角度,在调节过程中,最外侧光线、组成的始终保持不变.现调节台灯,使外侧光线,,若,则( )
A. B. C. D.
二、填空题(共8题;共24分)
11.(3分)如图,已知直线AB,CD相交于点O,OE平分∠BOC,,则∠AOD的度数是 °.
12.(3分)已知点的坐标,且点到两坐标轴的距离相等,则点的坐标是 .
13.(3分)如图,∠B的同位角是 ,内错角是 ,同旁内角是 .
14.(3分)a,b,c为同一平面内三条不同的直线,若a⊥b,c⊥b,则a与c的位置关系是 .
15.(3分)如图,直线a∥b,直线c与直线a,b分别交于点A,B.若∠1=45°,则∠2= .
16.(3分)如图,点D是射线上一动点,连接,过点D作交直线于点E,若,,则的度数为 .
17.(3分)命题“如果,那么”是 命题填“真”或“假”
18.(3分)如图,在一块长为,宽为的长方形草地上,有一条路宽为的小路,这块草地的绿地面积为 .
三、解答题(共9题;共66分)
19.(6分)如图,CE⊥DG,垂足为C,∠BAF=50°,∠ACE=140°.试判断CD和AB的位置关系,并说明理由.
20.(6分) 如图, 点B、 O、 C三点在同一直线上,,
(1)(3分)若, 求的度数;
(2)(3分)若, 求的度数.
21.(6分)如图,∠APB=90°,顶点 P 在直线b上,一边与直线a交于点A,且∠1+∠2=90°.说明直线a∥b的理由.
22.(6分)如图,已知∠1=∠3,∠2+∠3=180°,则AB∥DE.完成下面的说理过程(填空).
解:将∠2的邻补角记作∠4,则
∠2+∠4= °( ).
又∵∠2+∠3=180°,
∴∠3=∠4( ).
又∵∠1=∠3,
∴ = (等量代换),
∴AB∥DE( ).
23.(8分)如图,直线AB,CD相交于点O,OD平分∠EOB,OF平分∠AOE,GH⊥CD,垂足为H,GH与FO平行吗?说明理由。
24.(8分)已知,,,平分.试说明平分.
25.(8分)如图,把一张长方形纸片ABCD沿EF折叠,点D,C分别落在D',C的位置上,ED'的延长线与BC交于点G.若∠EFG= 63°,求∠1,∠2的度数.
26.(8分)如图,平分.
(1)(4分)求证:.
(2)(4分)若,求的度数.
27.(10分)已知,的平分线与的平分线相交于点F.
(1)(3分)在图1中,求证:
①;
②;
(2)(3分)如图2,当,时,请你写出与之间的关系,并加以证明;
(3)(4分)当,,且时,请你直接写出的度数(用含m,n的式子表示)
答案
1.C
2.C
3.C
4.C
5.C
6.A
7.D
8.C
9.C
10.B
11.60
12.2800
13.∠ACD;∠BCE;∠BAC和∠ACB
14.a∥c
15.135°
16.或
17.假
18.63
19.解:CD∥AB,理由如下:
∵CE⊥DG,
∴∠ECG=90°,
又∵∠ACE=140°,
∴∠ACG=50°,
∵∠BAF=50°,
∴∠ACG=∠BAF,
∴AB∥CG,
即AB∥CD.
20.(1)解:∵即,,
∴,
∴的度数为.
(2)解:由题意知,
又∵,
∴,
∴,
∴的度数为.
21.证明:如图,
∵∠APB=∠2+∠3=90°,
∠1+∠2=90°,
∴∠1=∠3,
∴a∥b.
22.解:将∠2的邻补角记作∠4,则
∠2+∠4=180°(平角的定义).
又∵∠2+∠3=180°,
∴∠3=∠4(同角的补角相等).
又∵∠1=∠3,
∴∠1=∠4(等量代换),
∴AB∥DE(同位角相等,两直线平行).
故答案为:180;平角的定义;同角的补角相等;∠1,∠4;同位角相等,两直线平行.
23.解:GH∥FO,
理由如下:
∵OD平分∠EOB,∴∠DOE=
∵OF平分∠AOE,
,
∵GH⊥CD,
∴∠GHO=90°,
∴∠GHO=∠FOD
∴GH∥FO.
24.证明:∵(已知),
∴(两直线平行,同位角相等),
即,
∵(已知),
∴(两直线平行,内错角相等);
∵(已知),
∴(等量代换),
∴(等式性质);
∵平分(已知),
∴(角平分线的定义),
∴(等量代换),
∴平分(角平分线的定义).
25.解:∵AD∥BC,∴∠DEF=∠EFG=63°,由折叠知∠D'EF=∠DEF=63°,
∴∠1=180°-∠D'EF-∠DEF=54°.∵AD∥BC,∴∠1+∠2=180°,∴∠2=180°-∠1=
26.(1)解:,
平分.
.
,
.
(2)解:.
由(1)可知,.
27.(1)证明:①如图1,过点作
,
,
,
证明:②如图1,过点作
,
,
即;
(2)解:关系式为,
证明:设,
,时,且平分,平分,
,
由(1)得,
,
,
,
即,
,
(3)解:设则
,,
由(1)可得
,
,
,
,
,
即的度数(用含m,n的式子表示)表示为
